脉冲噪声环境下基于矩阵差分的远近场混合源定位
母采凤 李 森 吕梦然
(大连海事大学信息科学技术学院,辽宁大连 116026)
1 引言
信号源定位在雷达信号处理、射电天文学、地质学、海洋学中具有广泛的应用[1],依据信号源与接收阵列之间的距离,信号源可以分为远场源信号和近场源信号。在远场源定位场景中,入射源假设为平面波,信号源定位仅需要对方位角进行估计;在近场源定位场景中,入射源被认为是球面波而不是平面波,因此近场源定位需要对方位角和距离进行联合估计。在现实生活的某些场景中既存在远场信号源也存在近场信号源,如基于麦克风阵列的语音信号定位,此时的信号源称为远近场混合源。近年来远近场混合源定位问题受到研究者们的广泛关注[2-10]。
远近场混合源定位主要包括远近场分离和定位参数估计两个问题。对于远近场分离,诸多算法被提出。其中,基于斜投影的远近场分离算法[2-3]是在首先估计出远场源的方位角的基础上构造斜投影矩阵,然后在阵列观测数据中利用斜投影技术去除远场观测数据获得近场观测数据。斜投影分离算法会造成阵列孔径损失,使得定位精度下降。基于子空间差分[4-5]的远近场分离算法是在首先估计出远场源的方位角和信号功率的基础上重构远场源协方差矩阵,然后从远近场混合源协方差矩阵中减去远场源协方差矩阵得到近场源协方差矩阵。这种分离方法可以避免阵列孔径损失,但是远场源方位角定位精度会对分离后得到的近场源协方差矩阵产生很大的影响,从而影响近场源定位精度。基于矩阵差分的远近场分离算法[6]利用远近场源各自协方差矩阵具有不同的结构特性实现远近场分离,相较于基于子空间差分的分离算法,这种分离方法得到的近场源协方差分量不受远场方位角估计精度的影响能获得更为纯净的近场分量,实现了更为理想的远近场源分离。文献[7]将矩阵差分法和子空间差分法结合起来,提出了一种基于两步差分法的(TS-MD)远近场混合源定位算法。在TS-MD算法中首先采用矩阵差分技术得到纯净的近场源分量,在估计得到近场源参数的基础上构造近场源协方差矩阵,然后采用子空间差分技术从远近场混合源协方差矩阵中得到纯净的远场源协方差矩阵,从而避免了由近场源等效为虚拟远场源引起的伪峰问题。但是近场源定位参数的估计精度会影响子空间差分后得到的远场源协方差矩阵的精度,进而影响到远场源方位角的估计精度。
在远近场分离后可分别对远场信号源和近场信号源的定位参数进行估计。定位参数估计方法主要分为两大类:基于子空间的估计算法和基于稀疏重构的估计算法。基于子空间的估计算法已经非常成熟,主要有多重信号分类方法(multiple sig⁃nal classification,MUSIC)[11]和基于旋转不变技术的估计算法(estimating signal parameter via rotational invariance techniques,ESPRIT)[12]。例如文献[4]中采用MUSIC 算法分别实现对远场源方位角和近场源距离的估计,而采用类ESPRIT 算法实现对近场源方位角的估计。近几年,基于稀疏重构的远近场混合源定位算法也得到广泛研究。文献[8]在远场源和近场源参数估计中分别用稀疏重构算法代替子空间算法,有效避免了谱峰搜索且得到了更好的估计性能。文献[9]利用高阶累积量和无网格稀疏重构算法研究了基于交叉阵列的远近场混合源定位问题,避免网格失配和阵列孔径的损失。
在现实环境中,自然现象或人为因素的影响使得噪声具有突发、短时、高振幅的特性,这类噪声的概率密度函数比高斯分布噪声的概率密度函数拖尾更加厚重。对称α-稳定分布(symmetric α-stable distribution,SαS)被广泛用于描述这类噪声,其特征指数α影响SαS 分布的拖尾厚度,α越小意味着SαS分布的拖尾越厚,噪声脉冲性越强;反之,意味着SαS 分布的拖尾越薄,噪声脉冲性越弱。当α=2时,SαS 分布为高斯分布,当0 <α<2 时,SαS 分布只有阶数小于α的矩才是有界的,在SαS 分布噪声环境下基于二阶和高阶统计量的信号处理算法的性能会退化甚至失效。针对这一问题,分数低阶统计量[13],非线性变换预处理[14]、相关熵[15]等方法成为脉冲噪声环境下信号处理的重要工具。现有文献中关于脉冲噪声环境下的DOA 估计算法大多数针对单独的远场源或近场源[16-17],对于脉冲噪声环境下的远近场混合源定位问题研究较少,仅文献[18]对此问题进行了研究。在文献[18]中首先构造了仅包含远近场源方位角信息的协方差向量稀疏表示模型,并在稀疏重建代价函数中通过引入相关熵来抑制脉冲噪声,然后在基于Root-MUSIC算法的距离估计中采用非线性变换预处理的方法来抑制脉冲噪声。文献[18]中并没有实现远近场的分离,而是通过估计得到的距离值大小来实现远近场信源识别的。本文受矩阵差分算法的启发,首先利用分数低阶协方差矩阵差分(FLOC-MD)和压缩变换协方差矩阵差分(CTC-MD)的分离算法实现远近场混合源的分离,然后分别利用子空间算法实现定位参数的估计。仿真结果表明,本文所提算法能有效抑制脉冲噪声的干扰,相比于传统的基于二阶协方差矩阵差分(COV-MD)的远近场混合源定位算法能够获得更为精确的估计,且CTC-MD 算法明显优于FLOC-MD算法并且不依赖于脉冲噪声的先验信息。
2 系统模型
如图1 所示是一个阵元数为L=2N+1 的均匀线阵,混合源信号为M个相互独立的信号,包含M1个近场信号和M-M1个远场信号,以第N+1 个阵元为参考阵元建立直角坐标。

图1 均匀线阵模型Fig.1 Uniform linear array model
第l个阵元在t时刻的接收信号可以表示为


3 改进的鲁棒协方差矩阵
3.1 分数低阶协方差矩阵
当SαS 噪声的特征指数α<2 时,基于协方差矩阵的定位参数估计算法性能将退化甚至失效,此时可以用分数低阶协方差来代替协方差,阵列接收信号的分数低阶协方差矩阵定义为[16-17]

3.2 压缩变换协方差矩阵
文献[14]提出了一种非线性压缩变换函数,该函数定义为

其中,σ为尺度变换参数它的取值不依赖于噪声的特征指数α。可以证明在SαS 噪声中的信号经过非线性压缩变换后具有有限的二阶统计量[14]。因此定义阵列接收信号的压缩变换协方差矩阵为

将RFLOC和RCT统一表示为Rζ,由于噪声与信号是相互独立的,则其可以表示为

性质1:满足Toeplitz结构。
证明:以远场阵列接收信号的分数低阶协方差矩阵为例,由于源信号之间是相互独立的,则其第(k,q)个元素和第(k+1,q+1)个元素分别为:


同理可证远场阵列接收信号的分数低阶协方差矩阵对角线上的元素满足:

结合公式(11)可知远场分数低阶协方差矩阵满足Toeplitz结构。
同理可证远场压缩变换协方差矩阵也满足To⁃eplitz 结构,因此有,其中为反方向单位矩阵。
性质2:满足Hermitian结构,即
证明:以近场阵列接收信号的分数低阶协方差矩阵为例,其第(k,q)和(q,k)个元素为


4 定位参数估计
4.1 远场源方位角参数估计

4.2 近场源方位角参数估计
由性质1 和2 可得仅包含近场信息的扩展矩阵:


4.3 近场源距离参数估计
将得到的近场方位角估计值代入近场导向矢量,再次通过一维MUSIC 谱峰搜索可以得到与角度对应的近场距离。
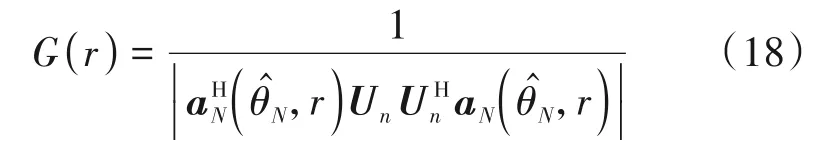
5 仿真结果与分析
为了验证算法的有效性,将本文提出的两种算法与基于二阶统计量的COV-MD 算法和TS-MD 算法进行比较。在以下仿真实验中,对称均匀线阵由11 个阵元构成,阵元间隔d=λ4,共有M=4 个信号源,M1=2 个近场信号源和两个远场信号源。远场源的方位角分别为θ1=-20°和θ2=30°,近场源的方位角和距离分别为(θ3,r3)=(-10°,1.8λ)和(θ4,r4)=(20°,1.2λ)。背景噪声为加性SαS 噪声,由于其不存在有限的二阶矩,噪声的方差没有意义,因此本文采用广义信噪比(generation signal of noise ratio,GSNR),GSNR=。
采用均方根误差(root mean square error,RMSE)作为算法的性能指标,定义为:

其中K=M1或K=M-M1,Ne为蒙特卡罗仿真实验次数,本文所有实验中的Ne均为500次,pk为方位角或距离的真实值是pk第ne次仿真实验的估计值。
实验1不同广义信噪比下性能分析
给定特征指数和快拍数分别为1.6和500,GSNR从2 dB 变化到20 dB。TS-MD,COV-MD,FLOC-MD和CTC-MD四种算法的性能随广义信噪比的变化曲线如图2所示。可以看出对于远近场定位参数估计,四种算法的均方根误差都随信噪比的增大合理地减小。由于在SαS噪声条件下二阶统计量不存在,因而TS-MD 算法和COV-MD 算法的估计性能都要低于FLOC-MD和CTC-MD算法。对于近场源方位角和距离的估计,由于TS-MD 算法和COV-MD 算法的估计方法完全一致,所以两种算法的性能几乎相同。对于远场源方位角的估计,虽然TS-MD算法避免了COVMD 算法中由近场源等效为虚拟远场源引起的伪峰问题,但是由于受到近场源定位参数估计精度的影响,TS-MD 算法的估计性能并没有优于COV-MD 算法。本文提出的两种算法在低信噪比情况下的估计性能要明显优于COV-MD 算法和TS-MD 算法,且CTC-MD算法的性能要优于FLOC-MD算法。
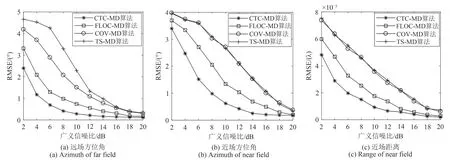
图2 算法性能随广义信噪比变化曲线Fig.2 Curve of algorithm performance with GSNR
实验2不同特征指数下性能分析
给定GSNR 和快拍数分别为16 dB 和500,特征指数从1.0 变化到1.9,图3 给出了四种算法的性能随着特征指数变化的曲线。从图中可以看出随着特征指数增加即随着噪声脉冲性减弱,四种算法定位参数估计的均方根误差在逐渐减小。在同一特征指数的脉冲噪声条件下,特别是在强脉冲噪声环境下本文所提出的两种算法性能明显优于TS-MD算法和COV-MD 算法,且CTC-MD 算法的估计性能优于FLOC-MD算法。
图3 算法性能随特征指数变化曲线Fig.3 Curve of algorithm performance with characteristic index
实验3不同快拍数下性能分析
给定GSNR 和脉冲噪声的特征指数分别为16 dB 和1.6,快拍数从300变化到1500,图4中给出了算法性能随快拍数变化的曲线。从图中可以看到四种算法的均方根误差都随着快拍数的增加在逐渐减小。同样地,在同一快拍数条件下,本文所提得两种算法性能明显优于TS-MD 算法和COV-MD 算法,CTC-MD算法的估计性能优于FLOC-MD算法。

图4 算法性能随快拍数变化曲线Fig.4 Curve of algorithm performance with the number of snapshots
6 结论
本文提出了脉冲噪声条件下两种远近场混合源定位参数的估计算法,基于分数低阶协方差的矩阵差分算法和基于压缩变换协方差的矩阵差分算法。相较于传统的基于二阶统计量的矩阵差分算法和两步差分算法,本文所提的这两种算法均能抑制脉冲噪声的干扰,有效提高了定位估计的精度。且基于压缩变换协方差的矩阵差分算法不仅估计性能要好于基于分数低阶协方差的矩阵差分算法而且算法的应用不依赖于脉冲噪声的先验信息。

