GBAS与ILS联合导航系统数据融合方法与验证
倪育德 张振楠 刘瑞华 秦 哲 王 凯 于颖丽
(1.中国民航大学电子信息与自动化学院,天津 300300;2.中国民航大学中欧航空工程师学院,天津 300300)
1 引言
电离层与多径分别是影响陆基增强系统(ground-based augmentation systems,GBAS)和仪表着陆系统(instrument landing systems,ILS)所需导航性能(required navigation performance,RNP)的两个主要误差源,但它们对这两个精密进近系统的RNP影响不同。GBAS 信号脆弱,易受电离层影响,当遭遇较强干扰如电离层风暴时,会导致机载GBAS 系统与GBAS基准站之间电离层延迟出现时间和空间去相关[1],但GBAS 针对检测、抑制和消除多径干扰采取了各种措施,多径效应对GBAS的影响较ILS的小。相反,由于ILS 工作体制设计的缺陷,导致其对场地敏感[2],但电离层风暴对ILS 的影响较GBAS 的小。因此,如果能够利用数据融合方法实现GBAS和ILS 的联合共用,就有可能提升联合导航系统的整体性能,提高精密进近运行的生存能力。
虽然目前导航系统的运行模式是机载飞行管理系统依据RNP 来选择相应导航源,但导航源进行融合以获得增强的RNP 是导航系统运行模式的一个发展方向。
国内外目前对导航源融合的研究主要集中在全球导航卫星系统(global navigation satellite sys⁃tem,GNSS)与惯性导航系统(inertial navigation sys⁃tem,INS)的组合[3-9],对GBAS 与ILS 数据融合研究的公开报道还很少见到。
2016 年,沈阳航空航天大学信息与通信工程系的宗平,利用飞机的试飞验证数据对差分GNSS 和ILS 数据融合进行了研究,提出了星基-仪表着陆系统组合进场策略,并基于卡尔曼滤波和扩展自适应融合算法实现了差分GNSS和ILS的数据融合。研究表明,在进近着陆过程中,利用该进场策略能有效提升导航性能,保证飞机安全进近着陆[10]。2018年,沈阳航空航天大学电子与通信工程系的于泠洁,利用飞机的试飞验证数据,对GBAS、ILS以及INS的数据融合进行了研究,该研究对比了扩展卡尔曼滤波(extended Kalman filter,EKF)、无迹卡尔曼滤波(un⁃scented Kalman filter,UKF)和容积卡尔曼滤波(cu⁃bature Kalman filter,CKF)的性能,提出了基于改进联邦无迹卡尔曼滤波的GBAS、ILS 和INS 导航系统融合算法,结果显示,该算法可提高导航的水平精度[11]。除此之外,还没有发现国内外对GBAS和ILS数据融合研究的其他公开报道。
本文基于目前的GBAS 提供I 类(category I,CAT I)的“类ILS”精密进近服务,只针对GBAS 与ILS 联合导航系统的RNP 最底层指标即精度进行研究。
在实现GBAS 与ILS 时间对准和空间对准基础上,分析了电离层风暴对GBAS 的影响及多径效应对ILS 的影响,基于局部坐标系建立了飞机精密进近运动模型,引入一种基于Sage-Husa 自适应滤波和方差估计学习算法的GBAS与ILS数据融合方法,实现了二者联合共用,使得GBAS与ILS分别在电离层风暴和多径干扰下,联合导航系统仍能提供满足CAT I精度要求的引导信息。
2 电离层风暴和多径效应对GBAS 和ILS的影响
2.1 电离层风暴对GBAS的影响
等离子体云伴随着太阳耀斑爆发而产生,等离子体云到达地球附近,与地球磁场作用引起磁暴。磁暴会引起全球范围的电离层发生剧烈变化,这种现象称为电离层风暴[12]。电离层风暴可用图1所示的移动楔形模型表示,该模型有斜坡梯度g、斜坡宽度w、电离层延迟变化幅度D和移动速度v四个关键参数[13]。

图1 电离层风暴移动楔形模型Fig.1 Ionospheric storm moving wedge model
表1给出了斜坡梯度上限与移动速度的关系,g的上限取决于移动速度,w的范围为25~200 km,D的最大值为50 m,三者关系为

表1 斜坡梯度上限与移动速度的关系Tab.1 Relationship between the upper bound on gradient slope and the propagation speed

飞机进近着陆过程中,电离层风暴对GBAS 定位的影响如图2 所示。图2 中vI为移动楔形模型移动速度,vP为飞机速度,其他参数含义与前面相同。电离层风暴会对GBAS 产生两种不良影响,一种是由电离层风暴迅速推进导致的电离层延迟在时间上的去相关,即在GBAS 基准站播发伪距差分改正数和完好性信息等的更新间隔内,电离层延迟发生突变;另一种是由电离层风暴梯度引起的飞机和GBAS 基准站之间的电离层延迟不同,即空间上的去相关[14]。由此导致较大的定位误差,使得GBAS无法为飞机提供满足CAT I精密进近精度要求的水平和垂直引导。

图2 电离层风暴对GBAS定位的影响Fig.2 Impact of ionospheric storm on GBAS positioning
2.2 多径效应对ILS的影响
对于ILS 的航向信标(localizer,LOC),由于机场跑道周围存在各种障碍物,机载接收机不仅会收到LOC辐射的直达信号,还会收到障碍物造成的反射信号(如图3 所示),使飞机在进近过程中的调制度差(difference in depth of modulation,DDM)出现扰动。

图3 LOC多径干扰Fig.3 Multipath interference on the LOC
直达的载波边带(carrier side band,CSB)信号和边带(side band only,SBO)信号分别为

式中,Ec是载波信号的幅值;Ω是基准角频率,其线性频率为30 Hz;m150和m90是调制度,取值均为0.2;ω为载波角频率;k是SBO信号相对于CSB信号的幅度;fCSB(θ)、fSBO(θ)分别为辐射CSB 信号和SBO 信号的方向性函数;θ为飞机偏离跑道中心线的角度。
假设仅有一条多径信号,障碍物与LOC 的连线跟跑道中心线的夹角为β,障碍物和机载接收机与LOC 的距离分别为dR1和dD,障碍物与机载接收机的距离为dR2,则反射信号相对于直达信号的延时为

式中,c=3×108m/s。
则机载接收机实际接收的信号为

同样,对于ILS 的下滑信标(glide slope,GS),若GS 台附近的地面不是水平的,则机载GS 将会受到多径干扰的影响,此时有[2]

式中,k是SBO 信号相对于CSB 信号的幅度,m为150 Hz和90 Hz信号的调制度,θ为飞机相对跑道的夹角,θFSL表示斜坡角,θ0为标称值3°的下滑角。
3 GBAS与ILS数据融合
3.1 飞机进近运动模型的建立
不考虑进场和复飞航段,一个仪表进近程序由起始进近航段、中间进近航段和最后进近航段组成[2],如图4所示,其中IAF、IF和FAF分别表示起始进近定位点、中间进近定位点和最后进近定位点,而MAPt是复飞点。

图4 飞机进近着陆过程Fig.4 Aircraft approach and landing process
在进近的某一航段,飞机的运动可等效为单一运动状态,而整个进近过程则是多航段多运动状态的组合。考虑到起始进近和最后进近运动状态相同,所以仅对中间进近和最后进近建立飞机进近运动模型。
以机场局部坐标系为基准坐标系。该坐标系以跑道入口点(landing threshold point,LTP)为原点,以GBAS 方位基准点(GBAS azimuth reference point,GARP)沿跑道中心线指向LTP 的方向为x轴正方向,以垂直于跑道平面且通过LTP 竖直向上的方向为z轴正方向,y轴垂直于xoz平面且满足右手定则。
在中间进近和最后进近阶段,飞机在x、y方向始终保持匀变加速运动;而z方向的运动状态相对复杂,在中间进近阶段,飞机高度基本不变,即飞机以很小的初速度进行匀速运动,当飞机从中间进近向最后进近过渡时,其运动状态可看做是匀变速运动,过渡阶段的时间比较短暂,在最后进近航段,飞机则一直保持匀速运动。
民航考虑到飞行安全问题,在飞机的进近过程中,要求飞行员必须严格按照仪表进近航图及飞行手册驾驶飞机,保证飞机平稳进近,不允许飞机出现强机动情况。因此,民航飞机在进近过程的运动状态存在一定的规律性,即主要为匀速、匀变速和匀变加速运动的组合。基于该背景,通过深入解析从模拟飞行软件X-Plane 中采集的多次进近着陆飞行数据,建立飞机从中间进近航段向最后进近航段过渡时的运动模型如下

飞机在中间进近航段和最后进近航段的运动模型为

3.2 联合导航系统数据融合的实现
传统的卡尔曼滤波针对状态方程和观测方程均为线性方程且状态噪声和观测噪声特性不变的场景。而在实际应用中,状态方程和观测方程通常为非线性方程,传统的卡尔曼滤波不适用于这种情况,相关研究人员在传统卡尔曼滤波的基础上,提出了EKF、UKF 及CKF 等算法以解决非线性问题。上述算法均以状态噪声和观测噪声特性不变为前提,当噪声特性改变时,滤波效果会受到影响,这时则需要采用自适应滤波算法。相关法是一种较为常见的自适应滤波算法,但其计算过程复杂,实时性较差,难以满足实际工程需要。
Sage-Husa 自适应滤波是在卡尔曼滤波基础上改进的一种自适应滤波算法,它是一种基于观测量噪声统计的极大后验(maximum a posteriori,MAP)估计器。该算法可利用观测数据,同时进行递推滤波和估计修正噪声统计特性,从而降低模型参数误差带来的影响,提高滤波精度,抑制发散[15]。飞机进近着陆过程的状态方程和观测方程均为线性方程,电离层风暴和多径效应持续变化,即观测噪声方差阵R不断改变。综上所述,Sage-Husa自适应滤波相较于其他算法更适用于该场景。
但Sage-Husa 自适应滤波无法在状态噪声方差阵Q和观测噪声方差阵R均未知的情况下同时对二者进行估计[16],而在Q给定情况下,可利用简化的Sage-Husa自适应滤波算法对R进行估计,过程如下

式中,b为遗忘因子(0 Sage-Husa 自适应滤波也存在一定问题。一方面,随着递推次数增加,新近观测数据的权重逐渐减少;另一方面,Sage-Husa 自适应滤波在对噪声方差估计时采用了减法运算,这会使噪声方差极易失去半正定性和正定性而导致滤波器发散,引入收敛判据和对dk的约束条件即可解决上述问题。 标量形式的收敛判据和对dk的约束条件为 式中,ε(k)为新息,H为观测矩阵,P(k|k−1)为一步预测协方差为k−1 时刻观测噪声方差阵估计值。 受干扰信息经过Sage-Husa 自适应滤波处理后,得到飞机的估计位置P1,同时未受干扰信息经空间对准算法处理得到飞机位置P2,再利用方差估计学习融合算法对其处理[17],过程如下 其中,w(ik)为加权因子,(k)为方差估计,(k)为数据方差。 GBAS 与ILS 联合系统的实现流程如图5 所示。有两点需要说明,其一,实现两个精密进近系统数据融合的前提是实现二者的时空对准,限于篇幅,本文不对该内容展开阐述,可参阅文献[18];其二,仿真数据源自美国Laminar Research 公司开发的商用模拟飞行软件X-Plane。该软件采用了与传统飞行模拟器不同的叶素理论,飞行数据精度很高,飞行效果极其逼真,已被国内外许多公司、政府部门或高校采购用作飞行员指定飞行模拟器或科学研究[19-23]。但目前X-Plane 内置的数据采集系统仅能输出有限类通用数据,无法输出本文所需的专业性很强的非通用数据,为此自行开发了图5 中的数据采集模块。 图5 GBAS与ILS数据融合流程Fig.5 GBAS and ILS data fusion process 虽然反映运输航空飞行状况的实际数据主要来自快速存储记录器(quick access recorder,QAR)[24],但QAR 数据精度较低,主要用于飞机性能评估、故障监测和事故调查等,不适合用作本文的数据源。 GBAS 与ILS数据融合整体过程如下:利用自行开发的数据采集模块从X-Plane 中获取飞行数据[25],并向数据添加电离层风暴或多径效应干扰,受干扰的GBAS或ILS信息时空对准后输入,经时间更新并计算ε,判断是否满足收敛条件,若满足则进一步计算dk,之后判断是否满足约束条件,若满足则更新R,否则不更新,经历观测更新的信息与时空对准后的未受干扰的ILS或GBAS信息经方差估计、权重计算和加权融合,最终输出融合后信息。 这部分将通过仿真实验,验证所给GBAS 和ILS 数据融合算法对GBAS/ILS 联合系统位置精度的影响。分以下3 种情况展开仿真实验:1)GBAS不受电离层风暴的影响,ILS 受弱多径效应影响(以下简称“正常情况”)(4.1 节);2)GBAS 受电离层风暴的影响,ILS 受弱多径效应影响(4.2 节);3)GBAS不受电离层风暴的影响,ILS 受多径效应影响(4.3节)。 (1)仿真条件设置 仿真采用从X-Plane 采集的飞行数据。由于XPlane的限制,若想采集按照标准进近程序完成进近着陆的飞行数据,必须执行从冷舱启动到安全着陆的完整飞行过程。 根据目前GBAS在机场的安装情况,起飞机场和目的机场分别设为澳门国际机场和上海浦东国际机场,航路点依次为SHL、G471、PLT、A599、ELNEX、G204、UGAGO、W507、DSH、W505、SUPAR、B221 以及AND,离场跑道和进场跑道分别为16 和34L,离场程序和进场程序分别为SHL9D 和AND15A,进场点为IGLT1。飞机从冷舱启动到安全着陆,X-Plane的整个运行过程需4小时左右,限于时间,共进行了4次飞行。 GBAS/ILS 关键点以及GBAS 地面基准站的坐标如表2 所示,其中LTP/FTP 为着陆入口点/虚拟入口点,GERP为GBAS高程基准点,FPAP为飞行路径对准点,GARP 为GBAS 方位基准点,DME 为测距机,RS表示GBAS地面基准站(共4个)。 表2 GBAS/ILS关键点和GBAS地面基准站位置Tab.2 GBAS/ILS key points and GBAS ground reference station location GBAS 不受电离层风暴的影响,ILS 受弱多径效应影响,对应β为36.25°且θFSL为0.065°的情况。利用3.2 节的数据融合算法对其处理。遗忘因子b取0.99,根据飞行数据计算飞机4次飞行的初始状态如表3所示,状态噪声方差阵Q=diag(10-14,10-14,10-7),观测噪声方差阵初始值R0=diag(0.0225,2.56,12.25)。 表3 飞行初始状态值(4次飞行)Tab.3 Initial flight state value(four flights) (2)仿真结果及分析 表4 为正常情况下,单独的GBAS 以及GBAS/ILS 联合系统这4 次飞行的数据统计;表5 则为单独的ILS以及GBAS/ILS联合系统的数据统计。表4和表5 主要包括水平和垂直方向的置信度及均方误差,其中均方误差(Mean Square Error,MSE)定义为 表4 正常情况下单独GBAS和GBAS/ILS联合系统的数据统计Tab.4 Data statistics of GBAS and GBAS/ILS joint system under normal conditions 表5 正常情况下单独ILS和GBAS/ILS联合系统的数据统计Tab.5 Data statistics of ILS and GBAS/ILS joint system under normal conditions 其中,N为飞行数据采样点数,v为实际值或数据融合输出值,tv为真值。 由表4 可知,数据融合前,GBAS 在水平和垂直方向均满足Ⅰ类精密进近的精度要求。经数据融合算法处理后,GBAS/ILS 联合系统在水平方向的误差相较于融合前的GBAS 略有增加,但仍满足Ⅰ类精密进近的精度要求;垂直方向的误差相较于融合前更小,置信度更高,满足Ⅰ类精密进近的精度要求。 由表5 可知,数据融合前,ILS 在水平和垂直方向均满Ⅰ类精密进近的精度要求。经数据融合算法处理后,GBAS/ILS 联合系统在水平方向的误差相较于融合前的ILS 明显减小,垂直方向的误差相较于融合前基本不变,GBAS/ILS 联合系统在水平和垂直方向满足Ⅰ类精密进近的精度要求。 (1)仿真条件设置 飞机速度vP为70 m/s,电离层风暴g的上限为500 mm/km,w取30 km,vI与vP保持一致。仿真采用2019 年4 月GPS 第3 周历书数据。GBAS 关键点及地面基准站的坐标如表2所示。 GBAS 受电离层风暴的影响,ILS 受弱多径效应影响,利用数据融合算法对其处理。遗忘因子b取0.99,飞机的初始状态与表3相同,状态噪声方差阵Q=diag(10-14,10-14,10-7),表6 为不同斜坡梯度对应的GBAS数据融合观测噪声方差阵初始值R0。 表6 GBAS数据融合观测噪声方差阵初始值Tab.6 Initial value of observation noise variance matrix for GBAS data fusion (2)仿真结果及分析 图6 和图7 为在电离层风暴影响下,g取不同值时,GBAS的水平位置误差和垂直位置误差。g=0的曲线对应无电离层风暴影响,GBAS 的水平位置误差和垂直位置误差均满足CAT I的精度要求。限于篇幅,仅给出电离层风暴影响下4 次飞行中第1 次飞行时,单独的GBAS 和GBAS/ILS 联合系统水平和垂直误差,如图8 和图9 所示。表7 给出了单独的GBAS 和GBAS/ILS联合系统这4次飞行的有关数据统计,每种斜坡梯度后依次对应4 次飞行的数据统计。 图6 电离层风暴时GBAS水平位置误差Fig.6 Horizontal position error of GBAS during ionospheric storm 图7 电离层风暴时GBAS垂直位置误差Fig.7 Vertical position error of GBAS during ionospheric storm 图8 电离层风暴时单独的GBAS以及GBAS/ILS联合系统水平误差(第1次飞行)Fig.8 Horizontal error of GBAS and GBAS/ILS joint system during ionospheric storm(first flight) 图9 电离层风暴时单独的GBAS以及GBAS/ILS联合系统垂直误差(第1次飞行)Fig.9 Vertical error of GBAS and GBAS/ILS joint system during ionospheric storm(first flight) 由表7 可知,在电离层风暴影响下,数据融合前,GBAS 在水平方向满足CAT I 的精度要求,而在垂直方向不满足;经数据融合后,GBAS/ILS 联合系统在水平和垂直方向的误差相较于融合前更小,且在水平和垂直方向均达CAT I 的精度要求,从而提高了精密进近运行的生存能力。 表7 电离层风暴时单独的GBAS和GBAS/ILS联合系统的数据统计(4次飞行)Tab.7 Data statistics of GBAS and GBAS/ILS joint system during ionospheric storm(four flights) (1)仿真条件设置 LOC 阵列天线由8副水平极化的对数周期天线组成[26],相邻阵元间隔为,λ为载波波长,表8 为LOC阵列天线的馈电。 表8 LOC阵列天线的馈电Tab.8 Feeding of LOC array antenna 图3中,假设dR1为1 km。机载LOC 接收机利用带通滤波器处理eP,能够得到150 Hz 信号、90 Hz 信号及载波信号的幅值,进而可计算多径情况下的DDM。对于下滑信标,飞机按照标称3°下滑角进近着陆,多径效应干扰下的DDM可按式(6)进行计算。 设ILS受多径干扰,GBAS 处于正常状态。利用数据融合算法对其处理。遗忘因子b取值为0.99,飞机的初始状态与表3 相同,状态噪声方差阵Q=diag(10-14,10-14,10-7),表9 为ILS 数据融合观测噪声方差阵初始值R0。ILS关键点坐标在表2中给出。 表9 ILS数据融合观测噪声方差阵初始值Tab.9 Initial value of observation noise variance matrix for ILS data fusion (2)仿真结果及分析 限于篇幅,仅给出多径效应影响下4 次飞行中第1 次飞行时,单独的ILS 和GBAS/ILS 联合系统水平和垂直误差,如图10 和图11 所示。表10 为4 次飞行中进近阶段单独的ILS 和GBAS/ILS 联合系统的相应数据统计,每种情况后依次对应4 次飞行的数据统计。 图10 多径干扰时单独的ILS以及GBAS/ILS联合系统水平误差(第1次飞行)Fig.10 Horizontal error of ILS and GBAS/ILS joint system under multipath interference(first flight) 图11 多径干扰时单独的ILS以及GBAS/ILS联合系统垂直误差(第1次飞行)Fig.11 Vertical error of ILS and GBAS/ILS joint system under multipath interference(first flight) 由表10可知,在多径效应影响下,数据融合前,ILS 在水平和垂直方向均不满足CAT I 的位置精度要求;但经数据融合算法处理后,GBAS/ILS 联合系统在水平和垂直方向的位置误差相较于融合前明显减小,且完全满足CAT I的位置精度要求。 表10 多径干扰时单独的ILS以及GBAS/ILS联合系统数据统计(4次飞行)Tab.10 Data statistics of ILS and GBAS/ILS joint system in case of multipath interference(four flights) 本文研究了电离层风暴对GBAS 的影响以及多径效应对ILS 的影响,在实现GBAS 与ILS 时空对准基础上,通过解析从X-Plane 采集的多次进近着陆飞行数据,建立了飞机在进近着陆阶段的运动模型,提出了一种基于Sage-Husa 自适应滤波和方差估计学习算法的GBAS 与ILS 数据融合方法。仿真结果表明,该方法能有效抑制电离层风暴对GBAS的影响以及多径效应对ILS 的干扰,使GBAS/ILS 联合导航系统在干扰条件下,能为飞机提供满足I 类精密进近精度要求的水平和垂直引导,保证飞机安全进近着陆。



4 仿真实验及分析
4.1 正常情况数据融合





4.2 融合算法对电离层风暴影响的抑制


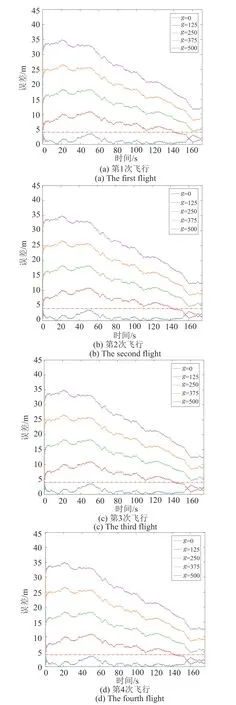
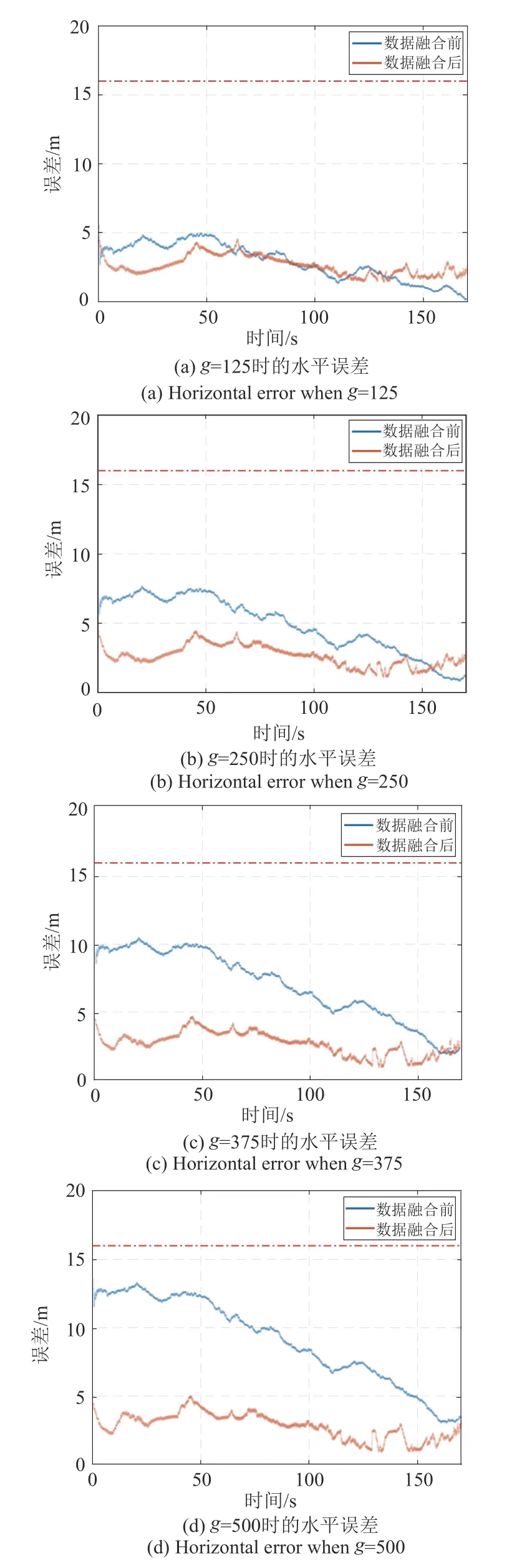


4.3 融合算法对多径效应影响的抑制





5 结论

