融合注意力机制SimAM 的CNN-MogrifierLSTM 航班延误波及预测

屈景怡 张金杰 赵娅倩 李云龙

（1.中国民航大学天津市智能信号与图像处理重点实验室，天津 300300；2.上海民航华东通信网络发展有限公司，上海 200355）

1 引言

随着空中交通流量的增加，航班延误问题给民航的正常运转带来了挑战。某一机场产生的航班延误会在空中交通网络内部进行传播，航线密集的枢纽机场一旦发生航班延误，延误更容易直接传播至其他中小型机场［1］。提前对航班延误波及问题进行准确的预测，可以提高航班延误预警水平，减小航空公司和机场的经济损失，提高旅客出行满意度。

在班延误波及预测的问题上，国内外学者们多结合航班延误影响因素、机场繁忙程度、航班计划等进行研究。目前已有的方法多基于概率论的方法来计算连续航班延误落在不同区间的条件概率［2-4］，文献［5］考虑机场放行能力约束条件来对航班延误波及进行分析，对延误时长进行了定量预测，提升了预测准确率；文献［6］通过马尔科夫毯网络建立了航班计划的多个属性和延误波及变化的贝叶斯网络模型，来研究航班计划对于航班延误波及传播的影响。但以上大多是用小样本数据对航班延误波及问题产生的原因进行研究，面对数据量达到百万级的航班数据，如何有效的对航班延误中复杂关系进行分析挖掘，深度学习是目前研究中使用最为广泛的方法之一。文献［7］使用SE-DenseNet模型加强了信息间的传递对航班延误进行预测；文献［8］提出基于区域残差和LSTM 网络有效提取机场延误数据的时间相关性；文献［9］使用时空图卷积神经网络对离港延误时长进行预测。虽然这些方法对单航班延误程度的预测均有效提高了预测准确率，但并未考虑航班间的波及问题。近年来，逐渐有学者尝试将深度学习用于航班延误波及的研究中，文献［10］构建基于CBAM-CondenseNet 的航班延误波及预测模型，文献［11］提出双向LSTMCatboost 的航班链式延误预测模型，用Catboost 取代全连接层对航班波及延误时长进行预测。航班延误波及预测属于基于时序信息的预测，又包含丰富的空间信息［12］。但这两种模型并未对航班延误波及中的时序与空间属性同时进行特征提取。

长短时记忆网络（Long Short-Term Memory，LSTM），在时间维度上对先前时序信息能够记忆的更为深刻，但使LSTM 中输入的x和之前状态hprev在输入细胞前是相互独立的，MogrifierLSTM 使这两个输入从完全独立到自主交互很好的提升了网络性能［13］。TCN 作为时间卷积网络融合了膨胀卷积和ResNet 残差结构，弥补了传统卷积神经网络提取时序信息不足的缺点，但是需要足够长的原始输入信息才能保证获取到历史信息［14-17］。由于航班波及的航班数量有限，构成时序数据集的序列长度有限，所以本文使用CNN 网络与MogrifierLSTM 对航班延误波及问题进行预测，并融合注意力模块SimAM 来提高预测准确率。目前普遍使用的SE 模块文献为通道注意模块，但其只针对通道而忽略了空间，CBAM 模块在通道注意的基础上增加了空间注意力，但两者并不是同时进行；文献［18］提出的Si⁃mAM不同于现有的通道空间注意力模块，该模块无需额外参数为特征图推导出3D 注意力权值，可以更好对关键特征的提取进行同时强化。

针对航班延误波及的空时特性，本文先后提出两种不同类型的航班延误波及数据集的构造方法，又提出融合注意力机制SimAM 的CNN-MogrifierLSTM航班延误波及预测方法，不仅采用了卷积神经网络在空间特征提取的优势又考虑了形变长短时记忆网络在处理时序信息的优越性，并用注意力机制模块对特征矩阵进行重要神经元增强。实现同一架飞机在执行不同航班任务时，根据航班延误波及的传播规律对后续航班的延误等级进行分类预测，为有关民航部门控制延误波及提供相应建议。

2 航班链式模型建立

航班延误具有时空分布的特性，当同一架飞机连续执行不同的航班任务时，由于前一架飞机的延误而导致后续航班继续延误的情况常有发生。定义同一架航空器在一定时间范围内第一次起飞的机场为一级机场。航空器从一级起飞机场执行航班任务1 到达的机场称为二级机场，也称为一级到达机场或二级起飞机场。以此类推，多个机场由同一架航空器Z 在不同机场间执行飞行任务联系，从而构成航班链，如图1 所示。以“北京-上海-广州”为例，定义北京为一级机场，同一架飞机执行航班任务1 从北京飞往上海，上海就是航班链中的二级机场，也叫一级到达机场或二级起飞机场；该飞机又从上海出发执行航班任务2 从上海飞往广州，广州就是航班链中的三级机场，也叫二级到达机场或三级起飞机场。

图1 航班链模型Fig.1 Flight chain model

3 融合注意力机制SimAM的CNN-Mogrifier-LSTM 网络混合模型

3.1 网络描述

CNN 在预测中难以学习时序数据之间的关系，由于航班链数据具有时序性，因此对航班延误波及问题进行预测需要循环神经网络系列方法的强化。CNN-LSTM 网络结构图如图2（a）所示，本文提出的融合注意力机制SimAM 的CNN-MogrifierLSTM 网络模型如图2（b）所示。

本文网络先通过四个融合SimAM 的结构块，每个结构块采用1×1 卷积，然后使用两个3×3 卷积进行特征的提取，最后使用1×1卷积进行融合，每个卷积层都通过分组来保证其时序的独立性，再通过Si⁃mAM 模块进行通道和空间上的同步加权。卷积完成后通过平均池化筛选卷积层已提取的特征，最后数据经过全连接层送入MogrifierLSTM 中预测，融合注意力机制SimAM 的CNN-MogrifierLSTM 网络对针对强空间航班链数据集的网络配置如下表1 所示，数据集具体构造方法见本文4.2节。

表1 网络结构配置Tab.1 Network structure configuration table

图2（b）中使用的SimAM 模块如图3（c）所示，改进了通道注意力如图3（a）所示与空间注意力如图3（b）所示无法同时进行的优势，C代表通道数，M代表每个通道输入H×W矩阵的维度。引用神经科学中信息丰富的神经元通常表现出与周围神经元不同的放电模式并会抑制周围神经元，具有空域抑制效应的神经元应当赋予更高的重要性，定义了如公式（1）所示的能量函数。

图2 网络结构示意图Fig.2 Diagram of network structure

图3 注意力对比示意图Fig.3 Attention contrast diagram

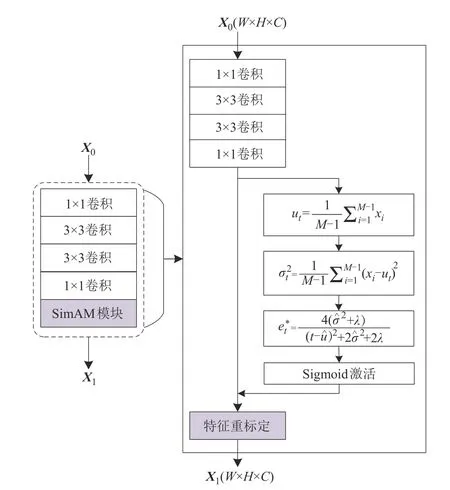
图4 融合SimAM单个结构块Fig.4 Fusion of SimAM structural block

LSTM 一直被广泛应用在各类与时序相关的任务中［19］，MogrifierLSTM 在不改变LSTM 本身的结构下，让上一时刻的隐藏层状态hprev和当前时刻的输入x在输入当前神经元前就进行了交互，增强了上下文的建模能力。交替地让x和hprev交互进行QR分解如公式（3）所示。

其中Cprev代表前一个MogrifierLSTM 单元的细胞状态，hprev表示隐藏层状态。定义为中上标最大的那个值，如公式（4）与公式（5）所示。Mog⁃rifierLSTM 架构中的hprev，Cprev是前一个细胞的隐藏层状态，在初始化的时均采用从0初始化，以保持每个序列中互不干扰。但在更新隐藏层参数时，采用的是随机初始化。

3.2 网络反向传播

本文网络的反向传播过程通过梯度下降算法逐层迭代，根据误差项实现更新参数直至网络收敛。融合注意力机制SimAM 的CNN-MogrifierLSTM在反向传播的过程中分为MogrifierLSTM 模块与融合SimAM的CNN模块，反向传播过程如图5所示。

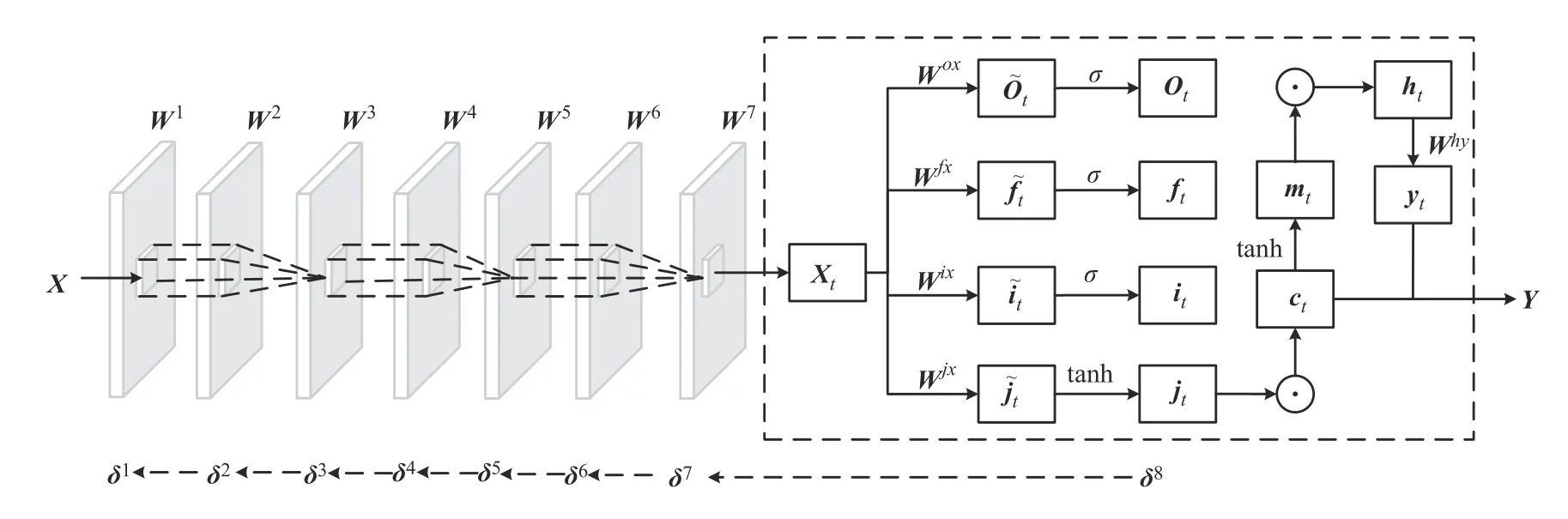
图5 网络反向传播图Fig.5 Network back propagation

MogrifierLSTM 在不改变LSTM 本身的结构下，根据梯度下降算法，先对MogrifierLSTM 网络反向传播过程中的误差项进行推导，据误差反向传播原理，推导得出误差沿网络层数的反向传播过程为式（6）所示。其中分别代表每个记忆细胞中各个门的误差项如式（7）～（10）所示。依次表示输入门、遗忘门、输出门的权重矩阵。

其中f（·）为激活函数，f（·）'为激活函数的导数。上标l代表当前层，下标t代表当前时刻。卷积模块内各个隐藏层的误差计算如式（11）～（17）所示。其中δ1，δ2…δ7分别表示对应层的误差项，U1，U2，…U6为各层的输出特征映射，W表示每层的之间的映射矩阵。

4 融合注意力机制SimAM的CNN-Mogrifier-LSTM 航班延误波及预测

融合注意力机制SimAM 的CNN-MogrifierLSTM航班延误波及结构图如图6 所示，主要包括航班链数据集构造、特征提取、分类预测三部分，下面主要对航班链数据集构造与分类预测展开描述。

图6 航班延误波及预测模型总体结构图Fig.6 Overall structure diagram of flight delay ripple prediction model

4.1 数据集介绍

本文所使用的航班数据为中国民用航空华东地区空中交通管理局所提供的2018年3月到2019年5月全国航班飞行数据，其中关键的样本属性包括航班号、飞机编号、实际起飞/到达机场、飞行航迹、计划出发/到达时间、实际出发/到达时间、目标/实际撤轮档时间、计划起飞/到达机场、计划机型、巡航高度、巡航速度、军方批号、保障种类、保障类型等38 个属性。这些特征属性都与该条航班是否延误有密切的关联，不仅包含了重要的空间特征，也包含了丰富的时间信息。由于空管局所提供航班数据中有部分异常值与空值，所以先对原始航班数据集选择目前主流的数据分析库Pandas 进行数据清洗。

4.2 航班链数据集构造

根据航班延误波及的空时特点，本文首先尝试了以空间信息为主的强空间航班链数据集的构造方法，为了增强其时间上的关联性又提出了强时序航班链数据集的构造方法。在强空间航班链数据集中可以根据往日同一航班链延误情况对延误等级进行预测，强时序航班链数据集中上一次航班的延误状态会直接影响下一次航班的延误程度。

4.2.1 强空间航班链数据集构建

根据第2 章中航班链式模型的定义，每次执行航班的到达机场与执行下一次航班的起飞机场为同一机场，本文根据同一架航空器在24小时内空间维度上的变化构成强空间航班链数据集。首先选定飞机编号（航空器编号）、航班执行日期、一级到达机场、二级起飞机场四个属性作为数据融合的键值，对清洗后的航班数据集进行第一次数据融合，融合后去除二级机场起飞时间早于一级机场到达二级机场时间的异常航班链，此时航班链数据集中该飞行器执行了两次航班任务，在空间上周转了三个机场。延误波及现象的产生有逐级传递的特性，以此类推本文对数据进行了三次融合，然后对融合后的航班链数据集根据一级机场的起飞时间对所有的航班链数据集进行时间轴上排序，构成最终的强空间航班链数据集，每条数据中的航空器连续执行了四次航班飞行任务，空间维度涉及五个机场的中转情况，航班链的延误标签为第4 次航班任务的延误等级。大多数飞机在执行完一次飞行任务后当日并不会再执行其他的飞行任务，随着在同一天内执行飞行任务的增多，可研究的航班链数据集的数据量也会越来越少，所以本文主要研究由连续执行四次航班任务构成的航班链延误波及情况。最后将强空间航班链数据集中的特征属性划分为数值型与离散型，数值型特征采用Min-Max 归一化编码，离散型特征采用Catboost编码。

为了更清楚的对强空间数据集进行描述。定义强空间航班链数据集Fa中第i条航班链数据用fi=(fi1，fi2，fi3，fi4)表示。其中fi1，fi2，fi3，fi4分别代表这条航班链数据fi包含在时间维度上前后执行航班任务的四条单航班信息。Fa数据集进一步可以用Fa={(f11，f12，f13，f14)，(f21，f22，f23，f24)，(f31，f32，f33，f34)，…}(fn1，fn2，fn3，fn4) 表示。

4.2.2 强时序航班链数据集构建

强空间航班链数据集的每条航班链数据中包含多级机场丰富的空间信息，但时序信息只包含在相邻的航班链中，为了进一步研究航班链内部的时序性，本节提出了第二种数据集构造方法，如图7强时序航班链数据集构造图所示。

图7 强时序航班链数据集结构图Fig.7 Strong temporal flight chain data construction

由于每条航班链数据在时间维度上执行航班任务有前后顺序，前序航班的延误会对后续航班的延误会有较大的影响，所以对每条强空间航班链数据进行数据分割。为满足不同情况下的预测需求，分别构建强时序性航班链数据集Fb，Fc，Fd分别表示为：

其中强时序航班链数据集Fb只根据第一次航班与第二次航班的数据来预测第二次航班的延误程度，融合注意力机制SimAM 的CNN-Mogrifier LSTM 网络的步长设为2。强时序航班链数据集Fc根据第一次航班、第二次航班与第三次航班的数据来预测第三次航班的延误程度，步长设为3。强时序航班链数据集Fd根据第一次航班、第二次航班、第三次航班与第四次航班的数据来预测第四次航班的延误程度，步长设为4。不同的强时序航班链数据集可以训练不同的网络模型供空管部门使用，其数据集总量增至强空间数据集的2倍、3倍、4倍。

4.3 分类预测

根据《航班正常管理规定》［20］中“航班延误”的相关定义，将航班延误情况进行细分得到五个延误等级，并对不同的等级划分延误等级数，其判定标准如表2中所示。等级标签根据数据集中的计划到达时间与实际到达时间进行差值计算，最终用Soft⁃max分类器得到航班延误预测等级。

表2 航班延误等级划分Tab.2 Classification of flight delays

根据预测出的最大概率的延误等级，决定模型输出航班延误波及的预测结果。为了评估融合注意力机制SimAM 的CNN-MogrifierLSTM 模型分类的效果，本文使用准确率作为评估指标，即模型预测结果正确的数量占数据总量的比值，如公式（18）所示。N代表航班链数据集样本总量，L代表延误程度的五种类别，Si代表验证集中延误等级为i时预测结果正确的航班链数据量。

5 实验结果与分析

实验环境为戴尔PoweredgeR370 机架式服务器，16G 显存，双Intel XeonE5-2630 CPU，CPU 频率为2.20GHz，GPU 加速显卡为NVIDIA P100，软件的运行环境为Ubuntu16.04 操作系统搭建的Pytorch深度学习框架。

5.1 模型参数设计

本文实验所使用的原始航班数据共1048576条，经过数据清洗与航班链数据集构造后，航班延误波及预测实验最终使用的强空间航班链数据集Fa的数据量为36287条；根据前一次航班延误程度预测下一次航班延误的强时序航班链数据集Fb的数据量为72574条；根据前两次航班延误程度预测下一次航班延误的强时序航班链数据集Fc的数据量为108861条；根据前三次航班延误程度预测下一次航班延误的强时序航班链数据集Fd的数据量为145148条；训练集和验证集划分比例为5∶1。在经过多次实验与参数调整后，融合注意力机制SimAM 的CNNMogrifierLSTM 网络的实验环境参数选取信息如表3所示。

表3 实验环境参数Tab.3 Experimental environment parameters

融合SimAM 的CNN-MogrifierLSTM 卷积滤波器的数量为64 个，步长为默认值1，同时对边界进行Padding 补0 填充保证输入卷积层后输出尺寸不发生变化；池化层采用平均池化方式，池化尺寸为2×2，步长也设为1；然后输入一层MogrifierLSTM 网络中，隐藏层维数256。

5.2 强空间航班链数据集结果分析

MogrifierLSTM 网络在提取时间序列信息的过程中，序列的步长对最终的预测输出有着直接的影响。如果输入网络的步长太短，可能会弱化数据之间的相关性，有效的时间信息不能被充分学习；反之输入的步长太长，训练过程中可能会存在梯度消失甚至梯度爆炸现象。表4列举了对于强空间航班链数据集Fa使用融合SimAM 的CNN-MogrifierLSTM混合网络模型不同步长对应的准确率。

表4 强空间航班链数据集序列长度准确率对比Tab.4 Comparison of sequence length accuracy rates in strong space flight chain data

通过实验结果发现，强空间航班链数据集Fa的序列长度等于8 的时候，预测结果的准确率最高为78.79%。在步长选择合适的情况下，在对未来航班延误波及进行预测可以产生很好的时间相关性，但随着步长增加，在时间维度上会学习到更多不需要的冗余数据，造成准确率的下降。本文后续对强空间航班链数据集的航班延误波及预测的步长取值均选用8。

5.3 不同航班链数据集结果分析

强空间航班链数据集在时间上参考前序飞行计划相同的航班链数据，航班延误波及信息更多在空间维度上体现。强时序航班链数据集直接根据同一架飞行器前几次飞行任务情况来对后续执行的航班进行延误预测，时序性更强。在飞机实际执行航班任务的时候，连续执行两次航班任务的情况比较多，连续执行三次任务的情况会相对减少，连续执行四次任务会更少为了使模型在实际预测中具有更好的适用性，针对这三种情况分别构建了连续执行两次航班任务数据集Fb，连续执行三次航班任务数据集Fc，连续执行四次航班任务数据集的强时序数据集Fd，不同数据集的实验结果对比如图8所示，其中8（a）为延误等级分类准确率对比，8（b）为损失值对比。

图8 不同数据集对比Fig.8 Comparison of different data sets

从图中可以看出三种强时序链数据集在准确率上相比强空间数据集有了很大的提升，准确率最好的是连续执行四次航班任务的数据集Fd，准确率达到了93.16%，相比于强空间数据集Fa的准确率78.79%提升了14.37%，损失值也最低。将三种强时序航班链数据集进行对比发现随着连续执行航班次数的增多，时序性也在增强，预测准确率也在逐步提升。

5.4 交替轮数对预测结果的影响

交替轮数r值是MogrifierLSTM 网络中一个重要的超参数，r值越大x输入LSTM 网络前和之前细胞的状态交互越充分，网络更好挖掘时序信息之间的关联性。但是r值每增加1，每次更LSTM 细胞状态时就要多进行一次QR 矩阵分解，网络计算量与训练时间都会大幅度的增加。由于实验硬件设施算力有限，所以实验r最多设为6。表5 为交替轮数r增加时，航班延误波及预测的准确率与每轮训练时间在两种数据集上的实验结果。本文实验对训练模型耗时要求不是很高，所以优先考虑对准确率的影响，故强空间航班链数据集Fa的r值设为6，强时序航班链数据集Fd的r值也设为6。

表5 交替轮数r对准确率与训练时间的对比Tab.5 Alternating rounds r for accuracy and training time

5.5 算法复杂度

空间复杂度与时间复杂度是表示算法复杂度的两个重要指标。空间复杂度用来计算资源的消耗程度，模型参数用Params 衡量，算法越复杂，参数量越多。时间复杂度用浮点运算次数FLOPs 衡量，算法复杂度越高，模型训练和预测的时间都会变长。表6 为本文融合注意力机制SimAM 的CNNMogrifierLSTM 模型与其他几种模型的复杂度对比，其中MogrifierLSTM 简写为MLSTM。从表6 中可以看出，MLSTM 相比于LSTM 算法复杂度并无很大增加，在CNN-MLSTM 中融入注意力机制SimAM 模块后参数量增基本不发生变化，进一步验证了SimAM模块的无参特性。并使用1000 条验证集数据对模型进行了预测时间分析，结果如表6 所示。不同模型平均每条航班的预测时长差值都在0.001 秒以内，证明了该模型虽然复杂度有所增加，但实际预测耗时并无很大变化。空管局对预测实时性的要求为预测一条数据在一秒以内，所以牺牲复杂度提高准确率在实际运用中是可行的。

表6 不同网络模型算法复杂度对比Tab.6 Network model algorithm comcexity comparison

5.6 不同网络模型结果分析

为了测试融合SimAM 注意力机制的CNN-MogrifierLSTM 网络的性能，本节在强空间数据集Fa与强时序数据集Fd两种数据集上分别使用CNN、LSTM、MogrifierLSTM、CNN-LSTM、CNN-MogrifierLSTM五种模型与本文提出的SimAM-CNN-MogrifierLSTM网络模型进行准确率与损失值的对比实验。对于强空间数据集Fa不同模型的对比实验结果如图9所示，强时序数据集Fd不同模型的准确率对比实验结果如图10 所示，（a）为准确率对比，（b）为损失值对比。

图9 强空间数据集不同模型性能对比Fig.9 Strong spatial data set comparison

图10 强时序数据集不同模型性能对比Fig.10 Strong sequential data set comparison

从实验结果可以看出在时序的基础上加上卷积思想后的CNN-MogrifierLSTM 网络在两种数据集上相比单独的CNN网络或LSTM网络的准确率都有了明显的提升，在强空间数据集上，相比CNN 网络提升了2.38%，相比LSTM 网络提升了2.24%；在强时序数据集上，分别提升了16.46%与2.16%。本文对CNN-MogrifierLSTM 加入SimAM 注意力机制模块后，在强空间数据集上相比CNN-MLSTM 又提升了0.62%达到了78.79%，在强时序数据集上提升了0.53%达到了93.16%，明显高于其他五种网络的准确率，损失函数值也最低。综合说明本文提出的融合注意力机制SimAM 的CNN-MogrifierLSTM 网络在进行航班延误波及预测时，预测出的航班延误波及分类结果与实际最为接近，网络性能最优。

为了进一步验证运用深度学习模型在大数据基础上对航班延误预测的准确率相比于传统算法有很大提升。分别用几种不同的航班预测模型［21-23］与本文模型进行对比，实验对比如表7 所示。传统的机器学习是属于小样本学习，对于大数据的训练效果不是很好。从数据的属性分析，航班数据其属性之间具有依赖性，而传统的如C4.5在选择属性是没有考虑到属性间的相关。支持向量机通过求解凸二次规划问题得到一个局部最优解，也为全局最优解，而航班数据的每一条之间其差异性较小。贝叶斯网络使用的前提是属性之间相互独立，而该假设并不适用于本数据集。人工神经网络的可以充分的学习属性之间的相关性，但是无法估计每条数据之间的关联性。本文模型同时考虑到了数据属性之间与数据序列间的关系，采用CNN 融合注意进行空间的特征融合，采用MogrifierLSTM 对每条数据间的时序性进行特征提取，因此本文所提出的网络模型更适用于对航班延误波及等级进行预测。

表7 传统模型准确率对比Tab.7 Accuracy comparison of traditional models

6 结论

本文针对航班延误波及问题提出了一种融合SimAM 注意力机制的CNN-MogrifierLSTM 航班延误波及预测方法。通过SimAM 注意力机制模块对重要特征进行通道与空间的同步加强，并结合CNN 提取空间信息与MogrifierLSTM 提取时间信息的优势，对融合空时信息的航班链数据进行充分的特征提取，通过大量实验验证了该网络模型的有效性。

（1）通过分析航班延误波及的传播规律，提出两种航班链数据集的构造方法。首先对数据清洗后的航班数据进行三次复杂融合，提出强空间数据集的构造方法；为了进一步增强时序性提高预测准确率，对强空间数据集进行顺序分割，提出强时序航班链数据集的构造方法，增强预测的适用性，可以根据波及的次数选择适用于网络训练的不同数据集。

（2）基于航班链数据集的空时特性，提出融合SimAM 注意力机制的CNN-MogrifierLSTM 网络模型。首先使用CNN 网络层对空间信息进行提取，然后通过SimAM 注意力机制模块进行空间和通道的同步注意对重要特征进行增强，最后输入Mogrifi⁃erLSTM 进一步提取航班延误波及中的时序特性，有效提升了航班延误波及预测的准确率。

对航班延误波及问题提前进行准确的预测，可以有效提升低质量航班质量，减少航班延误波及的发生。在下一阶段，将考虑如何使用回归模型来对延误的具体时间进行预测，同时在数据允许的情况下，增加天气等影响因素对航班延误波及进行分析。