阵列雷达的分层介质目标频域匹配滤波成像算法
邓桂林 马昭阳 曾 旸 邓 彬 王宏强
(1.国防科技大学电子科学学院,湖南长沙 410073;2.中国人民解放军第78156部队,重庆 400000)
1 引言
随着材料技术的不断发展,复合材料、高分子材料等新型非金属介质材料因具备优良的物理化学特性及相对低廉的制造成本,而被广泛运用于工业生产、基础设施建设、三维(Three-Dimensional,3D)打印等多个领域,如常见的水泥结构、高温隔热结构、桥梁减震塑料垫、瓷砖等都是以非金属介质材料为主体的结构件[1]。这些非金属材料结构件在生产或使用过程中,可能形成诸如掺杂、空腔或裂痕等缺陷,导致介质材料结构件在使用过程存在安全隐患,甚至造成灾难性事故[2]。因此,对介质材料结构件的内部完好性进行检测是非常必要的,快速发展的无损检测(Non-Destructive Testing,NDT)技术为这些应用需求提供了技术支持。
NDT 技术可以在不影响介质材料物理化学特性、不破坏介质材料结构件内部结构的前提下,实现对介质材料结构件内部结构的分析检测。由于毫米波(Millimeter Wave,MMW)对大多数非金属介质材料具有适中的穿透性[3],这使得MMW 在介质材料结构件的NDT 应用中具有巨大的发展潜力。与超声检测[4]、涡流检测[5]、X 射线检测[6]等传统NDT 技术相比,MMW 具备成像分辨率高、易实现大带宽、光子能量低等相对优势,使得基于MMW 平面阵列雷达近场3D 成像的NDT 技术受到了越来越多关注,目前MMW 平面阵列雷达近场3D 成像技术已经在快速安检、隐蔽武器检查、人体安检等NDT 相关应用领域[7-8]得到了大量研究和广泛运用。
典型的MMW 平面阵列雷达近场3D 成像技术[7-8]主要基于自由空间假设,即假设成像目标为位于自由空间中的金属目标。然而随着非金属介质材料的大量运用,越来越多的NDT 应用涉及到电介质结构,如对高温隔热结构、桥梁减震塑料垫的无损检测。由于电介质结构将对电磁波的传播特性造成影响,改变电磁波的传播速度和传播方向,且介质材料的相对介电常数越大,这种影响也将越明显[9],自由空间假设将不再符合实际应用场景,导致基于自由空间假设的MMW 平面阵列雷达近场3D成像算法无法直接运用于介质目标成像。
为消除介质材料对电磁波传播的影响,研究人员提出了一种改进的后向投影(Improved Back Projection,IBP)算法[10-11]。该算法在实现过程中,首先需要根据Snell 定律计算电磁波在介质分界面上的折射点,从而得到电磁波在介质中传播的准确路径,进而在成像区域内进行精确投影,实现高质量成像。其实现原理决定了IBP 算法具备适应性强、鲁棒性好、成像质量好等优点,理论上适合任意阵列体制对任意形状介质目标进行成像,Ingrid Ullmann 等[12]利用该算法实现了平面阵列对任意形状介质目标的成像。基于IBP 算法的上述突出优点,IBP 算法也常常作为参考算法。但在该算法的实现过程中,电磁波在介质分界面上折射点的计算及投影操作均需要特别大的运算量,这导致IBP 算法的成像速度很慢。为进一步提高成像速度,参考阵列雷达成像的距离偏移(Range Migration,RM)算法,文献[13]提出了一种适用于半空间介质目标成像的分层RM(Layered RM,LRM)算法,该算法基于不连续波场推导得到,首先在波数域将雷达的回波数据偏移至介质分界面,然后再按照经典RM 算法的步骤实现成像,因此LRM 算法继承了RM 算法高效的特点,但该算法仅适用于半空间介质目标成像。为实现对多层介质目标的快速成像,一类基于多层介质格林函数的分层介质目标衍射层析成像(Diffraction Tomography,DT)算法[14-16]被提了出来,如相移偏移(Phase Shift Migration,PSM)算法[15],与IBP 算法和LRM 算法不同的是,这一类算法通常基于分层介质格林函数和一些近似条件推导得到。由于DT 算法在实现过程中使用了快速傅里叶变换(Fast Fourier Transform,FFT)和逆FFT(Inverse FFT,IFFT)运算,因此,该类算法也具备成像速度快、成像效率高等突出优点,但由于格林函数的闭合形式高度依赖于介质目标的几何结构,导致该类算法往往仅适用于特定结构的介质目标成像,且这类算法大多关注多层介质中的最后一层半空间介质目标成像,而非整个介质区域的成像[17-18],这在一定程度上限制了衍射层析成像算法的应用。
为实现对平面多层介质目标的快速成像检测,本文提出了一种基于频域匹配滤波(Frequency Domain Matched Filter,FDMF)的单发单收(Single-Input-Single-Output,SISO)阵列雷达分层介质目标成像算法。首先将SISO 阵列雷达单个阵元的时域回波数据变换至频域,然后利用电磁波在平面分层介质之间传播时电磁波平行于介质分界面的分量将保持连续这一规律,在频域化简雷达的回波模型,得到了一个与电磁波在介质分界面上折射点无关的频域回波模型;然后将阵列雷达的空域回波信号变换至波数域,并通过相位补偿和累加求和操作实现对介质区域进行成像检测。与同样适用于多层介质目标成像的IBP 算法相比,所提算法避免了电磁波折射点的计算,从而可以降低成像运算复杂度,实现快速成像。与波数域算法PSM 算法相比,仍有一定的计算优势。
本文的具体结构如下:在第2 节中推导了分层介质目标的FDMF 算法;在第3 节中进行了数值仿真,并将FDMF 算法的成像结果与IBP 算法[12]、PSM算法[15]的成像结果进行了比较;在第4 节中开展了实验测量,验证FDMF 算法对雷达实测数据的处理能力;第5节对全文进行了总结。
2 成像模型与算法
根据电磁学原理可知,电磁波在连续均匀介质中传播时,不会发生散射或折射。但电磁波在传播过程中遇到掺杂或空腔等介电参数突变的结构时,电磁波的传播速度和传播方向会发生改变,同时向外辐射一定功率的电磁波[13]。通常,这些能引起电磁波发生散射的掺杂或空腔等特殊结构,即是介质内部的缺陷结构,因此可以定义介质目标的反射率函数O(r)来描述介质的内部结构。通过阵列雷达接收的回波数据反演介质目标的反射率函数O(r),即可实现对介质目标内部结构进行成像,以达到对介质构件内部结构进行无损检测的目的。
如图1 所示,假设平面分层介质结构各层均由各向同性介质组成,在y轴方向是分层的,各层的相对介电常数及厚度如图中所示。阵列雷达位于第0层介质(空气)中y=d0平面上,雷达阵元的位置坐标用rR=(xR,yR,zR)表示,也即yR=d0,雷达发射线性调频信号。

图1 平面分层结构示意图及坐标系定义Fig.1 Planar medium structure and the coordinate definition
忽略电磁波的传播损耗,根据射线追踪原理和叠加原理,雷达的接收回波可用(1)表示:

其中t表示雷达发射信号的快时间,V表示雷达的探测区域,r=(x,y,z)表示散射点的位置,n为r处散射点所在的介质层数,p(t)为雷达发射信号,ri为电磁波在第i层介质中传播的距离,ci为电磁波在第i层介质中传播的距离。
ri和ci可按照公式(2)进行计算:

其中c 为真空中的光速,εi为第i层介质的相对介电常数,ai=(xi,yi,zi)为电磁波在第i层介质与第i+1层介质分界面上的折射点。当i取0时,电磁波折射点a0即为雷达坐标;当i为n时,电磁波折射点ai+1即为散射点的坐标r。且电磁波在介质分界面上的折射点ai可以通过Snell定律求得。
分层介质目标成像的典型算法IBP 算法,在成像处理过程中需要计算电磁波的传播时迟,因此,无法避免折射点ai的计算。但ai的求解需要计算二次方程,导致IBP算法计算复杂度高且难以估计。为了避免折射点的求解以降低算法复杂度,可以考虑在频域对雷达回波进行处理。对雷达回波作关于t的傅里叶变换(Fourier Transform,FT),可得雷达回波的频域数据s(rR,|k0|)如(3)所示:

其中P(∙)为雷达发射信号的频域形式,ki=(kxi,kyi,kzi)为电磁波在第i层介质中传播的波数向量,ri为电磁波在第i层介质中传播的路径向量,且ri=ai-ai+1。
根据电磁学理论可知,电磁波在平面分层介质之间传播时,电磁波平行于介质分界面的分量将保持连续,即:
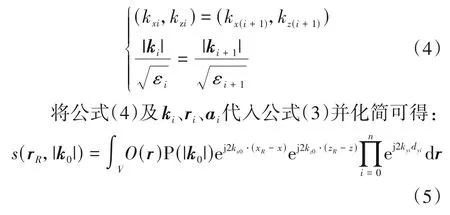
其中y=yi为第i层介质与第i+1层介质的分界面,di为第i层介质的厚度,可用di=yi-yi+1计算得到,当i=n时,dn表示目标点(x,y,z)与其面前一层介质分界面之间的距离,即dn=y-yn-1。
从公式(5)可以看出,将雷达回波从时域变换至频域,并利用公式(4)的波数分量关系对频域回波化简后,雷达回波仅与电磁波在空气中的波数向量k0=(kx0,ky0,kz0)、散射点所在介质中的波数向量其他各层介质中的波数分量kyi、雷达坐标rR、散射点坐标r及各层介质厚度di有关,而与电磁波在各个介质分界面上具体的折射点ai无关。
为了得到雷达回波的空域波数ki,对s(rR,|k0|)作关于xR和zR的FT,代入k0和rR的坐标分量,改变积分顺序后化简公式,可得:

观察公式(6)可以发现,雷达回波从空域变换至频域后,雷达回波实际上是介质反射率函数O(r)乘以一个相位项后再叠加的结果。因此,根据匹配滤波原理,对雷达回波进行相位补偿并叠加,即可得到函数O(r)的像,即:

3 成像结果与分析
为了验证算法的成像性能,本节将进行数值仿真,并将所提算法的成像结果与IBP 算法和PSM 算法的成像结果进行比较。仿真及实验参数如表1所示。

表1 仿真及实验参数Tab.1 Simulation and experimental parameters
3.1 点扩散函数仿真
点扩散函数(Point Spread Function,PSF)是定量分析算法成像性能的重要工具,通过PSF 可以得到衡量算法成像质量好坏典型指标,如冲激响应宽度(Impulse Response Width,IRW)、峰值旁瓣比(Peak Side Lobe Ratio,PSLR)等。辅以成像时间的统计,则可进一步比较算法的成像效率,对算法性能进行综合评价。为了验证FDMF 算法的成像性能,本小节首先进行了PSF 仿真,并以IRW、PSLR、成像时间为指标,将FDMF 算法的成像性能与IBP算法和PSM算法进行了比较。
仿真成像场景如图2(a)所示,空间坐标系中y<0 区域由相对介电常数为2 的各向同性均匀介质构成,y>0 区域为空气。在介质中存在一个用于模拟缺陷结构的理想散射点,其位置坐标为(0 m,-0.05 m,0 m)。使用SISO 阵列雷达对介质区域进行探测,阵列雷达位于空气中y=0.3 m 平面上,阵列雷达中心位于y轴上。IBP算法、PSM算法和FDMF 算法的3D 成像结果分别如图2(b)、图2(c)和图2(d)所示。

图2 单层介质嵌入理想散射点仿真场景及3D成像结果Fig.2 Simulation scene and 3D imaging results of ideal scattering point embedded in monolayer media
将3 种算法的3D 成像结果与成像场景进行对照可以发现,3 种算法均能对介质中的理想散射点进行高质量三维重构成像。为了比较FDMF算法与IBP算法、PSM 算法的3D成像质量,现沿x轴、y轴和z轴作3D 成像结果的切面图,如图3 所示,3 种算法几乎可以得到相同的IRW 和PSLR,其具体数值在表2中给出。


图3 IBP算法、PSM算法和FDMF算法成像结果沿x轴、y轴和z轴的切面对比Fig.3 The comparison of the imaging results’sections along x-,y-and z-axis by the IBP,PSM and FDMF algorithms
表2中还给出了3种算法的成像时间,成像结果沿x轴、y轴、z轴的成像点数分别为101、67、101,成像计算平台均为Intel Core i7-9750H CPU、16 GB 内存笔记本电脑。从表2中数据可以看出,FDMF算法可以在大幅缩减成像时间的情况下,得到与IBP 算法相同的成像性能。与PSM 算法相比,FDMF 算法在成像时间上仍然有一定优势。FDMF 算法的运算优势主要是由于该算法可以通过矩阵乘法实现。

表2 性能比较Tab.2 Performance comparisons
3.2 双层介质中多散射点成像仿真
为了进一步分析FDMF算法对多层介质目标的成像性能,现进行双层介质目标的成像仿真。仿真场景如图4(a)所示,介质区域由两种不同的介质构成,其中-0.075 m 表3 介质相对介电常数与理想散射点位置Tab.3 The relative permittivity and the location of the defects 在双层介质仿真场景中,IBP 算法、PSM 算法和FDMF算法的3D成像结果分别如图4(b)、图4(c)和图4(d)所示,将3种算法的3D成像结果分别与仿真场景图4(a)进行对照可以发现,在3 种算法的成像结果中所有散射点聚焦良好、位置正确,验证了3种算法成像结果的正确性。 图4 双层介质嵌入理想散射点仿真场景及3D成像结果Fig.4 Simulation scene and 3D imaging results of ideal scattering point embedded in double media 首先对3D 成像结果进行分析。从3 种算法的3D成像结果投影图可以发现,不同介质中散射点的成像结果沿x轴和z轴的分辨率大致相同;但沿y轴的分辨率差异明显,散射点所处环境中介质相对介电常数越大,其成像结果的距离分辨率越高。这是由于不同介质中的散射点,其散射的电磁波沿x轴和z轴的波数分量大致相等,因而可以得到了相似的分辨率;但相对介电常数更大的介质中的散射点,其散射电磁波沿y轴的波数分量也更大,相应的其成像分辨率也越高,因而不同介质中的散射点沿y轴方向的分辨率明显不同。 进一步对IBP 算法、PSM 算法和FDMF 算法的双层介质3D 成像结果进行比较,可以直观地发现3种算法的3D 成像结果仍然大致相同。综合3.1 和3.2中的仿真结果可以看出,FDMF算法对多层介质目标成像时,可以获得与IBP算法、PSM 算法相似的成像效果;但在成像效率上,FDMF算法优势明显。 为验证FDMF算法在处理真实雷达数据时的成像性能,本节针对三种不同类型的目标进行了实验测量。实验中的SISO 阵列雷达由矢量网络分析仪和机械扫描架等效构成,实验场景如图5所示,阵列雷达的参数与仿真中的参数保持一致。三种不同类型的实验目标分别如图6(a)、图6(b)、图6(c)所示,各实验目标对应的内部结构示意图分别如图6(d)、图6(e)、图6(f)所示。 图5 实验场景Fig.5 Overview of the experimental scene 实验目标A 为一个内嵌锡箔条的PTFE 块,如图6(a)所示,主要用于验证算法对介质目标中不同深度位置上缺陷的成像性能。该PTFE 块的长宽厚尺寸分别为20 cm、20 cm 和4.5 cm。锡箔条在PTFE 块中的位置分布如图6(d)所示,锡箔条共计6 条,宽均约1 cm,长度为8 cm 至14 cm 不等,按照每组2 条的方式将锡箔条划分为3 组嵌于PTFE 块内,3 组锡箔条分别位于y=-2 cm、y=-3 cm、y=-4 cm 三个不同的平面上。在该模型中,PTFE 块主要用于构建介质环境,不同深度的锡箔条用于模拟介质中不同深度的缺陷结构。 图6 三种实验目标及三种实验目标的缺陷模型示意图Fig.6 Three kinds of experimental targets and the schematic diagrams of them IBP 算法、PSM 算法和FDMF 算法对实验目标A的成像结果在xoy平面、xoz平面和yoz平面上的最大值投影(Maximum Projection,MP)分别如图7~图9所示。将3种算法的成像结果与实验目标A 的结构示意图进行对比可以发现,3种算法均能对PTFE 块的前后表面及其内部嵌入的锡箔条正确成像。进一步比较IBP 算法、PSM 算法和FDMF 算法的成像结果,可以看出FDMF 算法可以获得与IBP 算法、PSM算法相似的成像效果,3 种算法对不同深度的锡箔条成像质量几乎相同,这进一步验证所提的FDMF算法可以对介质中不同深度的嵌入型缺陷进行成像。 图8 PSM算法对目标A 3D成像结果的最大值投影图Fig.8 MP of the 3D imaging result of target A by PSM algorithm 图9 FDMF算法对目标A 3D成像结果的最大值投影图Fig.9 MP of the 3D imaging result of target A by FDMF algorithm 实验目标B 为一个内嵌复杂金属目标的PTFE块,如图6(b)所示,该模型主要用于模拟内嵌复杂缺陷的介质目标,以验证算法对介质中复杂散射目标的成像能力。实验目标B 的PTFE 块长宽厚尺寸分别为20 cm、20 cm 和2.5 cm,内嵌的复杂金属目标为一个金属“柠檬片”,内嵌于PTFE 块中y=-2 cm 的平面内,如图6(e)所示,金属“柠檬片”的半径为6 cm,厚度为0.2 cm。 IBP 算法、PSM 算法和FDMF 算法对实验目标B的成像结果在xoy平面、xoz平面和yoz平面上的最大值投影分别如图10~图12所示。将3种算法的成像结果与实验目标B 的结构示意图进行对照,可以发现3 种算法均能对PTFE 块的前后表面及其内嵌的金属“柠檬片”正确成像,且金属“柠檬片”的位置正确,内部细节充分,进一步说明3种算法均具备对介质目标内部的复杂散射目标进行成像的能力。将FDMF 算法与IBP 算法、PSM 算法的成像结果进行相互对比可以发现,3 种算法的成像效果仍然类似,进一步说明FDMF 算法在对介质内嵌的复杂目标进行成像时,具备与IBP算法、PSM 算法相同的成像性能。 图10 IBP算法对目标B成像结果的最大值投影图Fig.10 MP of the 3D imaging result of target B by IBP algorithm 图11 PSM算法对目标B成像结果的最大值投影图Fig.11 MP of the 3D imaging result of target B by PSM algorithm 图12 FDMF算法对目标B成像结果的最大值投影图Fig.12 MP of the 3D imaging result of target B by FDMF algorithm 空腔是介质目标的常见缺陷类型之一。实验目标C 为一个内含4个大小不同空腔的PTFE 块,如图6(c)所示,该模型用于模拟含有空腔型缺陷的介质目标,以检验FDMF 算法对介质内部空腔的成像能力。该PTFE 块的长宽厚尺寸分别为20 cm、20 cm 和8 cm,四个空腔的位置分布如图6(f)所示,其中空腔1是一个半径为2 cm、厚为4 cm的圆柱体,与PTFE块的前表面距离为2 cm;空腔2是一个长宽厚分别为3 cm、2 cm、3 cm的长方体,与PTFE块的前表面距离为3 cm;空腔3是一个长宽厚分别为3 cm、2 cm、2 cm 的长方体,与PTFE 块的前表面距离为4 cm;空腔4 是一个长宽厚分别为2 cm、2 cm、1 cm的长方体,与PTFE块的前表面距离为5 cm。 为了更清晰地观察目标C 中空腔的成像情况,我们选取目标C 的3D 成像结果在y=0 m、y=-0.02 m、y=-0.08 m 等3 个平面上的切面图进行比较。其中,第一个切面为目标C 成像结果在平面y=0 m 上的切面图,该切面为目标C 前表面所在平面,IBP 算法、PSM 算法和FDMF 算法对该面的成像结果分别如图13(a)~图15(a)所示,从成像结果来看3种算法的成像结果几乎没有差异。第二个切面为目标C成像结果在平面y=-0.02 m上的切面,也是空腔1 前表面所在的平面,3 种算法对该面的成像结果分别如图13(b)~图15(b)所示,在3 种算法成像结果的切面图中均能观察到空腔1 的前表面,但还能观察到空腔2 前表面成像结果的旁瓣,对比图13(b)~图15(b)可以发现,IBP算法成像结果中空腔2 前表面成像结果的旁瓣更重,而PSM 算法和FDMF 算法中空腔2 前表面成像结果的旁瓣更弱,分析其主要原因在于IBP算法是一种成像几何敏感的算法,但在成像实验中目标C 的前表面无法完全与阵列雷达所在平面平行,导致成像过程中计算出的电磁波折射点与实际折射点并不完全一致,造成成像结果出现一些散焦。第三个切面为目标C成像结果在平面y=-0.08 m 上的切面,该平面为目标C后表面所在的平面,其成像结果分别如图13(c)~图15(c)所示,在该表面的成像结果中,不仅可以观察到目标C 后表面的成像结果,还可以观察到目标C 中4 个空腔的轮廓,出现该现象的主要原因是由于目标C 中的空腔会多次散射电磁波,目标C 后表面上4 个空腔正对的部分散射电磁波较弱,导致对应位置成像结果较弱而体现为轮廓。总的来说,对比3 种算法的成像结果,可以验证FDMF 算法在对介质内嵌的空腔进行成像时,具备与IBP 算法、PSM算法相同的成像性能。 图13 IBP算法对目标C成像结果的切面图Fig.13 Sections of the 3D imaging of the target C by IBP algorithm 图14 PSM算法对目标C成像结果的切面图Fig.14 Sections of the 3D imaging of the target C by PSM algorithm 图15 FDMF算法对目标C成像结果的切面图Fig.15 Sections of the 3D imaging of the target C by FDMF algorithm 本文提出了一种基于匹配滤波的分层介质目标3D 成像算法,该算法将雷达回波变换至频域进行成像处理。与同样适用于分层介质目标成像的典型时域算法IBP 算法相比,所提的FDMF 算法利用电磁波沿介质分界面的波数分量将保持连续的性质,避免了电磁波在介质分界面上折射点的计算,从而显著降低了算法的计算量,提高了成像效率;而与频域算法PSM 算法相比,由于FDMF 算法可以通过矩阵乘法进行实现,其在成像速度上仍具备一定优势。数值仿真结果验证了这一结论。同时,本文还利用矢量网络分析仪和扫描架搭建了成像实验系统,开展了实验测试,通过对三种不同类型的目标进行测量成像,进一步验证了所提算法对介质中不同深度目标、介质中内嵌的复杂目标及介质内部空腔等不同类型缺陷的成像能力。这将为介质目标的快速成像研究提供一定支撑。

4 实验结果与分析










5 结论

