基于原点矩偏导的K分布杂波参数估计
杨立儒 刘永祥 杨 威 沈亲沐
(国防科技大学电子科学学院,湖南长沙 410073)
1 引言
恒虚警检测(Constant False Alarm Rate,CFAR)[1]和雷达杂波分类[2]时,需要准确估计出杂波数据分布模型的参数,较大的估计误差会导致检测和分类的性能下降。目前常用来描述和分析杂波幅度分布的模型主要有韦布尔分布、对数正态分布、瑞利分布和K 分布等[3]。对于以上分布,参数估计方法最准确的是最大似然估计法[4],但是最大似然估计受限于待估计参数的解析形式,当解析形式复杂时通常求解困难或计算量大,如K 分布的最大似然估计法[5]。而矩估计方法[6]因其计算量小,克服了基于最大似然估计方法计算量大的缺点。但是,当观测序列的长度受限时,K 分布的高阶矩估计法计算会出现偏差,导致计算出的形状参数v<0,如二阶/四阶矩估计法[7]、二阶/分数阶矩估计法[8]、log-Ⅲ型估计法[9]等都存在这种估计偏差。文献[10]针对噪声条件下的K 分布参数估计问题,分别提出了一种一/二/三阶矩估计法和神经网络估计法,但前者估计有效率并不理想且常出现异常估计值,后者需要大量数据进行训练。
本文针对该问题,在矩估计方法的基础上,通过推导原点矩偏导与原点矩之间的关系,提出了一种新的有效的基于矩估计偏导的参数估计方法。这种方法对数据长度受限造成的偏差较小,能够有效避免计算出形状参数v<0 的情况出现。通过仿真和实测杂波数据处理,与常用K 分布的矩估计方法进行比较,验证了本方法的准确性和有效性。
2 基于原点矩偏导的K 分布杂波参数估计方法
K分布的概率密度函数为[11]:

式中,v表示形状参数,取值范围为0 K分布的原点矩(k>0)为: 矩估计方法通常为了求解形状参数v和尺度参数σ,通过选择两个不同的原点矩阶数k,得到两个关于v、σ和原点矩的关系式,然后联立关系式求解出v和σ的值。这些方法是在两个不同阶数k的条件下进行求解,通过不同阶数的矩估计值代替理论值以求解形状参数v,极可能会放大近似误差。比如二阶/四阶矩估计法中,形状参数v使用了二阶矩和四阶矩的近似值和,具体如式(3)所示,其中的近似计算极可能放大形状参数v的估计误差,甚至可能出现v<0的情况。 大量实测数据也表明,当数据长度有限或者存在噪声的影响,在二阶/四阶矩估计法中,当<2时会出现部分样本计算出v<0的情况,使用二阶/分数阶矩估计法、log-Ⅲ型估计法等方法同样也会出现v<0 的异常值。对于出现v<0 的异常值情况,文献[12]采用了剔除异常样本的处理办法。 针对上述问题,通过分析原点矩表达式的特点,推导提出一种基于原点矩偏导的K 分布参数估计方法,该方法仅利用单个k阶原点矩,避免了需要多个原点矩的近似值参与运算,不仅能提升形状参数的估计有效率,而且有望提高形状和尺度参数的估计精度。具体推导过程如下,令 将k看作变量,分别对G(k)和E[zk]求偏导,可得式(6)和式(7): 又因为伽玛函数有以下性质 其中,ψ(•)是digamma函数,即普西函数(psi function),则式(6)进一步求解,可以得到式(9)。 将式(9)代入式(7),可得 因此,联立式(10)和式(11)可得式(12)。 分析式(2)发现,对E[zk]取对数同样可以得到ln(2σ)项,即 因此,联立式(12)和式(13)可得 当k的值给定后,式(14)就是关于形状参数v的方程,其是由单个k阶原点矩推导得到,避免了不同阶原点矩的求解。进一步,式(14)还可表示为 公式(15)左侧部分是待求变量v的函数,令 当v>0时,f(v)是单调减函数,证明如下。 证明 普西函数的级数表达式 其中,γ为欧拉常数。 将普西函数的级数表达式代入式(18)并整理得 因此,式(15)通过数值计算求解方程可以得到形状参数v的唯一解。利用式(2),不难推导得出尺度参数估计式,如式(20)所示。将估计的形状参数带入式(20)即可得尺度参数σ的估计值。 由式(15)和式(20)可以看出,本文方法形状参数v和尺度参数σ是通过单个k阶原点矩求解得到,相当于在同一标尺下计算形状参数v和尺度参数σ,避免了需要两个不同阶原点矩的近似值参与运算,进而可以避免不同阶原点矩联合计算造成估计误差的放大,因此能提高估计的性能。 本部分对所提参数估计方法的有效率和估计精度进行了实验分析,然后对比了不同估计方法对杂波数据的尾部拟合情况,最后分析了噪声对参数估计方法的影响。 首先使用仿真数据验证本文方法的估计有效率和估计精度。因为服从K 分布的杂波形状参数通常在0.1~10之间变化[16],本文实验定义仿真参数v取值为[0.5∶0.5∶10],σ取值服从均匀分布U~(0,5),利用零记忆非线性(Zero-memory Non-linear,ZMNL)方法[17]分别进行1000次仿真,随机生成长度256 点的K 分布数据(长度受限)。采用常用的矩估计方法,如二阶/分数阶矩估计法、log-Ⅲ型估计法、二阶/四阶矩估计法、log(z)的一二阶矩估计法[13]、基于zrlog(z)期望估计法[18]、基于zlog(z)期望估计法[19]和本文方法进行参数估计,当仿真参数v=3,原点矩阶数k=0.5 时,7 种方法的估计有效率ρ和估计精度MSD的统计情况如表1所示。 表1 可以看出,当仿真参数v=3 时,文献[13]、文献[18]和本文方法估计有效率为100%,但是估计精度比本文方法要差。表1 中MSD 的统计结果是经过剔除掉无效估计样本后进行的统计。 表1 v=3时估计有效率和估计精度统计情况Tab.1 Statistics of estimation efficiency and estimation accuracy when v=3 对100%估计有效率的方法做1000个样本的估计精度统计,表2所示。 尽管三种方法的估计有效率都为100%,但是表2表明了本文方法的估计精度更高。七种方法的无效估计次数与仿真参数v之间的关系如图1所示。 表2 v=3时1000个样本的估计精度统计情况Tab.2 Statistics of estimation accuracy of 1000 samples when v=3 图1 可以看出,当仿真参数v小于等于2 时,所有方法的无效估计次数都为0。随着v的增加,二阶/分数阶估计法、log-Ⅲ型估计法、二阶/四阶矩估计法、文献[19]方法的无效估计次数也在不断增多,文献[13]、文献[18]方法和本文方法的无效估计次数依然为0。 图1 各方法估计有效率与仿真参数v之间的关系Fig.1 Relationship between estimation efficiency and simulation parameter v of each methods 仿真参数v=3时,文献[18]和本文方法中都存在阶数k,当k的取值为[0.1∶0.1∶5]时,估计有效率ρ都能达到100%,但是本文方法的估计精度更高,k与估计精度MSD之间的关系如图2所示。 本文方法中,当k=0.2时MSD最小,为1.8955×10-3。当k>0.9时,随着k的增加MSD也会增加,当k=0.7时,部分仿真样本使用文献[18]方法开始出现非正常运算产生的奇异值NaN,当k越大出现奇异值的样本越多。使用文献[18]方法出现NaN的数量比使用本文方法的数量多,如k=5 时,1000 个样本中使用文献[18]方法出现奇异值69个,本文方法25个。出现NaN是因为随着k的增大,部分样本估计出的v会出现比较大的情况,甚至大于100,而gamma(100)是个非常大的数,导致容易出现Inf/Inf 的情况。图2中,k>0.6时的MSD 值是剔除掉出现奇异值样本的统计结果,k越大需要剔除的样本越多。 图2 仿真数据实验的阶数k与MSD之间的关系Fig.2 Relationship between order v and MSD in simulation data experiment 累积分布函数(Cumulative Distribution Function,CDF)[20]能描述随机变量的统计规律,可以对K 分布的尾部情况进行描述。对仿真参数v=3,σ=1,样本长度256 点的1000 组仿真数据使用CDF 进一步验证各方法对K 分布拖尾部分的拟合情况。图3是各方法与仿真数据的尾部拟合情况。CDF 拟合结果来看,除了文献[13]方法在尾部拟合效果较差外,其他方法在尾部拟合的都很好。总体而言,文献[13]方法性能最差,其次为二阶/四阶估计法、文献[18]方法、log-Ⅲ型估计法和文献[19]方法、二阶/分数阶矩估计法,本文方法性能最佳。 图3 K分布的尾部拟合情况Fig.3 The tail fitting in the K-distribution simulated data 当K 分布在有噪声影响的情况下,传统矩估计方法模型已不适用,需要对矩估计模型进行修正。 这里用估计量的相对偏差|-v|/v表示尺度参数估计的精度。对仿真参数v=2,σ=2.2,杂噪比分别为CNR=30 和CNR=10,样本长度为256 点的1000组仿真数据进行分析,各方法的平均相对偏差如表3和表4所示。 表3 有30 dB杂噪比的平均相对偏差统计情况Tab.3 Statistics of average relative deviation with 30 dB CNR 表4 有10 dB杂噪比的平均相对偏差统计情况Tab.4 Statistics of average relative deviation with 10 dB CNR 在有噪声的情况下,文献[18]方法和本文方法的估计有效率都为100%,但是本文方法的平均相对偏差和估计方差最小。文献[10]方法对数据敏感,部分样本的估计值特别大甚至达到106级别,导致平均相对偏差和估计方差都很大。将文献[10]方法估计出v>100 的样本剔除,文献[10]方法的估计精度有所提升,证明了文献[10]方法对数据的敏感性。文献[10]中的矩估计方法因为存在高阶矩的原因,矩估计结果会出现特别大的v值,对数据要求较高。基于原点矩偏导的估计方法不会出现v<0的情况,并且偏差比传统矩估计方法的估计偏差小,估计方差也是最小的。 在没有噪声影响的情况下,使用仿真参数v=2,样本长度256点的1000组仿真数据进行分析,各方法的平均相对偏差如表5所示。在理想无噪声条件下,本文方法性能仍然优于所比较的现有方法。 表5 无噪声的平均相对偏差统计情况Tab.5 Statistics of average relative deviation without noise 实验结果表明,当K 分布杂波中含有噪声时,本文方法的性能超过其他方法的性能,但是估计结果的平均相对偏差仍然较大,下一步需要对杂波模型进行修正;当K 分布杂波中不含有噪声时,杂波的噪声修正模型不适用且对数据敏感,本文方法的性能同样超过其他方法的性能。以上数据分析表明了,相较于其他矩估计方法,本文方法的鲁棒性相对更好。 为进一步验证本文方法的有效性,实测数据采用IPIX 雷达1998 年测量的数据[21],数据形式为复数形式,包含I 通道和Q 通道,脉冲重复频率为1 kHz。IPIX 数据在加拿大格里姆斯比市安大略湖岸边采集得到,包含不同日期不同时间不同气象条件下的湖面回波。对160 组不同距离单元,长度为256 点数据取模进行分析,分别进行不同方法的参数估计,估计有效率ρ如表6所示。 表6 可以看出,所有方法的估计有效率都为100%,本文方法(k=0.5 阶)的估计精度是最高的。文献[13]方法出现6个样本计算出异常均方差(v的估计值大于100),文献[18]方法出现4 个样本计算出异常均方差。表6 中MSD 的统计结果是经过剔除掉异常均方差后进行的统计。 表6 实测数据估计有效率和估计精度统计情况Tab.6 Statistics of estimation efficiency and estimation accuracy in measured data 实测数据中,当k的取值为[0.1∶0.1∶5]时,文献[18]和本文方法估计有效率ρ依然能达到100%,但是本文方法的估计精度更高,k与MSD 之间的关系如图4所示。 本文方法中,当k=0.3时MSD最小,为6.7876×10-3;当k>0.9 时,随着k的增加MSD 也会增加;当k=0.7时,部分仿真样本使用文献[18]方法开始出现非正常运算产生的奇异值NaN,当k越大出现奇异值的样本越多。使用文献[18]方法出现NaN 的数量比使用本文方法的数量多,如k=5 时,1000 个样本中使用文献[18]方法出现奇异值62个,本文方法23 个。图4 是剔除掉出现奇异值样本的MSD 统计结果。 图4 实测数据实验的阶数k与MSD之间的关系Fig.4 Relationship between experimental order v and MSD in measured data 通过实验分析,当使用原点矩进行K 分布的参数估计时,阶数k的取值较小时能得到较为理想的估计结果和精度,这一结论与文献[22]相同。文献[22]指出,K 分布的参数估计中高阶矩对数据较为敏感,应尽量选取低阶矩。二阶/四阶矩估计法、二阶/分数阶矩估计法、log-Ⅲ型估计法、log(z)的一二阶矩估计法、基于zrlog(z)期望估计法和基于zlog(z)期望估计法等方法都有高阶矩(k≥1)的使用,并且以上方法为了求解方便,使用了不同的阶数k进行联立方程求解,造成计算误差的扩大,本文方法的推导是基于单个阶数k,所以计算误差最小。 本文提出基于原点矩偏导的K 分布杂波参数估计方法,避免了常规矩估计方法在处理杂波数据时会导致出现部分错误参数估计的问题。利用该方法对仿真和实测的K 分布数据进行了参数估计,结果表明该方法具有100%的估计有效率和最小的均方误差。通过实验分析,当使用原点矩进行K 分布的参数估计时,阶数k的取值较小时能得到较为理想的估计结果和精度。通过选取合适的阶数k,可以提升观测序列长度受限的K 分布杂波参数估计结果和精度,进而提升检测器和分类器的性能。
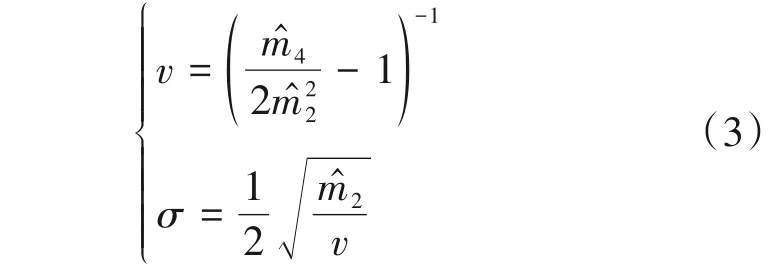














3 参数估计的有效率和估计精度分析
3.1 估计有效率和估计精度分析




3.2 尾部拟合情况分析

3.3 噪声对模型影响分析



4 IPIX海杂波实测数据分析


5 结论

