基于无网格压缩感知的雷达通信一体化系统目标参数估计方法研究

刘飞峰 刘鸿杰 缪颖杰 李 浩 胡 程

（1.北京理工大学信息与电子学院雷达技术研究所，北京 100081；2.卫星导航电子信息技术教育部重点实验室（北京理工大学），北京 100081）

1 引言

传统应用场景中，雷达与通信设备分别占用不同的硬件平台与频谱资源，这种分立式的设计会导致电子系统的体积、功耗以及成本增加，恶化了电磁环境，容易造成电磁频谱拥挤与干扰等诸多问题。鉴于此，雷达通信一体化设计可以让雷达与通信共享硬件平台，系统综合化、集成化、小型化程度更高，可更高效地利用频谱资源，从而解决上述难题［1-2］。

正交频分复用（Orthogonal Frequency Division Multiplexing，OFDM）是一种多载频调制的波形，凭借其高维度、高通信速率、强抗干扰能力等优势得到了广泛的关注，被广泛用于一体化波形设计中，Sturm 等人研究了OFDM 在车载雷达通信中的应用，可实现平台间通信，并通过傅里叶变换处理实现目标测速测距［3］；Oziewicz 通过MUSIC 的方法实现了OFDM 信号多径时延估计［4］。刘永军等人采用子空间投影方法实现对目标的距离与速度估计［5］，此方法性能优于传统傅里叶变换方法，但是其性能依然受噪声影响大，难以保证低信噪比下的探测性能。

近些年来，压缩感知技术被广泛应用在信号处理领域，Sen 等人利用稀疏恢复理论实现OFDM 信号对目标距离和多普勒的估计，但运算量较大，且估计精度受限于网格估计［6］；为克服以上难题，一种称为原子范数最小化（Atomic Norm Minimization，ANM）的无网格压缩感知技术被提出，该方法将优化问题凸优化为一个半正定规划（Semi-definite Pro⁃gramming，SDP）问题［7-8］，并构建半正定Toeplitz 矩阵，通过对此矩阵的范德蒙分解得到恢复的信号以实现超分辨，可有效避免网格失配的问题。付卫红等人利用原子范数最小化的方法实现了多跳频信号的时频估计［9］，而OFDM 信号本身具有的多载频特点，为基于原子范数时频估计提供了可能。Zheng 等人基于OFDM 被动雷达系统，利用原子范数实现了目标的时频估计［10］，但是方法前提需要直达波进行通信解码，而解码中产生的误码会恶化目标时频估计性能。鉴于此，本文利用OFDM 信号作为雷达通信一体化波形，其作为探测波形使用时，通信码元是已知的，因此不会出现上述性能恶化现象，并在此基础上引入核范数最小化（Nuclear Norm Minimization，NNM）、迹范数最小化（Trace Norm Minimization，TNM）等衍生优化问题，实现了多目标时频二维联合估计，并针对不同优化问题进行分析［11］。此外，为减轻二维联合估计带来的繁重的计算压力，采用解耦原子范数最小化（Decoupled Atomic Norm Minimization，DANM）［12］将二维估计问题转换为两个一维估计问题，在维持原子范数优良估计性能的基础上极大的减小了运算量，为高通道数信号模型提供快速求解可能。除此之外，本文还提供了各类估计方法的多测量矢量（Multiple Mea⁃surement Vector，MMV）模型，可有效解决低信噪比下求解精度差、恢复成果率低的问题。

2 信号建模

雷达单脉冲发射的第m个符号的OFDM 信号复包络表达式为：

其中am(n)为第m个符号、第n个子载波的幅度相位调制符号，其中T=Tcp+Tp表示信号时宽，Tp为OFDM 有效时长，Tcp为单OFDM 符号循环前缀长度，N为子载波数目，子载频间隔Δf=1/Tp，带宽B满足：B=NΔf。

多符号OFDM信号复包络可建模为：

其中M为符号个数。

发射信号经过多目标反射后的基带回波信号可表示为：

其中，K表示目标数量，第k条路径上的时延和多普勒频率分别表示为fk和τk。复数系数Ak用于表示其路径衰减，ω(t)表示高斯白噪声。

通常来说，OFDM 波形在无线通信使用中会加入循环前缀来消除多径对符号间串扰的影响，OFDM 雷达通信一体化波形同样可以利用循环前缀技术保证不同路径的回波可在同一个符号内，由于OFDM 子载波在频域是正交的，且在不同符号间是时分的，同时发射的通信信息是已知的，那么接收机采样得到回波信号经过去循环前缀处理后的第m个符号可更简洁的表示为：

对第m个块中的接收信号进行傅里叶变换，那么第n个子载波中的信号可以表示为：

考虑单快拍情况，上述公式可化简为：

则接收信号可进一步表示为如下导向矢量：

其中⊗表示克罗内克积。

3 基于无网格的目标多参数估计

3.1 基于矢量的无网格多参数估计

传统的压缩感知算法，其精度受限于网格精度，会出现字典失配等问题，对估计精度产生一定的影响。因此可以考虑使用无网格估计方法。

将信号模型构建为如公式（7）所示的MN×1 维导向矢量的形式，定义原子集如下

此集合可以理解为是类似于压缩感知中的字典，但其是无限精度的，z是该原子集中k个原子的线性组合。

sk为任意的复系数，C 表示复数集。当对应所用原子数最少即对应最小l0原子范数时，此时求得的解‖z‖Α，0即为最优解。但此问题为NP-hard问题，无法对其直接进行求解，［13］证明向量z的l0范数最小化可等价为矩阵秩的最小化问题：

其中x是一个待优化的变量。但此问题是非凸的，无法直接求解，因此可将l0原子范数进行如下凸近似松弛，考虑目标在时频域的稀疏性，其原子范数可表示为：

信号向量及其子空间可以通过上述原子范数的最小化估计获得：

将上述问题转换为如下半正定问题，即可得到其原子范数最小化的表达形式［14］：

其中λ为正则化参数，用于平衡拟合误差和原子范数项，S(T) ∈CMN×MN为待估计的Block Toeplitz 矩阵，其非零子空间编码了目标信息，可看作为由信号估计导向向量所构成的协方差矩阵，其表达式为：

此外，针对不同的凸近似方法，其优化问题可有不同的形式，矩阵秩的最紧凸松弛为核范数［15］，那么考虑多快拍情况下，公式（10）的凸优化问题可转换为如下核范数最小化优化问题，表达形式为：

核范数最小化优化估计问题的多快拍表达形式为：

其同样可理解为问题（10）的凸近似，多快拍表达形式为：

STNM(T) ∈CMN×MN为基于迹范数最小化凸优化问题的待估计Block Toeplitz矩阵。

上述基于ANM、NNM、TNM 的三种估计问题均可由CVX 工具箱进行求解，之后对估计得到的半正定矩阵S(T)进行特征值分解S(T)=UΛUH后可得其相应的估计协方差矩阵：

对估计协方差矩阵做特征值分解可得到其噪声子空间En，之后使用如下二维谱估计即可得到信号的时频估计结果。

其中ϕ∈[0，1]，ϑ∈[ -0.5，0.5 ]，之后对二维谱进行峰值搜索，寻找K个最大峰值即可得到目标时频估计结果。

3.2 基于解耦原子范数最小化的多参数估计

由于上述二维估计方法基于矢量的克罗内克积，当通道数较大时，所估计S(u)的维度会大幅增加，其运算量会成倍增加，难以适应高通道数场合，为解决此问题，引入解耦原子范数的概念，即将优化问题的矢量形式克罗内克积运算改为如下的形式：

此时zDANM∈CN×M可表示为两个向量的互协方差矩阵。

那么解耦原子范数的最小化估计问题为：

此估计方法将二维估计问题解耦为两个一维估计问题，其中Tb(ub)与Ta(ua)分别表示与b(ϑk)和a(ϕk)相关的Toeplitz 矩阵，分别由其第一行复向量ub与ua构成。ua(0)与ub(0)分别表示Tb(ub)与Ta(ua)矩阵主对角线的第一个元素。分别对两个矩阵做范德蒙分解即可得到时延、频率估计结果。之后利用最大相干配对方法进行时频配对，得到时频估计结果，即：

此方法将一个MN×MN的半正定矩阵优化问题转化为（M+N）×（M+N）的优化问题，极大地减少了计算量。

3.3 计算量分析

本节针对上述ANM、NNM、TNM 以及DANM 四种估计模型进行计算量分析。为保证求解精度，本文采用基于内点法［16］的SDPT3 作为求解器进行求解，其每次迭代的时间复杂度为O(U3)，迭代次数最多为，其中，U表示SDP 模型约束中的半正定矩阵的大小，ε表示恢复精度。因此，总的时间复杂度为O(U3.5log(1/ε))。对于ANM、NNM、TNM 等基于矢量化的无网格估计问题有U=MN，而DANM 将求解问题变成两个低维Toeplitz 矩阵的估计问题，因而有U=M+N。在SDP 求解过程后，可对求解得到的Toeplitz 矩阵进行范德蒙分解来检索所有的频率分量。而对于ANM、NNM、TNM 基于矢量化的无网格稀疏恢复方法，其需要进行范德蒙分解的计算复杂度为O(M2N2L)，其中L表示Toeplitz矩阵的秩，而对于DANM 方法，其仅需做两个低维的范德蒙分解即可完成问题求解，计算复杂度为O(N2+M2)。显然可以看出，DANM 方法的运算复杂度是远小于ANM、NNM、TNM 等估计方法的。上述四种估计方法的SDP 求解与范德蒙分解复杂度之和详见表1。

表1 复杂度分析Tab.1 Complexity Analysis

4 仿真结果与分析

为了验证本文原子范数方法的有效性，本节开展典型系统的计算机仿真工作，对所建模型与所提估计方法进行仿真验证。仿真中所采用的系统参数如表2所示。

表2 仿真参数Tab.2 Simulation parameters

采用均方根误差作为性能评价标准，目标归一化多普勒估计精度由下式计算：

目标归一化时延估计精度由下式计算：

其中K为目标个数，MC 为蒙特卡洛次数。基于以上系统参数开展建模与算法仿真，不同场景下的仿真结果如下。

4.1 无杂波场景仿真

假设场景中仅存在目标，假定目标的真实速度分别为：vreal=[ ]-90 m/s，60 m/s，72 m/s，真实距离分别为：dreal=[1.5 km，4.5 km，4.8 km]，目标信噪比均为15 dB，其二维时频仿真结果见图1所示。

图1 存在相邻目标二维时延多普勒估计结果Fig.1 Two-dimensional delay-frequency estimation results with adjacent targets

图1 结果表明MUSIC 算法的谱估计性能相较其他方法差，二维估计谱存在旁瓣，且对于存在相邻目标的场景，其相邻多目标分辨能力较差；CS-L1范数为基于网格的估计算法，其估计结果存在少量伪峰，容易造成虚警现象，且其估计结果受限于网格精度，并不能实现高精度估计。而ANM、NNM、TNM 结果近似，除了目标谱外无明显噪底，且由于此类估计基于信号在时频谱上的稀疏性，其天然具有相邻多目标分辨能力，虽然其分辨能力同样受限于通道数目，但是性能仍是优于传统谱估计算法。DANM 是基于原子范数的改进，其估计结果与其他三种无网格估计问题近似，但有着更小的计算量，意味着其可应用在高通道数的场合。

4.2 存在杂波场景仿真

假定照射场景存在少量强反射静止杂波，其距离设定为：[1.5 km，2.25 km，3.75 km，4.5 km，5.25 km，6 km，6.75 km ]，速度均为0 m/s，且杂噪比均设置为10 dB；目标的速度与距离分别设置为：vreal=[ -90 m/s，60 m/s ]，dreal=[1.5 km，4.5 km]，信噪比均设置为10 dB，其二维时频仿真结果如图2所示。其中MUSIC 算法与CS-L1 算法估计结果与目标真实时频出现偏差，估计性能较差，但基于无网格稀疏恢复的各类估计算法可完美恢复出目标与杂波的时频谱，验证了基于原子范数最小化的各类范数的多目标时频谱估计能力。

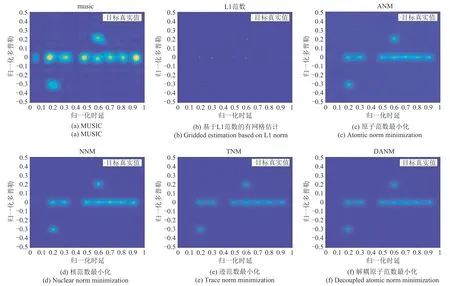
图2 杂波场景二维时延多普勒估计结果Fig.2 Two-dimensional delay-frequency estimation results of clutter scene

4.3 多快拍处理仿真

上述两节仿真结果说明了无网格稀疏恢复相较于传统估计算法的性能优势。无网格稀疏恢复方法在信噪比较低的情况下，可通过增加快拍数提高估计性能。本小节假定目标数量为3 个，其真实速度分别为：vreal=[ ]-90 m/s，-60 m/s，72 m/s，真实距离分别为：dreal=[1.5 km，4.5 km，4.8 km]，信噪比均为0 dB，图3为ANM、NNM、TNM 以及DANM 估计的仿真结果，其结果表明了低信噪比下噪声对基于原子范数等估计方法的估计结果影响较大，使得目标点估计结果与真实值存在偏差，时频估计精度恶化。

图3 0 dB信噪比下的时延多普勒估计结果（单快拍）Fig.3 Delay-Doppler estimation results under 0 dB SNR（SMV）

为降低噪声对时频估计性能的影响，采用多快拍（MMV）提高ANM、TNM、NMM、DANM 估计的估计性能，图4 与图5 为L分别取值为3、30 时的估计结果。随着L的增大，估计性能在逐渐提高，目标时频估计更接近真实值。L取值30 时，根据图5所示，算法估计的结果与真实值几乎一致，验证了多快拍的降噪特性。因此，在低信噪比情况下，可通过多快拍处理实现以上方法的高精度目标时延多普勒估计。

图4 0 dB信噪比下的二维时延多普勒估计结果（多快拍，L=3）Fig.4 Delay-Doppler estimation results under 0 dB SNR（MMV，L=3）

图5 0 dB信噪比下的时延多普勒估计结果（多快拍，L=30）Fig.5 Delay-Doppler estimation results under 0 dB SNR（MMV，L=30）

4.4 性能仿真

本节采用蒙特卡洛对不同信噪比条件下各估计方法的时频估计性能进行仿真，使用均方根误差（RMSE）作为算法性能评价标准，横轴为信噪比，取值为-5 dB～25 dB，以5 dB 为间隔，蒙特卡洛次数为100次，且本次仿真场景仅考虑目标场景，两目标的真实速度为：vreal=[ -90 m/s，60 m/s ]，真实距离为：dreal=[1.5 km，4.5 km]，其他仿真参数见表2。图6与图7 分别表示归一化时延估计RMSE 与归一化频率估计RMSE随信噪比变化的曲线。

图6 不同估计方法归一化时延估计RMSE仿真实验结果Fig.6 RMSE simulation results of normalized delay estimation with different methods

图7 不同估计方法归一化多普勒估计RMSE仿真实验结果Fig.7 RMSE simulation results of normalized Doppler estimation with different methods

仿真结果表明，ANM、NNM、TNM、DANM 基于无网格的估计方法有着更高的估计精度，证明该类算法有着更好的降噪性能，算法的估计性能也是相近的，估计结果的RMSE 随信噪比的增加呈现下降趋势。但是DANM 的运算量更小，意味着更少的运行时间。图6 与图7 为基于单快拍进行的仿真实验，图8 与图9 分别为不同快拍数下ANM、NNM、TNM、DANM 四种估计方法在不同信噪比下的时频估计精度结果，仿真结果表明快拍数取值为L=30时四类方法的估计精度明显优于单快拍下的估计精度结果，且对于信噪比取值为-5 dB 的情况，其估计性能改善尤为明显，实际应用中可适当增加快拍数以提高估计精度。

图8 不同快拍数下归一化时延估计RMSE仿真实验结果Fig.8 Simulation results of normalized delay estimation RMSE under different snapshot numbers

图9 不同快拍数下归一化多普勒估计RMSE仿真实验结果Fig.9 Simulation results of normalized Doppler estimation RMSE under different snapshot numbers

5 结论

本文利用OFDM一体化信号多符号多子载波的特性，提出一种可用于一体化波形的高精度二维时频估计算法。针对不同的凸近似方法，提供了ANM、NNM、TNM 等基于矢量的无网格压缩感知估计问题模型，并采用解耦原子范数的方法以解决其运算量较大的问题。仿真结果表明，DANM可在保留原子范数高精度估计性能与鲁棒性的同时，将计算负荷减少几个数量级，其应用场景可以扩展到高维谱估计问题。未来的工作会对数据压缩情况下进行性能分析。