解一题,通一法——以一道圆锥曲线模考题求解为例

浙江省湖州中学(313000) 祝峰泽浙江省湖州市滨湖高级中学 (313000) 郑梦华

圆锥曲线是高中数学的重要内容,蝴蝶型斜率问题是圆锥曲线的一个重要考点,这一类题型对学生数学运算、逻辑推理等素养要求较高,并且对圆锥曲线的研究方法、研究工具及学会自主探究发现圆锥曲线的一般定义及通性通法显得尤为重要.本文以2023届广州期末卷第21题为例,探究其多解、优解及通解的规律,从而发现圆锥曲线的一般性质.

1 试题呈现

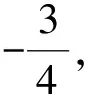
2 解法探究

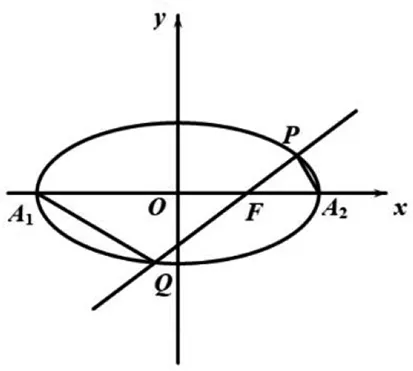
图1

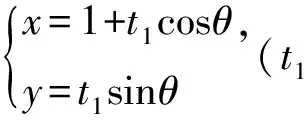
评注:解法一较常规,设直线方程后,联立椭圆方程,将斜率的比值转化为代数后利用韦达定理进行计算即可;解法二从点出发,得到直线方程后,求得另一点的坐标,该解法计算较大;解法三运用直线上三点共线斜率相等,将斜率问题转化为纯代数问题,最后解方程组即可,对思维能力要求较高;解法四运用参数方程方法,计算量减少,较为抽象.

图2

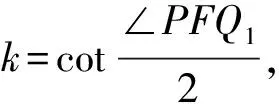
评注:第二问主要考查三角形面积求法、斜率的几何意义、基本不等式等,难度较大.除上述方法外,也可以考虑求点到直线的距离,从而求出三角形面积;还可以运用参数方程求解.

3 试题推广

上述推广1及推广2的证明同本文试题第一问解法一,此略.双曲线也有这两类似的性质.

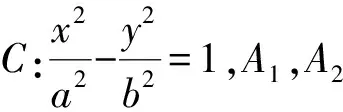
综合上述推广,又可将其性质从逆思考方向予以探究,相应得到其逆命题.

张景中院士认为:小巧一题一法,固不应提倡,大巧法无定法,也确实太难,出路在于中巧.中巧即数学解题中有章可循的通性通法,教师在教学中可以帮助学生归纳总结得到一类问题的通性通法,在此基础上,学生能够学会举一反三并形成系统性的解题策略,由此发展学生的数学解题能力.