一道二元函数最值问题的多视角探究

安徽省肥东城关中学 (231600) 王东海

最值问题是高中数学的核心内容，往往需要熟练掌握多种解题思想方法，是高考考查的重点、热点内容.最值问题在选择题、填空题与解答题中均可灵活命制，有时可单独命题，有时在解析几何题中命制求几何量、代数式的最值问题，有时在三角函数题中命制求面积、周长等的最值问题.如何提高学生求解最值问题的能力一直困扰着一线教师.本文以一道最值问题为例，进行多角度探究.

1 试题再现

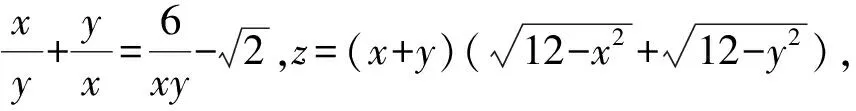
这道题简洁、对称、优美，设有陷阱并有一定的难度，主要考类化归思想、换元思想及数形结合思想，也考查了基本不等式的应用.

2 解法探究

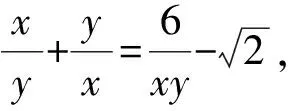
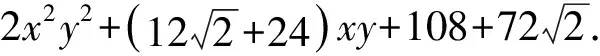
点评：解法中使用两边平方法去掉根号后，关键是观察到已知式与目标式的联系，用xy这个整体作为自变量，通过换元达到化二元为一元的目的，进而求出目标函数的值域.

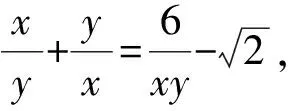
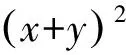
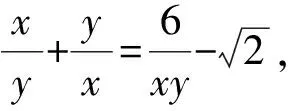
点评：通过对条件式的变形，化成平方和的形式，联想到三角换元方法，从而达到化二元为一元的目的.

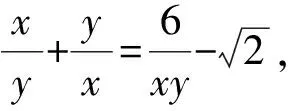
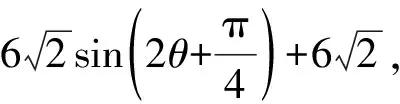
点评：观察到条件式可配凑为余弦定理形式，从而尝试构造三角形将问题求解.

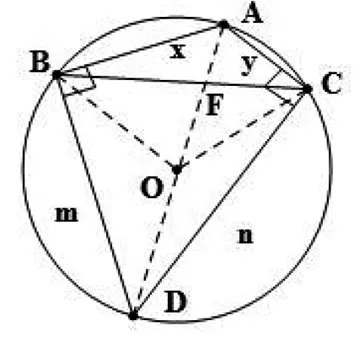
图1

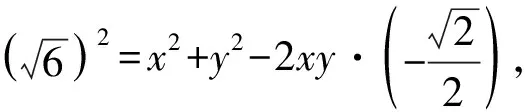
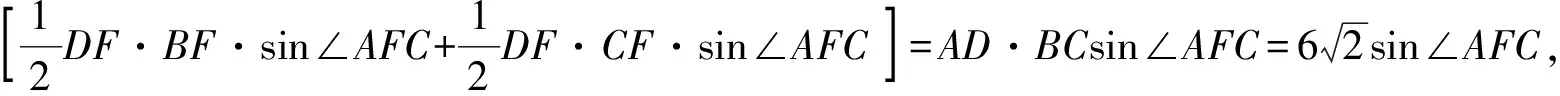
点评：本解法根据题意构造了一个圆内接四边形，从而将所求表示成四边形面积的表达式，再将其转化为一个角的正弦值的函数达到求解目的.

4 解后反思

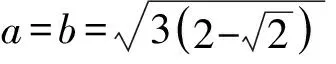
一般地，此类题的解决途径就是想办法将二元函数转化为一元函数，首先看能否用一个变量直接表示另一个变量.然后再看函数能否转化成某个整体的表达式.如果可以，则可采用整体换元的思想.本文中的解法就是将xy、x+y换元成t，或者采用三角换元将双变量转化成单变量θ、∠AFC的函数，实现二元函数的减元目的.实际上，这种题型在近年的考试中多次出现，例如：

题1 (2020江苏高考)已知5x2y2+y4=1(x,y∈R),则x2+y2的最小值为.

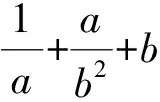
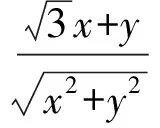
5 追本溯源

本题是一道对思维有较高要求的好题，也是一道源于教材、高于教材命制的试题.其来源于人教2019版数学选修1第58页综合运用第5题，若a>0,b>0,且ab=a+b+3,求ab的取值范围.因此教师在教学中，应重视对课本例习题的深度挖掘，挖掘其中蕴含的数学背景，剖析背后的数学本质，感悟试题设计所蕴含的数学思想等.