基于拓扑优化和Kriging模型的前中盾结构轻量化设计

贾连辉 李晓科 袁文征 何文斌 廖兆锦

1.郑州轻工业大学河南省机械装备智能制造重点实验室，郑州，450002

2.中铁工程装备集团有限公司，郑州，450016

0 引言

盾构机作为大型工程机械装备，广泛应用于地铁、铁路等隧道工程，在国民经济中发挥着重要作用。前中盾作为盾构机的核心部件，其结构设计与作业环境密切相关，通过结构分析及优化提升性能、降低生产制造成本是盾构装备制造企业关注的热点。泥水平衡盾构机具有开挖面稳定、对周边土体扰动小以及地面沉降量控制精度高等优点，在越江隧道和海底隧道中得到广泛应用[1]。泥水平衡盾构机在掘进时沿隧道轴线推进以挖掘土壤，依靠前中盾在未衬砌的开挖隧道段中起临时支撑作用，承受周围土层的压力[2]，因此，在施工过程中，前中盾对隧道的开挖和衬砌起到至关重要的作用。

为保证泥水平衡盾构机在服役过程中的安全性，国内外学者针对整机及零部件展开了结构分析及优化工作。邓立营等[3]给出了土压平衡盾构机刀盘驱动扭矩及盾体总推力的计算方法，为刀盘及盾体的结构设计优化提供了理论依据。徐燕[4]、蒋国亮[5]对盾构整机进行结构设计优化，提出了更安全紧凑的盾构结构。孙剑萍等[6]、秦大同等[7]对盾构刀盘进行受力分析与优化，提高了掘进效率、延长了刀盘寿命。霍军周等[8]以大连刀盘为研究对象，分析了不同工况下刀盘的应力、变形以及模态和谐响应，然后基于ANSYS Workbench平台进行多目标优化求解。王林涛等[9]以盾构推进液压系统为研究对象，基于Kriging近似模型和模拟退火算法进行压力扰动幅值的优化求解，结果表明优化后的目标值得到明显改善。

盾构机的结构分析及优化设计取得了一定进展，但目前研究多集中于刀盘，对前中盾研究较少。前中盾作为盾构机的关键部件，在服役过程中承受着巨大压力，而现有前中盾的结构设计多依赖于已有经验，设计结果过于保守，导致整体质量偏大，造成了资源浪费，因此，有必要根据前中盾的实际服役工况对其进行轻量化设计。

常用的轻量化设计方法包括拓扑优化和尺寸优化。其中，拓扑优化根据给定的负载情况、约束条件和性能指标，在给定区域内对材料分布进行优化，在机械、汽车、航天等领域得到了广泛应用[10]。张璐凡等[11]在连接臂三维建模和有限元分析的基础上，以连接臂的质量最小、寿命最高为优化目标进行了拓扑优化设计。石磊等[12]以飞机起落架扭力臂为研究对象，采用拓扑优化方法获得新的材料分布，并采用遗传算法进行优化求解得到最优的结构尺寸。姜淑凤等[13]以机床横梁轻量化为目标，在静力学和模态分析的基础上，采用相对密度法对机床横梁进行了拓扑优化设计。崔华钊等[14]在重型商务车车架典型工况强度分析的基础上，基于SIMP方法进行了车架的拓扑优化设计，实现了车架总成减重10.5%。

拓扑优化及尺寸优化方法已经在复杂产品的设计优化中得到了广泛应用，近似模型[15-16]的引入进一步降低了优化成本。但由于前中盾服役工况复杂，组成零件众多，目前对其研究较少。因此，针对某型号泥水平衡盾构机，本文对其前中盾进行拓扑优化和尺寸优化设计。

1 前中盾有限元分析

前中盾位于盾构机壳体的前端，其压力隔板装有刀盘驱动，实现隧道开挖。压力隔板将泥土仓与工作部分隔开，通过调节盾构千斤顶作用到压力隔板上的推力来调节泥土仓内的压力，使其与开挖土层的压力达到平衡状态，从而达到支撑和稳定开挖面的作用。作为盾构机服役过程中的关键结构部件[17]，前中盾在掘进过程中承受周围土体及泥水压力、切削阻力、盾构推力的反作用力和铰接油缸的拉力等复杂工况。本节针对某型号土压平衡盾构机，对其进行三维模型构建、约束和载荷施加，在此基础上进行有限元分析。

1.1 前中盾模型的建立

前中盾结构复杂、零部件众多、尺寸较大，直接进行整体焊接装配难度较大，因此，在实际生产中将整个前中盾划分为10个部件块，分别对每个部件块进行焊接装配，最后再将10个部件块组装到一起。本文利用SolidWorks软件分别对10个部件块进行建模并装配形成前中盾三维模型。为降低有限元分析的计算成本，对构建的前中盾模型进行简化处理，忽略结构上对静力学分析结果影响较小的特征，如开孔、开口槽等[18]。前中盾结构三维模型如图1所示。

图1 前中盾三维模型

1.2 前中盾有限元分析

前中盾在实际服役过程中作业环境恶劣、受力情况复杂[19]，一般采用高强度结构钢Q345，其材料力学性能参数[20]见表1。

表1 前中盾材料参数

将前中盾三维模型导入ANSYS Workbench软件中进行网格划分，网格划分采用Solid186单元，六面体结构类型，单元尺寸设置100 mm，单元数量为183 510、节点数量为402 069，前中盾网格模型如图2所示。

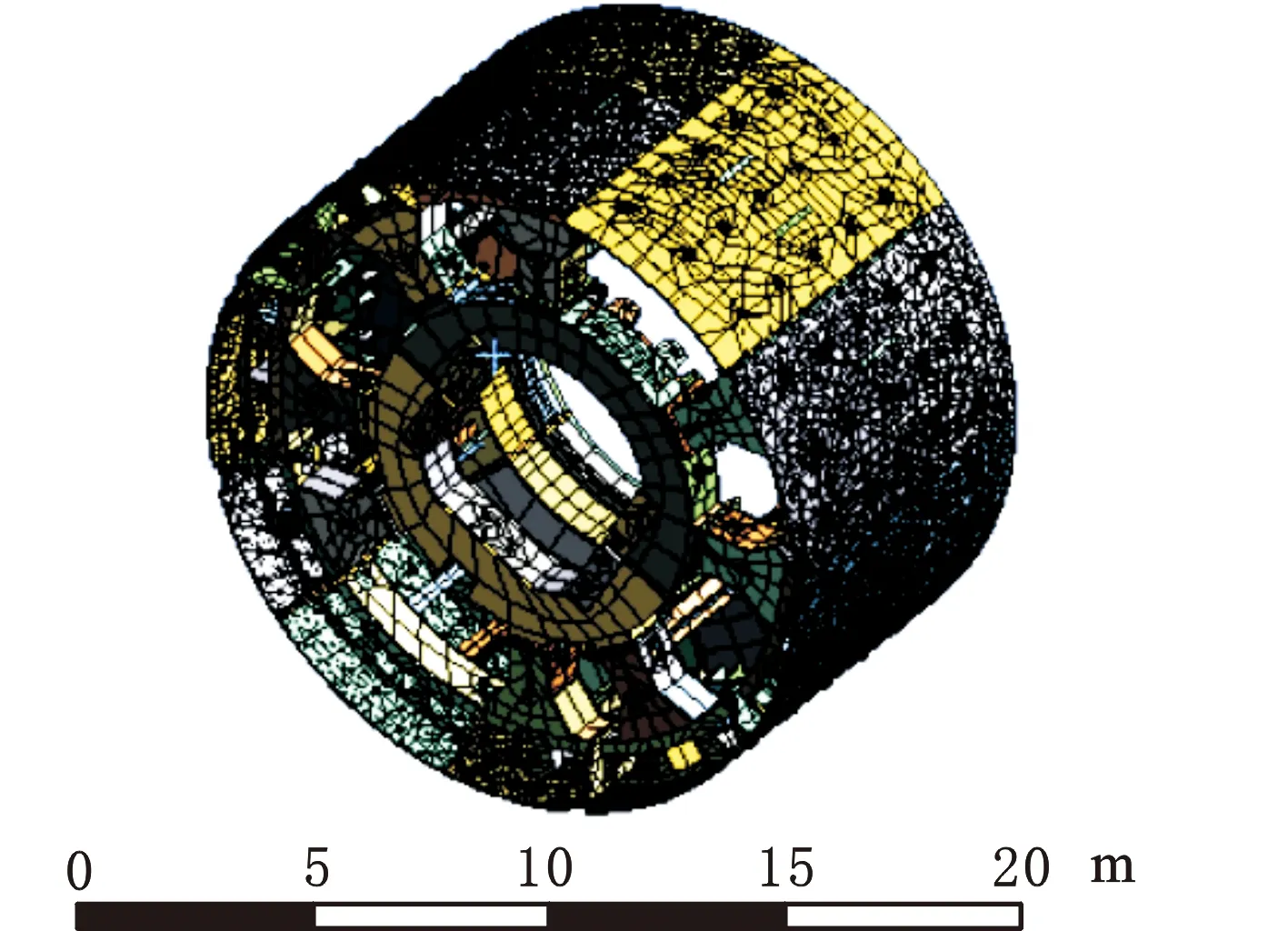
图2 前中盾网格模型

根据盾构机在服役过程所处的工况，将中盾与尾盾连接部位进行完全约束，重力加速度设为9.8 m/s2。由于前中盾的尺寸较大，壳体各部分在地下埋深不一致，因此前中盾壳体外侧所受压力大小是不同的。根据实际测量结果可得，壳体各部分所受压力如表2所示，施加载荷情况如图3a所示。

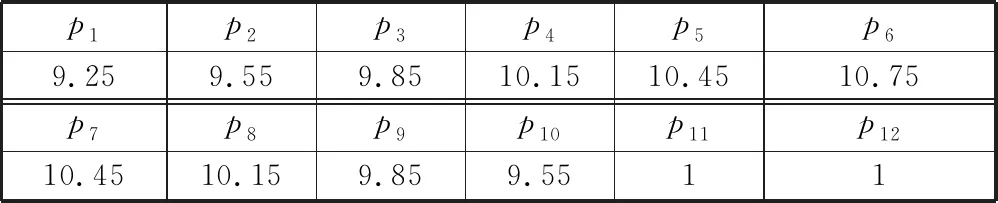
表2 前中盾表面所受压力参数

盾构机掘进时，其正前方前隔板直接与泥水接触，受到水土压力p11作用，其大小为1 MPa。同时，泥水也会被带入前盾内部从而给气垫舱各表面施加压力，因此p12为泥水在盾体内部对外施加的压力，大小为1 MPa。固定约束添加在中盾壳体一周，如图3a～图3c所示。

推进油缸施加给前盾后隔板的推力F2为2.222×108N，后配套拖拉力施加给米字梁的力F3为2.25×106N，安装机施加给米子梁上的弯矩M1为8.8×106N·m，均添加在前中盾背面，如图3d所示。

中心环承受刀盘、主驱动等重力F4为9.5×106N，主驱动防扭油缸施加给前盾导向槽的力F5与F6分别为4.58×106N与4.58×106N，刀盘作用在中心环上的弯矩M2为9×106N·m，均添加在米字梁处，施加载荷如图3e和图3f所示。

(a)外侧壳体受力图 (b)前隔板受力图

以上载荷数据均由中铁工程装备公司提供，符合实际工况且数据准确。对前中盾施加载荷的情况见表3。

表3 前中盾所受载荷

结合上述边界约束条件，根据前中盾的材料特性，对前中盾初始模型进行有限元分析，得到应力分布云图和变形云图结果，如图4a、图4b所示。可以看出，前中盾的最大应力为253.62 MPa，最大变形为4.7845 mm，最大应力集中在中盾隔板上，盾体其余部位受力较小，强度满足设计需求。但该型号前中盾整体质量较大，具备一定的优化空间。

(a)应力云图

2 基于ANSYS的前中盾结构拓扑优化

拓扑优化是在满足在给定载荷和约束条件下，在给定优化区域内寻求结构材料最优分布的一种优化方法[21-24]。根据前中盾的结构布局与装配需求，确定前中盾的优化设计域为内部不涉及装配的筋板。前中盾优化设计域划分结果如图5所示，其中，绿色区域为设计域，其余部分为非设计域。

根据前中盾的实际服役工况和Q345材料特性对其进行拓扑优化设计，保证优化结果满足设计的同时能够达到减小质量和制造成本的目的。盾构机前中盾的拓扑优化整体流程如图6所示。

图6 前中盾结构拓扑优化流程

2.1 前中盾拓扑优化过程及结果

根据轻量化设计要求与初始前中盾的有限元分析结果，本文将拓扑优化目标设置为38%。以前中盾总体质量最小为目标、应力和变形小于许用值为约束，构建前中盾拓扑优化数学模型如下：

(1)

式中，ρ为设计变量；ρmin为最小密度；ρi为相对密度；Vi为相对体积；m为目标函数，即前中盾的总体质量；S、G为前中盾受到的应力和变形；C为前中盾的拓扑优化设计域。

前中盾的拓扑优化采用变密度法通过ANSYS Workbench软件中的Topology Optimization模块完成。

拓扑优化结果如图7所示。可以看出，经过多次迭代后，相较于拓扑优化前，拓扑优化后的前中盾结构中增加了一些空洞。图7中的橙色部分表示可在二次设计中去除的部分。

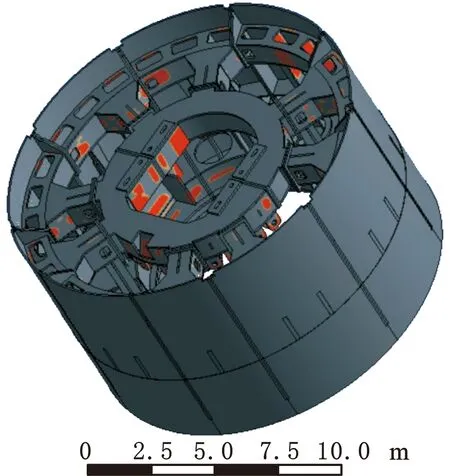
(a)可去除结构部分示意图

2.2 二次设计

优化前的结构如图8a所示。根据图7的拓扑优化结果，并考虑前中盾零部件的加工工艺性，合理去除图中橙色区域，获得拓扑优化后的前中盾结构，如图8b所示。对比发现，拓扑优化后的前中盾结构在非装配区域挖了一些矩形孔，从而实现了减重。

(a)拓扑优化前的结构

3 正交试验和方差分析

3.1 正交试验设计

根据企业经验，选择前中盾壳体厚度x1、前盾前隔板厚度x2、前后封板厚度x3、前盾后隔板厚度x4、推进环板厚度x5、中盾隔板厚度x6、拼装机连接板厚度x7共7个前中盾关键尺寸为优化变量，其结构分布如图9所示。

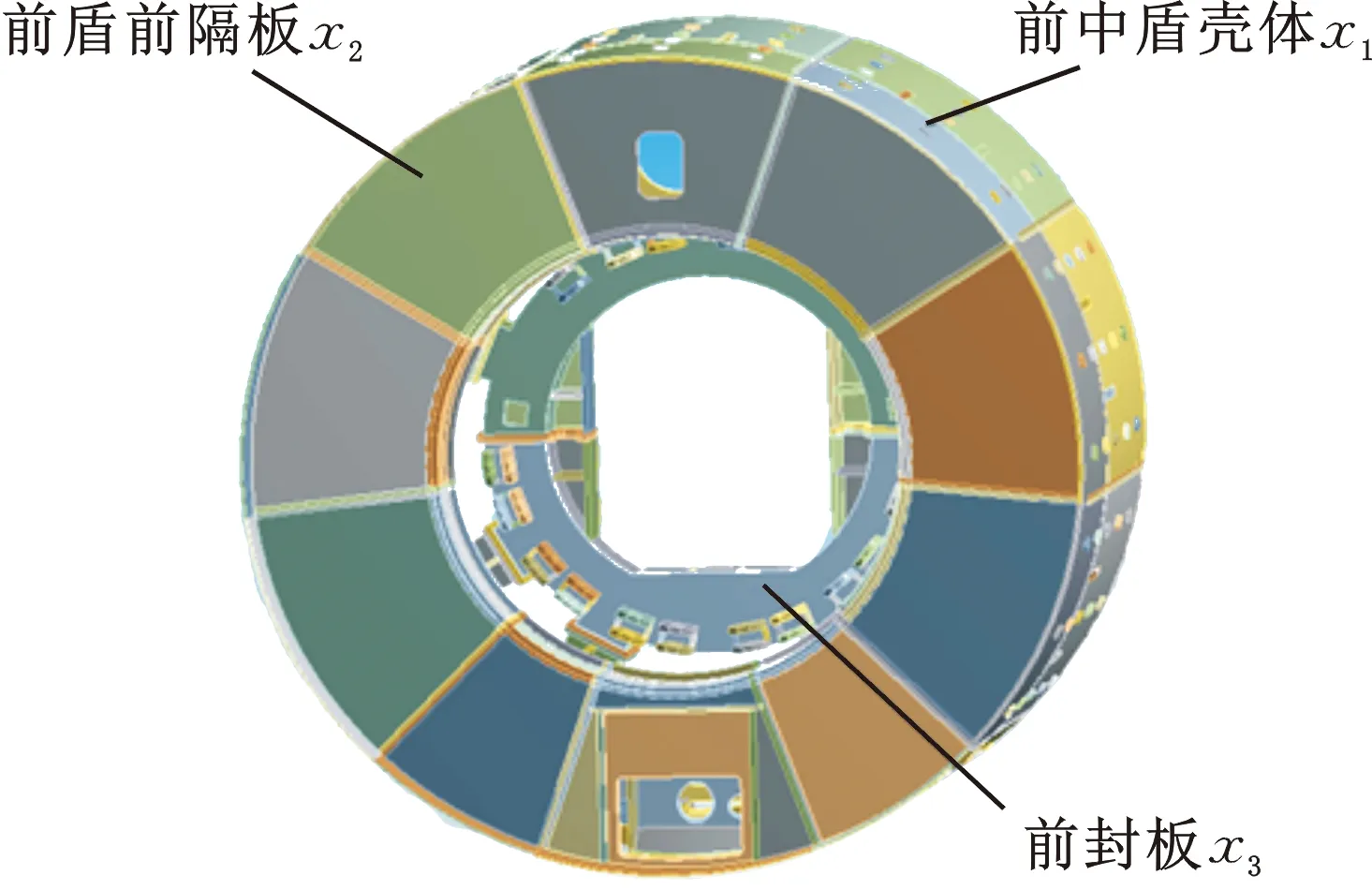
(a)前中盾正面

本文采用7因素3水平的正交试验设计[25]选取样本点，以质量、最大变形和最大应力为性能响应。根据正交试验尺寸对前中盾的三维结构进行重建，并利用ANSYS Workbench软件进行有限元分析，所得结果如表4所示。

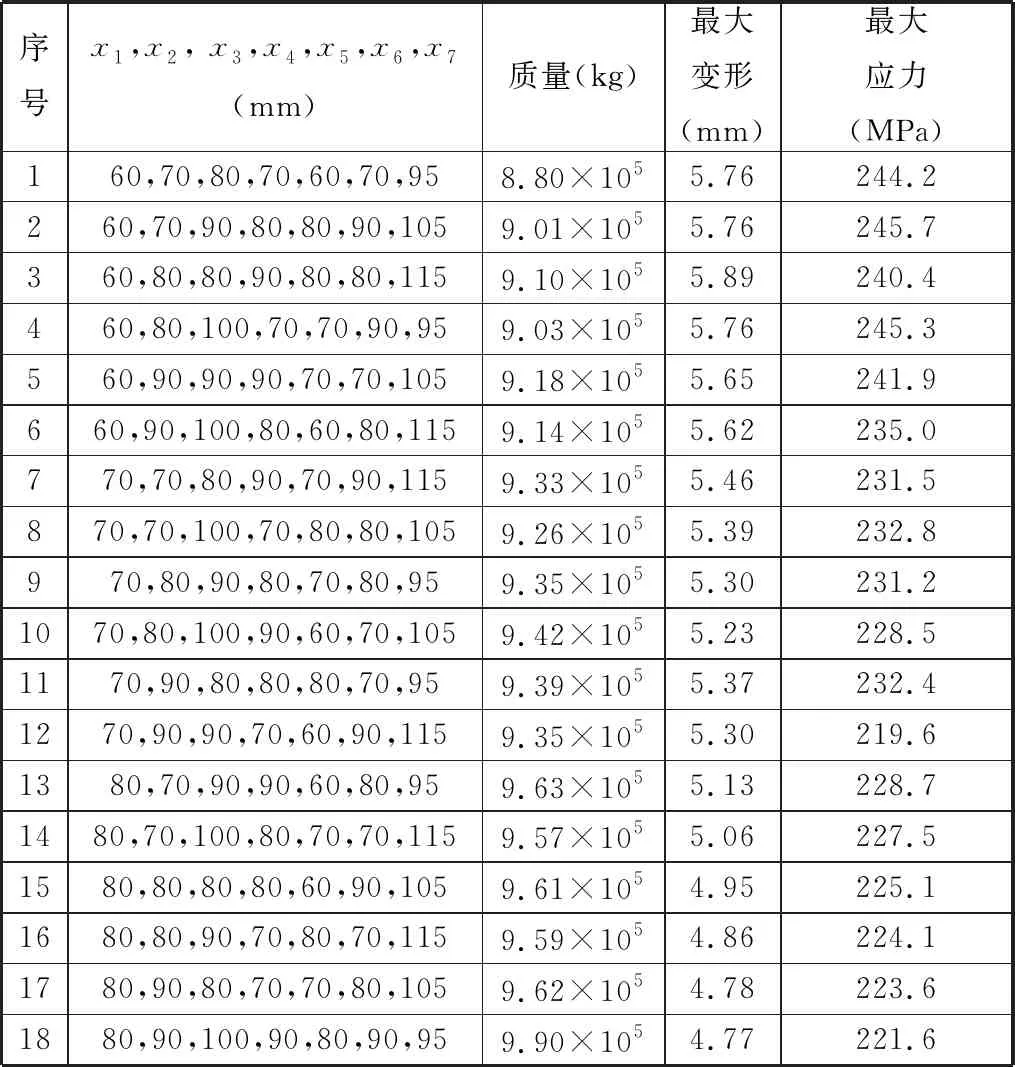
表4 正交试验结果

3.2 多因素方差分析筛选设计变量

多因素方差分析常用来研究3个及3个以上的变量对响应是否产生显著影响。利用表4所得数据，将x1，x2，…，x7与质量、最大变形、最大应力进行多因素方差分析，所得分析结果分别列入表5、表6、表7，其中p<0.05表示影响显著，p<0.01表示影响高度显著。

表5 质量多因素分析结果

表6 最大变形多因素分析结果

表7 最大应力多因素分析结果

针对x1，x2，…，x7这7个因素利用正交试验设计与多因素方差分析进行7因素3水平结果的对比，结果显示，前中盾壳体厚度x1、前盾前隔板厚度x2对质量产生显著贡献差异，前盾前隔板厚度x2对最大变形产生显著贡献差异，前中盾壳体厚度x1、前后封板厚度x3对最大应力产生显著贡献差异，因此将前中盾壳体厚度x1、前盾前隔板厚度x2、前后封板厚度x3作为优化对象，进行前中盾的尺寸优化。

4 前中盾尺寸优化模型

前中盾尺寸优化需要对不同尺寸参数下的质量、最大变形、最大应力进行调用，该过程涉及三维建模、网格划分、有限元分析等步骤，直接调用求解优化成本过高。为此，可引入代理模型近似结构尺寸参数与性能响应之间的隐式关系，进而在优化求解中直接调用近似模型来获得最优的结构尺寸参数。常用的近似模型有多项式响应面[26](polynomial response surface，PRS)、Kriging近似模型[27]、径向基函数[28](radial basis function，RBF)和支持向量回归[29](support vector regression，SVR)等。相较于其他常用的近似模型，Kriging模型逼近鲁棒性好，并且能够给出预测点的误差估计，因此得到了广泛应用。

Kriging代理模型[30-32]的试验点响应取决于设计参数和样本分布，其响应函数组成为

g(x)=fT(x)η+Z(x)

(2)

式中，f(x)为回归函数向量多项式，表示原始黑箱函数的近似趋势；η为系数项；Z(x)表示均值为0的随机过程。

Z(x)和Z(ω)之间的变异函数为

(3)

在可靠性设计优化中，通常采用平方指数函数(即各向异性高斯函数)作为相关性函数，其表达形式如下：

(4)

式中，xi和ωi为点x和ω的第i个分量；n为点x和ω的维度；θi为第个i方向相关长度系数的标量值。

最优拉丁超立方试验设计方法属于分层采样，是一种用采样值反映随机变量的整体分布的方法，能有效减少复杂仿真系统试验的次数，缓解仿真试验计算量增长的压力[33-34]。通过最优拉丁超立方试验设计方法抽取45组样本点，样本数据如表8所示。

表8 部分样本点

以前中盾壳体厚度x1、前盾前隔板厚度x2、前后封板厚度x3为尺寸变量，以前中盾最大变形G和最大应力S为约束条件，前中盾的许用位移计算公式为[34]

f=0.1%D

(5)

式中，D为前中盾的直径，14.7 m。

计算得到前中盾最大变形G的取值范围为[0，14.7] mm。通过查阅GB/T 1591—2018标准可知，Q345的屈服强度为345 MPa，即前中盾可承受最大应力为345 MPa。在服役时，取安全系数为1.5[35]，计算得到最大应力S的范围为[0，230] MPa。以前中盾质量最小为优化目标，综合考虑最大变形、最大应力等性能指标，以前中盾结构尺寸x1、x2、x3为设计变量，建立前中盾轻量化模型表达式如下：

(6)

式中，X为设计变量；f(X)为前中盾质量；G(X)为最大变形；S(X)为最大应力。

5 模型求解及验证

5.1 尺寸优化

采用序列二次规划算法[36]对前中盾尺寸优化模型进行求解，其表达式如下：

(7)

式中，Xk为迭代设计点；∇Gi(Xk)、∇Si(Xk)分别为G(X)、S(X)在Xk处的一阶导数值。

整体建模及优化过程通过MATLAB软件实现，x1、x2、x3优化结果分别为60 mm、74.8020 mm和95.1980 mm，根据企业生产实际，对优化结果进行取整处理，得到最优的设计参数结果为60 mm、75 mm和95 mm。

5.2 结果验证

根据优化结果进行三维建模、网格划分、载荷施加及有限元分析，得到优化后的前中盾应力与变形如图10所示。

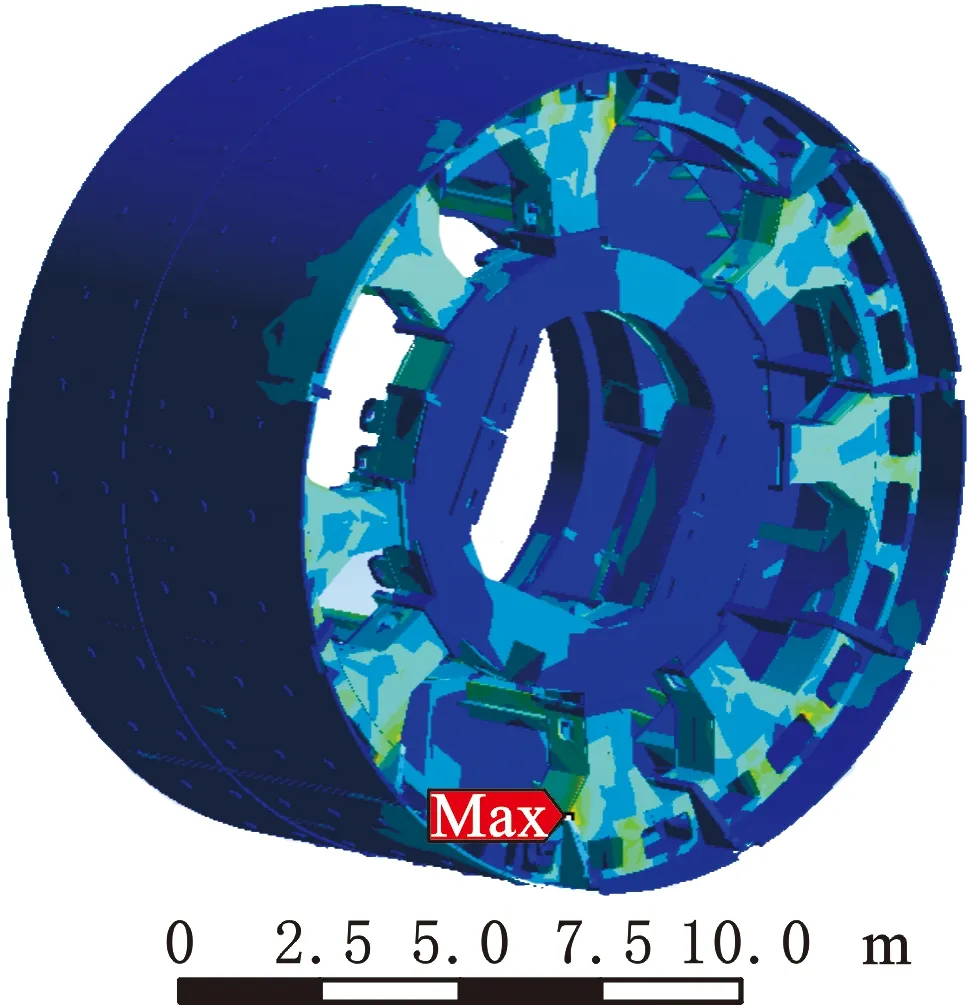
(a)应力云图

初始前中盾结构和二次轻量化后的前中盾结构性能比较如表9所示。可以看出，经过两次轻量化后的前中盾质量为932 t，相对原始质量减重30 t，减重比例达3.1%。此外，优化后的前中盾结构最大应力相较于初始值有大幅减小，表明中盾隔板处的应力集中经过优化后有明显改善，最大变形同步减小，表明优化后的前中盾整体刚度得到提高。

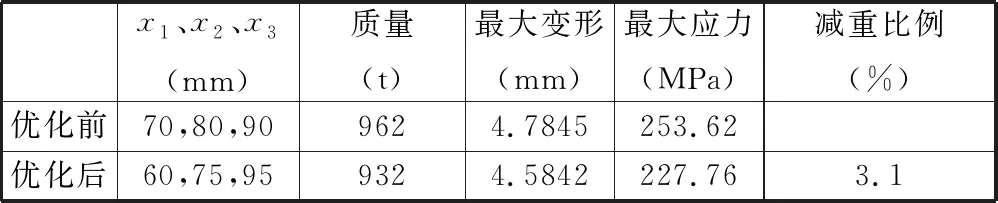
表9 前中盾尺寸优化结果

6 结语

本文以某型号土压平衡盾构机为研究对象，对其前中盾结构进行轻量化设计，具体工作如下：

(1)建立了现有前中盾结构的三维模型，并通过ANSYS Workbench软件进行静力学分析和拓扑优化，并根据拓扑优化结果进行二次结构设计(一次轻量化设计)；

(2)针对二次设计的前中盾结构，利用正交试验和方差分析，筛选出对性能影响较大的3个结构尺寸参数作为二次轻量化的设计变量，在此基础上构建前中盾结构尺寸优化模型；

(3)为减小优化过程中直接调用变量-响应数据的计算成本，采用最优拉丁超立方试验设计和有限元分析，获取45组变量-响应参数组合，并通过Kriging模型拟合前中盾结构尺寸参数与最大应力、最大变形之间的隐式关系；

(4)通过序列二次规划算法调用变量-响应隐式关系近似的Kriging模型，获得最优结构参数组合，为符合生产实际，对优化结果进行圆整(二次轻量化)；

(5)利用有限元分析对二次轻量化得到的前中盾结构进行验证，结果表明，相对于原始前中盾结构，采用本文提出的轻量化设计方法得到的前中盾结构在满足服役需求的同时，能够有效减小整体质量。