面向催化剂载体应用的TiO2多孔陶瓷结构优化设计

邹无有 杜 纯 艾建平 单 斌

1.华中科技大学材料科学与工程学院，武汉，430074

2.江西科技师范大学材料与机电学院，南昌，330038

0 引言

多孔陶瓷又称气孔功能陶瓷，是具有一定尺寸和数量孔隙结构的新型材料，它既具有传统陶瓷材料耐高温、耐腐蚀等优点，又具有高孔隙率、高比表面积、高比强度和良好渗透性的特点[1-2]，目前已被广泛应用于航空航天[3]、生物医疗[4]、环境催化[5-7]、能源[8-9]等领域。尤其在环境催化中，多孔陶瓷的催化剂载体可有效解决传统粉末催化剂分离难、可回收性差，以及块状催化剂催化效率低的问题，提高了活性金属原子利用率，实现了贵金属减量化利用，节约了工业生产成本。此外，多孔陶瓷载体负载活性组元可有效避免纳米活性颗粒聚集失活，维持活性组元的高催化活性和稳定性，成为当下催化领域的重要组成部分[10]。当前，内燃机排放控制、石油和天然气工业下游气体处理、污水处理等环境催化领域常用的催化剂载体均为蜂窝陶瓷，其通道内流动为层流，缺乏径向的传质和传热，限制了催化反应的扩散，需要通过扩大整体尺寸来弥补，难以满足当下日益严格的环境保护法规[11-13]。

压降、比表面积及机械性能是催化剂载体的关键评价指标。低压降可令流体流过催化剂载体的阻力减小，进而降低能量消耗，并提供高空速，实现短接触时间内的连续反应；高比表面积可负载更多活性组分，并增强其分散度，提高催化剂活性；高机械性能有助于催化剂载体经受流体流动产生的振动和冲击，维持较好的稳定性。这三个关键性能主要取决于材料的自身物理性能及载体内部的结构特征[14]。关于材料，研究表明过渡金属氧化物催化剂载体由于自身的晶格缺陷、电子结构和化学性质，可进一步提高催化剂的活性，其中TiO2陶瓷具有光催化活性高、化学性质稳定、生物相容性好、原料来源丰富以及成本低廉等优点，被广泛应用于防晒护肤品、太阳能电池、水污染处理等生物医学、能源、环保、催化领域，具有巨大的功能化催化剂载体及光催化材料应用潜力[15-16]。关于结构，为克服传统蜂窝陶瓷存在的问题，研究人员提出了周期性点阵结构[17]。周期性点阵结构具有高孔道连通性，以及优异的径向传质和传热能力，可通过更少的催化表面来实现与蜂窝陶瓷相同的污染物转化率，有效减少了催化剂用量，但也产生了更高的压降[18]，进而降低了反应空速和催化效率。对此，AL-KETAN等[19]提出了基于最小表面框架的具有可控制拓扑结构的三周期极小曲面(TPMS)催化剂载体，并且通过模拟及实验研究了三种不同TPMS结构对于催化剂载体的机械性能和压降的影响。SHUAI等[20]通过模拟对比不同晶格数、孔隙率的氧化铝陶瓷的机械性能，发现更复杂、更合理的网格结构表现出更佳的抗压强度。WU等[21]通过实验和数值研究探讨了不同孔径、孔隙率、温度和速度对陶瓷泡沫的压降、流场特性及传热的影响。CORNEJO等[22]提出了一个基于物理的详细模型，使用大量计算实验研究了正方形、六边形和三角形截面形状的单通道模型对蜂窝型基材的压降的影响。然而，以上研究均集中于探讨不同现有结构之间的差别、孔隙率和环境因素对性能的影响，缺乏结构自身构成要素对性能的影响机制的探究，针对催化应用的多孔结构的设计也少有报道。

传统成形方法难以克服多孔陶瓷韧性差和内部孔道结构复杂的问题，无法达到多孔结构优化设计的要求[23]，而增材制造技术基于离散-堆积原理，具有成形效率高、成形精度高的特点，可满足任意复杂几何结构的成形，为构建具有可控宏观周期性点阵结构的多孔陶瓷提供了强大的工具[24-26]。

本文构建了一套适用于周期性点阵结构多孔陶瓷的压降和机械性能的仿真模型，通过数字光处理(digital light processing，DLP)的光固化增材制造技术实现了具有精细微结构的TiO2多孔陶瓷的快速制造，并结合4种不同多孔结构的实验测试结果对仿真模型进行了验证和修正。同时，利用模拟探究了结构构成要素对压降和机械性能的影响规律，基于此对周期性点阵结构进行了设计优化，最终获得了一种兼具低压降、高机械性能、高表面积的新型周期性点阵结构，进一步扩展了多孔陶瓷在催化剂载体领域的应用。

1 材料和方法

1.1 周期性点阵结构描述

周期性点阵结构由点阵单元通过周期性排布堆叠后得到，其构成可分为三个层次，如图1所示。第一层次为支柱，通过支柱形状和角度、杆长度、杆直径和杆数量等因素组合得到第二层次点阵单元，点阵单元再通过阵列数、阵列角度及阵列方向等因素得到第三层次周期性点阵结构。上述因素决定了周期性点阵结构的表面积及孔隙率，进而影响催化剂载体的可负载面积、压降及机械性能。

(a)支柱 (b)点阵单元 (c)周期性点阵结构

本文周期性点阵结构的设计分为4个阶段：仿真模型验证结构的设计与光固化增材制造，压缩及压降实验与模拟的对比及仿真模型的修正，角度a、b、c对性能的影响机制的模拟探究，具有优异催化剂载体应用性能的多孔结构的优化设计，具体技术路线如图2所示。

图2 结构设计技术路线

1.2 点阵结构优化设计方法

点阵结构优化设计的方法较多，包括基于图像设计、拓扑优化、基于CAD等。其中，基于图像设计是指利用计算机断层扫描(CT)或其他扫描工具获得的结构数据来重建结构内部的缺陷，构建真实的多孔结构，并基于该结构进行分析设计。拓扑优化是根据给定的负载情况、约束条件和性能指标，在给定的区域内对材料分布进行优化，其优化对象为产品的拓扑结构。基于CAD是指利用计算机及其图形设备对不同方案进行大量计算、分析和比较，以帮助优化设计确定最佳结构。相较于其他方法，CAD能够大幅减轻设计人员的劳动，缩短设计周期并提高设计质量，考虑到周期性点阵结构的构成参数多样、结构复杂，需要多次对比不同参数的结构方案，本文采用CAD方法来进行优化设计，同时结合单因素优化分析方法来探究点阵结构的结构参数对性能的影响机制。

1.3 增材制造

本文主要采用DLP技术对周期性点阵结构进行打印成形，成形流程可分为浆料配制、打印成形、热处理三个部分，具体流程如图3所示。

图3 数字光处理流程图

用于配制陶瓷树脂混合浆料的材料如下：①TiO2和MgO粉末(粒径为1 μm，石家庄浩诚新材料科技有限公司)；②双聚丙烯二醇二丙烯酸酯(DPGDA)、脂肪族聚氨酯丙烯酸酯(8402)、脂肪族二丙烯酸酯(130)(展鑫树脂上海有限公司)；③光引发剂(2，4，6-三甲基苯甲酰基)二苯基氧化膦(TPO)、苯基双(2，4，6-三甲基苯甲酰基)氧化膦(819)、2-羟基-2-甲基苯基丙酮(1173)(展鑫树脂上海有限公司)；④有机硅表面活性剂SH300(湖北隆盛四海新材料股份有限公司)；⑤蔗糖(国药控股有限公司)。配制方法如下：①在避光条件下，将130、8402和DPGDA按5∶2∶3的比例混合在一起，依次加入光引发剂TPO、819、1173(质量分数均为混合树脂的8%)、SH300(质量分数为混合树脂的9%)，搅拌均匀，得到半透明液体；②往上步骤的液体中加入TiO2(体积分数为25%)、MgO(质量分数为TiO2的5%)，适当搅拌后，以350 r/min的转速用氧化锆球磨珠球磨6 h，得到所需浆料。

将陶瓷浆料倒入3D打印机(醴陵九天科技有限公司)中，采用自上而下的方式打印。打印时通过平台正上方放置的投影仪提供的紫外线光源来固化成形平台上的浆料，每投影固化一层，成形平台下移一定距离，通过刮刀刮平表面后进行下一层成形。打印模型通过SolidWorks软件进行设计绘制，然后利用3D打印设备自带的软件进行切片处理，打印参数为层厚25 μm，曝光时间20 s(前三层30 s)。成形后用乙醇和水冲洗掉样件上多余的浆料，经紫外灯光照固化4 h后获得TiO2周期性点阵结构素坯。

将素坯放入微波烧结炉(长沙普金能源科技有限公司)中进行一步法脱脂烧结。素坯在空气氛围中，先以27.5 ℃/min的升温速率从室温加热到550 ℃，然后保温20 min，再以10 ℃/min的升温速率加热到1350 ℃，并保温40 min，最后随炉自然冷却至室温。

1.4 测试与表征

采用具备超高放大率镜头变焦的VHX-1000C超景深三维显微镜和Nova NanoSEM 450型扫描电子显微镜观察打印样件表面；采用自搭的测试平台测量打印样件压降，该测试平台包括一个高精度差压表、一个量程为5～45 L/min的转子流量计、一台气泵及部分气路管道和接口，测试模型为φ10 mm的圆柱形，壁厚为1 mm，高为9 mm，测试速度为5～45 L/min，如图4a所示；采用材料高温持久性能试验机AG-IC 100 kN测定打印样件的单轴压缩机械性能，压缩样件模型尺寸为6 mm×6 mm×6 mm，测试速度为0.3 mm/min，如图4b所示。

1.5 数值模拟

周期性点阵结构的优化设计过程涉及较多模型，采用有限元分析方法进行辅助分析以简化过程，可实现结构设计的快速优化和验证。本文主要在ANSYS中进行数值模拟，涉及流体仿真和结构仿真两个部分。在流体仿真过程中，针对模型的流体域施加速度入口和质量守恒出口边界条件[27]，如图4c所示，所有结构均划分为约600万个四面体单元，单元质量平均值约为0.9，满足模拟要求。在结构仿真过程中，对模型本身施加力载荷和固定约束，如图4d所示[28-30]。所有结构均划分为约170万个四面体单元，单元质量平均值约为0.85，满足模拟要求。

(a)压降测试 (b)单轴压缩测试

2 结果与讨论

2.1 仿真模型验证与修正

按照上述构建仿真模型，设计4种不同类型的多孔结构作为研究对象，如图5所示。这4种结构都是目前常见的周期性点阵结构，且4种结构之间的结构参数a、b、c、m存在较大差别，可通过实验数据与仿真结果之间的对比，充分验证不同结构参数的多孔结构仿真模型的准确性，以验证该仿真模型对所有周期性点阵结构都适用的合理性。

首先对压降进行验证，将图5中的4种结构分别填充于直径10 mm、壁厚1 mm、高9 mm的圆筒中，并采用1.3节所述陶瓷浆料配制第一步所获得的半透明液体树脂进行打印，以获得具有更光滑表面的样件，降低实验样件与仿真模型间的差别。打印样件如图6所示。

(a)简单立方 (b)八面体1

(a)简单立方 (b)八面体1

采用1.4节所述测试方式获得了4种不同结构的压降随流速的变化关系，并与仿真结果进行对比，如图7所示。对于同一结构，压降随流速的增大呈指数增长，主要是因为流速的增大引起了流体与多孔固体之间及流体自身的碰撞频繁，速度变化加剧。不同结构的压降差距较大，在35 L/min的流速下，八面体3的实验压降均值为709.7 Pa，比八面体1高472.7 Pa，表明结构对压降的影响较大，因为不同结构的结构构成要素的参数不一样。此外，由图7可以发现，多次实验数据之间的差距较小，表明实验稳定性较好，且4种结构的实验数据与仿真数据之间的误差较小，基本都在5%以内，个别数据在10%左右，均在可接受范围，证明压降仿真模型可信，符合实际。

(a)简单立方 (b)八面体1

接着对压缩机械性能进行验证，压缩样件模型如图5所示，尺寸为9 mm×9 mm×9 mm，压缩实验结果如图8所示。压缩样件在烧结过程中产生了尺寸收缩，如图8e、图8f所示，测试数据表明样件的线收缩率基本稳定在0.3～0.35之间，体积收缩率在0.68左右，符合打印所使用陶瓷树脂混合浆料中的固体组分含量。此外，样件在打印高度方向的线收缩率略高于垂直打印方向，因为样件是叠层固化成形，打印高度方向层间结合度弱于垂直打印方向，而烧结过程中的陶瓷致密化可以提高层间结合，导致样件在打印高度方向的收缩略高。采用超景深对压缩样件表面进行了观察，结果如图8b所示，可以发现样件表面出现明显的阶梯式分布，这与DLP成形工艺相关，该工艺将模型切片为连续变化的薄层，对应非连续变化的固定投影画面，故样件表面为非连续的阶梯。采用扫描电子显微镜对烧结前后样件的表面微观形貌进行观察，结果如图8c、图8d所示，可以发现烧结前样件颗粒粒径较小，相对分散，相互之间通过已固化树脂黏结在一起，而烧结后的样件颗粒粒径较大，在3 μm左右，颗粒之间连接紧密，孔隙较少，表明陶瓷颗粒已经长大且致密化，样件已烧结完全。

(a)烧结前后对比图 (b)样件表面图

采用材料高温持久性能试验机对压缩样件进行压缩实验，并将实验结果与仿真结果进行对比，如图9所示，其中左半部分为仿真结果轴侧视图，右半部分为实验结果图。简单立方结构的仿真结果中应力集中分布在承力杆上(红圈处)，对应在压缩实验中整体呈现“崩溃式”断裂，承力杆全部碎裂，只有部分非承力杆结构得以保留。八面体1、2、3结构的仿真结果中应力分布较简单立方结构更均匀，最大应力集中在基本单元交界处稍上或稍下位置(红圈处)，主要源于交界处面积小，且存在夹角，易引起应力集中[30]，对应在压缩实验中基本呈现45°的断裂带，且断裂点都在交界处附近。采用扫描电子显微镜对压缩件断面进行观察，结果如图10所示，可以发现4种不同多孔结构的断面形貌基本一致，与断裂前存在明显区别，如图10c、图10d右半部分未断裂处和左半部分断裂处的对比，这4种都属于晶粒撕裂的穿晶断裂，这是因为TiO2增材制造过程中加入了烧结助剂MgO，在烧结时MgO会与TiO2产生固相反应，在晶界处形成MgTi2O5，增强了晶界强度。综上所述，4种不同多孔结构的应力分布仿真结果均与实验结果匹配，说明仿真得到的应力分布是可信的。

(a)简单立方

(a)简单立方 (b)八面体1

通过压缩实验和静态力学仿真得到的力和位移曲线见图11。仿真过程中材料参数采用TiO2的标准物理参数，密度为4.26 g/cm3，弹性模量为230 GPa，泊松比为0.27。结果表明，在达到同一断裂应变的情况下，简单立方结构的压缩力最大，八面体3结构的压缩力最小，八面体1的压缩力略大于八面体2结构。对于不同结构的最大压缩力，仿真结果和实验结果具有较好的匹配度，但4种不同结构的实验最大压缩力分别为575 N、378 N、347 N、191 N，仿真最大压缩力分别为6104 N、3239.8 N、2121.3 N、1928.1 N，两者之间相差了1个数量级，这源于实验样件在样件表面及内部会产生一定的缺陷，其材料参数远低于仿真使用的标准值。

(a)实验结果图

针对上述验证过程中最大压缩力数值不匹配的情况，本文对仿真模型中的结构仿真部分进行修正。通过3D打印使用相同打印条件获得部分弯曲样件，采用弯曲测试获得样件弯曲性能参数，利用弯曲法弹性模量测定计算公式获得3D打印样件的弹性模量，为4 GPa，修正材料参数后再次进行了压缩模拟，结果如图12所示。同种结构的不同样件之间存在差别，但总体上在同一个数值附近波动，这源于不同测试样件产生的缺陷数量及位置不同。修正后的仿真结果与实验结果较为匹配，误差在10%以内，主要源于实验样件存在阶梯式表面及缺陷。其中，八面体3结构的差距相对较大，因为它成形时的投影光区域更密集，实际成形实体更加大于模型，且夹角处更圆滑，故实际样件的实验结果与仿真结果差距更大。总体而言，对仿真模型进行修正后，最大压缩力的仿真值与实验值在一定误差范围内相匹配。

(a)简单立方 (b)八面体1

综上所述，通过修正后的仿真模型获得的仿真结果与实验结果在一定误差范围内的匹配度较好。

2.2 结构构成要素对性能的影响

本文以最常用的简单立方结构为研究对象，利用修正后的仿真模型对不同结构参数的模型进行仿真，模型参数如表1所示，保证其他参数一致，即各模型的m1=m2=m3=1，L1=L2=L3=1.5 mm，阵列数为6×6×6，孔隙率为0.79，根据仿真结果进行了压降、应力分布及大小分析，以探究结构构成要素对性能的影响机制。

表1 不同结构模型参数

首先探究角度a对性能的影响，考虑结构的周期连续性，角度a的取值范围为45°～135°，本文选取45°、60°、90°、120°、135°等5个数值进行仿真研究，控制模型的孔隙率一致，模型具体参数如表1中序号1～5所示，仿真结果如图13、图14所示。由图13a、图13b可知，当a=90°时，多孔结构的压降取得最大值541.5 Pa，当a变化时压降出现非对称型减小，当a=135°时取得最小值371.3 Pa。因为角度a的变化让支柱倾斜，流体与模型的碰撞从同时发生变为逐步发生，减小了阻碍力，故压降变小，但a变化时还会在流体流动方向的平面上产生夹角，a较小时夹角开口方向与流体流动方向相反，产生冲击导致压降变大，故压降呈现非对称型变化，且a越大压降越小。由图13c可知，多孔结构的表面积随角度a的变大或变小而变大，当a=90°时取得最小值1111 mm2。由图13d可知，当a=90°时，多孔结构的应力出现最小值93.708 MPa，且应力随a的变化出现对称型增大。因为角度a变化时产生的夹角形成了应力集中，且a越大或越小则夹角越尖锐，应力集中更明显，机械性能也越低，图14a～14e也展现了这一特点，最大应力从a=90°时的大范围分布逐步过渡为a=45°和135°时的夹角处集中分布。

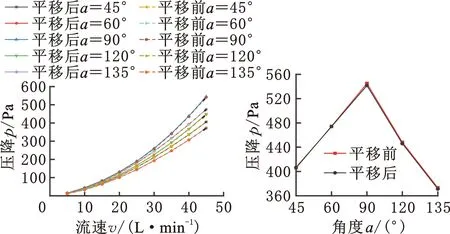
(a)压降 (b)流速为45 L/min时的压降

在其他参数不变的条件下，对垂直流向平面的支柱进行整体平移，将角度a的取值范围扩宽为26.6°～153.4°，对比平移前后的模拟结果，如图13所示。结果表明，平移后压降几乎没有变化，模型的表面积无变化。虽然平移改变了入口和出口的流动情况，但由于多孔结构整体长度相对较长，减弱了该情况带来的压降变化，所以压降无明显差别。由图13d可知，平移后应力略有增大，这是因为平移后夹角更接近承力面，应力集中更加明显，如图14f所示。综合而言，平移对性能的影响较小。

(a)a=45° (b)a=60°

接着探究角度b对性能的影响。角度b的取值范围为0°～90°，本文选取15°、30°、45°、60°、90°等5个点进行仿真研究，控制模型的孔隙率一致，模型具体参数如表1中序号3、6～9所示，仿真结果如图14、图15所示。由图15a、图15b可知，角度b越大，压降越小，当b=90°时取得最小值541.5 Pa。因为b的减小令垂直流向平面出现大量夹角，增加了孔道形状的复杂程度，加剧流体碰撞。由图15c可知，模型的表面积在b=45°处获得最大值1158.6 mm2，因为角度变小会导致杆件变细长，故表面积增大，而当角度小于45°时，杆件之间会产生大量重合，使模型的表面积减小。由图15d可知，应力在b=90°处取得最小值93.708 MPa，应力随着b的减小而增大。因为b=90°时垂直流向的杆件对称分布，对承力杆影响较小，角度变小时，杆件间出现夹角，引起部分应力集中，导致机械性能下降。当b从30°变为15°时，支柱的重合令夹角远离了承力杆，故应力有所减小。图14c、图14g～图14j也展现了这一特点，当b=90°时最大应力大范围分布在主承力杆，角度变小时，最大应力分布区域也变小，集中在夹角附近，而角度进一步减小时最大应力集中区域则少量增加。

(a)压降 (b)流速为45 L/min时的压降

最后，探究了角度c对性能的影响。角度c的取值范围为0°～b，本文以前述结果为基础，选取b=30°、45°、60°、90°时不同的c取值进行仿真对比，模型具体参数如表1中序号10～13所示，仿真结果如图16所示。由图16a～图16d可知，在b一定的情况下，c值越小则压降越小，因为c变大后改变了垂直流向平面内的支柱分布，令孔道形状变复杂，且面积变小，导致流体速度变化加剧。由图16e可知，c越大则表面积越小，但当b=90°时夹角c越大表面积越大。这源于夹角c变大后，垂直流向平面的支柱部分变粗短，部分变细长，表面积增加小于表面积减少，故模型表面积变小；而b=90°时夹角c变大导致垂直流向平面的支柱全部变细长，故表面积大幅增大。由图16f可知，c越大则应力越小，当b=90°时基本不变。这源于夹角c变大后改变了垂直流向平面夹角分布，令大部分夹角数值更接近90°，减弱了夹角的应力集中，在一定程度上改善了多孔结构的受力情况；但当b=90°时，其夹角均为90°，故c变化的影响较小。综上所述，当b一定时，夹角c越小压降和应力性能越优。

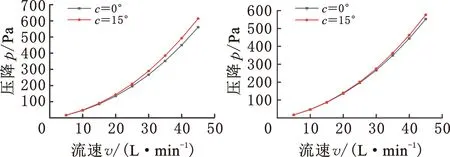
(a)b=30°压降 (b)b=45°压降

基于上述仿真结果，对于三个不同的结构参数a、b、c，采用数据拟合(曲线拟合)法归纳各因素对压降、表面积、应力性能的影响的数学模型，拟合结果如图17所示，拟合方程如下：

p=-0.073(a-87.14)2+1.85b-0.089b2+0.0007b3+5.18c-0.22c2+0.0024c3+578.19

S=0.022(a-90)2+1.34b-0.016b2-1.63c+0.033c2+1128.06

σ=0.0077(a-90)2+0.16b-0.004b2+0.000 024b3-0.27c+0.0073c2-0.000 052c3+97.49

由图17可知，不同性能的结构参数影响曲线的模拟数据与拟合数据基本重合，各性能拟合曲线的R2值分别为0.998、0.977、0.985，调整后的R2值分别为0.994、0.962、0.963，两者之间差距较小，且都接近于1，表明模型拟合度较高，拟合效果较好。

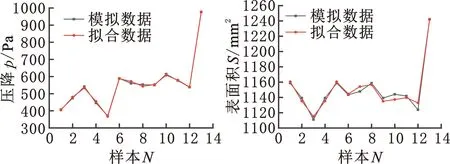
(a)压降 (b)表面积

2.3 高性能结构的优化设计

多孔陶瓷的压降性能与机械性能一般是负相关的，但应用时需要压降性能、机械性能和表面积均较好，本文基于此设计理念，结合上述仿真结果，以a=153.4°、b=90°、c=45°的结构参数设计了一种新型周期性点阵结构，如图18a所示。较大的a值可以获得低压降和高表面积，较大的b值和较小的c值可以获得低压降和高机械性能，如图18c、图18d所示，可以发现设计结构在流速为45 L/min时的压降为231.8 Pa，相较于简单立方结构减小了57.2%，表面积为1391.8 mm2，增大了25.3%，应力为116.53 MPa，增加了24.4%，这来源于夹角造成的应力集中，如图18b所示。为了提高其机械性能，对设计结构进行优化，在夹角处采取平滑处理以减少尖锐角的存在，优化后其压降和表面积基本无变化，应力为105.05 MPa，减小了10%。优化设计后的结构明显改善了多孔结构的性能，在少量降低机械性能的情况下大幅提高了表面积和压降性能，有利于扩展该结构在催化剂载体领域的应用。

(a)设计结构模型 (b)设计结构最大应力区域

3 结论

本文结合增材制造和模拟仿真技术，采用基于计算机辅助设计方法，结合单因素优化分析方法对周期性点阵结构进行了优化设计。

通过光固化成形方式快速制备了具有精细微结构的多孔TiO2陶瓷，发现样件在烧结后产生了0.3～0.35的线收缩，且样件表面呈现阶梯式分布，这是由成形方式和浆料配方所造成的。

对样件进行了压降和压缩实验，根据实验结果对构建的仿真模型进行了验证与修正，研究数据表明，修正后的仿真模型获得的仿真结果与实验结果在一定误差范围内相匹配。基于此，进一步探究了结构构成要素对性能的影响机制，结果表明角度a的增大引起流向水平面内产生大量开口同流向方向的夹角，减缓了流体流动过程中的撞击过程和流速的变化剧烈程度，导致压降减小，但夹角的出现也引起了应力集中，降低了结构的机械性能。角度b的减小和角度c的增大则令垂直流向水平面内的孔道形状及分布更不均匀，使流体压降增大，且夹角产生的应力集中也令机械性能降低。

基于协同优化压降和机械性能的设计理念，采用a=153.4°、b=90°、c=45°的结构参数设计了一种用于催化剂载体的新型周期性点阵结构，并进行了优化。优化设计后的结构与简单立方结构相比压降减小了57.2%，表面积增大了25.3%，表现出良好的应用性能，但其机械性能略有降低，这与结构中存在的夹角有关，有待后续进一步研究。本文为多孔陶瓷在应用过程中的结构设计提供了一种有效的方法。