基于分数阶模型的纱线蠕变性能模拟与预测
李 杨, 彭来湖,2, 郑秋扬, 胡旭东
(1.浙江理工大学 浙江省现代纺织装备技术重点实验室, 浙江 杭州 310018; 2.浙江理工大学龙港研究院, 浙江 温州 325802)
纱线属于高分子聚合物,具有弹性固体和黏性流体的特性[1]。纺织品生产过程中,纱线在张力作用下纤维内大分子皱曲状态伸展和纤维之间的滑移造成纱线内应力和应变的改变,从而影响纱线强力,对纺织品质量产生重要影响[2-3],因此,对纱线蠕变理论具有一定的研究价值。
当前,已有不少学者对纱线蠕变模型理论进行研究。GAO[4-5]以Burgers四原件模型对纱线蠕变进行了分析,证明了该模型符合纱线蠕变结果的拟合。王新威等[6]对纤维进行蠕变试验,证明了多项式回归方法对纱线蠕变性能测试的有效性。ASAYESH等[7]使用三元件模型,证明了该模型适用于织物的蠕变特性。高傑[8]以Riemann-Liouville型分数阶微积分理论构建了分数阶导数的Burgers蠕变模型,有效预测了红黏土的蠕变过程。梁娜等[9]构建了变参三元件模型,求解了聚合物基复合材料的蠕变。MASOUMI等[10]以整数阶M‖N模型预测了复合材料的蠕变。张思成等[11]以改进Burgers模型,通过试验得到了材料蠕变柔量和松弛模型的换算关系。目前用分数阶微积分理论对纱线蠕变模型研究的鲜有报道。
传统的纱线蠕变模型大多为整数阶模型。由于整数阶模型对纱线蠕变非线性问题的适应性差,且精度较低,因此,文本采用分数阶微积分理论建立纱线蠕变模型。为此,本文首先引用分数阶微积分理论,建立了纱线的非线性分数阶M‖N蠕变模型;然后通过纱线蠕变实验,获得纱线蠕变全过程曲线;最后,对纱线蠕变实验曲线进行拟合和预测,验证本文模型的准确性。
1 基于分数阶导数的纱线蠕变模型
1.1 预加张力恒定纱线松弛模型
目前,分数阶微积分有比较广泛的定义方式,为了有效描述纱线蠕变过程,本文采用Riemann-Liouville型分数阶微积分理论[12]。分数阶微积分定义为
(1)
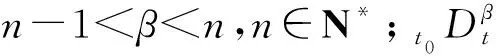
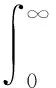
(2)
当0<β<1时,分数阶微积分算子经Laplace变换为
(3)
式中:s为Laplace变换参量;F(s)为f(t)的Laplace变换方程。
把纱线看作是由纤维经过牵伸-加捻后形成的软体元件,其基于Riemann-Liouville型分数阶理论的本构方程为
(4)
式中:τ(t)为纱线应变,%;u(t)为施加张力,cN;ξ为黏弹性系数,GPa。
当β=0时,令黏弹性系数ξ等于弹性模量E,则式(4)为弹性固体材料分数阶本构方程;当β=1时,令黏弹性系数ξ等于黏滞系数η,则式(4)为牛顿黏体分数阶本构方程;多数情况下,当0<β<1时,式(4)可以用做为介于牛顿黏体和弹性固体之间软体元件纱线的分数阶本构方程。
当u(t)为常量时,则式(4)描述为纱线蠕变模型。对式(4)进行Laplace正逆变换,得到基于Riemann-Liouville型分数阶理论的纱线蠕变模型:
(5)
式中,u为纱线蠕变量。
本文将Maxwell模型和Newton体进行并联,并且将黏壶元件以分数阶微分理论进行改进,建立了三元件分数阶纱线M‖N蠕变模型,如图1所示。

图1 分数阶 M‖N 纱线蠕变模型Fig.1 Fractional order M‖N yarn creep model
(6)
(7)
式中:τ为模型蠕变量;τM和τN为分数阶Maxwell体和分数阶Newton体的应力,cN;uM和uN为分数阶Maxwell体和分数阶Newton体的位移,mm;E1为弹性模量,GPa;η1和η2为模型黏滞系数;D1和D2为分数阶微分算子,且D1=dβ1/dtβ1,D2=dβ2/dtβ2。
将上述方程联立,可得纱线的分数阶本构方程:
(8)
对纱线本构方程式(8)进行Laplace变换,令u(t)=u0H(t)(H(t)为阶跃函数),则纱线蠕变的表达式为
(9)
式中:u0为纱线初始伸长,mm;u0=u(t)|t=0在纱线蠕变过程中为定值,则纱线蠕变方程为:
τ(t)=G(t)·u0
(10)
式中,G(t)为纱线蠕变模量,GPa。由式(9)、(10)可得纱线蠕变量的Laplace变换式:
(11)
为了得到纱线蠕变模量的Laplace逆变换,我们把M-L函数引入式(11)中然后对其进行Laplace正变换和逆变换,其中M-L函数[12]定义为:
(12)
式中:α、γ、k为M-L模型的参数;z为模型自变量。
式(12)的Laplace变换为
(13)

由式(11)、(13)可得,当式(13)中k=0,γ=1,α=β1时,n=E1/η1,纱线蠕变模量为
于是由式(10)、(14),得到纱线蠕变方程:
(15)
式中纱线弹性模量E1、模型黏滞系数η1、η2和分数阶阶数β1、β2,由纱线蠕变实验结果经过回归分析后得到。
1.2 预加张力变化时纱线蠕变模型
式(15)为拉伸载荷恒定时纱线蠕变模型,其模型内部参数随着施加张力的变化而变化。在实际生产中纱线的张力呈动态变化,因此,需考虑纱线张力的变化对纱线蠕变的影响。
根据纱线的应力-应变曲线的变化特征可知,纱线的蠕变量与施加张力的大小近似呈现出指数变化趋势。同时,对纱线施加载荷和蠕变曲线进行拟合,结果表明:纱线蠕变方程(15)中纱线的弹性模量E1,模型黏滞系数η1、η2,分数阶阶数β2和纱线施加载荷u为近似指数变化关系,而分数阶阶数β1不随纱线施加载荷u的变化而变化,可将其看做常量。另外,纱线在施加载荷时,将施加载荷量后纱线伸长量定义为初始伸长τ0=τ(t)|t=0,它也与施加载荷的值也呈现指数变化关系。于是,可建立如下考虑载荷影响的纱线蠕变分数阶M‖N模型。
式中:各参数由纱线蠕变实验结果通过cftool工具箱进行非线性拟合确定。
2 纱线蠕变实验
2.1 实验材料
纱线蠕变实验试样分别选用线密度为14.5、19.4、27.0和32 tex 4种不同线密度的棉纱。
2.2 蠕变装置及实验方法
实验采用XL-2型纱线强伸度仪测量纱线张力的变化,并通过数据采集系统实时监测。本文采用2种实验方法,实验1为4种不同线密度的纱线在张力恒定状态下的蠕变实验;实验2为张力不同时对线密度为19.4 tex纱线的蠕变实验。实验为温度20 ℃、湿度为65%,实验纱线长度为100 mm、采样时间间隔为1 s,时间从t=0时开始计时,张力加载时间为30 min。
2.3 实验结果处理
通过纱线蠕变实验得到纱线加载全过程蠕变曲线,图2示出不同线密度纱线以恒定张力100 cN测试的蠕变实验结果,图3示出不同张力时19.4 tex纱线蠕变实验结果。纱线蠕变的微观机制是由纤维间的滑移和纤维断裂引起的纱线结构调整。对于蠕变实验,后一载荷加载产生的蠕变量包括前一载荷加载产生的蠕变,因此,采取“坐标平移法”对纱线蠕变结果进行处理。
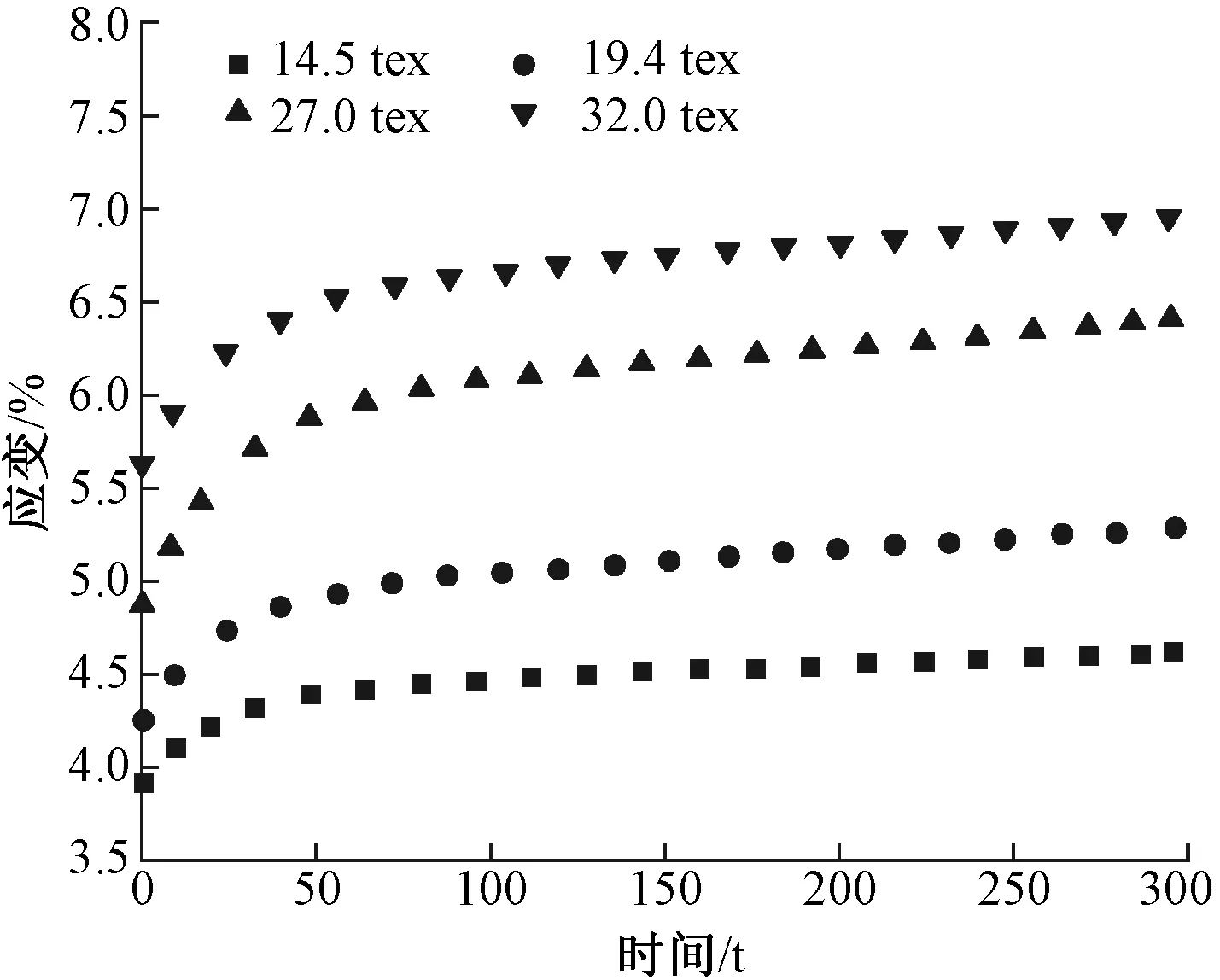
图2 不同线密度纱线蠕变实验结果Fig.2 Creep test result of yarn with different linear densities
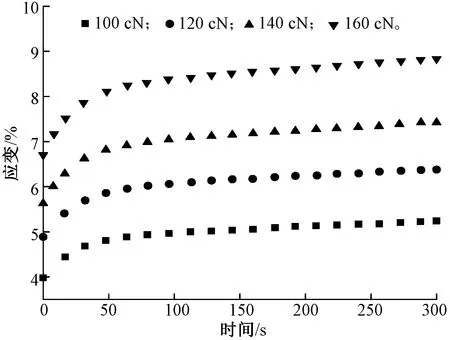
图3 不同拉力纱线蠕变实验Fig.3 Creep tests of cotton yarn with different tensile forces
由图2、3可知,纱线蠕变时在初始时刻处于弹性变形阶段,应变较大呈指数变化关系,之后趋于平缓在100 s时基本平衡。并且纱线线密度越大,应变也越大。
2.4 结果模型参数的确定
以实验1中纱线蠕变实验结果为例,来说明分数阶模型的建立过程与模型参数的确定。
首先,用纱线蠕变方程(15)对实验1不同线密度纱线蠕变曲线通过cftool工具箱进行拟合,如图4所示。然后,由拟合结果得到模型参数和相关系数,见表1,由此得到蠕变模型参数与施加张力大小的关系曲线,如图5所示。再将其进行回归分析,得到纱线蠕变模型参数和施加载荷大小变化的数学模型。因此,实验1纱线蠕变模型为:

图4 分数阶M‖N纱线蠕变模型对实验1的拟合曲线Fig.4 Fractional order M‖N fitting curve of yarn creep model to test 1
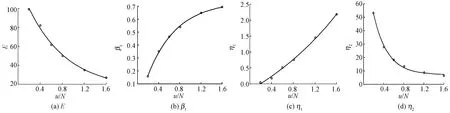
图5 实验1的模型参数与施加载荷的关系Fig.5 Relationship between model parameters and applied loads in test 1
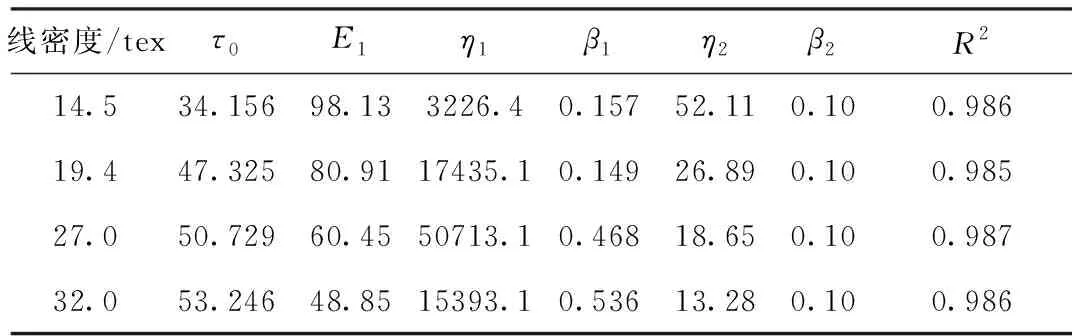
表1 分数阶M‖N纱线蠕变模型对实验1的拟合结果Tab.1 Fitting results of fractional order M‖N yarn creep model to test 1
按照上述求实验1不同线密度纱线蠕变模型方法和步骤,对实验2中不同载荷下对应的纱线蠕变曲线进行回归分析,即得到实验2不同张力下的纱线蠕变模型:
(18)
模型参数和相关系数R2如表2所示。拟合结果如图6所示。

图6 分数阶M‖N纱线蠕变模型对实验2的拟合效果Fig.6 Fitting results of fractional order M‖N yarn creep model to test 2
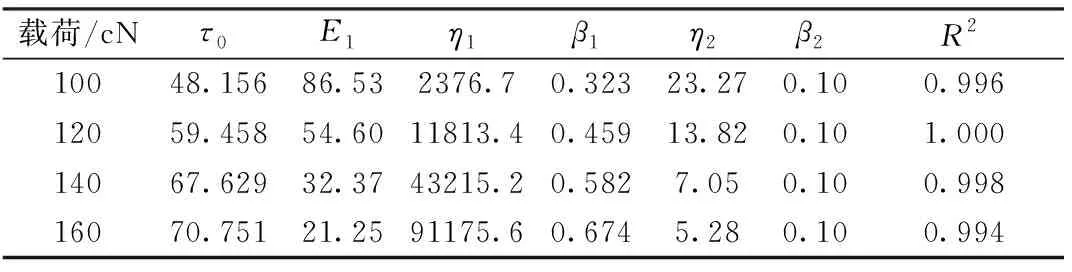
表2 实验2的参数拟合结果Tab.2 Fitting results of test 2
3 模型对比分析
为了证明本文模型的合理性和可靠性,将本文模型与三元件模型、整数阶M‖N模型和Burgers模型进行对比。
3.1 模型拟合效果
以实验2不同载荷纱线蠕变结果为例,选用载荷为100 cN和120 cN对应的纱线蠕变曲线进行回归建模,将140 cN和160 cN对应的纱线蠕变曲线做预测对比分析。以本文1.3节的建模方法,获取三元件模型、整数阶M‖N模型和Burgers模型的纱线蠕变模型、拟合曲线、模型参数以及模型的相关系数,并进行比较。这里只对各模型纱线蠕变曲线的拟合精度进行对比分析,如图7所示。

图7 不同模型对实验2拟合效果曲线Fig.7 Fitting effect curves of different models to test 2
从图7可以看出,整数阶三元件模型对纱线蠕变拟合精度最差、Burgers模型次之、整数阶M‖N模型较好、本文模型对纱线蠕变拟合精度最高。整数阶M‖N模型的拟合精度较高,但在纱线蠕变拐点位置的误差较大。为了更能说明本文模型对纱线非线性蠕变特性的精度,还以实验2中各载荷的拟合和实际实验结果的均方差(SSE)和相关系数作为拟合精度评价指标,如表3所示。

表3 实验2的模型拟合精度评价Tab.3 Model fitting accuracy evaluation for test 2
由表3可知,本文模型的均方差最小,相关系数R2最大,说明本文提出的分数阶M‖N模型对纱线蠕变模型的拟合效果优于三元件模型、整数阶M‖N模型和Burgers模型。分析表明,分数阶M‖N模型能够很好的反应纱线蠕变的全过程,并且模型拟合精度高、模型简单。
3.2 模型预测结果分析
对实验2中线密度为19.4 tex,张力为100、120、140、160 cN对应的纱线蠕变曲线进行回归分析,分别得到本文模型、三元件模型、整数阶M‖N模型和Burgers模型所对应的纱线蠕变模型。接下来,对120 cN和160 cN对应的纱线蠕变曲线进行预测,如图8所示。并且对纱线蠕变预测结果进行误差分析,如表4所示。

表4 模型拟合精度评价Tab.4 Model fitting accuracy evaluation
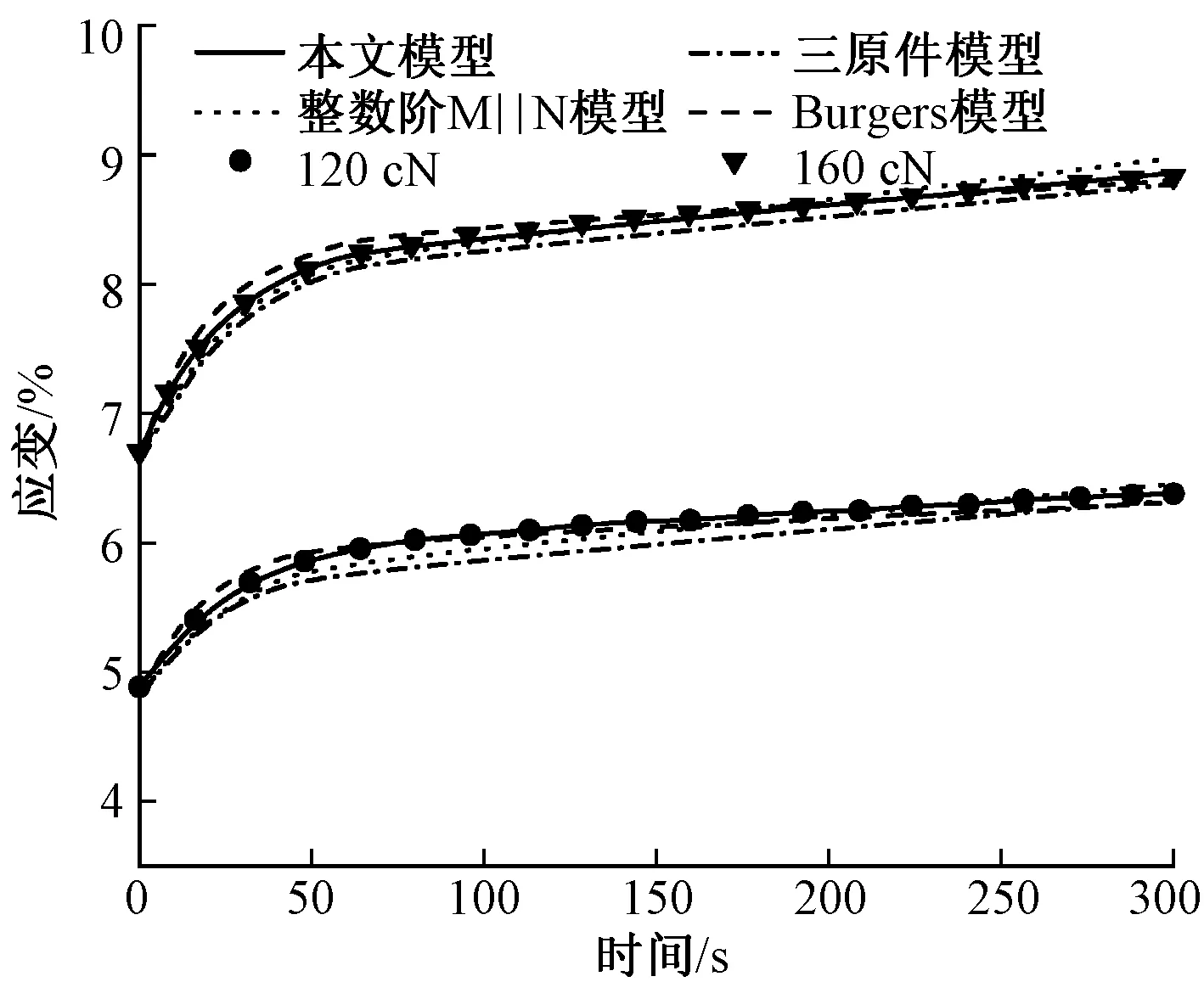
图8 不同模型对实验2纱线蠕变的预测Fig.8 Prediction of yarn creep by model under different tension in Test 2
由图8可知,本文提出的分数阶M‖N纱线蠕变模型预测效果最好,其次为整数阶M‖N模型,最后为三元件模型和Burgers模型。此外,本文分数阶M‖N纱线蠕变模型预测结果的MSE最小,相关系数最大,进一步说明了分数阶M‖N模型对纱线蠕变的预测效果优于其他3种模型。综上所述,本文建立的分数阶M‖N纱线蠕变模型,不仅对纱线蠕变结果的拟合精度较高,而且具备较高的纱线蠕变预测能力。
4 结 论
为了深入研究纱线蠕变特性,通过实验得到不同载荷和不同线密度的纱线蠕变全过程曲线。基于分数阶微积分原理,以软体元件替换传统牛顿黏体元件,建立一种新的纱线蠕变模型。构建的分数阶纱线蠕变模型不仅结构简单,而且对纱线的蠕变行为能够很好的拟合和预测。对比三元件模型、整数阶M‖N模型和Burgers模型对纱线蠕变的拟合和预测,可以看出,本文建立的三元件分数阶M‖N纱线蠕变模型在表达纱线蠕变方面具有模型参数少、精度高的特点。研究结果为纱线蠕变行为分析提供了理论参考。

