基于全连接神经网络的旋挖钻机缓冲平衡阀故障诊断
闻 岩, 徐 俊, 高 伟, 陈立娟, 常明明, 艾 超
(1.燕山大学机械工程学院, 河北秦皇岛 066004; 2.南京工程学院机械工程学院, 江苏南京 211167)
引言
旋挖钻机是机电液集成程度很高的大型工程机械设备。其主要结构包括行走系统、工作系统和回转系统。缓冲平衡阀在旋挖钻机的回转系统中处于核心地位,缓冲平衡阀性能的好坏直接影响整机的工作平稳性,回转定位精度和钻孔的质量[1]。旋挖钻机工作环境恶劣,油液中时常会有大颗粒污染物。带有污染颗粒的高压油液在液压系统中流动时会对各个部件造成严重损害。其中,缓冲平衡阀的阀芯在高压油液冲击下会快速磨损,导致阀芯和阀套的间隙增大,平衡阀的内泄漏增大,对旋挖钻机工作的平稳性,可靠性和系统效率产生一定影响。此时,旋挖钻机回转系统旋转时响应会滞后,直接的表现是旋转启动变慢和旋转制动变慢。平衡阀的故障信息通常比较微弱,故障特征难以提取。因此对缓冲平衡故障诊断进行相关研究,对于旋挖钻机提升安全性和工作效率具有重大意义。
国内外学者针对液压阀故障诊断进行了大量研究。权凌霄等[2]采用“GA+LM”优化BP神经网络的方法,提升了网络的学习速度和精确搜索能力,进而大幅提高了基于BP神经网络的电液伺服阀故障诊断的效率和精度,实现了电液伺服阀阀芯一端限位、一侧固定节流孔堵塞、阀芯磨损、阀芯零位不对中等故障的诊断。邱寒雨等[3]提出了一种基于BP神经网络和AdaBoost算法的故障诊断方法,对快速起竖装置的液压驱动系统建立了故障模型,实现了其常用工况下的故障诊断。杜名喆等[4]针对液压泵振动信号的非平稳性的特点,提出了一种基于小波变换和卷积神经网络的算法,实现了液压泵的自动故障诊断。王磊等[5]首先建立对应的电液伺服阀的液压仿真模型,再通过修改模型的参数,人为制造故障并提取了故障特征信息,最后应用PCA-SVM的方法对伺服阀的一端限位、喷嘴堵塞和力矩马达磁性减弱等故障进行分类。贾春玉等[6]构建了CNN+LSTM相结合的故障预测模型,取代了人工特征选取和提取,解决了故障预测的时序问题,实现了电液伺服阀阀芯磨损和阻尼孔堵塞的故障诊断。王巧云[7]提出了GA-BP网络模型,该算法既具有较强的局部搜索能力和非线性映射能力,又具有全局搜索能力,解决了电液伺服阀的故障模式识别问题。沈晨晖等[8]针对电液伺服系统非线性程度高、状态参数较多等特点,提出将SR-CKF应用于电液伺服系统的状态估计之中。杨东[9]以力反馈两级电液伺服阀为研究对象,提出了基于测试信号的电液伺服阀智能故障诊断算法研究。LIU Chao等[10]提出了一种基于极限学习机的故障诊断模型来区分电液伺服阀的故障。SHI Jinchuan等[11]提出了一种两阶段多传感器信息融合法,包括故障特征融合和决策信息融合,实现了对液压阀的故障诊断。JI X等[12]针对液压阀结构封闭复杂的特点,提出了一种基于Dempster-Shafer理论的故障诊断方法,对液压阀的几种特定故障实现了检测。上述方法对本研究解决缓冲平衡阀故障诊断问题提供了一定的方向性。
由于平衡阀的可变节流边是有倒角的,且阀芯阀套配合间隙较大,同时平衡阀结构复杂,里面有多个阻尼孔,且旋挖钻液压系统油液污染度较大,因此旋挖钻用平衡阀故障难以诊断。平衡阀的工况比较单一,故本研究以额定工况下的旋挖钻用平衡阀为研究对象,揭示平衡阀故障机理,针对故障数据难以获得的问题,进行平衡阀加速退化实验,获取故障数据,将采集的数据按一定比例分为测试集和训练集。然后,结合全连接神经网络方法,将训练集数据导入全连接神经网络模型中进行训练。最后,将测试集数据导入神经网络模型中,对模型精度进行验证。
1 缓冲平衡阀的故障机理分析及动力学建模
本研究的缓冲平衡阀的液压原理图如图1所示,V2,V1为进出油口,C2,C1口外接负载。V2口进油时,油液通过单向阀到达C2口,然后进入外接负载,再流入C1口并通过右边的平衡阀,并经过单向阀,最后从V1口流出。右边的平衡阀是由先导油路a和自身的先导共同作用打开的。

图1 缓冲平衡阀液压原理图Fig.1 Hydraulic schematic diagram of buffer balance valve
缓冲平衡阀是具有对称结构的双向平衡阀,在外接负载正转、反转和制动时都能起到减小冲击的作用[13],该缓冲平衡阀的结构原理图如图2所示。正转时,当压力油从V2流入、V1流出时,对阀芯A进行动力学分析,其动力学方程为:
(1)
(2)
制动时,压力油直接作用在阀芯A上,阀芯A的动力学方程为:
(3)
式中,p1—— 负载端进油口压力
p2—— 负载端出油口压力
SA—— 右侧阀芯有效受力面积
SB—— 左侧阀芯有效受力面积
F1—— 右侧弹簧预紧力
F2—— 左侧弹簧预紧力
m1—— 右侧阀芯质量
m2—— 左侧阀芯质量
BV—— 黏性阻尼
k1—— 右侧弹簧刚度
k2—— 左侧弹簧刚度
x1—— 右侧弹簧位移
x2—— 左侧弹簧位移

图2 缓冲平衡阀结构原理图Fig.2 Structure schematic diagram of buffer balance valve
针对旋挖钻机缓冲平衡阀,其主要机械故障形式有阀芯磨损、卡滞、密封件损坏和油污等[14],其中阀芯磨损故障最为常见,本研究正是对缓冲平衡中的平衡阀阀芯的磨损故障展开研究,缓冲平衡阀的平衡阀阀芯如图3所示。

图3 平衡阀阀芯Fig.3 Balance valve spool
阀口流量压差方程为:
(4)
式中,q—— 流量,L/min
Cd—— 流量系数
A—— 过流面积,m2
Δp—— 进出口压差,Pa
ρ—— 油液密度,kg/m3
系统的流量q为常数不变,由于阀芯的磨损,过流面积A变大,而流量系数Cd和油液密度ρ为常数不变,因此平衡阀进出口B,T压差Δp变小。因此,可以以进出口压差作为神经网络的输入,以平衡阀的磨损故障特征标签作为输出,来实现平衡阀磨损故障的在线诊断。
2 缓冲平衡阀加速退化实验及模型验证
2.1 实验方案设计
平衡阀长时间工作在高压油液中,受到高压油液中的污染颗粒的不断冲击,对阀芯的工作棱边产生冲蚀磨损;阀芯、阀套的径向间隙会受到尺寸与径向间隙尺寸相近的颗粒物的摩擦磨损。棱边磨损与径向间隙磨损,均会导致内漏量增加与压力增益的降低,且油液的污染磨损这两个性能指标影响较明显。因此,选择B,T口压力差作为平衡阀污染磨损加速退化试验的性能退化参数。由于平衡阀的价格昂贵,试验样本量有限,综合考虑试验的可行性与效费比,本试验选用加速退化试验方式。
缓冲平衡阀加速退化实验不同于伺服阀加速退化实验,伺服阀对油液污染度较为敏感,在油液中加入一定的污染物可以使伺服阀加速退化。但是,缓冲平衡阀阀芯有较强的抗污染能力,在一定的时间内并不能达到理想的退化效果。由于时间有限,本实验将平衡阀阀芯取出进行手工均匀磨损。
2.2 故障数据获取
本实验采用的液压试验台如图4所示,可完成小流量伺服阀、平衡阀等液压阀类元件的静动态性能测试,根据平衡阀加速性能退化实验的要求,本次实验在测试车的基础上,设计适合做退化实验的液压油路、测试流程和测控系统。测试系统的泵为力士乐恒压定量泵,测试所用压力传感器量程均为0~25 MPa,系统压力由安全溢流阀和负载溢流阀控制,系统流量为固定值。

图4 试验台Fig.4 Test stand
回转缓冲阀加速退化实验的测试原理图如图5所示,测试所用实验台压力为20 MPa,流量为40 L/min。V2口连接P口,V1口连接T口,C2口连接A口,C1口连接B口,并在4个油口连接压力传感器。阀芯磨损实验:将阀芯取出用砂纸均匀磨损,然后测试B,T口压差,并采集相应数据,此过程重复多次。
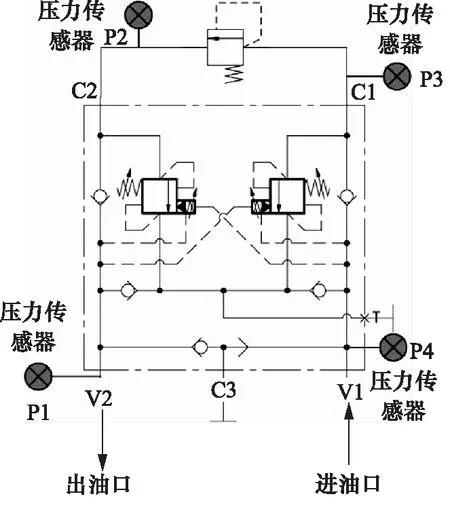
图5 液压原理图Fig.5 Hydraulic schematic
平衡阀阀芯正常和磨损的对比图如图6所示。
采集到的B,T口压差数据需要打上对应的标签,设置的标签如表1所示。

图6 对比图Fig.6 Contrast chart

表1 状态标签Tab.1 Status label
采集到的部分数据如表2所示,B口压力有一个逐步减小的趋势,而T口压力基本不变,Δp有逐渐减小的趋势,故障标签由卡滞故障到正常然后到磨损故障的一个过渡。由式(4)可知,过流面积A变大,Δp则变小,而数据1到数据10过流面积在逐步增大,因此Δp有逐步减小的趋势。

表2 实验数据Tab.2 Experimental data
3 基于全连接神经网络模型的故障诊断
3.1 全连接神经网络模型
全连接神经网络是最基本的神经网络结构,一般包括输入层、隐含层和输出层,1个全连接网络中只有1个输入层和1个输出层,但可以包含多个隐含层,层与层之间的神经元都相互连结。全连接神经网络理论上可以拟合任何函数,同时对非线性的函数拟合效果很好,隐藏层数越多,其网络表达能力越强。图7是1个2层的全连接神经网络,上一层为下一层的输入层,其计算过程的本质是矩阵运算,主要由前向传播运算和反向传播运算组成。

图7 全连接神经网络Fig.7 Fully connected neural network
1) 前向传播
如图7所示,前向传播即输入数据经过输入层、隐藏层最后到输出层的传播过程。其中,神经网络输入数据的向量表达式如式(5)所示:
(5)
输出向量表达式如式(6)所示:
(6)
设第l层神经元的输出如式(7)所示:

j=1,2,…,sl
(7)
则第l层的输出表达式如式(8)所示:
(8)
由上述可得每层神经元的输出可以表示为该层神经元的输入乘以1个权重再加上1个偏置项,如式(9)所示:
h(l)=f(WH+B)
(9)
式中,f() —— 激活函数



B—— 每层网络的偏置矩阵
W—— 每层网络的权重矩阵
H—— 神经网络的输入
神经网络模型往往要加入一定的非线性因素(即激活函数),以解决模型非线性拟合能力的不足,引入激活函数后单个神经元的计算过程如图8所示。

图8 单个神经元计算过程Fig.8 Single neuron computing process
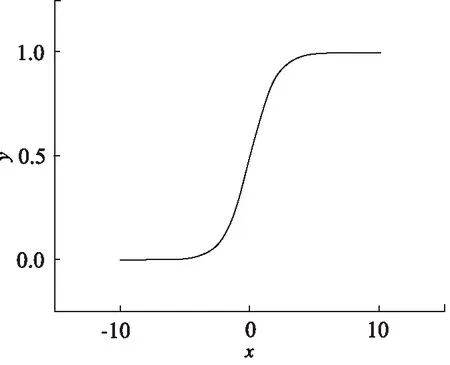
图9 Sigmoid函数图像Fig.9 Sigmoid function image
目前常用的非线性激活函数有Sigmoid函数、Tanh函数和ReLU函数[15],函数图像及其对应公式如下所示:
Sigmoid(x)=1/(1+e-x)
(10)
Tanh(x)=(1-e-2x)/(1+e-2x)
(11)
ReLU=max(0,x)
(12)
2) 反向传播
神经网络模型中的参数分为模型参数和模型超参数,模型参数需要训练,模型超参数由人为指定。网络模型的训练过程其实是对模型参数进行训练,从而使模型误差达到一个满意的范围。

图10 Tanh函数图像Fig.10 Tanh function image

图11 ReLU函数图像Fig.11 ReLU function image
在全神经网络的计算中,输入层经过隐含层计算再到输出层输出结果, 这一过程称为前向传播。前向传播过程模型参数并未得到训练, 所以必须得通过反向传播过程来训练模型参数,使模型的误差达到可接受的范围。输出层的输出结果和实际值有一定偏差,利用损失函数估算误差值,再由损失函数得到代价函数,最后用迭代公式更新训练模型的模型参数-权重参数w和偏置参数b。损失函数、代价函数、迭代公式如式(13)~式(16)所示:
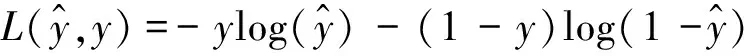
(13)
(14)
(15)
(16)
式中,L—— 损失函数
J—— 代价函数
y—— 实际值

w—— 权重
b—— 偏差
m—— 样本个数
α—— 学习率
3.2 模型的搭建
该故障诊断模型是在PyCharm中利用Python语言基于Tensorflow深度学习框架编写的。具体实现步骤如下:
(1) 导入实验获取的故障数据;
(2) 随机打乱数据,将数据以2 ∶1的比例分为训练集和测试集;
(3) 将数据类型转换为统一的浮点型,保证矩阵运算不会出错;
(4) 利用Sequential来设置神经网络结构;拉直层:变换张量的尺寸,把输入特征拉直为一维数组;中间层(全连接层):设置中间层神经元数目为128,激活函数选择ReLU函数;输出层(全连接层):设置输出层神经元数目为5,激活函数选择softmax函数;
(5) 利用Compile来配置神经网络的训练方法,设置训练时使用的优化器为adam,损失函数选择计算交叉熵损失函数,准确率评测标准选择sparse_ categorical_accuracy,以数值形式给出标签,以概率分布形式表示输出。
(6) 使用fit来执行训练过程。将测试集数据和对应的标签,每次喂入模型4组数据,迭代计算100次,每迭代一次输出一次准确率;
(7) 设置文件保存路径,保存模型参数,保留最优结果;
(8) 绘制训练准确率、测试准确率、训练损失和测试损失曲线。
模型各层参数设置如表3所示。

表3 模型参数Tab.3 Model parameter
3.3 故障诊断的实现
基于全连接神经网络的故障诊断实现过程如图12所示。首先,将原始数据通过实验采集回来之后进行预处理导入Excel表格中;然后将数据随机打乱,将训练集和测试集的数据量按照2∶1划分,并将数据打上故障标签;最后,编写全连接神经网络的代码,将打好标签的训练数据导入模型中进行训练,模型训练好之后用测试集来验证模型的准确度。
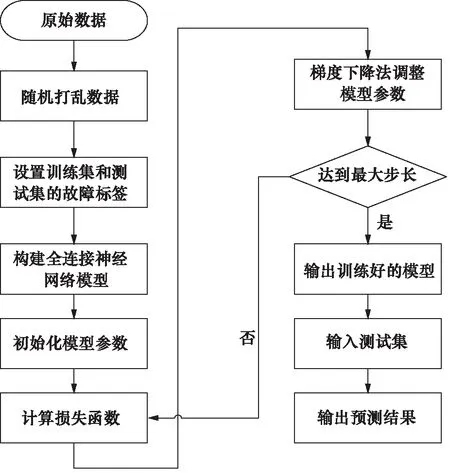
图12 故障诊断实现流程图Fig.12 Flow chart of fault diagnosis implementation
3.4 模型训练及验证
将采集到的数据进行上图12所示处理,数据导入模型中进行训练后,将该神经网络模型的训练集准确率曲线、loss曲线和测试集准确率曲线、loss曲线进行输出,如图13所示。横坐标是迭代次数N,纵坐标分别是准确率η和损失值L。准确率可以衡量模型精度,损失值衡量模型预测值和真实值的差距。可以看出该模型的准确率随着迭代次数的增高逐渐增大,损失值随着迭代次数的增高逐渐减小,该模型最终的准确率为92%。
4 结论
以缓冲平衡阀为研究对象,构建了基于全连接神经网络的缓冲平衡阀的故障诊断模型,取代人工特征选择和提取,在特定工况下对平衡阀故障的识别与诊断具有较高的准确性。使用加速退化实验所得的B,T口压差故障数据集验证该模型的有效性。结果表明,该模型取得了较好的诊断效果,准确率高达92%。

