二维柱塞泵扭矩特性分析

赵文亮, 朱登魁, 阮 健, 徐 钰, 周洪学, 黄帅宗

(1.河南航天流体控制技术有限公司， 河南郑州 451191； 2 浙江工业大学， 浙江杭州 310014；3.河南航天液压气动技术有限公司， 河南郑州 451191)

引言

滚轮固定式二维柱塞泵由于本身结构的原因，装配中不可避免地存在导轨轴向间隙。目前的机械结构采用弹簧预紧的方式消除轴向间隙[1-3]。在装配实践中发现存在弹簧预紧力的二维柱塞泵，其扭矩普遍大于无预紧弹簧结构；且随着弹簧预紧力的增加，二维柱塞泵扭矩也随之增加。根据二维柱塞泵结构特点，理想状态下弹簧预紧力的大小对二维柱塞泵扭矩无影响。因此，本研究致力于探究弹簧预紧力的大小对于二维柱塞泵扭矩作用机理的影响，从而进一步完善二维柱塞泵设计理论。

1 扭矩特性分析

二维柱塞泵泵芯总成典型结构如图1所示，二维柱塞泵通过缸体与柱塞上对称开的4个配油口，通过柱塞的转动实现配油机能。随着柱塞的旋转，缸体上配油口与柱塞上开槽周期性的开合，其工作原理[4]如图2所示。

泵芯沿逆时针方向旋转，同时在滚轮的作用下做轴向往复运动。活塞上与缸体右腔相通的腔记为腔1，活塞上与缸体左腔相通的腔记为腔2。图2a位置时，滚轮位于凸轮最低点(以左边滚轮为例)，活塞与缸体上油口不连通，随后活塞在滚轮、凸轮的作用下向左运动。缸体右腔容积逐渐变大，腔1此时与缸体的吸油口连通，右腔开始吸油；同时，缸体的左腔容积逐渐减少，腔2与排油口连通，左腔开始排油，如图2b位置所示。

图2c位置时，滚轮到达凸轮最高点(以左边滚轮为例)，活塞与缸体上油口不连通，随后活塞在滚轮、凸轮的作用下向右运动。缸体右腔容积逐渐变小，腔1此时与缸体的排油口连通，右腔开始吸油；同时，缸体的左腔容积逐渐变大，腔2与吸油口连通，左腔开始吸油，如图2d位置所示。

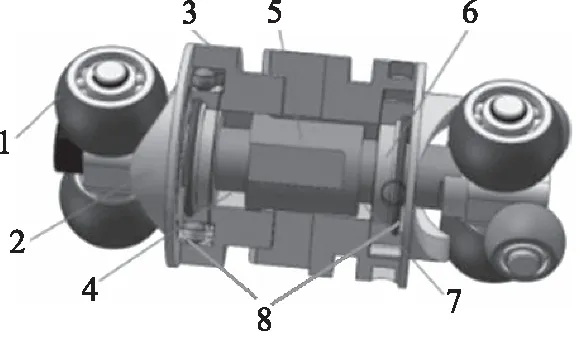
1.滚轮 2.导轨 3.缸体 4.左腔 5.柱塞 6.同心环 7.右腔 8.波形垫圈图1 泵芯总成Fig.1 Pump core assembly

图2 二维柱塞泵配油机理Fig.2 Two-dimensional piston pump working principle

活塞继续旋转，在滚轮、凸轮的作用下继续向右运动，滚轮达到凸轮最低点(以左边凸轮为例)，腔1、腔2与缸体上配油口间均为关闭状态，完成一个循环，如图2e位置所示。

导轨是二维柱塞泵的关键零件，导轨的设计可借鉴圆柱凸轮机构。凸轮机构是使从动件作预期规律运动的高副机构[5]，其主要优缺点如下：

优点是从动件的运动规律可以任意拟定，其运动时间与停歇时间的比例以及停歇次数都可以任意拟定；缺点是高速凸轮机构中，其高副接触处的动力学特性比较复杂，精确分析与设计都比较困难。

前期研究表明，具有等加等减运动特性的转子组件，双联设计能够有效降低二维柱塞泵压力脉动[6-9]，因此采用等加等减曲线设计二维导轨。

等加速等减速运动规律，Am最小，但即使在无停歇的运动中仍有柔性冲击，行程始末及中点加速度出现突变(即Jm→∞)，要求机构刚度大及系统间隙小；在耐磨损、压力角、弹簧尺寸等方面不如简谐和摆线规律，目前很少用。等加速、等减速段周期及行程分别为β1，h，加速段和减速段范围分别为(0～1/2β1，0～1/2h)和(1/2β1～β1，1/2h～h)。轴向位移函数分别如式(1)[6]、式(2)：

S=2h(θ/β1)2

(1)

(2)

二维导轨的设计取π/2作为1个周期，柱塞旋转1周完成4个周期。柱塞输入轴匀速转动，根据等加等减速曲线方程得式(3)、式(4)(以下公式推导，除特殊说明外，物理量单位皆为国际单位)：

(3)

β1=π/2

(4)

其中：θ—— 导轨转动角度

ω—— 导轨转动角速度

t—— 时间

β1—— 运动周期

则，转子组件轴向位移方程为：

(5)

式中，S—— 转子组件轴向位移

h—— 导轨高程

将式(3)代入式(5)得：

(6)

S(θ)对θ求导：

(7)

图3 导轨-滚轮受力分析Fig.3 Cam-idler wheel force analysis

二维导轨曲面为具有2个波峰/波谷的马鞍面。以泵芯总成的转子组件为研究对象进行空载工况下的受力分析，如图3所示，此时导轨与滚轮的作用力完全由作用于导轨下的弹簧预紧力产生(忽略重力影响)，此结构中的弹簧预紧力由波形垫片的压缩产生。图中，Fbr，Fr为导轨对滚轮支反力的轴向、径向分力。柱塞转向如箭头所示，从下往上看，柱塞沿逆时针方向转动，滚轮位于π/4位置。

如图3所示，Fbr完全由作用在导轨上的弹簧预紧力提供，大小等于弹簧预紧力，可得：

Fbr1=Fbr2

(8)

将导轨曲面上中心线沿周长展开及受力分析，如图4所示。图中，Fc为导轨对滚轮的作用力；v为滚轮与导轨接触点的矢量方向；α为导轨压力角；Rb为导轨曲面中径。

由图3可知：

(9)

根据机械设计手册凸轮机构的设计[5]可知，压力角为：

(10)

(11)

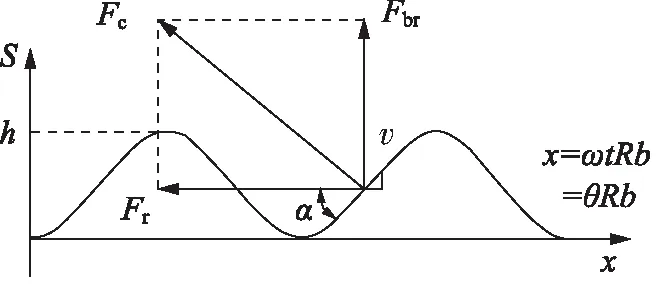
图4 导轨曲面中线沿圆周方向展开及受力分析Fig.4 Extend wings of cam facemiddle line and force analysis

对于圆柱凸轮，e=0(e为偏心距)，将式(7)、式(11)代入式(10)可得：

(12)

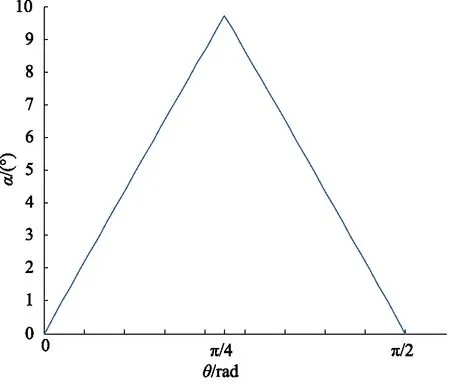
图5 滚轮转动角度-压力角关系曲线Fig.5 Idler wheel angle-pressure line

将h=4 mm，Rb=29.75 mm代入式(12)得压力角曲线如图5所示。由图5可知，压力角在滚轮转动角度(0～π/2)周期内，关于π/4对称；当上滚轮处于导轨π/2位置时，下滚轮处于导轨0位置；随着柱塞转动，上滚轮向导轨0位置运动，下滚轮向导轨π/2位置运动，且运动角度相等。因此，可认为上、下滚轮在导轨位置的压力角时刻相等，即：

α1=α2

(13)

由式(6)、式(7)和式(11)可得：

Fr1=Fr2

(14)

又由图2可得，Fr1，Fr2方向相反，作用点相对于圆心的距离Rb相等(也即力臂相等)，因此其对柱塞的扭矩大小相等，方向相反。因此，以泵芯为分析对象，弹簧预紧力为内力，对泵芯的输入扭矩无影响。

2 异常原因分析

由上节分析可知，以泵芯为分析对象，弹簧预紧力为内力，对泵芯的输入扭矩无影响。但实际装配过程中发现，随着弹簧预紧力的增大，输入扭矩急剧增大，与理论分析结论相反。为分析这一现象，对发生输入扭矩增大的二维柱塞泵泵芯结构进行深入分析。

如图6为泵芯剖面图，导轨、滚轮配合面为带一锥度的斜面，理论上，该斜面交点位于柱塞回转中心。同心环与柱塞之间为小间隙配合，配合间隙0.004～0.008 mm。理论上，当滚轮锥面、导轨锥面的交点位于柱塞回转中心时，弹簧预紧力不产生多余的外力，弹簧预紧力不影响泵芯的输入扭矩。

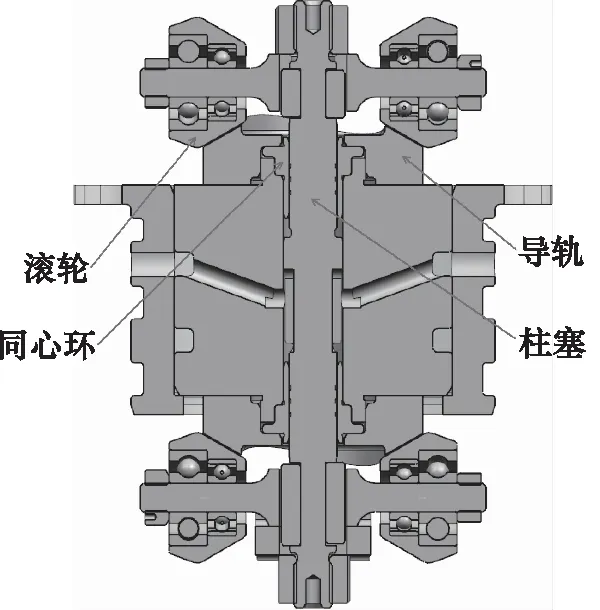
图6 泵芯剖面图Fig.6 Profile map of pump core

但实际装配过程中，为保证导轨、滚轮锥面的交点位于柱塞回转中心，需由多个零件的加工精度保证，包括导轨曲面的加工精度、导轨定位孔的加工精度、缸体的外圆精度、外圆与内孔的同轴度、滚轮的锥面加工精度、滚轮的装配精度6个相关形位公差来保证。尺寸链较长，将0.004～0.008 mm的公差带分配给6个尺寸，现有的加工能力无法保证。因此，必然导致导轨、滚轮锥面约束的柱塞回转中心与同心环约束的柱塞回转中心不重合，且两回转中心的距离远大于柱塞与同心环的配合间隙。反映在导轨-滚轮运动副即为一侧滚轮与导轨接触，产生作用于柱塞的径向力。在存在弹簧预紧力的情况下，随着弹簧预紧力的增大，摩擦力随之增大，进而导致输入扭矩增大。

3 验证工装设计及数据分析

基于上节的分析结论，为验证弹簧预紧力对二维柱塞泵扭矩特性的影响，提出如下假设：在排除同心环对柱塞摩擦力的影响下，弹簧预紧力的大小与二维柱塞泵输入扭矩的大小无关。

工程中可用参数检验的方法，从总体中随机抽取一定数量的样本进行研究，并以此推断总体。参数检验不仅能够对1个总体的参数进行推断，还能比较2个或多个总体的参数。

假设检验的基本思路是首先对总体参数提出零假设，然后利用样本的数据去验证先前提出的假设是否成立。如果样本数据不能充分否认零假设，则不能拒绝零假设。在假设检验的推断过程中，基本原则是依靠统计分析推断原理，即小概率时间在一次特定的抽样中几乎不可能发生，如果发生了小概率事件，就有理由拒绝零假设。

根据假设检验统计方法和本研究发现的理论现象的矛盾点，提出了上一假设。同时，为验证这一假设，设计了假设验证工艺装备，取消同心环结构，同时保留导轨、滚轮锥面。该工装设计有弹簧，弹簧位于保持架和缸体之间，安装完成后弹簧处于预压缩状态。然后以弹簧预紧力为自变量，采集不同弹簧预紧力下二维柱塞泵的扭矩值，计算弹簧预紧力对于扭矩影响的显著性水平(p值)。工程实践中常用p值为0.05，即当显著性水平大于0.05时，认为弹簧预紧力对二维柱塞泵扭矩无影响；当显著性水平小于0.05时，认为弹簧预紧力对二维柱塞泵扭矩有影响[10-12]。

3.1 工艺装备设计

基于上述工艺装备设计思想，设计了如图7所示工艺装备。该工艺装备的特点为：保留了导轨、滚轮的锥度结构，导轨与滚轮的受力与原结构相同；取消了同心环结构，柱塞与缸体间为大间隙，排除了摩擦力的影响。

同时为保证弹簧预紧力可调，设计了如图8所示的弹簧预紧结构，共对称布置8个预紧弹簧，改变预紧弹簧数量即可以改变二维柱塞泵预紧力大小。为充分说明试验结论的有效性，选取4个预紧弹簧结构(弹簧预紧力44 N)和8个预紧弹簧结构(弹簧预紧力88 N)2种工况作为自变量，采集不同角度下二维柱塞泵的扭矩，计算弹簧预紧力对于扭矩影响的显著性水平(p值)。

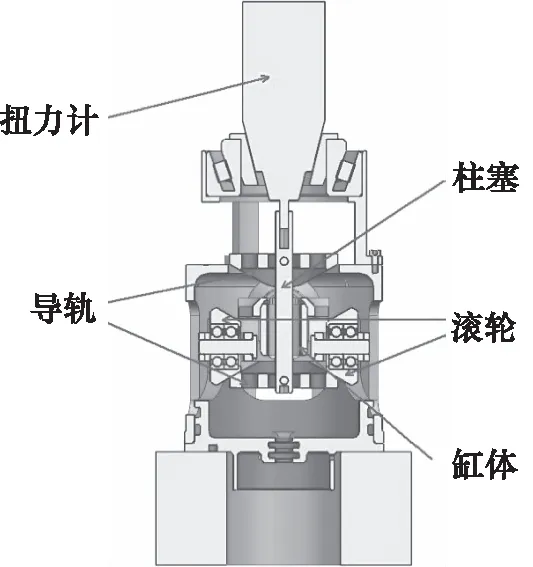
图7 弹簧预紧力验证工装Fig.7 Verify tool of spring preload

图8 预紧弹簧结构Fig.8 Spring preload structure

3.2 扭矩数据采集及分析

本研究设计了如图9所示的数据采集工装，分别用于采集4个预紧弹簧和8个预紧弹簧下不同角度处的二维柱塞泵扭矩。

本研究通过N·m级的扭力计采集泵芯扭矩。如图9所示，为便于测量不同角度下的输入扭矩，在扭力计座2上设计有刻度线。基于上图所示的扭矩数据采集工艺装备，分别采集了4个预紧弹簧结构(弹簧预紧力44 N)和8个预紧弹簧结构(弹簧预紧力88 N)，0°～40°下的泵芯输入扭矩，如表1所示。

使用假设检验分析方法和SPSS分析软件，计算检验的观测显著性水平(p值)。SPSS计算结果表明：显著性水平为0.867，远大于0.05，如表2所示。因此，可以认为弹簧预紧力对二维柱塞泵扭矩无影响。

图9 扭矩采集工装Fig.9 Torque measure tool

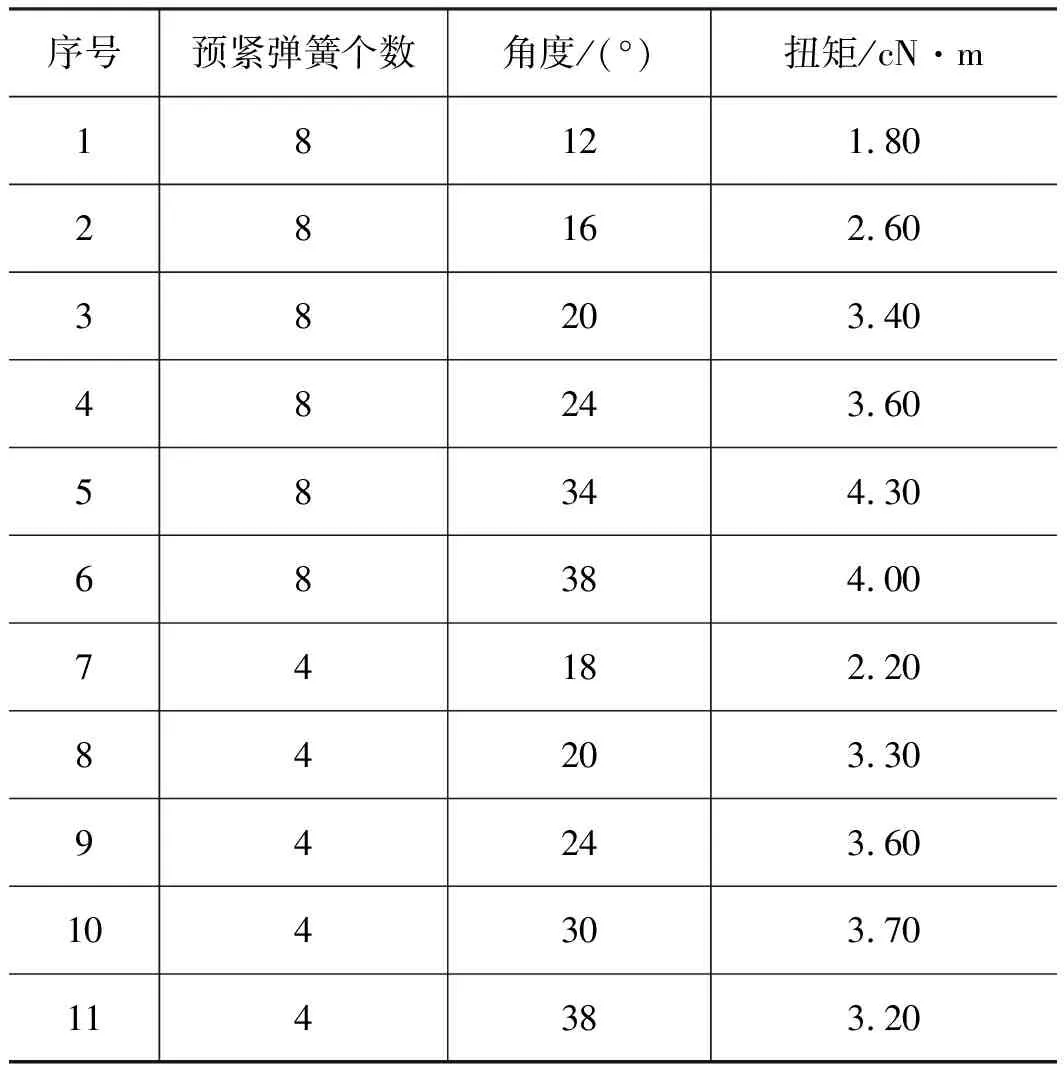
表1 扭矩采集数据表Tab.1 torque data of different angle

表2 显著性水平计算Tab.2 Significance level calculate

4 结论

(1) 综上所述，验证结果表明：理想情况下，弹簧预紧力对二维柱塞泵扭矩特性的无影响。弹簧预紧力增加造成二维柱塞泵扭矩增加的真实原因为：导轨、滚轮具有一定锥面时，加工、装配误差导致弹簧预紧力使柱塞相对于同心环产生了额外的法向力；当弹簧预紧力增大时，柱塞-同心环法向力增大，摩擦力增大，因此造成二维柱塞泵扭矩增大。

(2)进一步推广到负载工况，随着输出压力增加，柱塞-同心环之间的法向力将进一步增大，摩擦力增大。因此，导轨、滚轮具有一定锥面时，加工、装配误差导致柱塞-同心环间产生了额外的法向力，是降低二维柱塞泵机械效率的重要原因。