安装状态的O形橡胶密封圈非线性有限元分析
米雄伟
(1.中国煤炭科工集团太原研究院有限公司, 山西太原 030006; 2.山西天地煤机装备有限公司, 山西太原 030006)
引言
在煤矿橡胶密封元件中,O形橡胶密封圈以其结构简单、密封可靠、价格便宜、生产方便等优点,成为矿山机械生产数量最多、使用最广泛的一种密封元件[1],其密封性能很大程度上决定了产品的故障率。然而在实际调研中发现,O形圈在装配过程中极易扭曲和变形,甚至发生表面擦伤,这很可能造成设备密封失效,产生“跑、冒、滴、漏”的现象[2]。同时由于O形圈安装在产品内部,很难观察到安装后的情况。因此,通过对密封圈安装状态的模拟,可清晰直观地观察到O形圈到达安装位置后的情况,从而指导其结构设计。
O形圈的常用材料是橡胶,和金属材料不同的是,橡胶的力学行为呈现超弹性特点,具有明显的大变形及高度非线性的几何特征[3]。因此在对橡胶元件进行有限元模拟时,其大变形和非线性特征会导致节点出现扭曲,从而使得计算结果发散[4]。迄今为止,国内外学者创立了很多理论模型来表征橡胶的力学特征,但是由于橡胶材料本构关系的特殊性,许多设计工程师倾向于通过线性模型简化橡胶材料的建模,因此橡胶的非线性效应要么是未知的,要么是被忽略的。所以橡胶材料的本构关系研究成为行业的难点和热点问题。随着计算机以及有限元分析技术的蓬勃发展,能够利用计算机来研究超弹性材料的结构优化和工程应用,许多不同的应变能函数已在商业有限元软件中实现,例如Mooney-Rivlin,Ogden和Yeoh方程[5-8]。
目前有关O形圈的研究有很多,具体涉及到了很多领域[9]。杜晓琼等[10]建立了3种不同密封模型,对比分析了油压和压缩率对密封性能的影响规律。王刚等[11]建立了O形圈有限元模型,分析了载荷和压缩率对应力分布的影响。康家明等[12]对比研究了燕尾沟槽和矩形沟槽对密封圈密封性能的影响。王朝晖等[13]通过理论计算得出Mooney-Rivlin模型的材料参数。王财生等[14]考虑了O形圈在径向和轴向受限的力学行为研究。综上,这些研究大多集中在工作状态下O形圈的力学分析,对于O形圈安装过程的研究并不多见,另外对于橡胶材料参数的获取大多来源于理论计算,缺乏实验探究。
本研究基于有限元法和实验法确定Mooney-Rivlin模型来表征橡胶材料的力学特性,并获得了材料参数;建立了考虑安装状态的O形圈有限元模型,对某型液压缸用O形圈的力学行为展开仿真分析;研究了不同摩擦系数、初始压缩率和安装圆角对最大Von Mises应力、接触应力和剪切应力的影响,为O形橡胶密封圈的结构优化设计和失效分析提供理论依据。
1 橡胶材料本构模型及力学实验
1.1 本构模型
橡胶是一种多重非线性材料,包括材料非线性、几何非线性和边界非线性[15],这使得对橡胶的分析研究比较困难。在有限元分析中,采用本构理论来描述橡胶材料的超弹性行为。ANSYS包含了丰富的本构模型,主要包括Mooney-Rivlin,Yeoh,Ogden模型等。其中使用最广泛的是Mooney-Rivlin模型,可以模拟大多数橡胶材料的力学特性[16]。Mooney-Rivlin模型常用的有2,3,5,9参数共4种方程,参数越多,拟合的精度越高。本研究选用的是5参数Mooney-Rivlin模型,其应变能密度函数如下:
W=C10(I1-3)+C01(I2-3)+C20(I1-3)2+
(1)
(2)
(3)
(4)
式中,W是应变势能;C10,C20,C11,C01,C02和D1是与温度相关的材料参数;I1和I2是Cauchy-Green应变的不变量;J是由变形引起的体积变化的度量,由于橡胶是不可压缩材料,所以J=1;λ1,λ2和λ3是主伸张率,下标1,2和3表示3个相互正交的方向。W的具体形式由实验方法确定[17]。
1.2 力学实验
单轴实验作为探究橡胶材料力学性能的基础实验,由于实验方法简单,便于操作,制样方便,而且比较容易得到可靠的实验数据,从而被广泛应用在实验室中来获取橡胶材料的应力-应变曲线。橡胶材料的应力-应变曲线具有非线性特点,其力学行为与众多因素密切相关,包括实验环境、工况条件、加载速率等[18]。本研究实验用橡胶是天然橡胶,硬度值为71 HA。如图1所示,橡胶试样参照国标GB/T 528—2009制成Ⅰ形哑铃状试样,试样厚度为(2.0±0.2) mm,试验段长度为(25.0±0.5)mm,同一种胶料制备3个哑铃试样,实验结果取平均值。实验设备是电子万能实验机,将所制备的哑铃试件安装在电子万能实验机上,以(500±50)mm/min的恒定速率开始拉伸,直至试样破坏为止,记录下载荷-位移曲线。如图2所示,将记录的载荷-位移曲线转换为应力-应变曲线,其中σ表示拉伸应力,ε表示拉伸应变,可以看出橡胶材料的应力-应变曲线表现出典型的非线性特性。在较小的载荷作用下就能产生明显变形,拉伸长度可以比原来的长度延长几倍。

图1 橡胶试样Fig.1 Specimens of rubber

图2 橡胶材料应力-应变曲线Fig.2 Stress-strain curve of rubber material
2 O形圈非线性有限元分析
2.1 几何模型
液压缸是液压系统最常用的元件之一,其密封效果直接决定着液压系统的传动效率,而O形圈以其结构简单,拆装方便等优点,成为液压缸中使用最广泛的密封形式之一[9]。如图3所示,本研究以某型液压缸内O形圈为例建立几何模型,模型处于安装状态,主要由缸体、活塞杆和O形圈3部分组成。根据几何模型的受力特点,可将O形圈简化成二维轴对称模型,对称轴为y轴,从而将三维问题简化为二维问题[10]。密封槽尺寸按照国标GB/T 3452.3—2005选取,具体见表1。
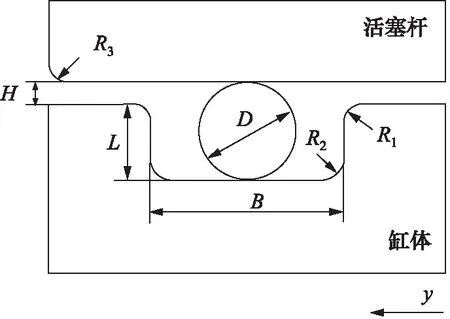
图3 密封结构的几何模型Fig.3 Geometric model of sealing structure
2.2 材料参数
在有限元计算中,准确的材料参数对有限元结果是十分重要的。如果没有准确的橡胶材料参数,就很可能出现计算结果不收敛、计算结果误差大以及计算成本过高等问题。本研究对缸体与活塞杆材料均采用结构钢,密度7850 kg/m3,弹性模量208 GPa,泊松比0.3。O形圈是橡胶材料,将单轴拉伸实验得到的材料数据,输入到ANSYS软件中生成应力-应变曲线,如图4所示,通过实验曲线和有限元拟合曲线对比,发现5参数Mooney-Rivlin模型拟合曲线和实验曲线几乎吻合,所以选择5参数Mooney-Rivlin模型来表征天然橡胶的力学行为。表2是橡胶超弹性材料常数。

表1 几何模型部分尺寸Tab.1 Some dimensions of geometric model mm
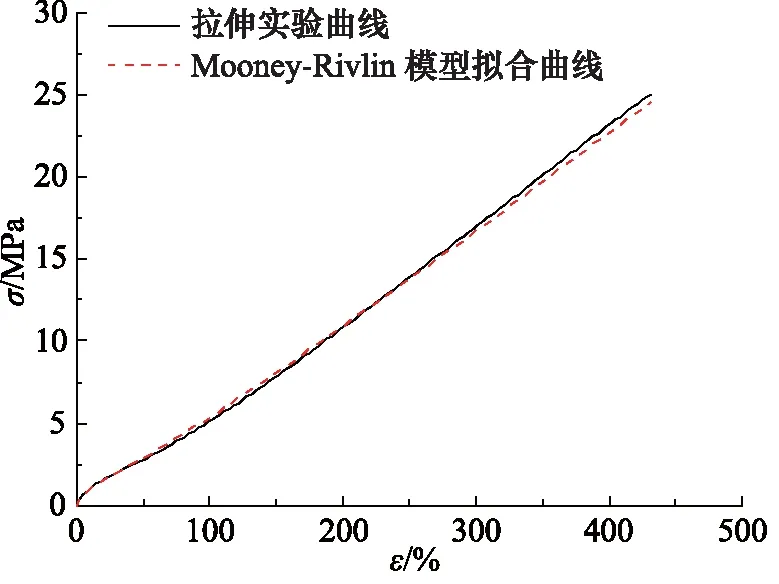
图4 实验曲线与Mooney-Rivlin模型拟合曲线Fig.4 Experimental curve and Mooney-Rivlin model fitting curve
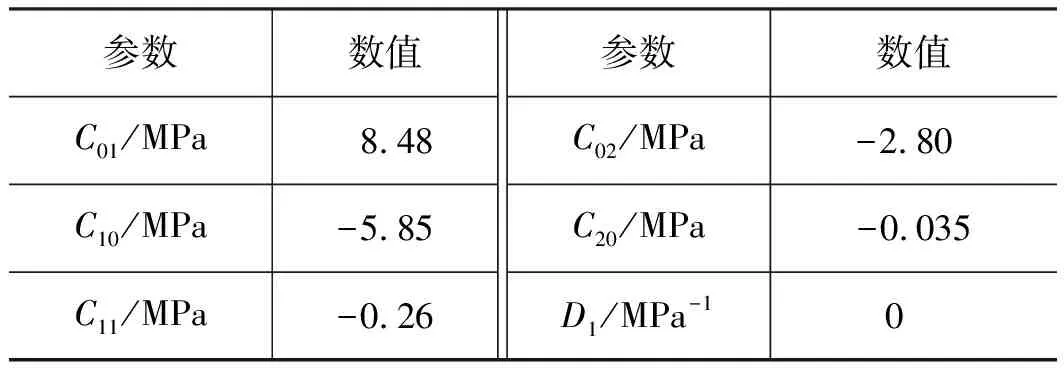
表2 橡胶超弹性材料参数Tab.2 Hyperelastic material parameters of rubber
2.3 网格划分及边界条件
图5给出了有限元模型的网格划分,合计4825节点,1508个单元。当网格在此基础上增加到2倍,其计算结果误差为0.5%以内,但计算时间却增加数倍。因此,本案例分析使用的网格合理,能得到满意的计算精度。

图5 网格划分Fig.5 Meshing
通过分析O形圈的安装状态,给定模型的初始压缩率为10%。O形圈与缸体内侧、O形圈与沟槽内壁接触,接触类型设置为摩擦接触,摩擦系数设置为0.15。考虑到O形圈装配是一个先拉伸后压缩的过程,给缸体设置固定约束,给活塞杆在y方向施加5 mm 的位移量。
2.4 结果分析
图6给出密封模型安装过程中的应力变化曲线,可以看出安装过程中Von Mises应力和剪切应力的变化趋势一样,都是先陡增至峰值,然后缓慢减小至平稳状态。这说明了密封模型在安装过程中发生了畸变,即存在一个最大安装应力。在安装过程中,O形圈在活塞杆轴向作用下与沟槽侧壁接触,此时最大安装应力出现在O形圈与活塞杆安装圆角接触的地方。当越过安装圆角后,应力值逐渐减小,而当活塞杆完全进入后,应力值趋于稳定。图7给出O形圈在安装过程中的应力变化曲线,可以看出O形圈在安装过程中Von Mises应力和剪切应力的变化趋势一样,都是应力值陡增至平稳状态。即在活塞杆轴向作用下,O形圈应力值一直增大,直至活塞杆完全进入时应力值趋于稳定。因此在实际应用中应选择合适的参数来保证O形圈的密封性能。
3 不同因素对O形圈安装状态的影响分析
3.1 摩擦系数的影响
在实际装配过程中,接触面的摩擦是O形圈损坏的主要原因,因此必须探讨接触面摩擦系数f对O形圈安装状态的影响规律。图8给定不同摩擦系数值0.05,0.10,0.15,0.20,0.25,0.30,0.35,0.40,初始压缩率10%,安装圆角半径为0.5 mm时,O形圈安装过程中的最大Von Mises应力、最大接触应力和最大剪切应力曲线。可以看出,应力值随着摩擦系数的增大而增大,在摩擦系数0.25时应力值有一定的突变,因此要严格控制接触面的摩擦系数,避免应力集中,以延长O形圈的使用寿命。
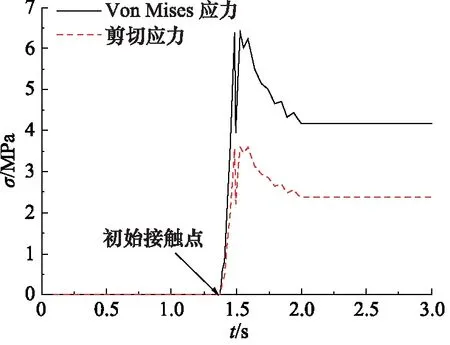
图6 安装过程中模型应力变化曲线Fig.6 Model stress curves during installation

图7 安装过程中O形圈应力变化曲线Fig.7 O-ring stress curves during installation
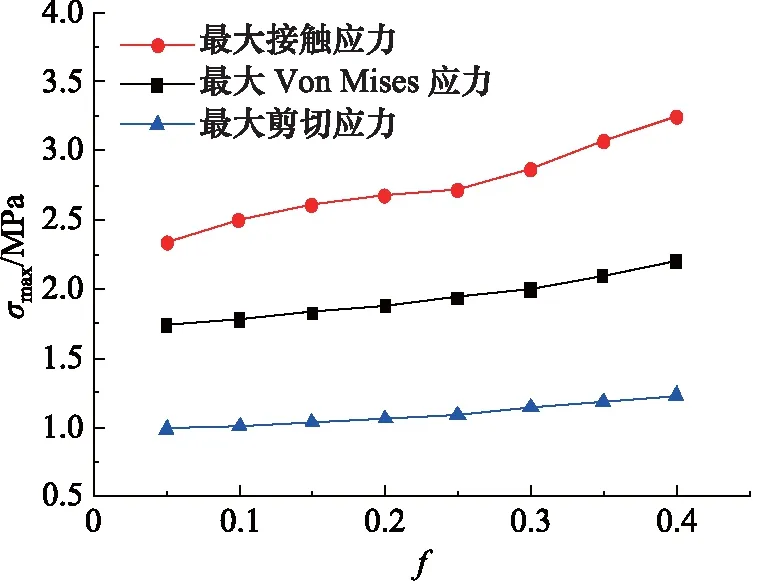
图8 安装过程中O形圈最大应力随不同摩擦系数的变化曲线Fig.8 O-ring maximum stress curves at different friction coefficients during installation
3.2 初始压缩率的影响
O形圈的安装由于加工误差等原因,会形成一个初始的径向间隙H。H对O形圈的密封性能产生着重要影响。定义初始压缩率,其公式如下:
(5)
式中,D为O形圈在自由状态下的截面直径;H为初始的径向间隙。
图9给定不同初始压缩率δ为5%,10%,11%,13%,15%,17%,19%,摩擦系数0.05,安装圆角半径为0.5 mm时,O形圈安装过程中最大Von Mises应力、最大接触应力和最大剪切应力曲线。可以看出,应力值随着初始压缩率的增大而增大,尤其是在初始压缩率大于10%以后应力值显著增大。在初始压缩率大于15%后,最大接触应力与最大Von Mises之间的差距逐渐缩小,也就是说O形圈的密封性能变好,但损伤的可能性增加。因此,合理的设计初始压缩率,可以较好的控制O形圈的应力集中。
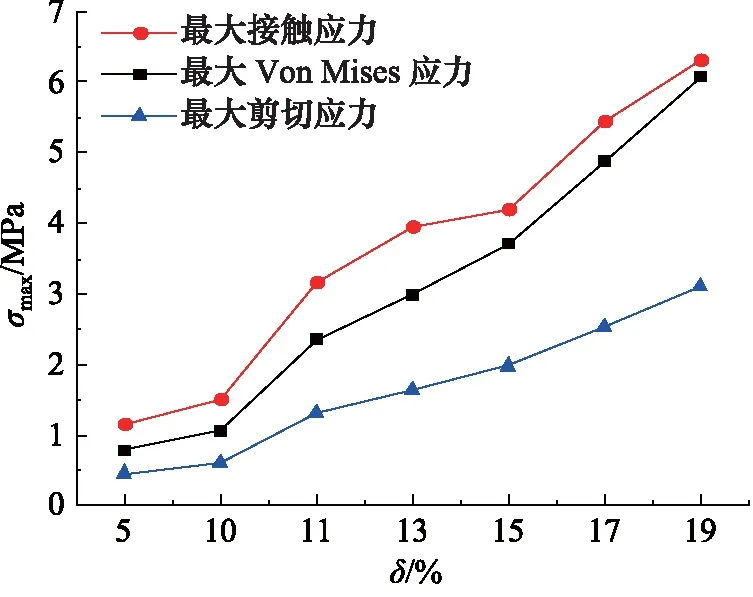
图9 安装过程中O形圈最大应力随不同初始压缩率的变化曲线Fig.9 O-ring maximum stress curves at different compression ratios during installation
3.3 安装圆角的影响
由于O形圈在安装过程中容易发生划伤、扭转、过量拉伸等损坏,从而影响密封性能,因此在O形圈安装端部引入安装圆角半径R3,以防O形圈被损伤。图10给定不同安装圆角半径为0.2,0.5,0.8,1.0,1.2,1.5,2.0 mm,摩擦系数为0.05,初始压缩率为10%时,O形圈安装过程中最大Von Mises应力、最大接触应力和最大剪切应力曲线。可以看出,随着安装圆角的增大,各最大应力变化很小,基本呈水平趋势。因此,安装圆角的大小对安装时O形圈的影响不大。
4 结论
(1) 基于单轴拉伸实验得到天然橡胶材料的应力-应变曲线,通过与有限元拟合曲线对比发现Mooney-Rivlin模型适合描述天然橡胶的材料特性;

图10 安装过程中O形圈最大应力随不同安装圆角的变化曲线Fig.10 Maximum stress curves of O-ring at different installing fillets during installation
(2) 建立了考虑安装状态的O形圈有限元模型,分析安装过程中的应力变化,结果表明,O形圈的应力逐渐陡增至平稳状态;
(3) 分析了不同摩擦系数f、初始压缩率δ和安装圆角半径R3对O形圈安装过程中最大Von Mises应力、最大接触应力和最大剪切应力的影响规律,发现应力值随着摩擦系数的增大而增大,当摩擦系数小于0.25时O形圈安装状态较好;随着初始压缩率的增大,应力值逐渐增大,当初始压缩率位于10%至15%之间时O形圈综合性能更好;而安装圆角的大小对O形圈的影响不大。

