一种气压自适应伺服活门的结构和特性

孙景凯， 王顺吉， 高 帅， 吴彦旭

(中国航发西安动力控制科技有限公司设计研究所， 陕西西安 710077)

引言

定压伺服活门是液压机械控制系统基础控制元件之一，自身是一个完整的闭环系统，可以为液压控制系统提供一个稳定的压力标准[1]。常见的定压伺服活门结构原理图见图1，其本质是一个进出口均可变化的分压器，当负载和进口压力变化时，定压伺服活门通过调节进口节流孔的大小来保证定压油压力稳定[2]。

在稳态下，根据力平衡关系，伺服压力p的大小主要由活门上端面所受合力F决定:

pS=F0+Kx+p0S

(1)

式中，S—— 活门阀芯面积

F0—— 弹簧装配预紧力

K—— 弹簧刚度

x—— 活门位移

p0—— 低压腔压力

王华威等[2]通过对定压活门主要结构参数的影响分析，提出了提高定压伺服活门稳定性的措施和设计方法，为获取高稳定性定压伺服活门指明了方向。在航空发动机机械液压控制系统中，常常采用环境敏感元件(气压、温度等)进行环境参数的采集，并将敏感元件的位移输出或者力值输出经过放大后作为控制变量，用于发动机的调节。基于此，考虑将定压伺服活门的伺服压力p作为变量用于伺服控制，在活门基本结构确定的情况下，改变弹簧装配预紧力F0、弹簧刚度K和低压腔压力p0是改变合力F实现伺服控制的技术实现途径。其中，低压腔压力p0作为液压系统基准压力之，一般为定值，不作为变量。宋佳彬[3]为解决汽车发动机配气机构气门飞脱、反跳问题，设计了刚度可变的截锥弹簧，实现了气门受力与转速相适应，这为通过设计变刚度弹簧实现伺服控制提出了借鉴。但在通过改变弹簧装配预紧力F0来实现伺服压力受控变化的尝试却很少，有必要进行进一步的研究。AMESim作为目前比较先进的航空发动机燃油控制系统仿真分析工具，对液压系统设计、系统性能分析、改进与提升、故障排查等发挥着越来越重要的作用[4-9]。

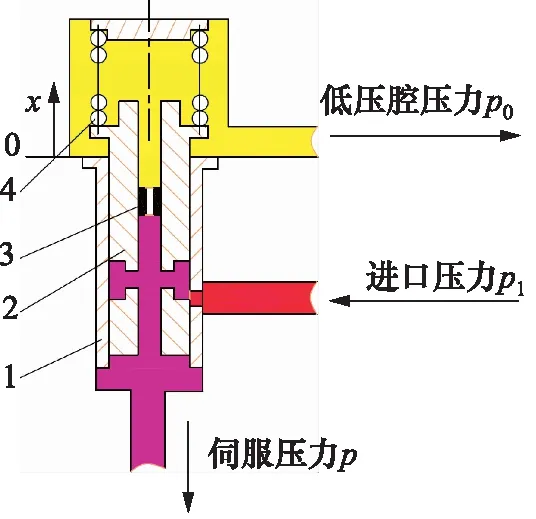
1.衬套 2.活门 3.节流嘴 4.弹簧图1 定压伺服活门结构原理图Fig.1 Schematic diagram of fixed-pressure servo valve

本研究按照由环境敏感元件感受环境条件变化从而改变定压伺服活门F0的思路出发进行研究，提出了一种气压自适应伺服活门结构，利用AMESim对提出的气压自适应伺服活门结构进行建模仿真，对影响伺服控制特性的关键影响因素进行深入的研究，为其工程应用和优化设计提供参考。

1 结构原理分析

在航空发动机控制计划中，通常选用发动机进口空气压力pt1和温度Tt1表征发动机外部条件的变化[10]，并使用pt1，Tt1作为控制变量对发动机进行稳态调节，比如发动机的慢车推力控制计划N=f(pt1)[11]、慢车高压转子转速控制计划nH=f(Tt1)和落压比调节规律ΠT=f(Tt1)[12]。

膜盒是常用的机械式气压/温度敏感元件，其中真空膜盒可以感受外部的绝对压力，闭口填充膜盒(膜盒内填充气体、液体或饱和蒸汽)可以感受外部环境温度，二者均可以感受外界环境变化输出位移或者输出力[13]，具有良好的测量精度和稳定性。

基于以上分析，提出一种基于机械式膜盒的气压自适应伺服活门，其结构原理图见图2，在图1定压伺服活门的基础上增加了膜盒组5和杠杆6，膜盒组与活门之间通过杠杆铰链相连，杠杆以O为支点，膜盒输出力的变化传递活门上，支点位置不同可以获得不同的杠杆比。

1.衬套 2.活门 3.节流嘴 4.弹簧 5.膜盒组 6.杠杆图2 气压自适应伺服活门结构原理图Fig.2 Schematic diagram of theair pressure adaptive servo valve

以感受外界大气压变化的真空膜盒组为例，分析其工作原理如下：

设定真空膜盒组在标准大气压下不向外输出力，此时该结构与定压伺服活门相同，向外输出恒定的伺服压力。当外界大气压发生变化时，真空膜盒组开始向外输出力值，通过杠杆将力传递到活门上，活门的受力平衡被打破，并发生运动，引起由衬套节流孔和活门工作边组成的进油口P通流面积发生变化，当活门到达新的受力平衡位置时，根据分压器原理，伺服压力便发生了变化，由此实现伺服压力随气压的自适应调节。

膜盒组输出力特性由膜片所受压力大小和有效面积决定，膜盒和膜盒组的输出力与单个膜片的输出力相同[14]，单个膜片的输出力fm为：

fm=(pH0-pH)Se

(2)

式中,pH0—— 膜盒输出力为0 N的基准大气压力

Se—— 膜片有效面积

膜盒结构确定后为固定值。工程实际中，为了获取真空膜盒的有效面积，一般通过以下试验方法进行数据获取：在密闭容腔内，在基准大气压下，保持真空膜盒组自由高度固定不变，此时膜盒组输出力值为0 N，通过抽真空装置改变容腔气压，给定容腔不同的气压值pH，测量对应的真空膜盒输出力值fm，fm随pH变化特性线的斜率即为真空膜盒的有效面积。

用作输出力的膜盒，随气压变化总要发生位移，膜片的位移会影响有效面积，进而影响输出力。为了减小位移的影响，一般采用膜盒组的方式把膜片的输出位移控制在较小的范围内。采用膜盒组后，在总位移Ls一定的情况下，单个膜片的位移就减小为Ls/(2z)，z为膜盒个数，从而降低了对输出力的影响[14]。

从式(2)看出，膜盒输出力fm与大气压力pH成线性比例关系，这对应用于伺服控制是非常有利的，可以降低系统阶次，简化系统结构。

2 数学模型

根据气压自适应伺服活门的结构和工作原理，以活门为研究对象，对其进行受力分析。活门主要受液压力、弹簧力、膜盒杠杆力、液动力和阻尼力作用。在稳态下，活门的受力平衡方程为：

pS+Fs=F0+Kx+p0S-fm/λ

(3)

式中，Fs—— 稳态液动力，Fs=KsAΔp

Ks—— 稳态液动力系数

A—— 活门进口开度面积

Δp—— 活门进口前后压差

将式(2)代入式(3)可得：

pS+Fs=F0+Kx+p0S-Se(pH0-pH)/λ

(4)

因此，伺服压力p变成了与活门运动位移x和大气压力pH的函数关系：

=αx+βpH+γ

(5)

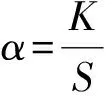
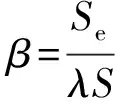
γ—— 表征了结构的初始设定条件

在稳态下，由进油口进入活门的流量与从节流嘴流出的流量满足流量平衡关系，其稳态流量平衡方程为：

(6)

式中，Cp1—— 进油口流量系数

Ap1—— 进油口通流面积，由衬套与活门相对位置构决定，受活门受力平衡位置控制

C3—— 节流嘴的流量系数

A3—— 节流嘴的流通面积

ρ—— 油液的密度

在某一平衡位置，当大气压力pH发生变化时，活门在弹簧力、膜盒杠杆力、伺服腔压力、低压腔压力、液动力、阻尼力的共同作用下发生运动，活门的动力学方程为：

(7)

Kt—— 瞬态液动力系数

C—— 活门运动时的阻尼系数

在动态变化过程中，伺服腔满足如下流量平衡关系：

(8)

式(4)、式(6)～式(8)描述了气压自适应伺服活门的动静态特性。

3 仿真分析

3.1 仿真模型的建立

为研究气压自适应伺服活门的工作特性，根据其工作原理和结构参数，建立了气压自适应伺服活门的AMESim模型[15-17]，如图3所示。

图3 气压自适应伺服活门AMESim模型Fig.3 AMESim model of air pressure adaptive servo valve

模型中真空膜盒组使用函数运算表示，其有效面积使用某型真空膜盒组(4组膜盒)实测数据。通过把大气压力pH作为输入量，模拟pH变化的过程。设置仿真时间为10 s，采样间隔为0.01 s，仿真参数见表1。

表1 模型参数Tab.1 Model parameters

3.2 仿真结果

设置大气压力pH，分别按照斜坡输入和阶跃输入两种方式来模拟大气压力的连续变化和突变过程，仿真结果见图4～图7。

图4为pH按照斜坡输入从0.101 MPa减小至0.026 MPa再增至0.101 MPa的过程，模拟大气压力从海平面到10 km高空再到海平面，伺服压力p随时间的变化过程。图5为变化过程中伺服压力随大气压力pH的特性关系，pH从0.101 MPa 变化至0.026 MPa时，伺服压力p从1.05 MPa变化到0.63 MPa，伺服压力p与pH保持了良好的线性关系。

图4 大气压力和伺服压力随时间变化曲线Fig.4 Changing curve of atmospheric pressure and servo pressure with time

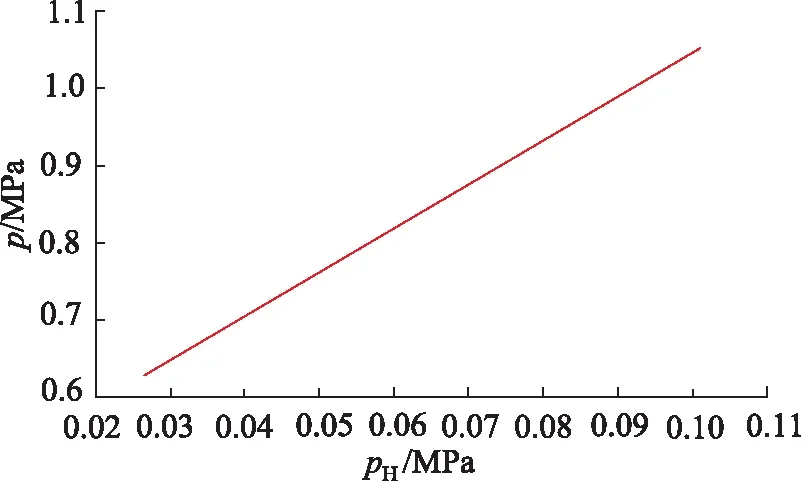
图5 伺服压力随大气压力变化曲线Fig.5 Changing curve of servo pressure with air pressure

图6a为pH按照阶跃输入从0.101 MPa逐步突变至0.075，0.054,0.026 MPa的过程，模拟大气压力从海平面逐步突变到2，5，10 km的变化过程中伺服压力p的变化情况；图6b显示了大气压力从0.101 MPa突降到0.075 MPa时伺服压力p与大气压力pH动态变化过程，可以看出，从大气压力开始变化到伺服压力稳定的时间为0.002 s(此处仿真采样时间为0.001 s)，伺服压力表现出了良好的跟随性和响应速度。

图7显示在大气压力pH变化过程中，活门位移x随时间的变化过程，可以看出，在0～10 km高度气压变化范围中，活门位移最大变化量为0.0194 mm(0 km时x=1.9410 mm；10 km时x=1.9604 mm)，变化量值较小，根据杠杆原理，通过杠杆反馈到真空膜盒组的位移为0.0138 mm，平均到每一片膜片的位移为0.0017 mm，对于膜盒来说，位移变化对输出力的影响可以忽略不计。

图6 伺服压力随大气压力变化曲线Fig.6 Changing curve of servo pressure with air pressure step

图7 活门位移随大气压力变化曲线Fig.7 Changing curve of spool displacement with air pressure step

上述结果表明，基于改变环境敏感元件、改变定压伺服活门F0的思路提出的气压自适应伺服活门具备良好的伺服控制特性和可实现性。

4 关键结构参数影响分析及选取

文献[2]已完成了影响定压伺服活门特性的阀芯面积S、阻尼系数C、出口流通面积A等的定量分析，其结果也适用于气压自适应伺服活门。这里主要对气压自适应伺服活门设计中的关键结构参数影响进行分析。

4.1 弹簧刚度

弹簧在使用过程中会存在衰减情况，为模拟弹簧衰减对伺服特性的影响，分别在弹簧刚度K为5.0，4.5，4.0 N/mm情况下进行仿真，其结果见图8。

图8 弹簧刚度的影响Fig.8 Influence of spring stiffness

从图8可以看出，弹簧刚度会影响伺服压力p的大小，但不改变伺服压力p的线性，K值越大，p也越大。因此应用过程中需考虑弹簧衰减对伺服压力p的影响，当性能衰减影响伺服控制时应采取措施进行衰减补偿。

4.2 杠杆比

杠杆比λ是气压自适应伺服活门设计的基本参数，也是性能调整的主要手段之一，分别在杠杆比λ为0.8，1.0，1.2，1.4，1.6的情况进行试验，大气压力变化范围0～0.101 MPa，其仿真结果见图9。

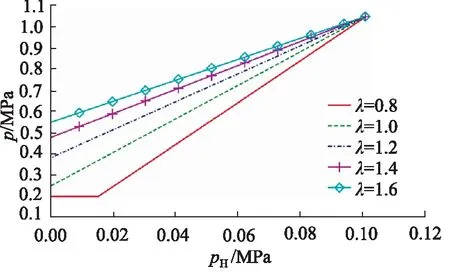
图9 杠杆比的影响Fig.9 Influence of lever ratio

从图9可以看出，杠杆比λ主要影响伺服压力p的斜率，改变了伺服压力的变化范围，杠杆比越小，斜率越大，伺服压力调节范围越大。同时杠杆比也会影响伺服活门的可工作大气压力范围。在合适的杠杆比范围内，伺服压力能随大气压力pH在0～0.101 MPa之间线性变化，当杠杆比小于某一值时，会出现伺服压力不再随大气压力变化，并保持与低压腔压力相等的情况。出现该现象的原因是：p1进口油压的初始预开量设定为2 mm，随着大气压力pH的减小，活门逐步运动并关小p1进口油压的通流面积，如图10所示，当杠杆比为0.8、大气压力为0.015 MPa时，活门运动位移达到了2 mm，关闭了进口油压通流面积。此时，伺服活门的可工作气压范围变为了0.015～0.101 MPa。

图10 杠杆比对活门位移的影响Fig.10 Influence of lever ratio on spool displacement

气压自适应伺服活门工作范围缩小的特性，刚好可以为伺服控制上的阀值截止特性所应用，例如某性能要求在10 km以下高度随大气压力进行伺服控制，10 km以上高空为恒值控制，就可以通过选择合适的杠杆比，将10 km以上的伺服性能进行屏蔽。因此，在设计时，需要根据伺服控制特性需求、大气压力工作范围、活门运动行程等合理选择杠杆比。

4.3 膜盒有效面积

膜盒有效面积Se是气压自适应特性实现的基本参数，分别选取有效面积Se为20，50，80，100 mm2进行试验，大气压力变化范围0～0.101 MPa，其仿真结果见图11。

由图11可以看出，膜盒有效面积Se同样影响伺服压力曲线的斜率，主要改变伺服压力的初始设定值，膜盒有效面积越大，伺服压力初始设定值越大。在伺服活门结构不变的情况，膜盒有效面积Se的大小决定了在标准大气压下的伺服压力基准设定值。有效面积增加时，伺服压力会出现大于设定压力的情况，当面积减小时，会出现伺服压力小于设定压力的情况。另一方面，当有效面积减小到一定程度时，特性曲线的斜率便趋于平缓，伺服压力变化过小，不利于进行伺服控制。

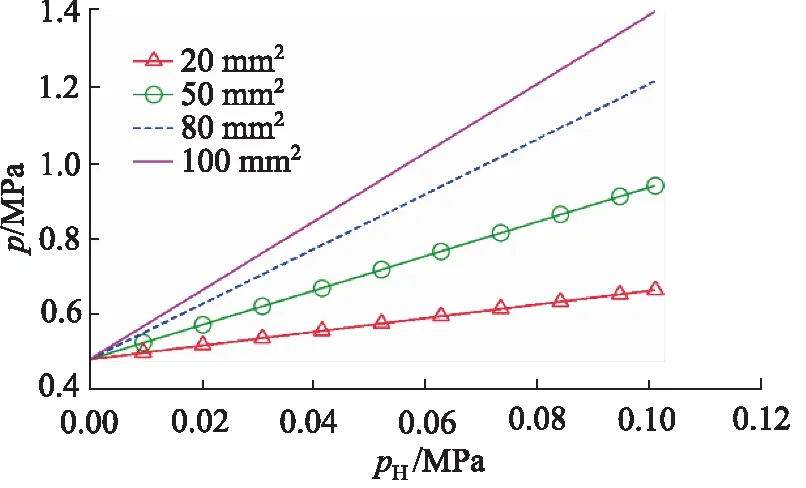
图11 膜盒有效面积的影响Fig.11 Influence of effective area of altitude capsule

在上述情况下，虽然气压自适应伺服活门还具备自适应功能，但是与设定要求已发生偏离。产生偏离的主要原因是膜盒有效面积Se的变化引起式(5)中γ≠γ0(γ0为活门初始设定值)，当γ>γ0时，伺服压力偏大；当γ<γ0时，伺服压力偏小。这两种状态在标准大气压下，膜盒均向外输出力，膜盒始终处于受力状态，会影响膜盒的工作寿命。

因此当活门结构和伺服压力设定值确定时，通过使γ=γ0进行膜盒有效面积Se选取；当膜盒已选定(有效面积Se已确定)时，通过匹配活门参数、弹簧参数等进行匹配设计。一般地，为获得理想的气压自适应控制特性并延长膜盒寿命，应确保膜盒在工作气压范围内的最大输出力小于弹簧初始预压力，同时应尽量确保膜盒在标准大气压下的输出力为0。

4.4 其他影响因素

除上述结构参数外，元件自身的特性也会对伺服特性产生影响，比如真空膜盒组的滞环特性、杠杆铰链机构的装配间隙引起的滞环特性等。

滞环特性是薄膜、膜盒类压力敏感元件的的固有特性，限制薄膜/膜片的最大位移可以大大减小滞环，如第1节所述，采用膜盒组的形式可以减小单个膜片的位移，也可以减小真空膜盒组的滞环。

杠杆机构的间隙在实际工程中不可避免，也会对伺服压力特性带入滞环。该滞环的引入主要原因是杠杆受力方向变向和空行程。在气压自适应伺服活门结构设计中，最有效的消除或者减小滞环的措施就是避免出现杠杆受力为0的状态，也就是在整个工况范围内保证杠杆始终受力，比如在设置弹簧初装预紧力F0时，保证预紧力F0大于整个工况范围内的杠杆力。

5 应用实例

将气压自适应伺服活门结构应用于某型活塞位置控制系统中，如图12所示。用滑阀代表活塞，活塞左腔通伺服压力p驱动活塞运动，右腔通低压腔压力p0，活塞通过弹簧力进行位置反馈，形成闭环系统。

图12 活塞位置控制模型Fig.12 Piston position control model

设置活塞无杆腔直径为40 mm，有杆腔直径15 mm，弹簧刚度40 N/mm，活塞运动行程x1为25 mm。模拟大气压力从0.101～0.026 MPa之间线性变化进行试验，活塞位置随大气压力pH变化的仿真结果如图13所示。

图13 活塞位移随大气压力变化曲线Fig.13 Changing curve of piston displacement with air pressure

从图13可以看出，随着大气压力的减小，活塞位移按照线性关系从20.64 mm逐渐减小(向左运动)，当大气压力pH为0.026 MPa时，活塞位移为7.72 mm，这个过程中活塞总运动行程为12.92 mm，表现了良好的控制特性。当在伺服油路和上低压油路增加节流油嘴等节流元件后，即可实现对活塞运动速度的控制和调节，如图14所示，节流油嘴流量越大，活塞运动速度越快。

图14 节流油嘴流量对活塞运动的影响Fig.14 Influence of metering orifice on piston motion

活塞位置的控制是自适应伺服控制的基本应用场景之一，当活塞位置与其他控制特性相关联时，便能实现不同控制特性，例如将活塞位置与燃油计量特性相关联时，便能实现计量燃油随大气压力自适应伺服控制。

6 结论

本研究介绍了一种用机械液压式气压自适应伺服活门，通过理论分析和仿真分析，得出了伺服压力p随大气压力pH气压自适应伺服特性，并对其关键影响因素的分析研究和应用实例分析，得出以下结论：

(1) 基于真空膜盒改变伺服活门预紧力构建气压自适应伺服活门的方法具有可行性，可以实现伺服压力随气压的自适应调节，可用于伺服控制，在航空发动机控制上具有良好的应用前景；

(2) 杠杆比λ和膜盒有效面积Se是关键设计参数，均会改变伺服压力曲线的斜率，但是影响不同，杠杆比主要影响伺服压力变化范围，杠杆比越小，伺服压力变化范围越大；膜盒有效面积主要影响伺服压力的初始设定值，膜盒有效面积越大，初始设定值越大，参数的选择应确保膜盒在工作气压范围内的最大输出力小于弹簧初始预压力，同时尽量保证膜盒在标准大气压下的输出力为0；

(3) 杠杆比λ会影响伺服活门的工作气压范围，利用该特性合理匹配伺服活门运动行程，可获得不同的阀值伺服特性。