基于伯格斯模型的岩石非线性蠕变损伤模型研究

李忠君 盛冬发 张容国

（西南林业大学土木工程学院，云南 昆明 650224）

0 引言

岩石蠕变特征是指岩石在外部因素影响下其应变随时间变化的过程，它是岩石流变力学的重要组成部分。大量岩石工程表明，蠕变特征是影响岩石工程长期稳定性和安全性的主要因素，建立表征岩石蠕变全过程的蠕变模型一直是研究的热点和难点［1］。传统蠕变模型由理论线性元件组合而成，例如伯格斯模型、西原模型等蠕变模型能很好地表征岩石瞬时变形、减速和等速蠕变阶段。而岩石蠕变是典型非线性问题，传统蠕变模型难以描述岩石非线性蠕变特征。因此，为保证岩石工程在服役期间的安全性，岩石非线性蠕变模型研究显得尤为重要。

岩石在蠕变过程中，其内部微孔洞和微裂隙不断发展和贯通，岩石有效承载面积逐渐减小，最终使得岩石失稳破坏，该现象主要受岩石损伤影响，发生在岩石加速蠕变变形过程［2］。近年来，一些学者通过损伤理论和提出新的非线性体表征岩石非线性蠕变特征。如宋勇军等［3］将分数阶微积分软体元件、幂函数黏塑性体和弹性元件串联，得到能够描述岩石蠕变全过程的非线性黏弹塑性流变模型。张亮亮等［4］基于Kachanov 损伤理论建立了损伤变量与时间的函数关系，将其引入黏弹塑性体，得到了非线性损伤蠕变模型，采用Levenberg-Marquardt 算法对该模型进行参数辨识，并基于三维压缩蠕变试验数据验证了该模型的合理性和可行性。部分学者提出的非线性蠕变模型还不能较好地描述岩石非线性蠕变特征，模型参数较多且不易辨识。鉴于此，本研究在伯格斯模型基础上串联一个黏塑性损伤体，得到了非线性蠕变损伤模型，该模型参数较少且易辨识，并结合相关文献压缩蠕变试验数据验证了模型的合理性和适用性。

1 岩石非线性蠕变损伤模型

1.1 蠕变损伤模型的建立

图1为伯格斯模型蠕变曲线。由图1可知，伯格斯模型是由弹性体、黏弹性体和黏性体组成的四元件组合模型。图1中，σ为应力，MPa；E1为弹性体的弹性模量，MPa；η1为黏性体的黏性系数，MPa ⋅h；E2、η2分别为黏弹性体的弹性模量和黏性系数，MPa、MPa·h；ε1、ε3、ε2分别为弹性体、黏弹性体、黏性体的应变。

图1 伯格斯模型蠕变曲线

由图1 可知，当岩石所受应力水平小于长期强度时，在加载瞬间将产生弹性变形，用弹性体予以描述。当瞬时弹性变形完成后，随着时间的增加，岩石将发生蠕变变形。在岩石蠕变变形过程中，蠕变率随时间增加而逐渐减小，并最后趋于一个定值ε̇= σ η1。该蠕变变形过程分为减速和等速蠕变阶段，可用黏弹性体和黏性体分别描述减速和等速蠕变阶段。而伯格斯模型由线性元件串并联组合而成，能较好地描述岩石瞬时弹性应变、减速和等速蠕变阶段，难以描述岩石加速蠕变特征。

当岩石所受应力水平大于长期强度时，岩石将很快进入加速蠕变阶段，蠕变曲线呈现明显非线性特征。岩石内部新生微缺陷不断发展并融合贯通，其力学性能不断劣化，该力学行为称作岩石损伤演化过程。利用损伤变量与时间呈现负指数函数关系描述岩石在加速蠕变阶段的损伤演化过程［5］，则损伤演化方程如式（1）。

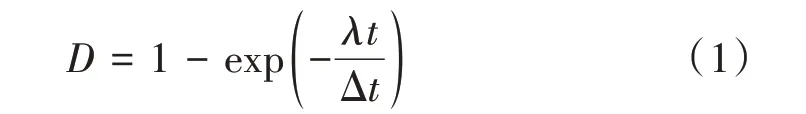
式中：D 为损伤变量，Δt 为单位时间，h；λ 为岩石损伤程度影响系数。当t →0 时，D = 0；当t → ∞时，D = 1，符合损伤演化规律。

将损伤变量引入黏性元件并与应力触发元件并联，得到黏塑性损伤体。根据Lemaitre 应变等效原理，则黏塑性损伤体的应变如式（2）。

式中：ε4和η3分为黏塑性损伤体的应变和黏性系数，MPa ⋅h；σs为长期强度，MPa。

岩石蠕变过程存在弹性、黏性、黏弹性和黏塑性等多种变形。因此，将黏塑性损伤体与伯格斯模型串联，得到非线性蠕变损伤模型，如图2 所示。该模型能较好地描述岩石蠕变全过程，弥补了伯格斯模型难以描述岩石加速蠕变的不足。图2 中，σ1、σ2、σ3、σ4分别为弹性体、黏性体、黏弹性体、黏塑性损伤体的应力，MPa。

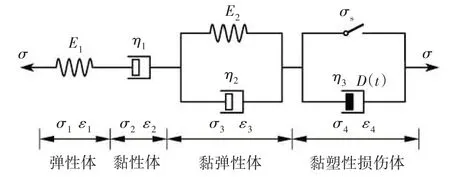
图2 非线性蠕变损伤模型

1.2 蠕变损伤模型的一维和三维蠕变方程

令总应力为σ，应变为ε，根据蠕变模型串并联性质，非线性蠕变损伤模型应力—应变关系如式（3）。

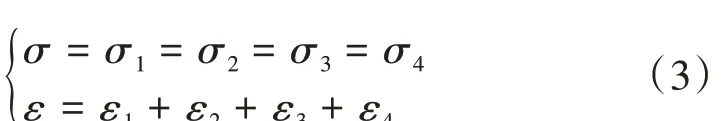
该模型各部分本构关系如式（4）。

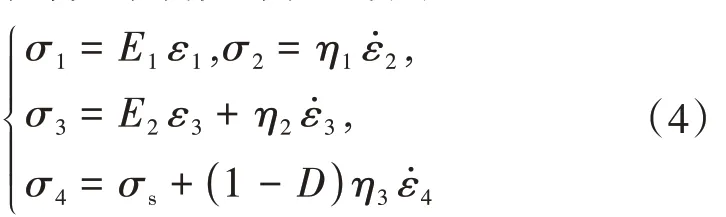
将式（4）代入式（3），根据叠加原理可得非线性蠕变损伤模型在一维应力状态下的本构方程和蠕变方程，有以下两种情况。

①当σ < σs时，非线性蠕变损伤模型退化为伯格斯模型，岩石出现瞬时弹性、黏弹性和黏性蠕变，其本构方程和蠕变方程分别为式（5）、式（6）。

②当σ ≥σs时，岩石出现瞬时弹性、黏弹性、黏性和黏塑性蠕变，非线性蠕变损伤模型的本构方程和蠕变方程分别为式（7）、式（8）。

在实际岩石变化过程中，岩石通常处于更复杂的三维应力状态，则一维应力状态下的蠕变方程将不再适用。建立岩石在三维应力状态下的蠕变方程更加符合实际工程。为建立合理的三维蠕变方程，假定岩石为各项同性材料，且在减速和等速蠕变阶段未产生新损伤，只有加速蠕变阶段才有新损伤出现。

岩石应力张量σij和应变张量εij分别由球应力张量 σmδij、偏应力张量 Sij和球应变张量 εmδij、偏应变张量eij组成，即式（9）。

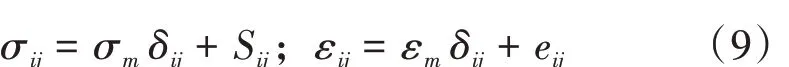
在三维应力作用下，根据叠加原理，非线性蠕变损伤模型的总应变张量εij( )t 如式（10）。

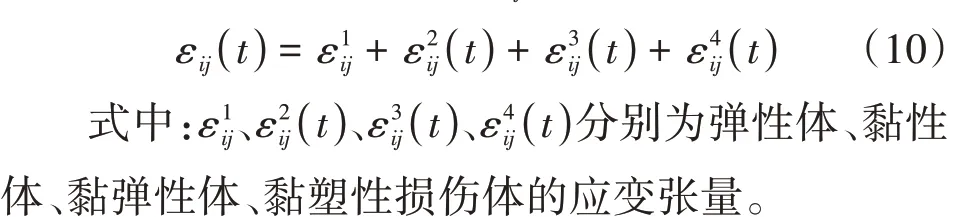
假定岩石在球应力张量作用下只有弹性的体积变形，而蠕变特征主要受偏应力张量控制。因此，弹性体的三维本构关系如式（11）。

式中：G1和K1分别为弹性体的剪切模量和体积模量，MPa、MPa。

黏性体的三维本构关系如式（12）。

式中：η1为黏性系数，MPa ⋅h。

黏弹性体的三维本构关系如式（13）。

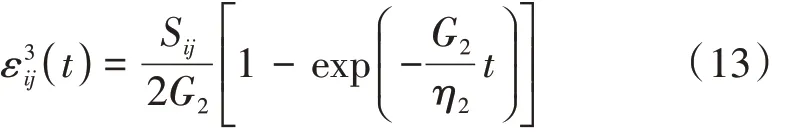
式中：G2、η2分别为黏弹性体的剪切模量和黏性系数，MPa、MPa·h。

根据Perzyna黏塑性理论［6］，黏塑性损伤体的三维本构关系如式（14）。

函数，n 为幂指数，通常取为1；F 为岩石屈服函数；F0为岩石屈服函数初始值，为了便于计算通常取1；Q 为塑性势能函数；η3为黏塑性损伤体的黏性系数，MPa·h。

由于岩石蠕变特征主要受偏应力张量控制，受球应力张量影响较小，故屈服函数F如式（15）。

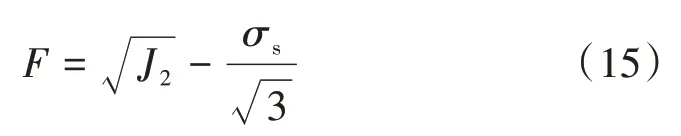
式中：J2为偏应力张量第二不变量，MPa，即

对常规三维压缩蠕变试验有 σ1> σ2= σ3，其中σ1为轴压，σ2和σ3为围压，则有式（16）。

联立式（9）至式（16），结合叠加原理，三维应力状态下非线性蠕变损伤模型的蠕变方程如式（17）、式（18）。

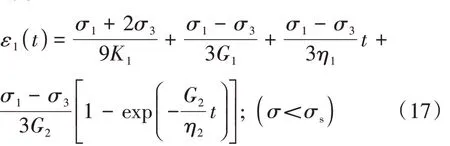
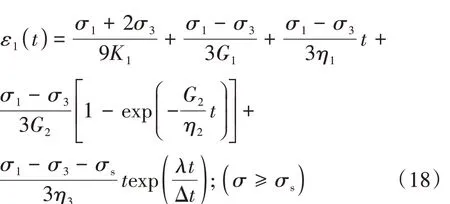
2 非线性蠕变损伤模型验证

为了得到合理的蠕变模型参数，本研究引入向家坝挤压带岩石三轴压缩蠕变试验数据［7］，采用Levenberg-Marquardt算法并结合Origin数值分析软件，对非线性黏弹塑性损伤模型进行拟合，可反演得到模型参数。为了便于非线性蠕变损伤模型与三轴压缩蠕变试验数据的拟合，将式（18）做系数简化，简化结果如式（19）。

表1 为三轴压缩蠕变模型参数。由表1 可知，不同应力水平下非线性黏弹塑性损伤模型的拟合相关系数R2均大于0.971，验证了模型的合理性。图3 为围压在2.0 MPa 状态下三轴压缩蠕变试验结果与拟合结果对比。

表1 三轴压缩蠕变模型参数

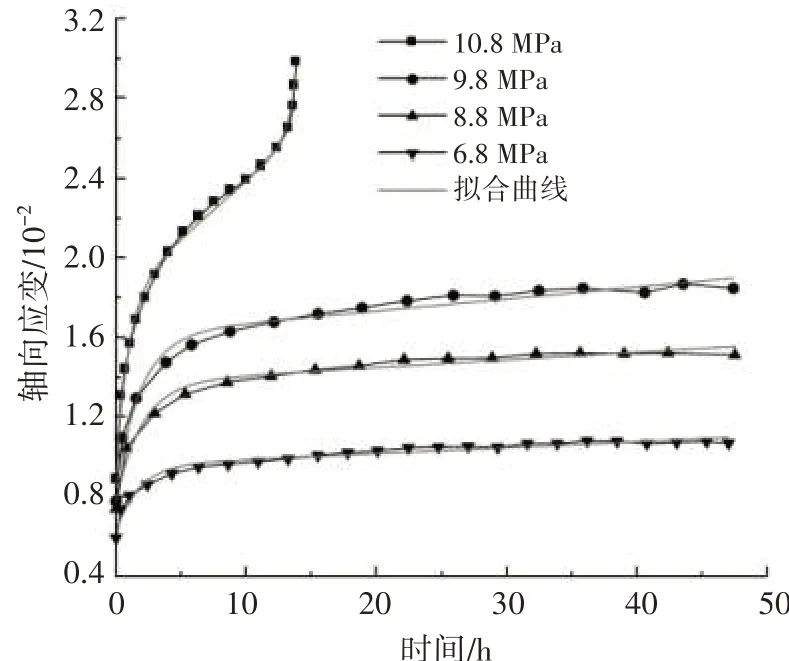
图3 三轴压缩蠕变试验结果与拟合结果对比

由图3 可知，试验数据均匀分布在拟合曲线两侧，尤其在岩石加速蠕变阶段，非线性蠕变损伤模型拟合结果与试验数据基本一致，表明该模型弥补了伯格斯模型难以描述加速蠕变阶段的不足，证明了本研究建立的非线性蠕变损伤模型用于描述不同应力水平下的蠕变特征较为合理。

3 结论

①通过对伯格斯模型蠕变特征分析，结果表明伯格斯模型能较好地描述岩石瞬时弹性变形、减速和等速蠕变阶段，难以描述加速蠕变阶段。根据损伤演化规律建立了黏塑性损伤体并给出了损伤演化方程，用以描述由于损伤积累引起的加速蠕变特征。将黏塑性损伤体引入伯格斯模型，得到非线性蠕变损伤模型。

②采用不同应力水平下三轴压缩蠕变试验数据对非线性蠕变损伤模型的合理性和适用性进行验证。结果表明，非线性蠕变损伤模型能较好地描述岩石蠕变全过程，弥补了伯格斯模型难以描述加速蠕变阶段的不足。