正态分布曲线在轴类零件生产线FTT的应用

肖 芝 凌 旭 戴俊良

（湖南化工职业技术学院机电工程学院，湖南 株洲 412000）

0 引言

首次合格率（First-Time-Through，FTT）是目前国际上监控生产线产品质量的一项重要的精益生产指标，是指一次性完成一个生产过程满足质量要求的零件的百分率。例如，某一机加线包括工序1车、工序 2 铣、工序 3 钻、工序 4 磨这四道工序，那么该线体的总体首次合格率为每道工序的首次合格率的乘积，可表示为FTT总=FTT1×FTT2×FTT3×FTT4，要注意的是，返工返修后的合格品不计入合格数。提升生产线的FFT 能有效降低生产过程的质量成本。正态分布即正常状态下的随机变量分布，影响随机变量取值的各个因素都不起主要作用，且各个因素相互独立，则该随机变量服从的是正态分布。例如，人的身高体重、某班级期末考试成绩、田里水稻的产量等。在机械制造业中，正态分布的应用也比较广泛，特别是在质量管理方面，如零件加工尺寸分析、检验员的测量误差分析、测量系统的误差分析等。通过正态分布曲线不仅能预算批量生产加工零件的FTT、判定加工设备的工序能力，还可分析机械制造过程中加工误差的性质，从而提升加工质量。

1 FTT的计算与分析

某涡轮增压器转子轴的机械加工生产线共有10 道工序，即工序1（钻中心孔）、工序2（双刀架粗车加工）、工序3（小径磨削加工）、工序4（密封槽的磨削加工）、工序5（大径磨削加工）、工序6（涡轮轮廓磨削）、工序7（去毛刺）、工序8（动平衡）、工序9（激光打标）、工序10（检验入库）。其中，工序3、工序6为关键工位。

对现场收集到的当日报表数据进行统计，当天共投入毛坯215 件，产出合格件214 件，合格率为99.53%。在各工序中，工序1、工序2、工序4、工序6、工序 7、工序 9、工序10 的 FTT 均为 100%，工序 3 返工10件，工序5返工1件，工序8报废1件。根据FTT的计算方法，则FFT=100%×100%×95.35%×100%×99.53% ×100%×10总0%×99.53%×100%=94.45%。合格率与首次合格率间的差异在于返工数，大量的返工零件不仅增加整个流水线的时间节拍、降低生产效率，还在一定程度上扰乱整个生产节奏，使生产管理的难度进一步提高。从上述分析可以看出，工序3（小径磨削加工）是制约FTT 提升的关键工序。

2 数据收集及正态分布曲线分析

2.1 数据收集

工序3 为轴径尺寸的磨削精加工，其尺寸要求为ϕ4.11+00.005，精度等级高，直接影响产品的性能及可靠性。因此，对该工位的尺寸质量进行严格管控，通过通止规进行百检。为了提升工序3 的FTT指标，从库房中随机选取首次合格的50件203零件进行尺寸测量，并随机从工序3返工的10件零件中抽取2 件返工前测量记录的尺寸数据，共52 组数据，见表1。

表1 工序3轴径尺寸测量值

2.2 正态分布曲线

正态分布的函数形式见式（1）。

式中：σ 为样本标准差；x 为样本均值；x 为随机变量；f（x）为发生xn随机变量的概率。

其中，样本均值x 和样本标准差σ 的计算公式见式（2）、式（3）。

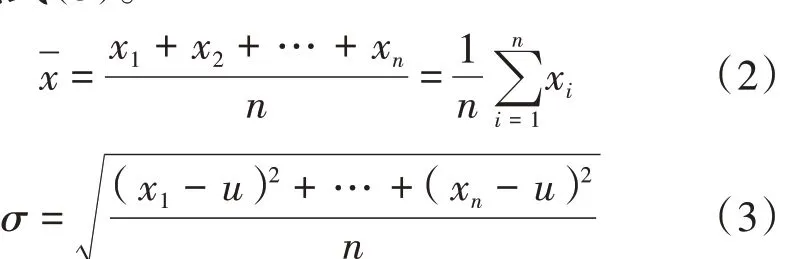
由正态分布函数的表达式可知，正态分布曲线是由平均值x 与标准差σ 来决定的，令f（x）=y，以y为纵坐标，x为横坐标，正态分布曲线见图1。

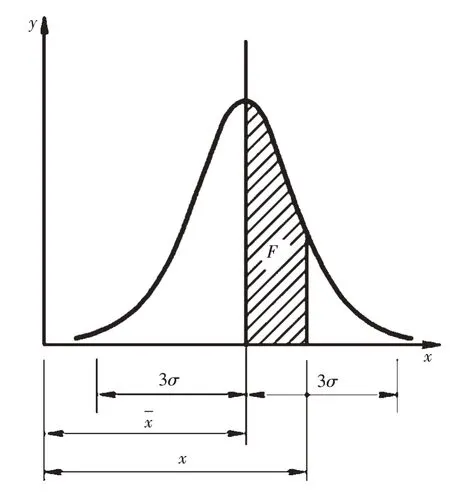
图1 正态分布曲线图

正态分布曲线与x轴所包含的图形面积为全部随机变量出现的概率，其总面积为100%，见式（4）。

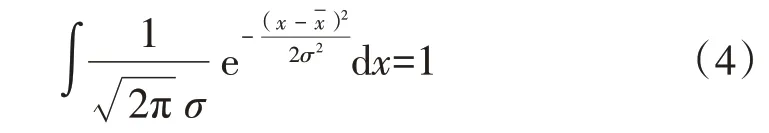
在图1 中，F 区域的面积表示某随机变量x 测量值到总样本平均值x 之间数值区域出现的概率值，计算公式见式（5）。

计算出Z 值，通过标准正态分布概率表即可得出F值。

2.3 正态性检验

在对数据进行正态分析前，要检验收集到的数据的正态性。本研究使用质量统计分析软件Minitab 对表1 中数据的正态性进行检验。将52 组测量值作为被检验的随机变量，检验方法选择Ryan-Joiner。检验结果P值>0.05，可认定该数据服从正态分布。其中，数据样品的均值x=4.114 17、标准差σ=0.000 785 2，如图2 所示。如果出现数据类型不服从正态分布的，可检查数据样本量是否过少或数据中存在随机误差［1］。

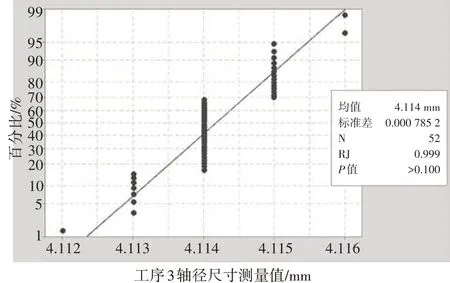
图2 正态性检验

2.4 工序能力判定

工序能力指数是判明工序的实际加工精度能否满足公差要求的程度指标，用Cp来表示。Cp=控磨床的工序能力。工序3 中所加工零件的尺寸公差为0.005 mm，根据2.3 中所得标准差σ=0.000 785 2，可得工序3 的工序能力指数Cp=1.061。根据表2可判定工序3卧式数控磨床设备的工序能力一般，属二级工艺，基本能满足轴径磨削的加工精度［2］。

表2 工序能力等级

2.5 整体样本合格率预测

根据正态分布的特征，限值为4.110～4.115 mm（工序3 加工轴径的尺寸下上偏差值）的正态分布曲线与x 轴所围成的区域面积即为整体样本的合格率［3］。可将整体样本合格率以平均值x为界分为左右两部分区域，分别计算二者的面积，如图3所示。

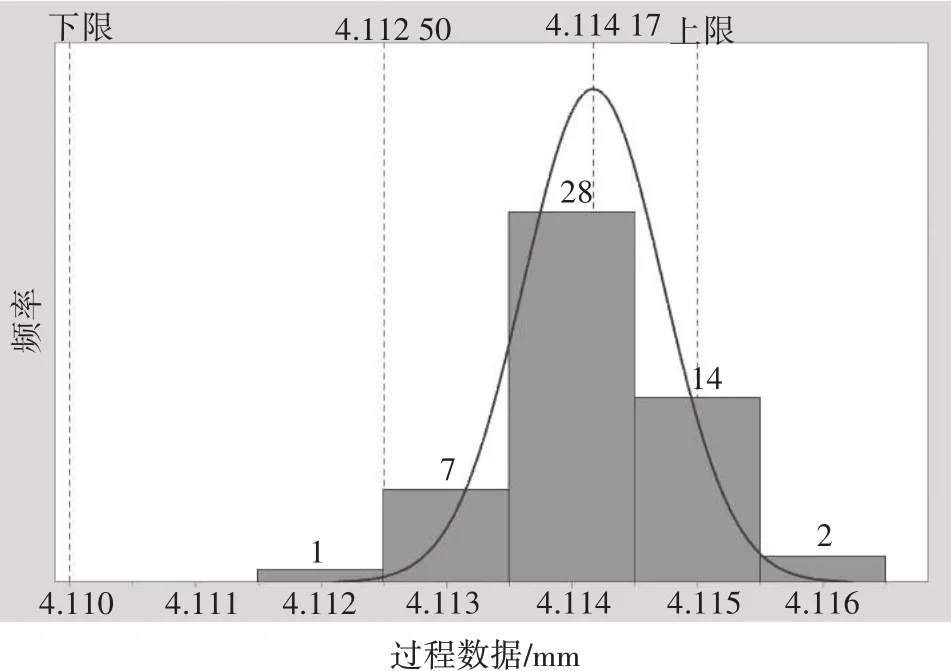
图3 工序3测量数据正态分布曲线

4.114 17～4.115 mm（上偏差至x）的区域面积可通过公式（6）计算得到，即Z=（4.115-4.11417）/σ=1.057，查询标准正态分布概率表可得右边区域面积=0.7109/2=0.355 45，合格率即为35.55%。同理可计算出左边区域面积为0.5，合格率即为50%，整体样本的合格率等于左右两部分区域面积之和，即整体样本合格率为85.55%，即为整体样本FTT 预测值，这与2.1 中的FTT 计算值95.35%有差异，这跟FTT 样本数据量的大小有关，只要FTT 的样本量足够大，其值一定趋于95.35%。

2.6 问题排查及改进措施

从图2正态分布曲线图可以看出，实际尺寸测量平均值x=4.114 17 mm，与理论平均值4.112 5 mm相差0.00167 mm，实际分布曲线向左偏移了0.00167 mm。如果正态分布曲线未发生偏移，FTT 计算值为99.72%。因此，导致FTT数据指标下降的直接原因为平均值数据发生了偏移。

出现偏移的主要原因有2 个。一是加工过程中砂轮的径向进给量过于保守，二是砂轮的修正频次（每10件修正1次）过低。由于企业生产任务紧，考虑生产效率，暂不对砂轮的频次改进修正。因此，提升FTT 的改进措施为适当增加磨削径向进给量［4］。

3 问题跟踪及验证

根据2.5 中正态分布曲线偏移量0.001 67 mm，将改进措施中的参数设定为在原有磨削径向进给量增加0.001 5 mm，并试验跟线一天，统计FTT值。

3.1 数据统计

据现场统计的数据，当天共投入试验毛坯218件，产出合格件216 件，合格率为99.08%，FTT=98.63%123总。在各工序中，工序 、工序 、工序 、工序4、工序6、工序7、工序9、工序10的FTT均为100%，工序 5 返工 1 件，工序 8 报废 2 件。可得出工序 3 的FTT=100%，跟实施改进措施前有较大的提升，达到预期效果。为得到进一步数据进行理论验证，随机抽检52件零件，并对工序3加工的轴径尺寸进行测量，测量数据见表3。

表3 改进后工序3轴径尺寸测量值

3.2 正态性检验

根据2.3 中的步骤，可得出正态性检验结果，P 值>0.05，可认定该数据服从正态分布，其中数据样品的均值x=4.113 25，标准差σ=0.000 789 0，如图4所示。

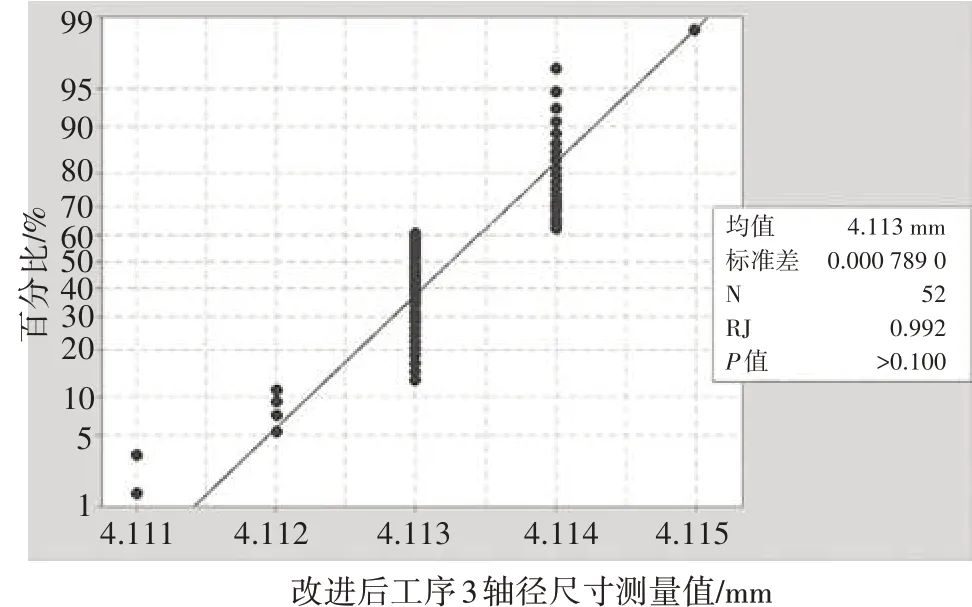
图4 改进后尺寸数据的正态性检验

3.3 改进后整体样本合格率预测

图5 为改进后测量数据的正态分布曲线，其均值相对理论正态分布曲线中心4.112 5 mm，向左偏移0.000 75 mm。根据2.4 中的计算过程，整体样本合格率为98.65%，即FTT=98.65%，相比改进前提升了近13个百分点，取得良好效果［5］。

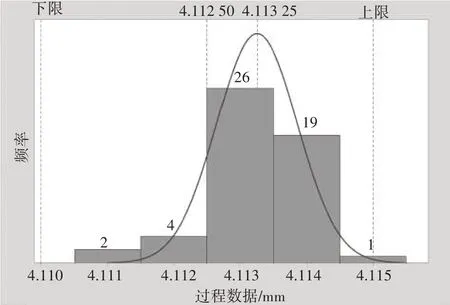
图5 改进后测量数据正态分布曲线

4 结语

本研究通过对正态分布曲线进行分析，可有效提升某涡轮增压器转子轴机械加工生产线的FTT值，可大幅度降低大批量生产线的质量成本。为正态分布曲线在解决实际生产过程中的产品质量问题提供理论与实践依据。质量管理要以实际生产数据为依据，运用数理统计等相关理论知识对生产过程中各个要素进行分析，从而不断提升产品质量。对工序3 的工序能力Cp值，可根据企业实际情况进行提升，由于影响产品质量的因素复杂，一旦某个因素发生变异，出现不合格品的风险将增加。适当提高砂轮的修正频次是不错的提升措施。