基于全绕组拓扑结构的移相变压器建模及应用

李晓华，陈镇生，罗一杰，刘 玮，屠卿瑞

（1. 华南理工大学 电力学院，广东 广州 510640；2. 广东电网有限责任公司电力调度控制中心，广东 广州 510600）

0 引言

移相变压器具有控制电网有功潮流、消除环网电磁环流、提高断面输送的能力，因此受到了国内外学者的广泛关注［1］。作为国家能源局“十四五”规划中提升大型输电通道利用率的重要手段之一，移相变压器在我国有着巨大的工程运用前景［2］。其独特的串接方式和工作特性与传统变压器大不相同，接入电网后势必会对系统保护提出新的挑战。而保护整定的核心问题在于各类短路故障下的电气量计算，现有模型却是建立在系统对称稳态的基础之上，并不能用于各类故障下电气量的求解。因此需要建立适用于各种端口故障情况下电气量求解的数学模型。

目前国内外学者已对移相变压器在本体结构设计［3］、在线融冰［4］等应用方面进行了相关研究。对其故障分析的研究多集中在对称稳态数学模型、本体保护方法、对系统影响等方面［5］，并没有考虑当系统发生扰动时，移相变压器的等效模型及电气量求解问题。文献［6］和文献［7］根据对称双芯式移相变压器ST-PST（Symmetrical Two-core Phase-Shifting Transformer）的连接结构和电磁约束关系，推导出其稳态等效模型。文献［8］进一步利用此模型推导了负载条件下有载分接开关的级电压计算公式，并分析了级电压的变化规律及影响因素。该类文献虽然分析了移相变压器的基本工作原理和分接开关随负载的变化情况，但以系统正常稳态运行为前提，并没有分析系统短路故障下的运行情况。文献［9］针对原有差动保护的缺点提出了一种数字化的移相变压器保护方案。文献［10］提出了一种基于方向性比较的移相变压器保护方法。文献［11］提出一种基于零序电流的匝间保护新原理，通过构建自适应动作门槛和制动量，极大地提高了保护的灵敏性和可靠性。文献［12］提出一种新的保护算法，可以对故障进行有效定位和分类。文献［13］根据移相器的工作原理，分析了移相变压器的加入对原有系统纵联保护的影响。此类文献对移相变压器的研究主要在于保护原理本身的适用性，而电气量是基于测量或是系统参数对称进行设置，对于复杂情况下的电气量求解并没有涉及。

综上，现有关于移相变压器的研究缺乏一套综合考虑转角和内阻抗并适用于不对称运行和内外部故障下电气量求解的数学模型。为了更好地对移相变压器本体保护及与之临近线路的保护适应性展开分析，本文以工程中广泛应用的ST-PST 为例，根据其绕组结构和电磁约束关系建立了全相数学模型［14⁃18］。以某220 kV ST-PST 为例验证了模型的准确性，并进一步利用该模型分析了不同相序下阻抗和移相特性，为移相变压器故障计算与保护分析奠定基础。

1 ST-PST拓扑连接及电路模型

ST-PST 由串联变压器（简称串联变）和并联变压器（简称并联变）构成。串联变绕组的连接方式为Ⅲ／△，其一次侧绕组纵向接入网侧，且带有中间抽头连接并联变的一次侧，其接入方式和运行特点与传统变压器差异较大。并联变的连接方式为Yn／Yn，其二次侧与串联变二次侧相连且具有不同的分接头档位，用于调节输出电压的角度。ST-PST 的整体连接方式如图1 所示。图中：UIx、UOx（x=A，B，C）分别为移相变压器的x相输入、输出电压；USPx为串联变的x相输入电压；UP2Lx为并联变的x相输出电压。根据图1中ST-PST的连接关系可得其全相等效电路如附录A图A1所示。

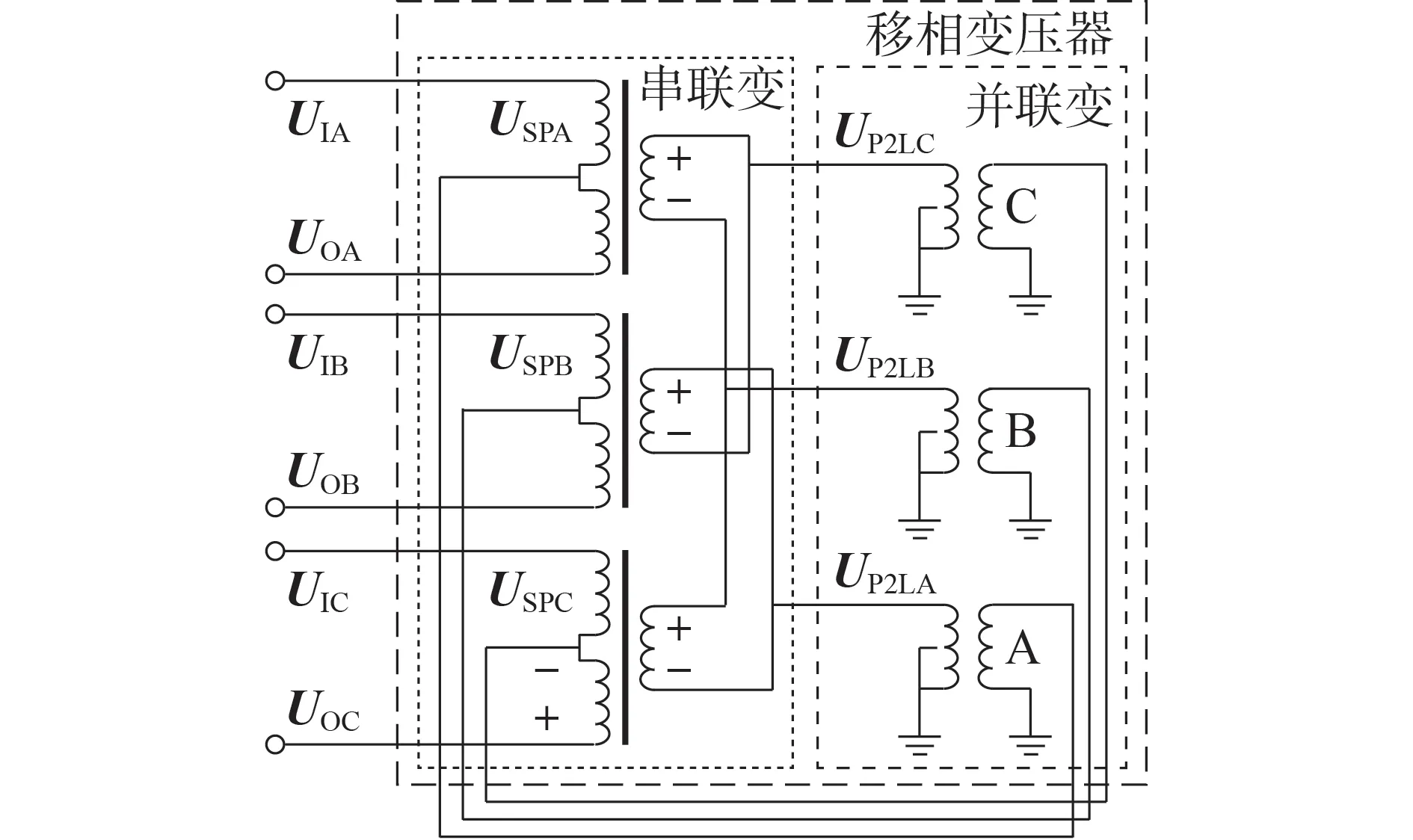
图1 ST-PST的连接图Fig.1 Connection diagram of ST-PST

2 ST-PST的数学模型

2.1 稳态数学模型及存在的问题

2.1.1 对称运行时ST-PST稳态数学模型

对称运行时ST-PST可由1个理想的移相器串联1 个阻值随分接档位改变的阻抗Z构成，如图2 所示。图中：α0为空载时输出电压与输入电压的移相角度差，该角度的大小可由式（1）求得；UI、II分别为输入电压、电流；UO、IO分别为输出电压、电流；为空载输出电压；Z为等效漏阻抗；R、X分别为等效漏电阻、等效漏电抗。关于等效漏阻抗Z的求解，文献［6］进行了详细推导，本文不再叙述。

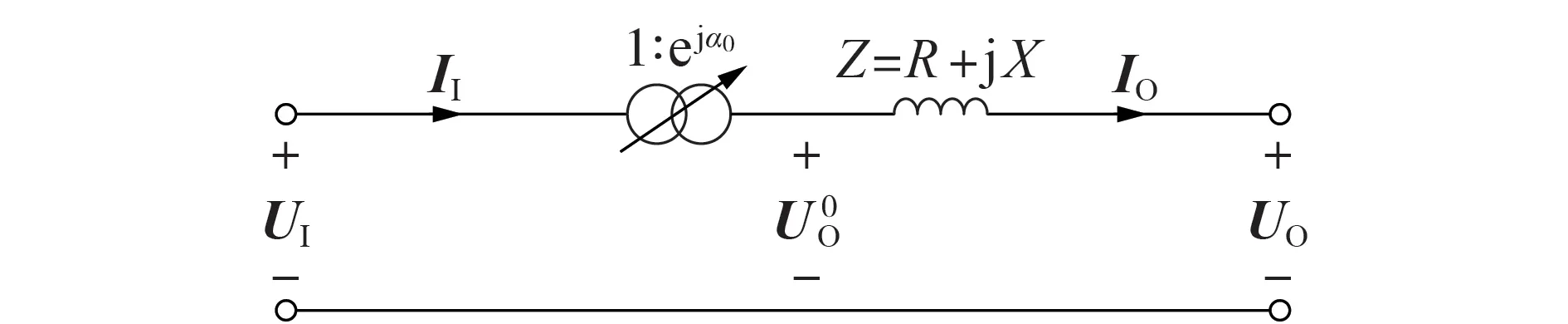
图2 对称运行时ST-PST的等效电路Fig.2 Equivalent circuit of ST-PST in symmetrical operation

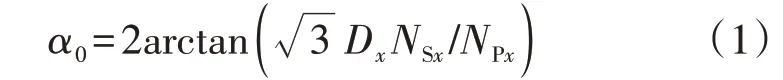
式中：NSx、NPx分别为串、并联变的变比；Dx为并联变二次侧的接入绕组匝数与总匝数之比。负载运行时由于Z的存在导致输出电压UO会有幅值和相角的偏移，记偏移的角度为θ，当负载阻抗角为φ时，θ的计算公式如式（2）所示。

此外，滞后调节时电压、电流运行相量图见附录A图A2。

2.1.2 问题分析

串联变的连接方式为Ⅲ／△，与传统变压器截然不同。并联变为不常见的Yn／Yn连接方式，且输出电压具有一定的转角关系。现有ST-PST 模型仅针对系统稳态对称情况下的电气量计算［6］，并不能用于计算不对称故障下的电压、电流。其次，当STPST 内部端口处发生短路故障时，三相之间具有耦合性，并不具有独立性，无法用单相等效表征三相，且从外部难以进行等效。

针对现有数学模型的局限性，本文利用相分量法对ST-PST 进行建模。首先，根据电磁约束关系推导出描述串联变Ⅲ／△连接和并联变Yn／Yn连接关系的导纳矩阵；再根据节点合并方法，对串、并联变的特殊拓扑连接方式进行合并处理，得到ST-PST 的导纳矩阵；最后，根据故障情况对矩阵进行修正并求取节点电压，再由节点电压求取各支路电流。所建模型适用于端口各种短路和断路情况下的电气计算，不依赖于系统是否对称，并将具有移相功能的电磁耦合回路等效为电气上直接相连的等值电路，具有良好的工程运用性。

2.2 相分量法数学建模

为了更好地建立ST-PST 的全相数学模型，对附录A 图A1所示等效电路进行节点编号的定义，其简化拓扑节点定义见附录A图A3。

2.2.1 并联变的导纳矩阵

ST-PST 的并联变由3 个双绕组变压器连接而成，根据图A3 可得并联变所涉及的节点编号，见附录A图A4（a）。以A相为例，根据电磁约束关系可以得到节点注入电流与电压的关系如下：

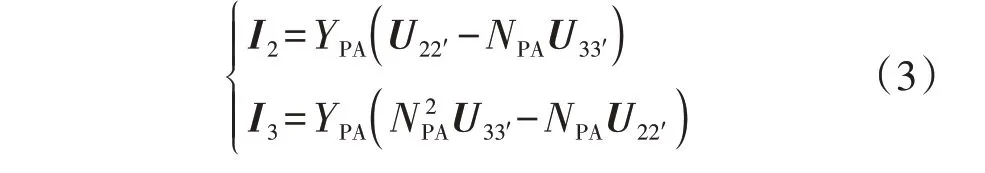
式中：YPA=(ZP1A+ZP2A)-1，NPA为A 相并联变的变比，ZP1A、ZP2A分别A 相为并联变满档时的一、二次侧漏抗；I2、I3分别为A相节点2、3注入电流；U22'、U33'分别为A 相节点2、2'和3、3'间电压。则可以得到A相节点2、2'和3、3'的导纳矩阵YP1为：

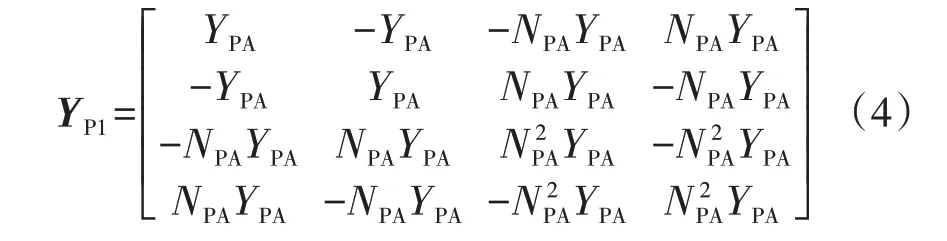
YP1中的行（列）元素从左（上）到右（下）表示的节点依次为2、2'、3、3'，主对角线元素表示自导纳，非对角线元素表示互导纳。进一步可得A 相等效电路图如附录A图A4（b）所示。

同样对B、C 相做上述处理。记并联变的B 相导纳矩阵为YP2，C相导纳矩阵为YP3，YP2、YP3的矩阵表达式见附录A 式（A1），则并联变的不定导纳矩阵YP的计算式见式（5），YP的具体表达式见附录A式（A2）。

2.2.2 串联变的导纳矩阵

串联变由3 个三绕组变压器构成，其等效电路、节点编号和电流编号见附录A图A5（a）。

同样根据电磁关系可得到节点注入电流与电压之间的关系，以A相为例，其矩阵YS1表达式为：

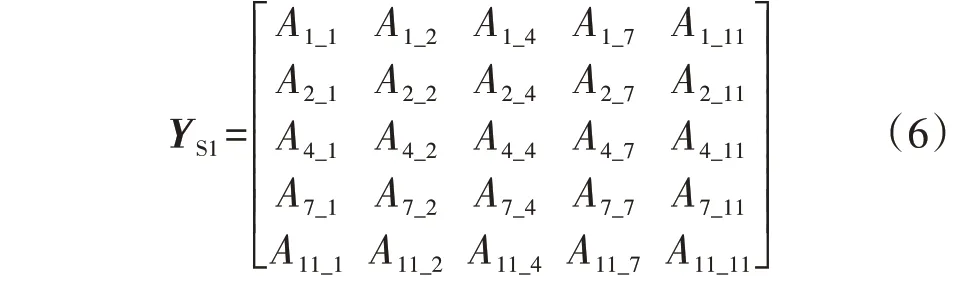
YS1为对称矩阵，上三角元素表达式为：

式中：ZS1A—ZS3A为A 相串联变的3 个绕组的等值漏抗；NS1A、NS2A分别为A 相串联变绕组1-3 和绕组2-3间的变比。根据A 相导纳矩阵，可以得到A 相等效电路模型，见附录A图A5（b）。

串联变B、C 两相亦可以进行类似处理，分别将导纳矩阵记为YS2、YS3，其表达式分别见附录A 式（A3）、（A4）。则串联变的不定导纳矩阵YS的计算公式如式（9）所示，其具体的表达式见附录A式（A5）。

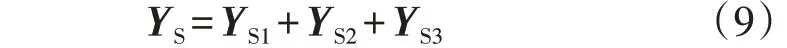
2.2.3 串并联节点合并及系统接地处理

根据相分量法中节点i与节点j的合并方法，将第j行和列加入第i行和列，并删除矩阵中节点j的行和列。合并后的数学表达式为：

ST-PST 中串联变与并联变的连接关系可以简化为附录A 图A6 所示。根据上述处理方法对需要合并的节点进行处理，便得到ST-PST 的导纳矩阵YPST0。

系统节点接地电压箝位为0，电压从待求量变为已知量。根据相分量法中接地节点的处理方法，删去电压向量中此节点对应元素。即删去导纳矩阵相应的行和列，形成n-1 阶的导纳矩阵。节点i接地后矩阵如式（11）所示。

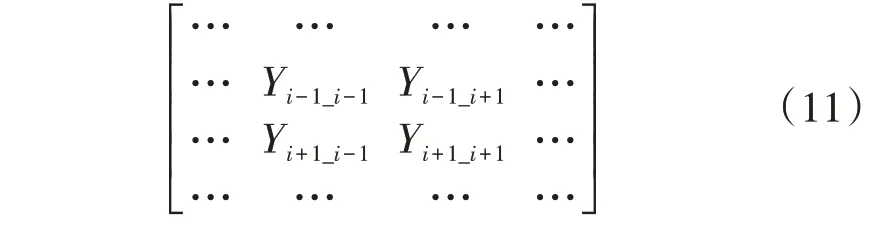
利用节点接地处理方法，对矩阵YPST0中接地节点的行列进行删除，得到ST-PST 的导纳矩阵YPST，其表达式见附录A 式（A6）。从附录结果可以看出YPST为12×12 阶的矩阵，为叙述方便，记YPST如式（12）所示。

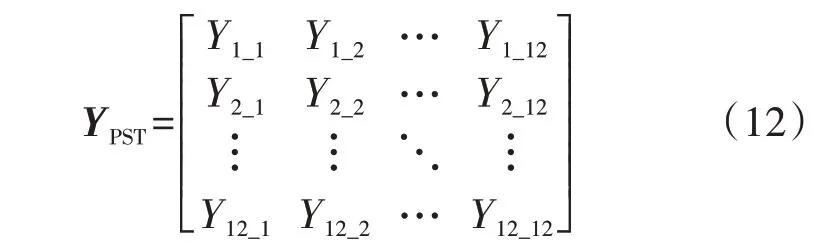
根据ST-PST 的导纳矩阵可以得到其全相等效电路模型，如附录A图A7所示。

2.3 不同故障情况下ST-PST的矩阵修正

当系统发生故障时，需要对故障涉及节点所对应的矩阵元素进行修改。ST-PST 加入线路后的等效电路图如图3 所示。图中：U1、Z1和U2、Z2分别为两端电源的电压和等效阻抗；M、N分别表示ST-PST接入线路的点M、N；Zline为线路等效阻抗。

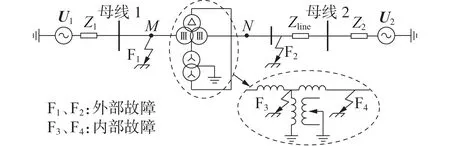
图3 ST-PST内外部故障示意图Fig.3 Schematic diagram of ST-PST internal and external fault

图3 标注了ST-PST 不同故障发生的位置，F1、F2为外部故障，F3、F4为内部端口故障。以故障F3为例，矩阵元素修改如表1 所示。表中：发生故障F3涉及的节点编号为2、6、10；Zfault为故障过渡阻抗。表中给出了发生典型故障时的矩阵元素修改方法，发生断路故障时两节点间的阻抗应为无穷大，但为满足程序计算和工程允许误差，本文取1010表示无穷大阻抗。另外，由于发生匝间故障时的情况较为复杂，本文模型暂未考虑匝间故障的计算。

表1 不同故障类型的矩阵修正Table 1 Matrix correction for different fault types

3 模型验证与应用

本文以某220 kV 的ST-PST 参数为例，在PSCAD／EMTDC中搭建了图3所示仿真模型，两端电源参数为220∠0°kV，电源等效阻抗为0.75+j3.95 Ω，线路阻抗为0.36+j1.86 Ω，ST-PST 技术参数见附录A表A1。

根据上述建模方法编写计算机程序，得到系统模型的导纳矩阵，求取上文中各节点电压和支路电流。对比故障稳态时的PSCAD 仿真数据和程序计算结果，对本文建模的正确性和有效性进行验证。此外，利用本文所得数学模型详细分析其在不同相序下的等效阻抗和移相特性，并得到其在不同相序网络中的等效电路。

3.1 不对称稳态电气量验证

根据图3 所示4 处故障，在1%励磁电流情况下，分别对比PSCAD 仿真数据与本文方法计算数据。限于篇幅，本文以内部故障F3为例，故障阻抗大小设为1、10、100、1000 Ω，图4中给出了三相输出电压在不同阻抗类型下计算值与仿真值的最大误差百分比。由图4 可以看出故障下仿真结果与计算结果误差均较小，在0.1%以下，验证了模型的准确性。

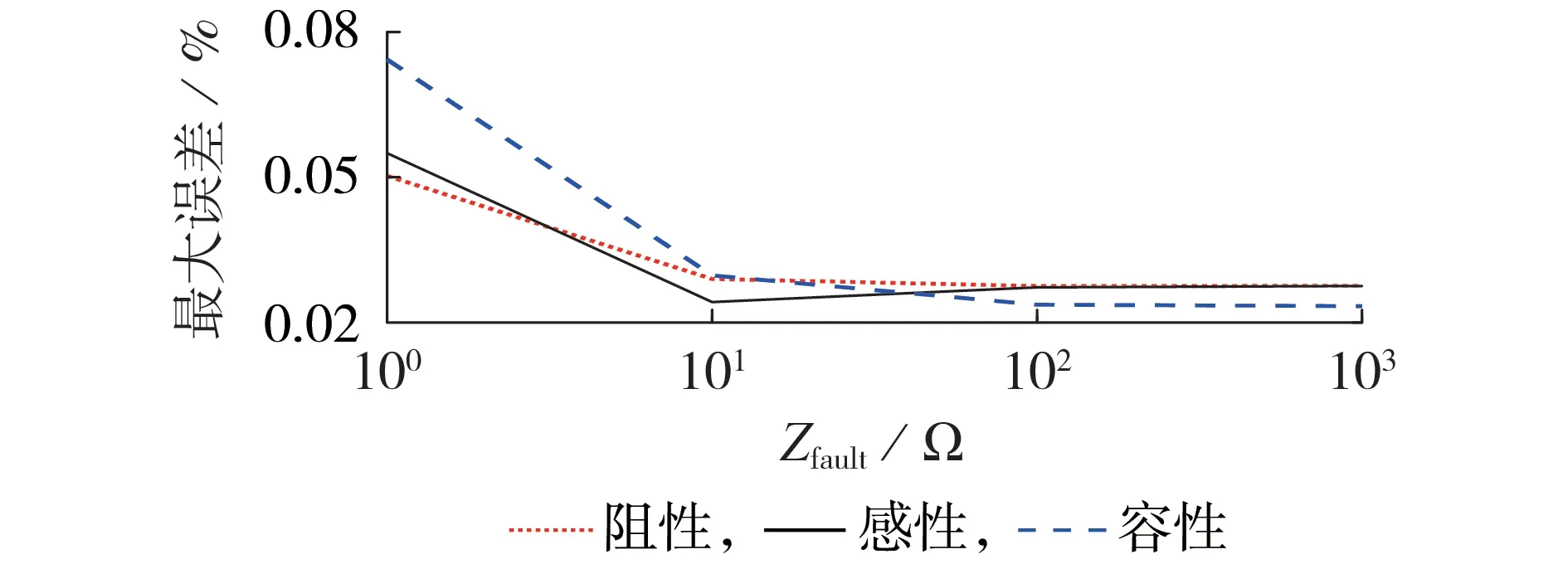
图4 当F3为A相接地故障时仿真与计算值的最大误差结果Fig.4 Results of maximum error between simulative and calculative values when F3 represents phase-A ground fault

3.2 模型在相序特性分析中的应用

3.2.1 相序阻抗分析

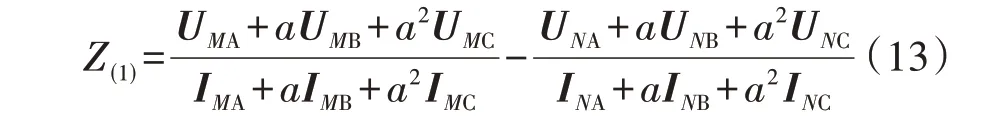
当F1处发生4 种典型故障时，利用本文方法进行计算，求取图3 中点M和点N的三相电压、电流值，根据测量结果求取序分量，再求取序阻抗。以正序阻抗为例，其计算方法见式（13），正、负、零序阻抗（Z(1)—Z(0)）大小的计算结果如图5所示。式中：Z(1)为正序阻抗；a为旋转因子，a=1∠120°；UMx、IMx和UNx、INx分别为点M和点N的x相电压、电流。图5 所示的阻抗大小综合了4 种典型故障计算结果。由图可知：ST-PST 的正负序阻抗相等且随着档位增加而增加；零序阻抗与档位无关，三序阻抗在零档时相等。

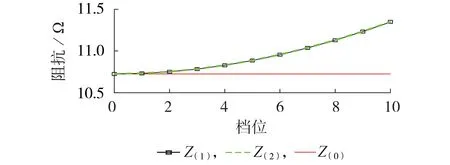
图5 不同档位下的相序阻抗大小Fig.5 Phase sequence impedance at different gears

3.2.2 相序移相特性

同样以F1表示的4 种典型故障为例进行计算，进一步分析不同档位下ST-PST 对相序电压的移相特性。由于等效内阻的存在，会改变输出电压相角，但对电流没有影响，因此利用电流对相角特性进行分析。以正序滞后为例，正序移相角α(1)的计算方法如式（14）所示，综合计算结果如图6 所示，图中α(2)、α(0)分别为负序、零序移相角。由图可知，ST-PST 的移相特性在三序中并不一致，若正序为滞后，则负序为超前，反之亦然。对于零序而言，其移相角为0°，并没有移相作用。

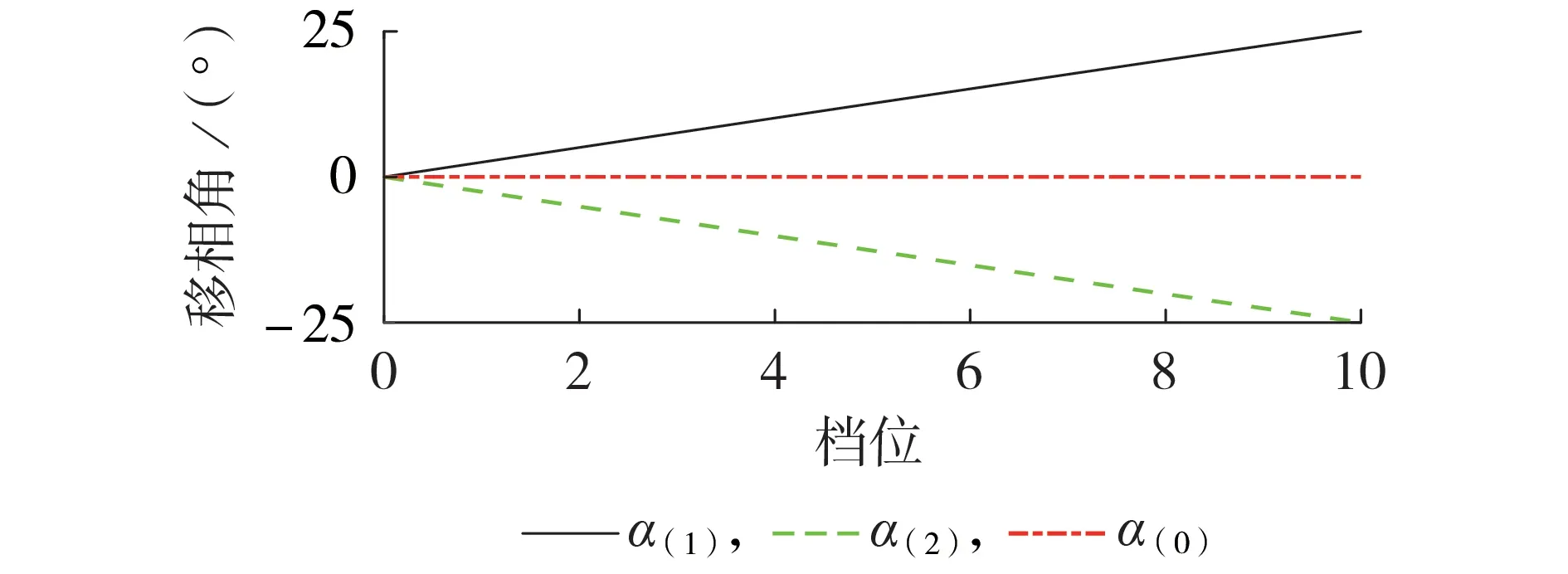
图6 不同相序下的移相特性Fig.6 Phase-shifting characteristics in different phase sequences

式中：angle（·）为相角求取函数。

3.2.3 相序等效电路

上述结果表明，ST-PST 在不同序网络中的等效模型不同。利用本文所述模型可得相序等效电路如图7 所示。图中，I（1）、I（2）、I（0）和U（1）、U（2）、U（0）分别为正、负、零序电流和电压。

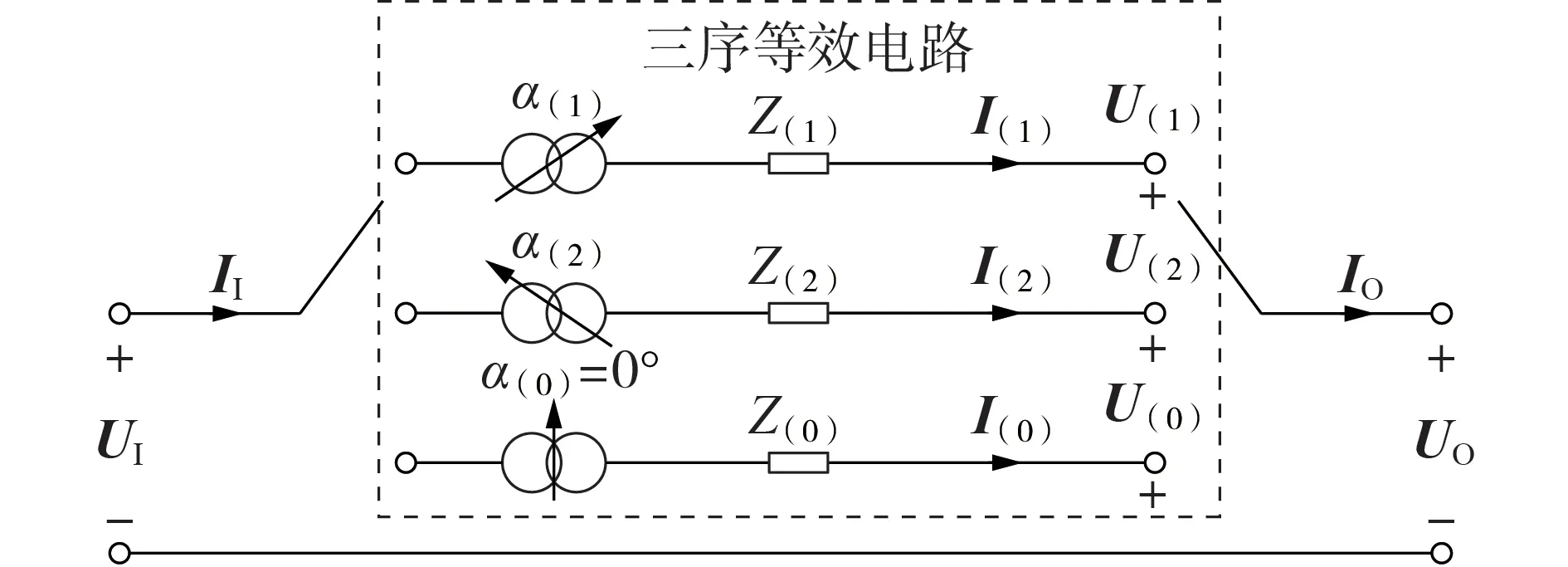
图7 ST-PST的三序等效电路Fig.7 Phase sequence equivalent circuit of ST-PST

图7 中阻抗和移相角的计算公式如下：

由此可得ST-PST 的三序特性：正负序相角调节相反，但阻抗一致，阻抗大小与ST-PST 的等效漏阻抗和变比均相关；零序下没有相角调节作用，可等效为1 个恒定阻抗，其大小仅与串联变参数相关。因此，在含有移相变压器的系统保护中需要考虑其相序特性的不同。

4 结论

针对现有ST-PST 数学模型并不能适应内外部不对称运行状况的问题，本文应用相分量法推导了ST-PST 的数学模型，并利用该模型分析了不同相序下ST-PST的运行特性。经实例验证，主要结论如下。

1）针对现有数学模型的不足之处，应用相分量分析法得到了ST-PST 的全相数学模型，并基于实例验证了模型的准确性。该方法不受限于移相变压器的拓扑结构、不依赖系统运行状况，能适应各种端口短路、断路故障情况下的电气量计算，便于工程运用。

2）不同相序下移相变压器的运行特性不同：正负序在不同档位下的等效阻抗虽然一致，但移相特性却相反；零序下移相变压器可等效为恒定阻抗，阻值不随档位变化而变化，且并不改变电压相角。

附录见本刊网络版（http：//www.epae.cn）。