一种基于谐波补偿的级联H桥光伏并网逆变器控制策略
袁义生,朱启航,吕 森,刘 伟,张执钦
(华东交通大学 电气与自动化工程学院,江西 南昌 330013)
0 引言
近年来,新能源发电得到了长足发展。其中光伏系统的种类也日趋多样化,主要集中在2 个方向:高压大功率集中式光伏电站、分布式“户用型”光伏系统[1]。其中分布式“户用型”光伏系统拓扑选择较多,一般需遵循如下几个原则:①无变压器,转换效率大于96%;②单相或三相中低压并网;③体积小,重量轻,便于安装等。因此,级联多电平逆变器在光伏系统中的应用逐渐受到人们的关注[2]。相比于传统的两电平逆变器,级联多电平逆变器降低了开关器件电压应力,在相同开关频率下,可大幅减小滤波电感体积和并网电流的谐波含量,且随着级联数目的增多,可实现无变压器并网[3]。
级联H桥CHB(Cascaded H Bridge)逆变器具有效率高、成本低、易于模块化等特点,现已被广泛应用于矿山、冶金、造纸等国民经济行业[4]。CHB 逆变器用于光伏产业时,光伏面板可直接作为逆变器的输入源,解决了CHB 逆变器需要多组直流电源的弊端。且各H桥相互独立,光伏面板可分别独立完成最大功率点跟踪MPPT(Maximum Power Point Tracking)。但若光伏面板受灰尘、落叶、维修后型号不匹配等影响,输入功率会出现相差较大的情况。由于各H 桥单元经串联后流过同一个电流,功率较大的单元可能进入过调制状态,进而导致并网电流畸变,系统不稳定,被强制离网处理[5⁃6]。
因此,如何扩大CHB 逆变器在功率不平衡下的稳定运行范围,抑制并网电流畸变,是目前的研究重点之一。对国内外涉及该领域的文献进行梳理归纳,大体分为以下几种策略。①有功占空比修正法[7]。该控制方法基于各单元光伏面板输出功率的大小修正占空比,但该控制方法调节范围较小,在功率极度不平衡时系统将过调制导致电流畸变。②优化的MPPT 法[8]。该控制方法通过提高过调制单元的电压给定值,使输出功率较大的单元退出最大功率点,从而均衡各单元之间的输出功率,但该方法会降低系统的发电量。③拓扑优化法[9]。研究此类方法的文献较为繁杂,大体思路是在CHB 拓扑的基础上,增加少量开关器件以增加电路的工作模态,但普遍存在推广较难、不易模块化级联、控制复杂等缺点。④无功补偿法[10]。将逆变器功率因数作为额外的控制对象,增加控制自由度。该方法可在本质上消除CHB 逆变器内在不稳定,但可变的功率因数会限制其应用场合。⑤谐波补偿法。通过向过调制单元注入谐波来解决过调制问题,如:3 次谐波补偿法THCS(Third-Harmonic Compensation Strategy)[11⁃13],利用方波最大调制度为4/π的思路,通过在过调制单元中注入一定量的3次谐波,使得单元调制度由1提高至1.155;准方波补偿法[14],通过补偿谐波将调制波补偿为准方波,但因为实际调制波为准方波,所含的谐波成分频谱范围宽,使得过调制单元输出共模电压的谐波成分更多,相应的非过调制单元输出共模电压的谐波成分也更多;箝位正弦波补偿法[15],通过补偿谐波将调制波补偿为限幅的正弦波,但该方法中额外引入了中间变量,且要进行查表计算,算法变得复杂,增加了控制器的代码实现难度,控制器响应时间长。⑥调制策略。通过改变调制方式来解决电流畸变问题,如:混合调制策略[16⁃17],用于解决级联整流器中的负载不平衡问题,但该方法并不能够实现光伏系统中直流侧电压的MPPT 且并没有分析该方法的适用范围;一种单电源的工作模式以及相应的调制策略[18⁃19],对于存在虚设单元的级联结构,该方法能够在具有单个直流源和虚设单元的级联系统中稳定工作,但是该方法仅针对2个H 桥串联的结构,扩展困难、控制复杂,其中电压平衡问题仍然是一个挑战,尤其是在功率不平衡条件下;基于功率平衡的同相配置梯形脉宽调制策略[20],通过选择合适的梯形波,提高CHB 逆变器输出电压基波的幅值,降低了开关损耗,延长了系统的使用寿命,提高了系统的可靠性;热补偿非连续脉宽调制策略[21],通过控制非连续脉宽调制的夹角,对功率分布变化下的热循环进行补偿,以降低老化电池功率模块中功率半导体的热应力。
既然方波最大调制度为4/π,那么可认为文献[13]提出的THCS 并未完全发挥出其最大潜力。基于此,本文提出了一种新型谐波补偿控制策略NHCS(Novel Harmonic Compensation Strategy)。首先,建立了CHB 并网逆变器的数学模型;其次,分析了单位功率因数运行下系统稳定域运行范围;在THCS 的基础上,提出了一种NHCS 来进一步提高CHB 逆变器的稳定运行范围,引入适当的3、5 次谐波至过调制单元中,使其调制波峰值始终不大于1,同时引入反向的谐波至剩余的各单元中,以抵消过调制单元中引入的谐波成分;最后,搭建了3 级CHB逆变器的仿真模型和实验样机,并验证了所提方法的正确性和有效性。
1 单相CHB逆变器数学模型分析
单相CHB 光伏并网逆变器拓扑如图1 所示。n个H 桥中每个模块由4 个开关管组成,且由光伏面板独立供电,交流侧通过滤波电感与电网连接。图中:us为电网电压;is为电网电流;uL为滤波电感电压;udcx(x=1,2,…,n)为各H 桥单元直流侧电压;uHx为各H 桥单元交流侧电压;iPVx为各光伏面板输出电流;iCx为电容电流;iHx为各H 桥单元直流侧电流;Tx1—Tx4为各H桥单元的开关器件;Ls、Rs和Cx分别为滤波电感、线路等效电阻和直流侧滤波电容。
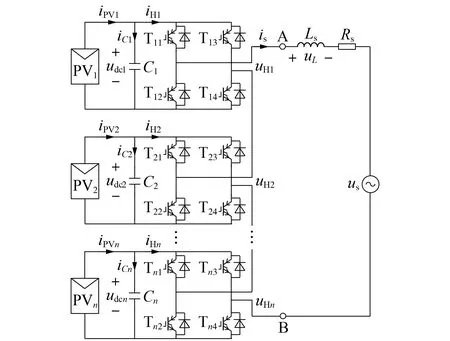
图1 单相CHB光伏并网逆变器拓扑Fig.1 Topology of single-phase CHB photovoltaic grid-connected inverter
由于损坏或遮挡,部分光伏面板的输出功率急剧下降,而其余光伏面板仍保持原有的输出功率,导致逆变器的总输出功率PT下降。由于电网电压有效值Us不变,电网电流is会减小。对于CHB 逆变器而言,所有的级联单元流过相同的电流,所以输出功率不下降的单元的输出电压会上升,导致调制波幅值增大,增加了过调制风险。
逆变器稳定运行时,可将第x个H 桥单元的调制波mx定义为:

忽略系统开关损耗、线路中的线阻等,根据基尔霍夫电压、电流定律,可列出交流侧数学模型为:
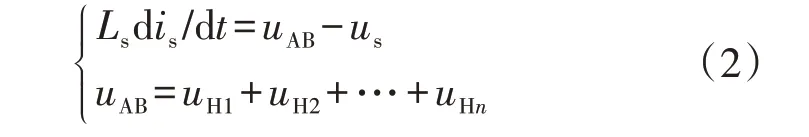
式中:uAB为逆变器交流侧电压。
结合式(1)与式(2),有:
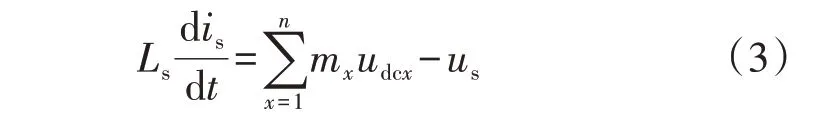
引入相量分析的方法,则式(3)的相量形式为:
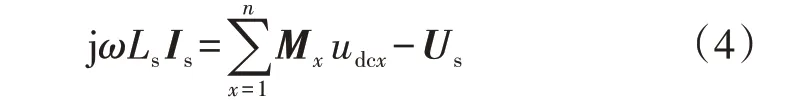
式中:Us、Is、Mx分别为us、is、mx的相量形式;ω为角频率。
当逆变器工作在单位功率因数时,相量图如图2 所示,由于电感的电压分量相比电网电压而言非常小,因此调制相角δ近似为0。
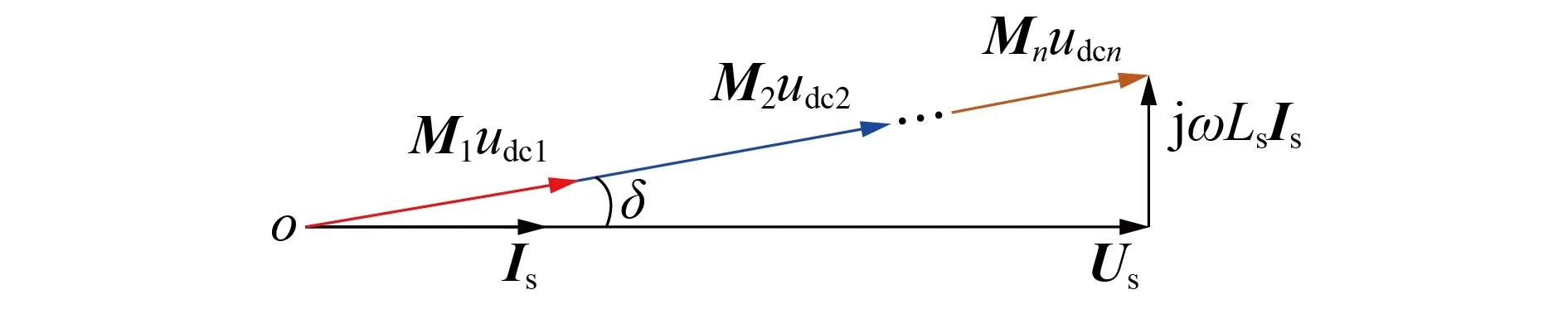
图2 单位功率因数运行下的相量图Fig.2 Phasor diagram of unit power factor operation
2 稳定域范围分析
单位功率因数下,各单元的调制波峰值保持在1 以下,即Mx≤ 2 /2 是CHB 并网逆变器稳定运行的前提条件。
定义第x个H 桥单元输送到电网的有功功率Px为:

式中:UHx为uHx的相量形式;Mx为第x个H 桥单元的调制波幅值。通常情况下,电感电压UL(即图2中的jωLsIs)远小于电网电压Us,因此,可近似认为cosδ≈1。根据式(5),可推导出Mx为:

根据Mx≤/2,有:
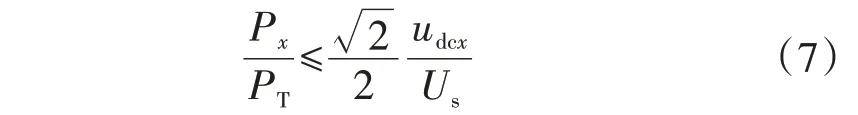
式(7)即为系统在单位功率因数下的稳定域约束条件。若第x个H 桥单元的功率和电压满足式(7)所示的关系,则其调制波mx的峰值会保持在1以下,系统运行在线性工作区内;否则该单元将会超调运行,向电网注入大量谐波电流,甚至导致逆变器失稳。
3 所提NHCS
文献[13]基于THCS 提出了一种用于单相CHB逆变器的控制策略,并且通过仿真和实验验证了THCS的有效性。当调制波为方波时,逆变器的调制度可达到最大值4/π。传统的THCS通过引入3次谐波将逆变器调制度提升至1.155,而1.155<4/π,因此可认为该方法未能完全发挥出谐波补偿的潜力。
3.1 所提NHCS的基本原理
本文在THCS 的基础上提出一种NHCS,引入5次谐波进一步发挥谐波补偿的潜力,则mx可表示为:
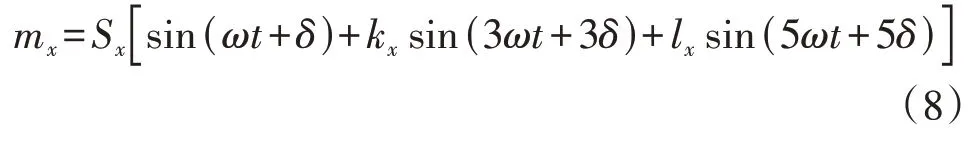
式中:kx、lx分别为3、5次谐波补偿系数;Sx为第x个H桥单元的调制度。
图3 为过调制单元的调制波中注入3、5 次谐波后的示意图,图中1.207 为NHCS 的最大能力范围。m1由基波分量mB1、3 次谐波分量mT1和5 次谐波分量mF1组成。可以看出,合成后的m1在保证峰值不大于1 的前提下,mB1的峰值达到了1.207。相较于THCS 的最大值1.155,逆变器超调扩展能力提高了33.55%。
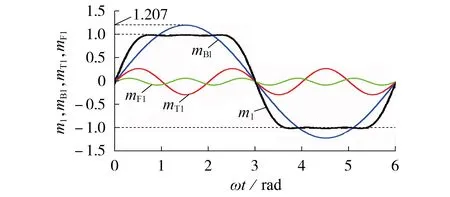
图3 调制波中注入3、5次谐波的示意图Fig.3 Schematic diagram of modulation wave injected by third and fifth harmonics
3.2 最优kx、lx的确定
图3 从理论层面表明5 次谐波的注入有助于提高逆变器的超调能力,但补偿系数kx、lx还有待确定。
为保证实现最小的补偿量,达到补偿系数刚刚好的目的,设补偿后mx的最大值正好为1,则Sx与kx、lx之间的函数关系可表示为:

根据式(9),Sx与kx、lx之间的函数关系如附录A图A1 所示,图中红色轨迹表示在最小5 次谐波的前提下,调制度所能达到的最大值。可以看出,当lx=0,即没有5 次谐波时,调制度Sx最大可至1.155。随着5 次谐波的注入,Sx先升后降,最高可升至1.207。附录A 图A2 为图A1 中红色轨迹的y-x视角,附录A 图A3为该轨迹中Sx与lx之间的对应关系曲线。
当1.155Sx≤1.207 时,5 次谐波补偿才被应用于控制系统中。图A2、A3 中曲线L2与L3分别为调制度Sx与kx、lx的关系曲线,3个参数一一对应。为了便于工程应用,通过5 阶多项式曲线拟合的方式,得到Sx与kx、lx之间的对应关系为:
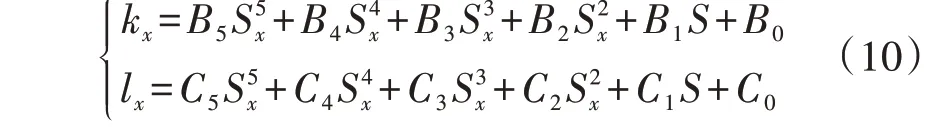
式中:拟合系数B0—B5、C0—C5可由MATLAB 拟合工具箱计算得到,具体见附录A表A1。
4 系统控制框图分析
基于NHCS的CHB 光伏并网逆变器控制框图如附录A 图A4 所示,可实现如下3 个目的:直流侧电压控制;并网电流实现单位功率因数运行;计算各单元的调制波。
4.1 电压环
图A4中,各光伏面板需各自独立运行在其最大功率点处,其最大功率点电压Umpp_x由独立的MPPT算法得到。电压环中,采用n个比例积分控制器,以实现对n个电压进行独立控制。为避免直流母线中二次纹波对电压环控制的影响,将母线电压通过100 Hz陷波器处理[22]后得到udcfx,并将其反馈到系统中;将PI 控制器的输出定义为光伏面板输出电流的给定值,与udcfx相乘后可得到光伏面板功率给定值,进而得到光伏输出总功率给定值P∗T。
4.2 电流环
图A4 中的电流环采用准比例谐振Q-PR(Quasi Proportional Resonance)控制+电网电压前馈解耦的方案。此结构具有算法实现简单、动态响应快、抗干扰能力强等特点[23]。电流环中,首先通过锁相环得到电网电压us的幅值Um及其相角信息ωt;然后,并网电流给定值由除以0.5Um得到;Q-PR 控制器的输出为电感电压给定值,与us相加后可得到时域下总的调制电压给定值。得到后,就可以根据各单元的功率关系得到相应的调制波。
4.3 调制波的计算
由上文分析得,调制波mx由三部分组成,即:
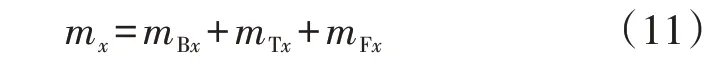
式中:mBx为原始基频调制波;mTx为补偿的3 次调制波;mFx为补偿的5次调制波。
4.3.1 基频调制波计算
由于CHB 采用了级联的形式,并网电流流经所有H 桥单元的交流侧,因此各单元交流侧电压与功率成正比,有:

结合式(12)与式(1),可得到各个单元的原始基频调制波mBx为:
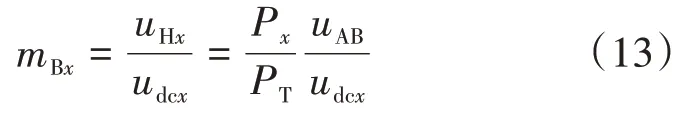
4.3.2 谐波成分计算
只有在各光伏面板功率相差较大,进而导致逆变器某些单元出现过调制的情况下,才会进行谐波补偿来扩宽稳定域运行范围。因此,根据调制度Sx的大小,可分为4 个模式计算不同工况下的谐波成分,如表1 所示。表中:m-Tx、m-Fx分别为反向3、5 次谐波,以抵消谐波补偿对逆变器的影响,使逆变器交流侧电压uAB在谐波补偿后不含3、5 次谐波成分。当然,若系统各单元功率相差不大时,任何单元都不需要补偿谐波,则m-Tx和m-Fx为0。

表1 调制波计算公式Table 1 Formula of modulation wave
假设n个单元中,有i个单元工作在模式2,j个单元工作在模式3,剩余单元工作在模式1,即:1S1,…,Si≤1.155;1.155Si+1,…,Si+j≤1.207;0≤Si+j+1,…,Sn≤1。
模式2 与模式3 都利用了3 次谐波,则系统补偿的3次谐波总量UT为:

只有模式3 利用了5 次谐波,则系统补偿的5 次谐波总量UF为:

非过调制单元的过调制电压裕量Umargin_x定义为:
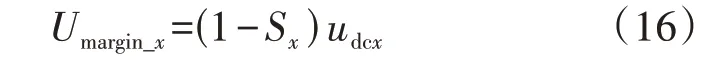
由“能者多劳”原则,各单元过调制电压裕量越大,分配的反向谐波越大,则m-Tx和m-Fx分别表示为:
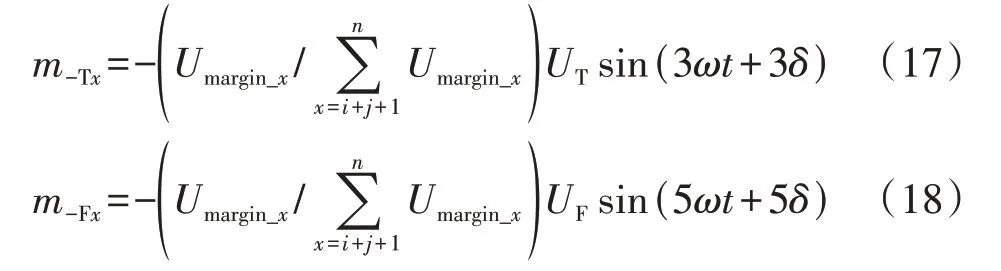
通常情况下,过调制电压总裕量大于所需分配的反向谐波,因此非过调制单元在分配后,调制度仍然会保持在1以下。
5 仿真分析
为验证所提控制策略的可行性,在MATLAB/Simulink 平台上搭建了3 级CHB 光伏并网逆变器的仿真模型,电路具体参数和光伏模块参数分别如附录A表A2、A3所示,每个单元采用3个光伏模块串联。
仿真设置初始时刻3 个单元光伏面板的温度和太阳辐射强度一致,最大输出功率都为600 W,输入平衡;1.5 s 时刻,第1 个和第2 个单元光伏面板太阳辐射强度从1 000 W/m2分别降至417 W/m2和667 W/m2,相应地,最大输出功率分别降至250 W和400 W,第3个单元的最大输出功率保持600 W 不变,输入不平衡。
输入从平衡到不平衡过程中各单元输出功率Pdcx和直流侧电压udcx的控制变化过程分别如附录A图A5 和图A6 所示。由图可见,各单元udcx从开路电压139 V 经MPPT 控制1 s 后达到最大功率点电压121 V,各单元输出功率都稳定在600 W。由于各单元输出功率相等,系统满足稳定运行的前提条件式(7),故各单元不会出现过调制。在这种情况下,系统不需要进行谐波补偿,并网电流is也不会发生畸变,其总谐波畸变率THD(Total Harmonic Distortion)仅为0.45%。在1.5 s 时刻太阳辐射强度突变后,udc1和udc2先下跌再恢复控制到最大功率点电压121 V,相应地,Pdc1和Pdc2也分别稳定到新的最大输出功率250 W和400 W,而第3个单元保持不变。
仿真设置条件下采用传统THCS 的仿真结果如附录A 图A7 所示,1.5 s 后,因第3 个单元的输出功率最大,其调制度S3将大于1,因此需补偿一定量的正向谐波使其调制波m3峰值小于1,相应地,第1 个和第2 个将注入反向的谐波以使交流侧总的电压矢量谐波含量为0。由图A7(a)、(b)可知,由于各单元间功率相差过大,即使补偿系数k3达到1/6,其调制波m3的峰值为1.1,仍大于1,发生了过调制;由图A7(c)、(d)可知,此时并网电流THD 为7.65%,不满足小于5%的并网畸变率要求,逆变器将被离网处理。
图4 为仿真设置条件下采用本文所提NHCS 的仿真结果。由图4(a)、(b)可知,谐波补偿后,第3个单元调制波m3的峰值刚好为1,没有发生过调制;由图4(c)、(d)可知,此时并网电流THD 仅为1.92%,满足5%的并网畸变率要求。
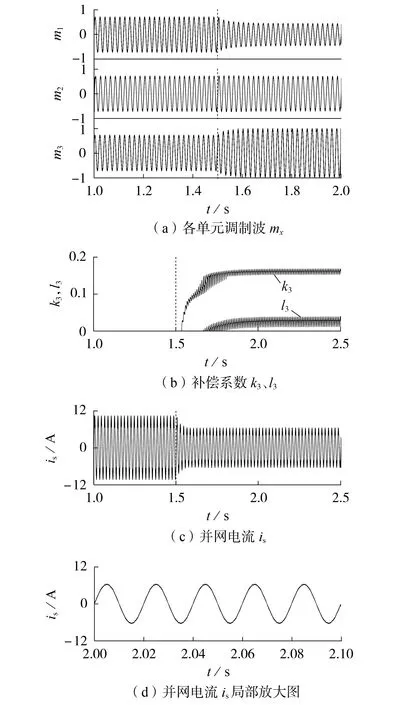
图4 所提NHCS的仿真结果Fig.4 Simulative results of proposed NHCS
由此可见,本文所提NHCS 可以在功率极度不平衡条件下使逆变器工作在稳定运行状态,且相较于传统THCS有更大的稳定域运行范围。
6 实验验证
为了进一步验证所提控制策略的有效性,搭建了3 单元CHB 光伏并网逆变器的实验样机,实验参数如附录A 表A4 所示,实验平台如附录A 图A8 所示。附录A 图A9 为直流电源串联电阻模拟光伏示意图,受实验条件约束,用160 V 直流电源串联电阻(R1//R2)输出来模拟光伏。通过投切R2及将udc控制为145 V 来改变输入功率,观察所提控制策略在功率不平衡下的效果。
6.1 系统在输入功率平衡下的实验结果
图5 为系统在功率平衡下的实验结果。3 个单元的输入功率均稳定在550 W。系统满足稳定运行的前提条件式(7),各单元不会出现过调制。系统不需要进行谐波补偿,并网电流is也不会发生畸变,其THD仅为2.68%。
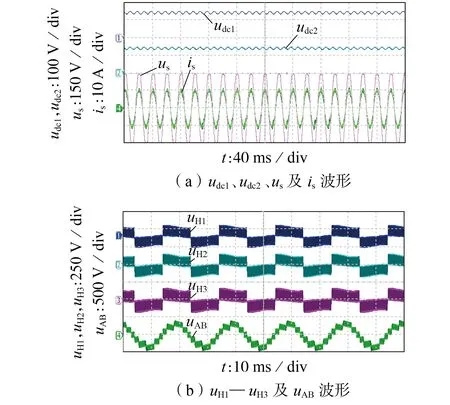
图5 功率平衡下的实验结果Fig.5 Experimental results under power equalization
6.2 系统在输入功率极度不平衡下的实验结果
图6(a)为系统在功率极度不平衡时没有谐波补偿的实验结果。此时第3 个单元不满足稳定运行的前提条件式(7),出现了过调制现象,并网电流THD为41.24%,不满足5%的并网畸变率要求。采用传统THCS得到的实验结果如图6(b)所示,此时第1个和第2 个单元直流侧电压稳定在给定值145 V,并网电流THD 降至9.34%,虽然相比图6(a)的41.24%有大幅下降,但依然不满足5%的并网畸变率要求。

图6 功率极度不平衡下的实验结果Fig.6 Experimental results under extreme power imbalance
图7 为本文所提NHCS 在功率极度不平衡下的实验结果。虚线时刻为输入电阻切换时刻,将第1个单元的等效内阻从3.8 Ω(10.8 Ω 与5.8 Ω 并联)改变为10.8 Ω,第2 个单元的等效内阻从3.8 Ω(6.2 Ω与9.8 Ω 并联)改变为6.2 Ω(断开1 个电阻),第3 个单元的等效内阻不变(保持3.8 Ω),用来模拟光伏面板单元功率突变时刻。功率突变后,第1 个单元直流侧功率PH1由550 W 降至200 W,电流iPV1由3.75 A降至1.38 A,如图7(a)所示;udc1和udc2从145 V 先下跌然后上升恢复到145 V,并网电流由10.67 A 降至7.98 A,THD 为3.96%,如图7(b)所示,这说明控制达到了目标。此阶段第1 个和第2 个单元的输出功率由550 W 分别降至200 W 和350 W,第3 个单元的输出功率保持550 W 不变。图7(c)测试条件与图7(b)相同,除了udc1和is波形,还给出了第1 个光伏面板输出电流iPV1和第2个光伏面板输出电流iPV2波形,反映了控制电流的调节过程。并网电流THD 为3.96%,相较于采用传统THCS 的9.34%,并网畸变率有了明显降低,满足了5%的并网畸变率要求,这证明了所提控制策略的正确性。
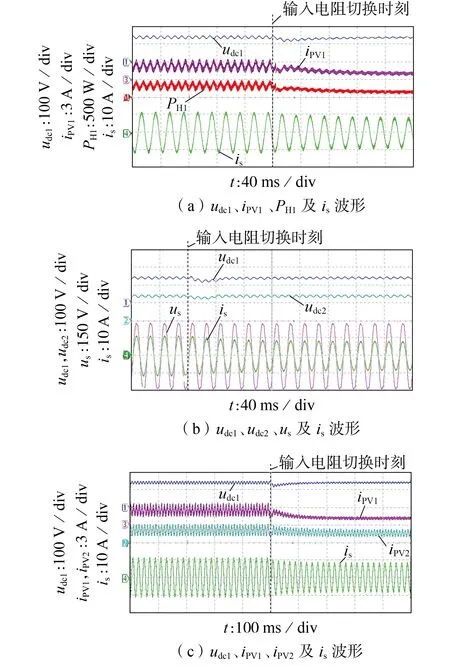
图7 所提NHCS的实验结果Fig.7 Experimental results of proposed NHCS
7 结论
本文基于传统THCS,提出了一种应用于CHB光伏并网逆变器的NHCS,有效提高了CHB 逆变器在功率不平衡下的稳定运行范围,将逆变器过调制能力扩展了33.55%,使得CHB逆变器在输入功率极度不平衡下仍能稳定运行。所提控制策略不增加系统的硬件成本,原理简单且易于实现,便于推广应用。
附录见本刊网络版(http://www.epae.cn)。

