对认证加密算法Pyjamask的伪造攻击*
贺水喻,魏悦川,2,潘 峰,2,畅利鹏
(1.中国人民武装警察部队工程大学密码工程学院,陕西 西安 710086;2.中国人民武装警察部队网络与信息安全重点实验室,陕西 西安 710086)
1 引言
在信息传输过程中,信息的机密性[1]和完整性[2]是保证其安全的2大重要目标。机密性保证信息不被泄露,是抵抗对手被动攻击的一种特性;完整性则防止信息被修改、被篡改,是抵抗对手主动攻击的一种特性。认证加密AE(Authenticated Encryption)算法[3],指能够同时实现消息保密性和完整性的密码算法,并做到同时满足加密和认证功能。在资源受限的环境中,在轻量化和降低资源消耗的同时,对实现数据加密和完整性认证功能的密码保护的需求急剧增长。意识到这一问题,由美国标准技术研究所NIST(National Institute of Standards and Technology)发起了密码竞赛。到目前为止,正在进行轻量级密码LWC(LightWeight Cryptography)标准化[4]。
Pyjamask算法[5]是NIST在全球范围内征集的后量子时代轻量级密码算法之一,入选了LWC竞赛第2轮。该算法设计的目的为在有效抵抗侧信道攻击的同时,以其简单的结构、较少的非线性门数量和适用于并行运算的通用位片结构来大大提高算法效率。目前,关于该算法的安全性分析相对较少,许泽雨[6]给出了Pyjamask-128的自动化分析结果,包括Pyjamask-128的5轮差分分析、6轮飞来飞去(Boomerang)分析和4轮线性分析;Tian等人[7]通过积分攻击得到了Pyjamask-96的11轮区分器;刘亚等人[8]对Pyjamask进行了不可能差分分析,结果显示该算法有很好的抗不可能差分性质。前人从面向位的微观角度对该算法进行了相关分析,而相对于原始的操作模式,本文发现可以从结构性质上进行明文伪造,依概率达到伪造成功的效果。
伪造攻击[9]的基本思想是通过伪造不同的明文或密文分组从而产生与合法密文解密相同的认证标签,达到通过认证的目的。对于合法密文而言,该操作破坏了密文的完整性。本文对Pyjamask算法的结构进行分析时发现,该算法与入围CAESAR(Competition for Authenticated Encryption: Security, Applicability and Robustness)竞赛[10]第2轮的SCREAM算法[11]结构十分相似。结合田玉丹等人[12]对SCREAM算法利用累加值碰撞的思想提出的新伪造攻击方法,本文实现了对Pyjamask算法的删除明文伪造。在保持明文的异或值sum不变的情况下,本文通过选择明文[13]进行伪造,且成功通过了验证,从而达到对Pyjamask算法的选择明文伪造攻击。
2 Pyjamask算法描述
Pyjamask算法的基本模块采用了SPN(Substitution-Permutation Network)结构,算法包含2种分组长度:96比特和128比特,分别对应Pyjamask-96和Pyjamask-128。加密过程为(C,tag)=EK(N,A,M),K表示密钥,输入可变长的明文M、可变长的相关数据A和定长的公共消息N,输出密文C和标签tag。解密过程为M=DK(N,A,C,tag),输出对应明文M和验证标签tag*(判断tag=tag*是否成立,若相等则返回明文M,否则返回空)。Pyjamask算法的加密过程共分为相关数据处理、明文加密和tag生成3个部分。
2.1 相关数据处理
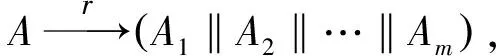
Si=Si-1⊕EK(Ai⊕Oi)
(1)
式(2)为最后分组长度为r比特和不足r比特时auth的值计算方式:
(2)
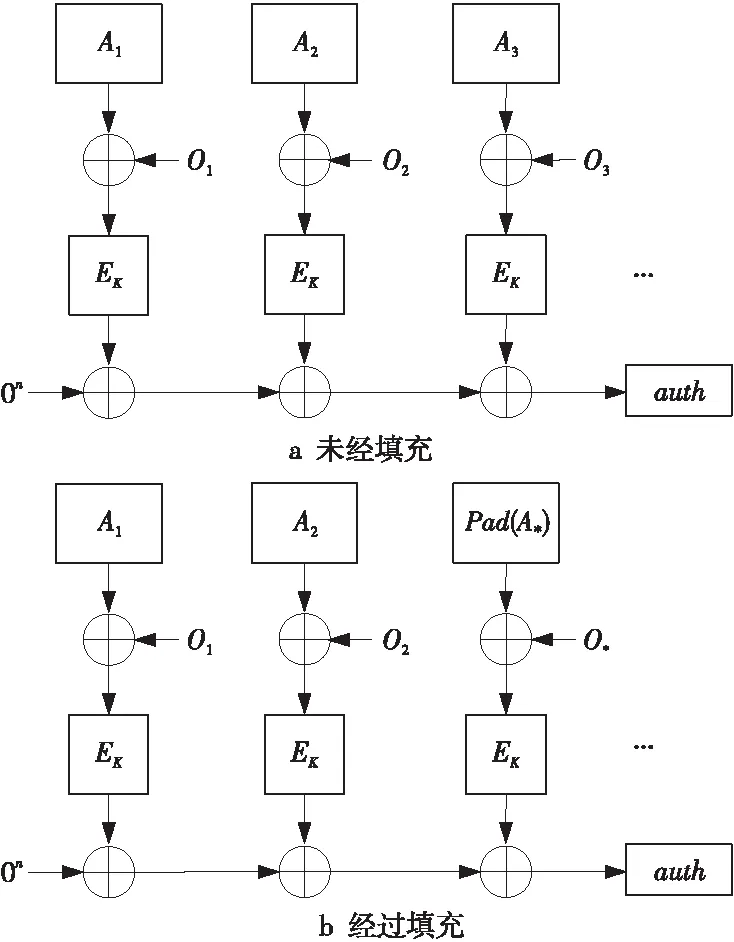
Figure 1 Processing processes of related data
2.2 明文加密
明文加密部分的输入为密钥K、公共消息N、相关数据A和明文M,输出为密文C及产生的中间值sum,如图2所示。与相关数据处理几乎一致,将明文M分成m组,即M=M1‖M2‖…‖Mm。但是,在通过加密模块EK前后都与Oi进行异或得到密文C,即C=C1‖C2‖…‖Cm。若最后明文分组长度不足r比特,生成密文的方式如式(3)所示:
Pad=EK(O*)
C*=M*⊕Pad[1…|M*|]
(3)
其中,Pad表示计算的中间量,Pad[1…|M*|]取Pad的后半段与M*运算。sum值的计算方式为sum=M1⊕M2⊕…⊕Mm,相应地,当明文最后一个分组长度不足r比特时:sum*=summ-1⊕(M*‖1‖0127-|M*|)。
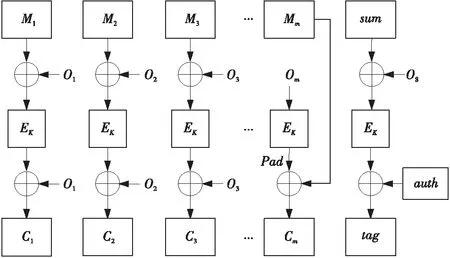
Figure 2 Encryption process of Pyjamask
2.3 tag生成
标签tag生成部分(见图2)是利用前2部分得到的auth和sum来生成最后的tag值,具体计算过程如式(4)和式(5)所示:
auth=HASH(K,A),
O$=Om⊕L$,
tag=EK(summ⊕O$)⊕HASH(K,A)
(4)
O$=O*⊕L$,
tag=EK(sum*⊕O$)⊕HASH(K,A)
(5)
其中,O$等参数的计算方法是通过有限域dbl运算产生的,式(4)和式(5)分别表示明文未填充和经过填充时tag值的计算过程。调整参数Oi的计算过程相对独立,通过式(6)和式(7)计算产生:
(6)
Oi=Oi-1⊕Lntz(i)
(7)
其中,ntz(x)函数表示将x转化为二进制后,用所包含0的个数代替x;dbl(x)表示使用有限域字段中倍加操作,具体如式(8)所示:
(8)
3 Pyjamask算法的伪造攻击
3.1 Pyjamask算法的删除明文伪造攻击
由第2节对Pyjamask算法的介绍可知,可将明文划分为m个分组,即M=M1‖M2‖…‖Mm-1‖Mm(本文默认最后一个明文分组是经过填充的),在加密明文的过程中对应分组使用参数Om,第m分组使用O*。根据该特性可以进行如下过程的攻击:
Step1分别对明文分组Mi进行加密,加密过程如图2所示。设公共消息为N,相关数据为A,输入明文为M,其中存在分组Mm-r⊕Mm-r+1⊕…⊕Mm-3⊕Mm-2=0(共r-1个分组,2≤r≤m),输出密文C=C1‖C2‖…‖Cm-1‖Cm和标签tag。
Step2保持Step 1中的N和A不变,伪造m-r组明文M′=M1‖M2‖…‖Mm-r-1‖Mm-r(其中Mm-r+1⊕Mm-r+2⊕…⊕Mm-1⊕Mm=0,故删去这r个明文分组),加密过程如图3所示。输出值为(C′,tag′),其中C′=C1‖C2‖…‖Cm-r-1‖C*。

Figure 3 Encryption process of m-r plaintext group
伪造攻击的有效性分析:在2次加密过程中使用相同相关数据A的条件下,如图1中对相关数据处理时的auth值是相同的。Step 1中加密明文M=M1‖M2‖…‖Mm-r-1‖Mm-r‖…‖Mm-2‖Mm-1‖Mm有Mm-r+1⊕Mm-r+2⊕…⊕Mm-1⊕Mm=0,因此2次加密的sum存在以下关系:
∑M=∑M′⊕Mm-r+1⊕Mm-r+2⊕…⊕
Mm-1⊕Mm=∑M′
即Step 1和Step 2加密过程得到的累加值sum是相同的。又因为2次保持加密过程中的公共消息N相同,且最后一个明文分组都是Mm,由文献[6]知,加密过程中使用的参数O$仅与最后一个明文分组加密使用的参数Om相关,并且各参数与对应的明文分组相对独立。根据以上3个条件和tag的生成方式可知:tag′=tag,即2次加密得到的认证标签相同,验证通过。根据图3的加密过程,攻击者可以成功获得加密的密文,实现信息伪造,并且成功的概率为1。
3.2 Pyjamask算法的选择明文伪造攻击
针对Pyjamask算法类OBC(Operational Cipher Block)模式的结构特性,攻击者又可以通过在明文中引入差分对Δ⊕Δ′=0,使得2次加密时伪造的明文分组与原始明文分组计算所得的sum值相等,达到了高概率地引入差分对伪造攻击的目的。攻击者可以利用s+1组明文,即分别使用1组或多组明文进行加密。根据明文分组异或得到sum这一特性,则2次加密可以产生相同的认证标签,即tag′=tag,并且通过验证达到成功伪造的效果。
3.2.1s=0时的伪造攻击
当s=0时,攻击者只掌握1组明文M=M1‖M2‖…‖Mm-1‖Mm。通过引入差分对构造1组明文M′=M1‖…‖M′j‖…‖M′k‖…‖Mm-1‖Mm分组(在分组M′j和M′k中引入差分对),如图4所示,加密后产生的新标签与使用原始明文加密得到的标签一致,验证通过。
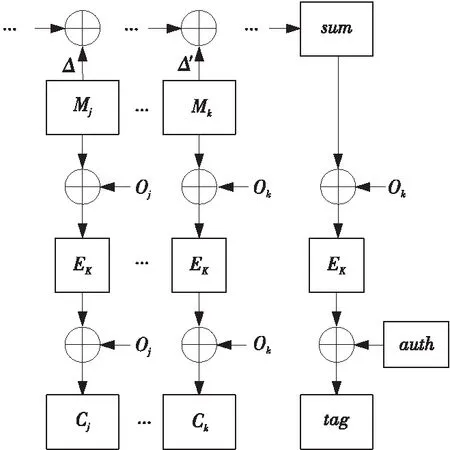
Figure 4 Encryption process with differential pair
攻击过程如下所示:
Step1选定公共消息N和相关数据A进行处理,对已知的明文分组M=M1‖M2‖…‖Mm-1‖Mm进行加密操作,得到中间值auth和明文的异或和sum,输出(C,tag)。
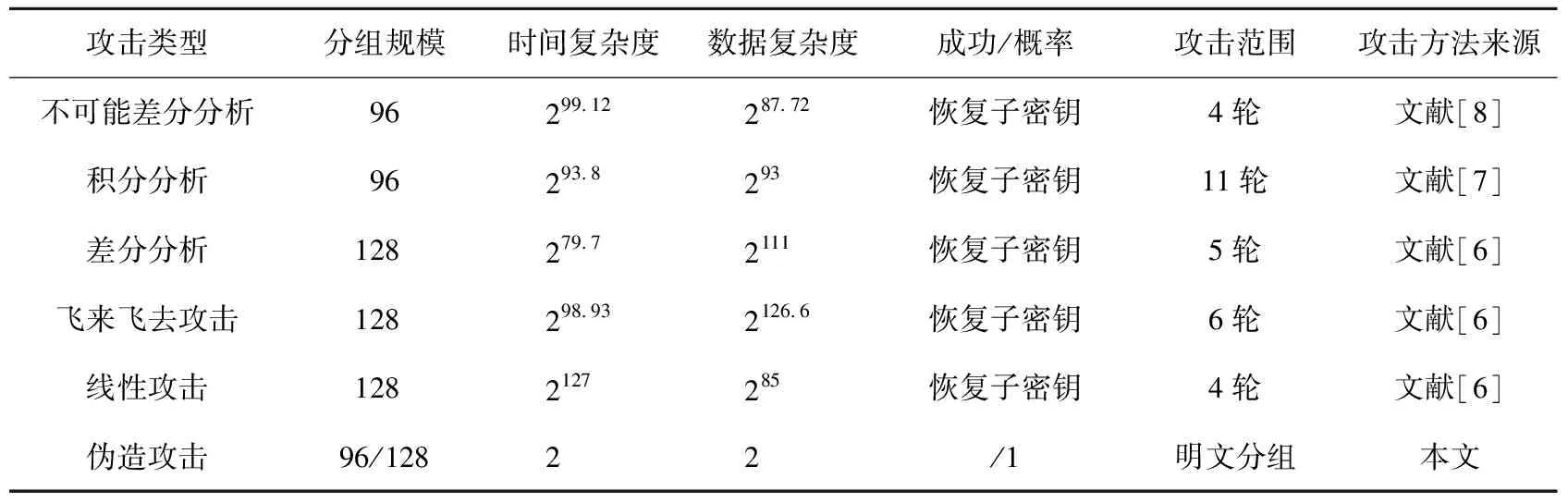
Step2保持Step 1中的N和A不变。攻击者通过给已知的明文M=M1‖M2‖…‖Mm-1‖Mm分组中注入差分对得到新的明文分组M′=M1‖…‖M′j‖…‖M′k‖…‖Mm-1‖Mm(1≤j 有效性分析:相关数据A依然保持不变,2次处理得到的auth值相同。在s=0时,引入差分对Δ⊕Δ′=0,伪造的明文中除M′j和M′k外,其它分组与已知明文M=M1‖M2‖…‖Mm-1‖Mm保持相同,加密过程得到的sum值相等,即: 因此,2组明文加密产生的认证标签tag一致,伪造后的明文加密后得到密文C′=C1‖…‖C′j‖…‖C′k‖…‖Cm-1‖Cm,得证以概率1成功伪造。 Table 1 Comparison of analysis results of Pyjamask 在实际操作过程中(如图3和图4所示),攻击者可以选用删除明文和引入差分对实施伪造,并且伪造成功的概率为1,消耗的时间和数据复杂度为2,较为高效。通过累加遍历多组明文,得到包含差分对的明文分组,以此进行伪造时消耗的数据量较大,但成功伪造的概率仍然为1。表1列出了Pyjamask算法的现有分析结果,文献中的分析方法所对应的时间复杂度和数据复杂度均较高,因此本文提出的攻击方法更加实用有效。 认证加密算法的方案设计与安全性分析是当前密码学方向的研究重点及难点。本文基于Pyjamask算法的结构和参数特点,提出了2种伪造方案,通过构造明文,产生局部碰撞的方式,找到了与原始明密文产生相同tag的明密文对应关系,成功实现了认证标签的伪造。对于删除明文的伪造,成功的概率为1,攻击的时间复杂度和数据复杂度可以忽略不记,操作方式更加简便有效。对于选择明文的伪造,当攻击者知道1组分组时,通过引入差分对,加密时产生碰撞,此时伪造成功的概率仍然为1,适用性良好;当已知s+1组明文时,攻击者通过已知的明文信息,获取可产生碰撞的明文分组,并且将获得的可碰撞明文分组引入预留的1组明文当中,产生伪造,成功的概率也为1。本文在实际操作的过程中发现,相对于前2次攻击,通过遍历获取可碰撞分组对数据的要求较高。3.2.2 s>0时的伪造攻击

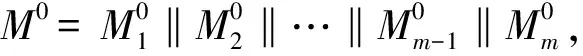

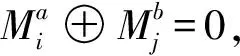

4 结果对比与分析
5 结束语

