故障检测率对软件可靠性影响实证分析*
孙智超,张 策,江文倩,刘凯卫,范苗苗,李文毓,温雅菲
(1.哈尔滨工业大学(威海)计算机科学与技术学院,山东 威海 264209;2.华为技术有限公司南京研究所,江苏 南京 210012)
1 引言
随着信息技术与网络的发展,计算机的应用也越来越广泛。计算机软件作为用户使用计算机的主要载体与功能提供者,在生产生活中具有重要作用。人类对软件功能的要求不断增加,软件的规模与复杂度也在不断增加,软件质量管理在软件开发与测试中愈加重要。软件可靠性是软件质量评估的重要因素,高质量的软件必然是高可靠的。软件可靠性增长模型SRGM(Software Reliability Growth Model)是软件可靠性研究的主流方法之一。在一般的SRGM模型中,有2大重要参数[1],一是软件总故障,它对软件系统中整体故障数量进行了抽象;二是故障检测率FDR(Fault Detection Rate),它描述了软件测试环境的测试能力。为了更好地掌握软件可靠性,以达到预期(发布)要求,需要分析故障检测率在可靠性研究中的作用。
故障检测率FDR刻画了测试环境、测试技术、测试资源消耗情况及测试人员技能的综合能力[2]。客观上测试环境的不同,以及测试人员实施测试策略的差异,都会使不同软件系统在测试中表现出不同的外在特征。从建立数学模型的角度来看,不同模型的区别与故障检测率FDR关联紧密。这样,故障检测率FDR从整体上刻画了测试效果,使其成为影响SRGM性能的主要评测点,对软件可靠性建模、软件故障数量预测、最优发布时间的确定和测试成本的控制等工作具有重要意义。
近些年,软件可靠性增长模型的研究重点主要集中于软件可靠性模型[2,3]、模型参数估计方法[4]和确定软件发布时间[5]等方面,而对于已有模型的研究不够深入,特别是SRGM的2大重要参数对模型性能的影响分析。本文主要从故障检测率出发,在失效数据集FDS(Failure Date Set)上建立统一的模型,提出2种评测机制:单SRGM单FDS多FDR模式和多SRGM多FDS多FDR模式。通过多属性决策的评测算法,分析可靠性模型、失效数据集FDS与故障检测率FDR三者之间的关联。基于实验结果分析故障检测率对于SRGM的影响。
本文结构组织如下:第2节回顾了目前已有的故障检测率函数;第3节阐述了SRGM的建模方法,包括基本假设、建模方法与具体计算方法等;第4节基于2个方案分析了不同故障检测率函数对SRGM模型的扰动影响;最后对全文进行总结。
2 故障检测率回顾
故障检测率表示单位时间内单个故障被检测到的平均概率[6],通常用b(t)表示。Goel与Okumoto[7]提出了最早的SRGM模型——G-O模型。在此模型中,故障检测率被认为是常量型的,即b(t)=b,并不能反映出随着测试时间的增加,测试人员熟练程度的变化,具有明显的缺陷。Yamada等[8]提出了S型增长趋势的故障检测率函数——延迟SRGM模型和变动SRGM模型,具有更强的适应能力,灵活性更高,模型性能预测效果更好。Yamada等[9]提出了考虑测试工作量的软件可靠性增长模型,所提模型具有良好的性能。Huang等[10]提出了一个考虑学习因子的故障检测率模型,并完成了相关SRGM模型推导工作。Pham[11]提出了一个Vtub型的故障检测率函数,在测试初期考虑了软件刚加入测试,故障检测率较高,随着测试时间的增加,故障检测率逐渐降低并趋于稳定,在测试工作的末期,随着上线日期的临近,故障检测率又呈现出升高的趋势。Song等[12]提出了基于操作环境不确定性的广义模型,其核心是在故障检测率函数中增加了体现环境变动的随机变量,一般为伽玛分布。此外,Pham等[13]提出了一个具有随机性的通用故障检测率模型,并考虑了加性高斯白噪声与静态乘性噪声2种不同情况。
本文遴选了6个广泛应用的故障检测率函数,并分析了这些故障检测率函数对于SRGM的影响。如表1所示,这6个故障检测率可划分为4种类型:常量类型、幂函数类型、S型和指数型。
3 FDR对软件可靠性影响的建模
3.1 基本框架
首先,给出SRGM建模的公共假设:
(1)软件失效满足非齐次泊松过程NHPP(Non-Homogeneous Poisson Process)过程[14];

Table 1 Type of fault detection rate
(2)在(t+Δt)内检测到的故障数量与当前软件中剩余的故障数量成比例;
(3)软件修复过程中存在排错不完全和新故障引入的现象[15]。
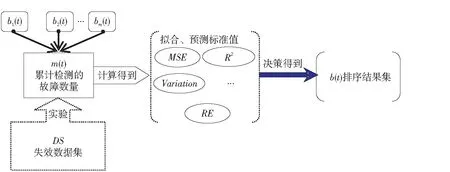
Figure 1 Evaluation and decision-making process of b(t)in solution 1
本文将在以上假设的基础上建立不同故障检测率对应的SRGM模型,基本的微分方程形式如式(1)所示:
(1)
其中,m(t)为累计故障检测函数,其值表示软件测试中0~t时间段内已被检测出的故障数量;b(t)是故障检测率函数,其值在(0,1);a(t)表示软件总故障数量,可设定为常量,或测试时间t的某种函数;p是故障修复概率,其值在(0,1)。将不同形式的a(t)、b(t)和变量p带入微分方程即可求解出对应的m(t)。
本文将从以下3步出发,逐步确定FDR、SRGM和FDS:
第1步基于我们前期的研究成果和大量的实验,遴选出在预定FDS上具有优秀性能的SRGM集合。这些SRGM集合包括第2节中的从FDR视角建立的可靠性模型;
第2步建立待观测的FDR集合。此集合虽不能由前期实验得出,但可选择当前研究中出现频率较高的FDR;
第3步建立评测FDR及其对SRGM可能产生影响的观测点集合。
由于每种失效数据集FDS都对应着特定的软件测试环境,同时SRGM的基本假设可以分为考虑完美排错或不完美排错,本文考虑到在单一与众多测试环境下、不同SRGM假设情况下的故障检测率对于SRGM模型的不同影响,提出了2个方案进行实证分析,以全面地探究故障检测率对SRGM性能的影响。方案1考虑了单一测试环境、完美排错的SRGM模型中故障检测率FDR对于SRGM模型的影响。方案2考虑了多测试环境、不同排错假设中故障检测率FDR对SRGM模型的影响。
3.1.1 方案1——单SRGM单FDS多FDR模式
在完美排错的假设的基础上,改变式(1)中的b(t)函数,便可得到不同故障检测率FDR对应的累计故障检测函数m(t)。在单一失效数据集上分析不同m(t)的拟合性能与预测性能,即对应不同故障检测率对应的SRGM模型的性能。由此进行分析,便可得到固定测试环境下的故障检测率FDR对软件可靠性增长模型的影响。这种方案被称为单SRGM单FDS多FDR模式。通过观测得到的拟合与预测数值,并经过适当的决策算法可给出FDR排序结果(即偏序集合)。图1和算法1分别描述了此方案的基本流程和相应的执行算法EvaluateFDREffectOnSRGM—SSSFMF,其中m表示参与对比的故障检测率函数的数量。算法1中SortFDR()实现对模型的排序,排序的基本算法为基于优劣解距离法TOPSIS(Technique for Order Preference by Similarity to Ideal Solution)[16]的SRGM决策算法,详见3.2节。
算法1方案1的执行算法EvaluateFDREffectOnSRGM—SSSFMF
输入:(通过大量实验)遴选出的SRGM模型m(t)、失效数据集DS、故障检测率集合FDRSet=[bt1,bt2,…,btm]。
输出:FDR偏序集合FDRSet。
Step1遍历故障检测率函数,计算对应的累计故障检测函数m(t),并计算失效数据集上m(t)的拟合预测性能:
i=0;
Foreachbi(t)in(FDRSet){
MT[i]=Fitting(m(t),DS,bi(t));
MSE[i]=CalculateMSE(MT[i]);
R_square[i]=CalculateR_square(MT[i]);
Variation[i]=CalculateVariation(MT[i]);
RE[i]=CalculateRE(MT[i]);
i++;
}
Step2通过信息熵计算每个性能指标的权重:
W=CalculateWeight(MT,MSE,R_square,Variation,RE);
Step3得到经决策算法处理后的FDR偏序集合:
FDRSet=SortFDR(MT,MSE,R_square,Variation,RE,W);
Step4returnFDRSet
在这种单SRGM单FDS多FDR模式中,由于是基于单个的SRGM和失效数据集FDS来进行研究,因而其被限定在某个特定的软件测试环境下。基于该分析结果便于改进测试策略,使得其故障检测率能够向着符合测试要求的方向改进。
3.1.2 方案2——多SRGM多FDS多FDR模式
为了更广泛地分析故障检测率对软件可靠性的影响,方案2考虑了基于完美排错与不完美排错假设的SRGM模型,并在多个失效数据集FDS上进行实证分析。这种情况被称为多SRGM多FDS多FDR模式。
在方案1基础上,将遴选出的多个SRGM和多个FDS分为若干个组,在每一组内将不同的FDR代入到式(1)中,求解出对应的SRGM模型,并在失效数据集上进行实验。通过观测实验的拟合与预测指标,可对SRGM模型进行排序,进而得到不同形式的FDR的性能综合指标。对每一组均进行上述实验,得到了多组不同FDR的性能综合指标。最后经过适当的决策算法可给出全部FDR的排序结果(即偏序集合)。图2和算法2分别描述了此方案的基本流程和相应的执行算法EvaluateFDREffectOnSRGM—MSMFMF,其中n表示SRGM模型的数量。算法2中SortFDR()实现对模型的排序,排序基本算法为基于TOPSIS的SRGM决策算法,详见3.2节。
算法2方案2的执行算法EvaluateFDREffectOnSRGM—MSMFMF
输入:(通过大量实验)遴选出的SRGM 模型集合SRGMSet和失效数据集集合DSSet、故障检测率集合FDRSet=[bt1,bt2,…,btm]、SRGM权重W1、失效数据集权重W2。
输出:FDR偏序集合FDRSet。
Step1计算每个组中针对每个不同SRGM的FDR单一性能值:
i=0,j=0;
Foreachbi(t)inFDRSet{
Foreachmj(t)inSRGMSet{
MT[j]=Fitting(mj(t),DSSet[j],bi(t));
MSE[j]=CalculateMSE(MT[j])
R_square[j]=CalculateR_square(MT[j]);
Variation[j]=CalculateVariation(MT[j]);
RE[j]=CalculateRE(MT[j]);
FDRSingleValue[j]=GetFDR(MT[j],MSE[j],R_square[j],Variation[j],RE[j],W);
j++;
}
FDRItegraedValue[i]=GetFullFDR(FDRSingleValue);
i++;
}
Step2通过信息熵计算每个性能指标的权重:
W=CalculateWeight(MT,MSE,R_square,Variation,RE);
Step3得到经决策算法处理后的FDR偏序集合:
FDRSet=SortFDR(FDRIntegratedValue,W,W1,W2);
Step4returnFDRSet
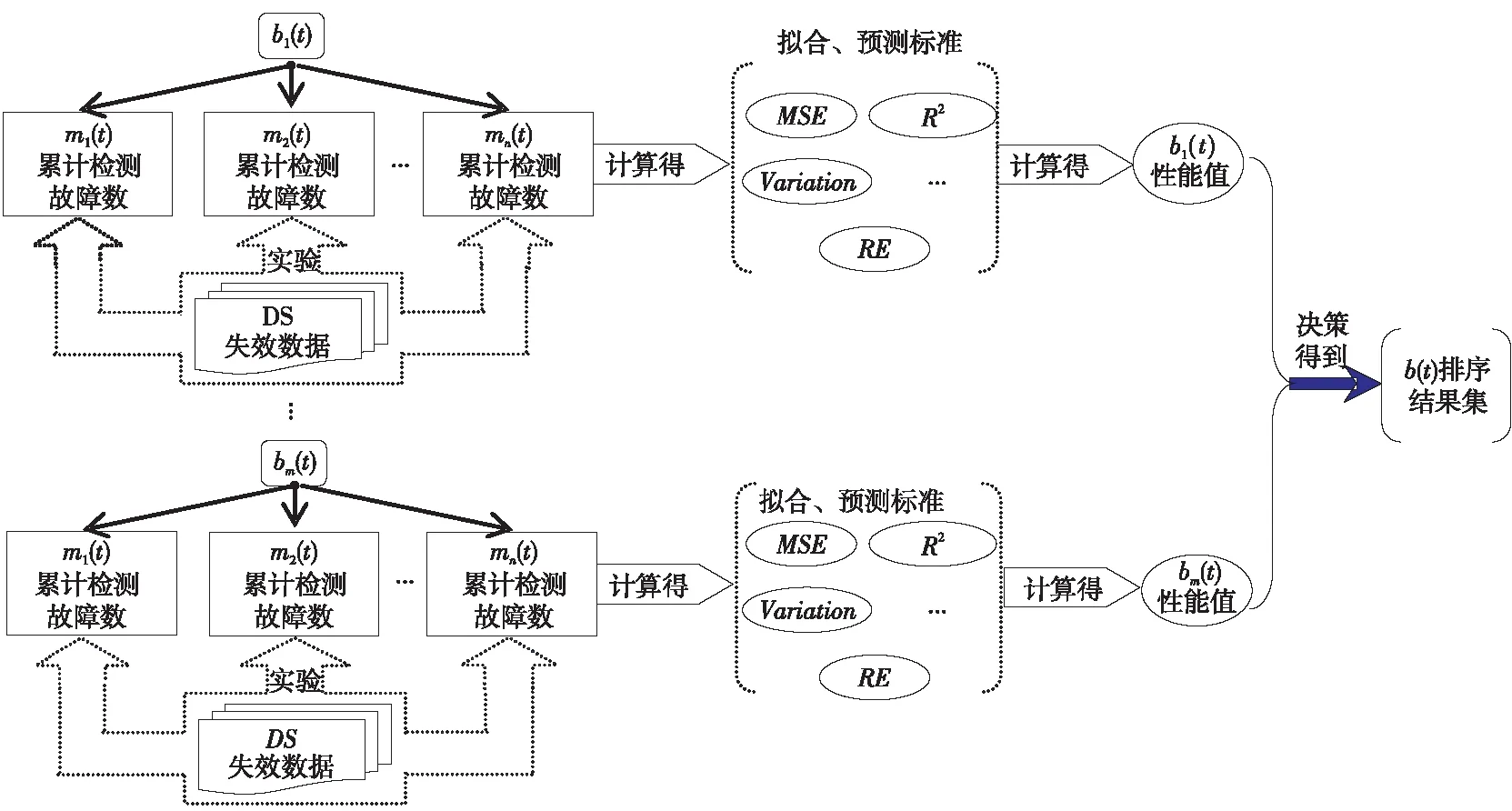
Figure 2 Evaluation and decision-making process of b(t)in solution 2
在这种多SRGM多FDS多FDR模式中,由于是基于多个SRGM和多个失效数据集FDS来进行研究,并没有被限定在某个特定的软件测试环境下,这样可以用于综合分析不同FDR的真实性能,对软件测试过程中的共性情况进行分析,从而得到对于软件测试开发具有重要价值的结论来指导实际软件测试过程。
3.1.3 拟合与预测指标选择


Table 2 Fitting indices
预测指标RE主要通过观测预测曲线形状与RE曲线最后5个值的绝对值平均数综合考量,借助层次分析法AHP(Analytic Hierarchy Process)将预测实验结果进行量化,最终转化为定量的性能指标。RE指标量化值如表3所示,共分为5级。最终RE指标为标准化后的量化级别。

Table 3 Quantified level of RE indicator
3.2 基于TOPSIS的SRGM决策算法
根据SRGM模型在失效数据集上的拟合预测指标对模型进行排序,这是一个多准则决策问题。其中各指标权重采用信息熵的方式计算确定,具体的决策算法为基于优劣解距离法TOPSIS算法[16]。采用信息熵+TOPSIS对所选模型进行排序,得出综合性能最优的SRGM,进而分析故障检测率对软件可靠性的影响。
n个SRGMs在指定数据集上的m个拟合与预测值排列组合成多属性决策矩阵MADM(Mutltiple Attribute Decision Matrix)的形式,如式(2)所示。
(2)
3.2.1 基于信息熵计算权重
对MADM每一列正则化得式(3):
(3)

随后根据正则化矩阵计算每一个指标的信息熵,如式(4)所示:
(4)
其中,Ei为第i个指标的信息熵,E0为信息熵常量,值为(lnm)-1。
根据式(5)计算每一个指标的发散度:
Di=1-Ei
(5)
根据式(6)计算每一个指标的信息熵权重:
(6)
3.2.2 基于TOPSIS进行决策
在决策矩阵MADM的基础上,选出每一列的最大值r(n)与最小值r(1)构成SRGM的正向最优解与负向最劣解,得到的最优最劣决策矩阵PNDM(Positive Negative Decision Matrix)形式如式(7)所示:
(7)
为了消除不同指标值的量纲的影响,将矩阵按照式(8)的形式标准化:
(8)
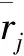
标准化之后的矩阵如式(9)所示:
(9)
再对每一列乘以3.2.1节中计算出的每一个性能指标对应的权重,得到加权最优最劣决策矩阵WPNDM(Weighted Positive Negative Decision Matrix),如式(10)所示:
WPNDMstd=
(10)
随后计算第i个模型SRGMi的性能指标(qi1,qi2,…,qim)到正向最优解集合(q(n)1,q(n)2,…,q(n)m)和负向最劣解集合(q(1)1,q(1)2,…,q(1)m)的距离,进而计算接近程度Hi,确定最终SRGMs偏序顺序。

(11)

(12)
则第i个模型SRGMi与理想解的接近程度Hi可通过式(13)计算:
(13)
对n个SRGMs的接近程度Hi进行排序,即可得到SRGM在该数据集上的偏序集合[H(1),H(2),…,H(n)],其中H(n)对应的SRGM即为在该数据集上性能最佳的模型,H(1)对应的模型即为该数据集上性能最差的模型。随即可根据排序结果分析不同FDR函数对SRGM性能的影响。
TOPSIS决策算法相较于经典的多属性决策算法(加权平均法与熵值法),既考虑了备选解中的最优解应尽可能地靠近理论最优解,又考虑了备选最优解应尽可能地远离理论最劣解。相较于仅考虑每一个备选解指标的简单加权算法与熵值法,TOPSIS决策算法对于SRGM模型排序这种复杂多属性决策问题有更好的决策结果。
4 实验与分析
4.1 实验设置
本节主要介绍实证分析中涉及的SRGM类型、SRGM模型表达式与失效数据集等信息。
4.1.1 SRGM模型
对于方案1(单SRGM单FDS多FDR模式),本文选用完美排错模型,假设软件总故障数量为固定常数,即a(t)=a,故障修复概率固定为1,即p=1,SRGM模型的表达式见表4。表中给出了完美假设下不同b(t)函数对应的SRGM模型,随后在公开发表的失效数据集上进行拟合与预测,观测不同FDR对于SRGM模型的影响。

Table 4 Models compared in solution 1
对于方案2(多SRGM多FDS多FDR模式),选择了如表3所示的软件可靠性增长模型,其中选择2类SRGM模型,分别为完美排错与不完美排错。完美排错的基本假设与方案1所选择模型相同;对于不完美排错SRGM模型,本文选取在之前的研究中性能表现较好的软件总故障模型——折中类型a(t)。为了简便计算,取故障修复概率p(t)=p,参与比较的各模型的表达式见表5。

Table 5 Models compared in solution 2
表5展示了不同b(t)在不完美与完美排错2种假设下对应的SRGM模型表达式,随后将在5个真实失效数据集上对SRGM模型进行拟合,并计算出拟合性能与预测性能,以分析不同SRGM模型、在不同数据集上FDR对SRGM性能的综合影响。
4.1.2 失效数据集
失效数据集FDS是评估SRGM模型的性能、分析故障检测率对SRGM模型影响的基础。本文将会使用5个失效数据集进行相关实验:(1)AT&T Bell实验室的网络管理系统[17],记为DS1;(2)某大型医疗记录系统[18],记为DS2;(3)数组定义语言解释器Space[19],记为DS3;(4)Eclipse开放源码软件系统[20],记为DS4;(5)Apache开源项目ActiveMQ软件系统,记为DS5;(6)PL/I数据库应用[21],记为DS6。
第1个数据集DS1记录了AT&T Bell实验室开发的网络管理系统的故障数量,在680.02个CPU单位时间内累计记录了22个软件故障。第2个数据集DS2记录了某大型医疗系统3个版本的故障信息。该系统由188个组件构成,在18周的记录中,累计发现176个故障。第3个数据集DS3来自于Space程序,包括9 564行C语言代码。在观测的403个CPU单位时间内,共发现21个故障。第4个数据集DS4记录了开源项目Eclipse自2001年10月10日至2013年12月17日期间遇到的所有故障数量,共计6 495个。第5个数据集DS5选取了ActiveMQ软件系统自2020年4月18日起87周的累积检测故障数量(包括正式版与测试版),共计345个故障。第6个数据集DS6是一个由大约317 000行代码组成的PL/I数据库应用软件系统的数据。在19周内,消耗了47.65个CPU单位时间,删除了328个软件故障。图3展示了本文所选数据集的增长曲线。从图3中可以发现,失效数据集的增长趋势为指数型增长(DS1与DS3等)与S型增长(DS2),其中指数型增长也可以划分为数学曲线上的凸型指数增长(DS1)与凹型指数增长(DS3)。
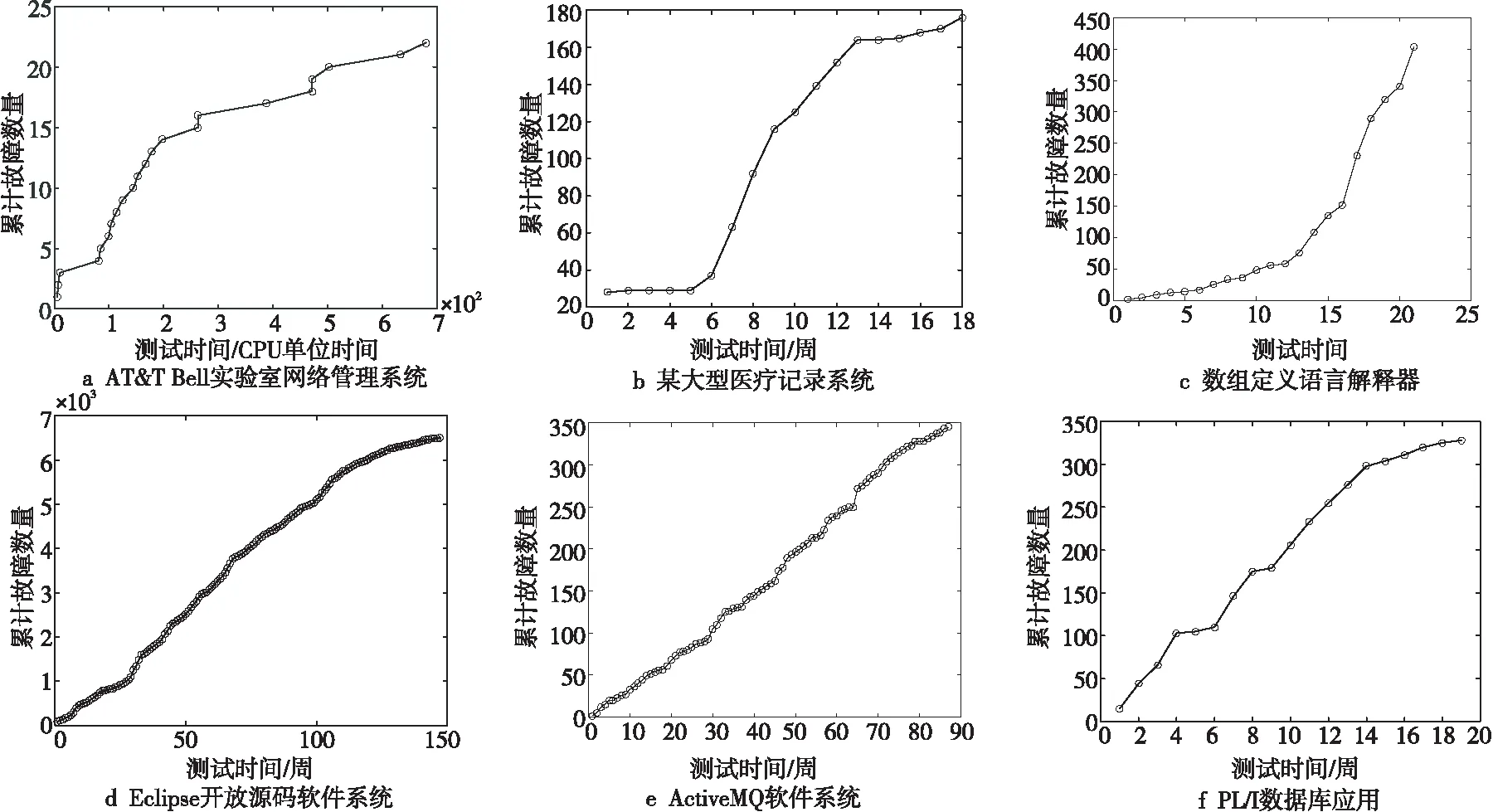
Figure 3 Growth curve of failure data set
4.2 实验结果与简要分析
4.2.1 方案1实验分析
本节主要分析单SRGM单FDS多FDR模式在真实失效数据集上基于TOPSIS决策算法得出的偏序序列。在失效数据集DS6上对方案1进行分析,基于参数估计、拟合性能计算与预测性能计算,得到方案1的初始多属性决策矩阵MADM1与各性能指标对应权重如表6所示。从表6可以看出在对应数据集上,预测性能RE指标的信息熵权重最大,3个拟合指标中MSE信息熵权重最大,R2与Variation对应权重近似一致。所有拟合指标权重和为0.571,略大于预测性能指标权重。
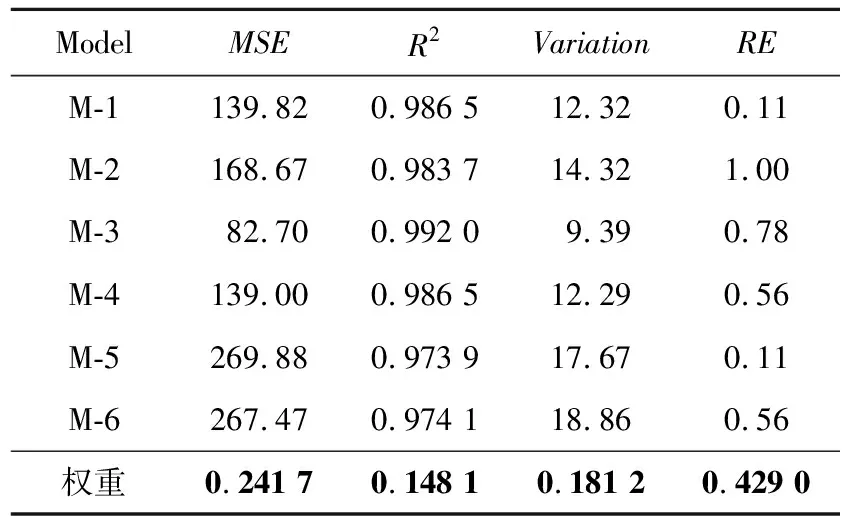
Table 6 Performance indicators and corresponding weights
经计算,方案1中模型(M-1~M-6)与理想解的接近程度如表7所示,分析结果可以发现,在完美排错测试环境中,对于所选数据集DS6,幂函数型b2(t)对应的M-2模型性能最好,S型b3(t)对应的M-3与指数型b6(t)对应的M-6性能较好,常数型b1(t)对应的M-1模型性能最差。
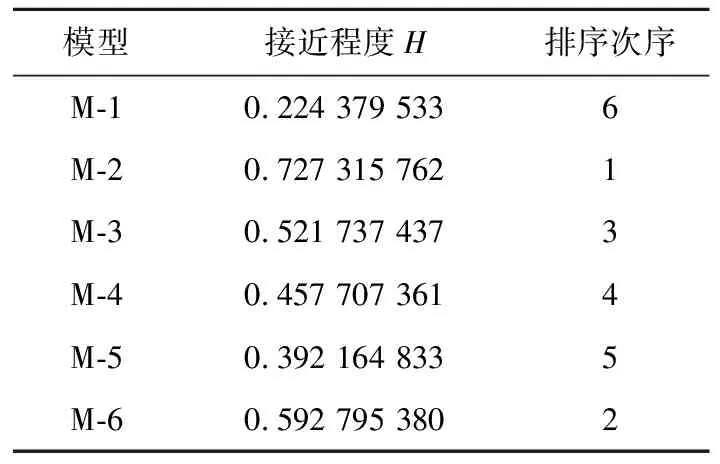
Table 7 Proximity of the models in solution 1
幂函数型b2(t)描述了随着测试时间增加,测试人员对于故障的检测能力不断增强,这符合凸型指数型曲线的增长趋势,故其对应的模型M-2性能最出色。复杂指数型b5(t)反映了随着测试时间增加,故障检测率不断递减,这与数据集的增长趋势相反,故其对应的模型M-5性能较差。常量型b1(t)描述了故障测试率不变的情况下,其对应的模型M-1缺少灵活性,故其性能表现最差。
4.2.2 方案2实验分析
为了进一步分析不同FDR的真实性能,本节遴选了5个真实失效数据集DS1、DS2、DS3、DS4和DS5。DS1具有凸型指数增长趋势,DS2具有S型增长趋势,DS3具有凹型指数增长趋势,这3个数据集均来源于软件可靠性研究中早期经典数据集;DS4与DS5来自于开源软件平台,其数据集的更新时间较新、数据集规模更大。将表5中模型(M-1~M-12)在这5个数据集上进行拟合性能与预测性能分析(由于页面限制,可联系作者获取具体拟合预测指标数据)。
对实验数据集上的性能指标权重进行观测可知,权重的大小主要由各模型在不同数据集上性能指标的差异决定,模型间的指标值差距越大,混乱程度越高,信息熵权重越大。反之,差距越小,则信息熵权重越小,例如R2指标。
表8展示了经由 TOPSIS算法排序后的模型接近程度指标与次序。对于凸型指数增长失效数据集DS1,多数SRGM模型的接近程度值大于0.5,体现出SRGM模型在凸型指数增长数据集上具有良好的拟合预测能力,其中基于不完美排错假设的M-7模型性能最好,M-10模型次之;基于复杂指数型故障检测率的M-6和M-12的性能最差。对于S型增长失效数据集DS2,相较于DS1整体的接近程度指标值稍低,说明SRGM模型对于S型增长数据集的拟合预测能力稍弱,其中基于不完美排错假设的M-12模型性能最好,M-3模型性能次之,基于完美排错假设的M-4和M-5模型的性能最差。对于凹型指数增长失效数据集DS3,基于不完美排错的M-9模型性能最好,M-3模型次之,基于完美排错假设的M-1和 M-5模型的性能最差。对于开放软件数据集DS4与DS5,基于完美排错的M-9和M-10模型性能较好,基于完美排错的M-4模型和不完美排错的M-12模型性能表现较差。
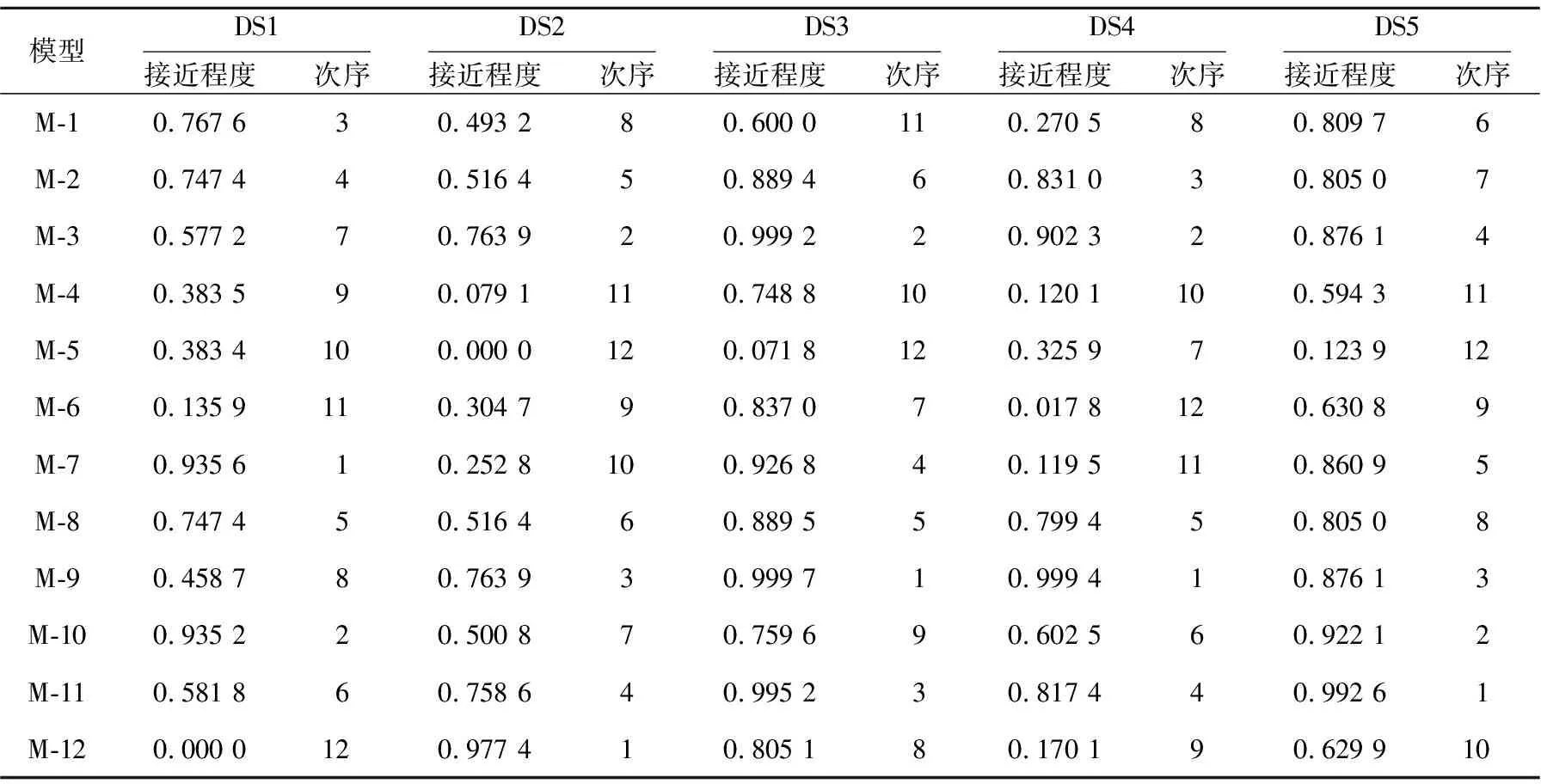
Table 8 Proximity of the models in solution 2
根据表8,对于早期发布的失效数据集(DS1~DS3),基于不完美排错假设的模型(M-7~M-12)的排序性能优于基于完美排错假设的模型(M-1~M-6),表明不完美排错假设的模型更加符合早期的大型软件测试工作,在不同的真实失效数据集上性能更稳定与出色。但是,对于大型开源软件系统的失效数据集,在软件发布后的故障主要来源于开源社区反馈,开发团队对于故障的排除具有周期性、彻底性的特点,因此完美排错模型M-5和M-1在开源软件失效数据集上性能表现良好。
为了进一步分析不同故障检测率函数对SRGM的影响,现对5个数据集上的模型排序序列进行加权平均,求出模型的加权平均次序。对已收集数据集分类统计,将各个失效数据集的权重占比依次设置为0.2,0.2,0.1,0.25,0.1。对偏序序列进行加权计算后结果如表9所示。
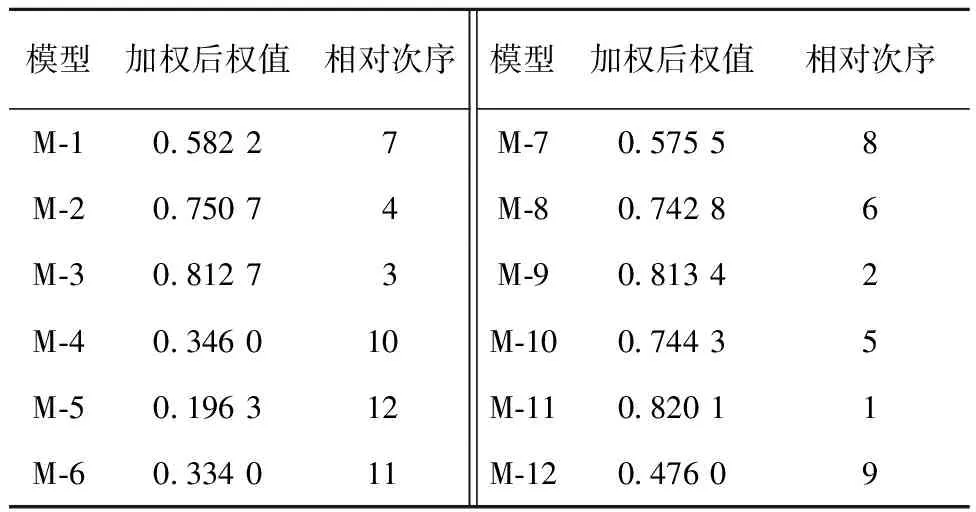
Table 9 Sorting when data sets are weighted
从表9可以看出,大多数基于不完美排错假设的模型的性能要比完美假设的更好,说明考虑不完美排错假设的模型更加符合实际软件测试工作,因此普遍适用性更强,在不同真实失效数据集上性能更稳定与出色。
最后,对基于不同假设的SRGM进行加权处理,以探究不同故障检测率对软件可靠性影响。对于权重的选择,考虑到基于不完美排错假设的模型更具有参考意义,故将其权重设置为0.5,将完美排错假设的模型的权重设置为0.5,得到的排序权重与次序如表10所示。幂函数类型与第1个S型FDR的综合性能位列第1梯队,在不同数据集上、不同SRGM假设中性能最为出色,2个复杂指数型FDR的综合性能最差。幂函数类型FDR描述了在软件测试中故障检测率随着软件运行时间的增加逐渐提高,即随着测试时间的增加,对于故障的检测能力越强,这与现实生活中大多数软件测试环境一致。S型FDR对应更加灵活、复杂的测试环境,其对应的SRGM模型也获得了较好的性能。复杂指数型FDR呈现出了随测试时间递减与先增后减的变化趋势,这与一般真实测试环境相去甚远,故对应的SRGM性能最差。

Table 10 Sorting when SRGMs are weighted
4.3 讨论
方案1与方案2最后的故障检测率FDR的次序值并不完全相同,这表明对于特定的数据集,故障检测率对于SRGM模型的性能影响因素还需要结合历史故障数据、失效数据量和程序规模等信息。另一方面,在单一数据集单一假设基础上分析故障检测率对SRGM性能影响仍存在一些局限性,最终导致2个方案的b(t)函数偏序排序结果不完全相同。
根据本文所选择真实失效数据集与SRGM模型,可对6个FDR函数进行性能排序,结果为b3(t)>b2(t)>b1(t)>b4(t)>b5(t)>b6(t),按照b(t)的类型进行排序,结果为S型1>幂函数类型>常数类型>S型2>复杂指数型。
b(t)对应的SRGM性能优劣与真实失效数据集的性质有联系,故障检测率随时间递增的幂函数FDR对应的SRGM模型在凸型指数增长的数据集上性能突出,S型FDR具有更高的灵活性,在众多数据集上性能突出,体现出适应性广的特性。复杂指数型的b5(t)更适用于不完美排错假设下的SRGM模型。
探究故障检测率FDR对SRGM模型的影响可以帮助测试人员建立性能优秀的软件可靠性模型,进而在测试过程中对故障数量、软件系统总体可靠性、测试成本和软件发布时间进行估计,以达到控制软件测试成本、加强软件管理和确定软件发布时间等目的。
5 结束语
本文研究了不同FDR模型对于SRGM模型性能的影响,并进行了实证分析。首先,回顾了不同类型的故障检测率b(t)形式,共有常量类型、幂函数类型、S型、指数型共4种类型6个表达式。随后,针对单SRGM单FDS多FDR模式、多SRGM多FDS多FDR模式,利用信息熵联合TOPSIS决策算法,得出软件故障检测率函数对应的SRGM模型的偏序序列,分析FDR对SRGM模型的性能影响因素。通过实验发现,幂函数类型FDR在凸型增长数据集上表现出色,指数型在S型增长与凹型增长数据集上表现较好,S型FDR具有较强的柔韧性,适用于不同的数据集,综合性能最好。本文研究对于选择合适的故障检测率函数建立软件可靠性模型有一定的指导意义,并为测试资源分配和确定最优发布时间提供参考。

