改进搜索机制的单纯形法引导麻雀搜索算法*
刘成汉,何 庆
(贵州大学大数据与信息工程学院,贵州 贵阳 550025)
1 引言
20世纪90年代以来,群智能优化算法凭借其简单的结构和优秀的求解性能被研究人员广泛关注。随着研究的不断深入,各种优秀的群智能优化算法被相继提出,例如:粒子群优化PSO(Particle Swarm Optimization)算法[1]、灰狼优化GWO(Grey Wolf Optimization)算法[2]、鲸鱼优化算法WOA(Whale Optimization Algorithm)[3]、秃鹰搜索BES(Bald Eagle Search)算法[4]、蜉蝣算法MA(Mayfly Algorithm)[5]和黏菌算法SMA(Slime Mould Algorithm)[6]等。这些智能算法已被成功应用于路径规划[7]、图像分割[8]和神经网络优化[9]等多种优化问题上。
麻雀搜索算法SSA(Sparrow Search Algorithm)[10]是由薛建凯于2020年提出的一种新型群智能优化算法。SSA是基于自然界麻雀种群的捕食行为和侦察机制提出的,具有参数少、寻优性能强等优点。然而,群智能算法普遍存在收敛速度慢、精度低和易早熟收敛的问题,SSA也不例外。因此,针对上述问题,许多研究人员对SSA做出了改进,例如:吕鑫等人[11]提出了一种混沌麻雀优化算法,采用混沌序列初始化种群并对陷入局部最优个体进行混沌扰动,从而提高了算法搜索能力;毛清华等人[12]在SSA中引入正弦余弦算法和莱维飞行相关思想更新种群位置,平衡了算法的局部搜索能力和全局开发能力;Ouyang等人[13]使用K-means聚类方法对麻雀的个体位置进行聚类和区分,提高了算法的稳定性和鲁棒性;Zhu等人[14]提出了一种自适应麻雀搜索算法,通过引入自适应学习因子提高了SSA的收敛速度;Yuan等人[15]利用重心反向学习策略初始化SSA种群并引入变异算子更新加入者位置,提高了算法搜索效率。虽然上述改进策略在一定程度上改善了SSA的寻优能力,但SSA仍存在收敛慢和易陷入局部最优的问题。
针对SSA的局限性,本文提出了一种改进搜索机制的单纯形法引导麻雀搜索算法SMSSA(Simplex Method guided with improved search mechanism Sparrow Search Algorithm),分别对麻雀种群中发现者的搜索机制和侦察者的侦察机制进行改进,同时引入单纯形法对算法每次迭代中适应度较差的部分个体进行收缩、扩张和压缩操作,以提高算法性能。最后通过8个基准函数、Wilcoxon秩和检测以及部分CEC2014测试函数的仿真实验,验证了本文改进算法的有效性。
2 麻雀搜索算法
SSA的灵感来源于自然界中麻雀种群的捕食和侦察预警行为。一个麻雀种群中存在发现者、加入者和侦察者3种个体。发现者在搜索空间中拥有较好的位置并带领其它发现者觅食。侦察者随机产生,负责侦察预警。算法起源于一个由n只麻雀组成的种群X,X由式(1)所示的矩阵所示:
(1)
其中,D表示问题维度,n表示种群数量,X中每一行表示一只麻雀的位置向量。
在一个麻雀种群中,发现者通常有很高的能量储备,能为其他搜寻者提供觅食区域或方向[10]。发现者位置更新数学模型如式(2)所示:
(2)
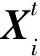
加入者在发现者的带领下进行觅食,加入者具备抢夺发现者食物从而改变身份成为发现者的能力,同时部分未获得食物的加入者飞往其他区域觅食。加入者位置更新数学模型如式(3)所示:
(3)

侦察者大约占种群总数的10%~20%,它们在种群中随机产生,负责预警危险。侦察者位置更新数学模型如式(4)所示:
(4)
其中,Xbest为全局最优位置;β控制步长,是服从正态分布的随机数;K是[-1,1]的随机数;fi、fg和fw分别表示当前个体适应度值、当前全局最佳适应度值和最差适应度值;ε为常数,作用是防止出现分母为零的情况。
3 改进麻雀搜索算法
3.1 改进发现者搜索机制
发现者负责搜索具有丰富食物的区域,并为其它个体提供搜索方向,是整个种群运作的核心,因此发现者的搜索能力对整个算法的收敛起着重要作用。由式(2)可知,当搜索范围内没有出现捕食者时,发现者的位置更新算子存在一定的随机性,这种随机性可能会导致算法稳定性降低,收敛速度变慢。针对上述问题,本文改进了SSA的发现者搜索机制,改进后的发现者位置更新数学模型如式(5)所示:
(5)
其中,k为调节因子,通过k值可以自适应调节发现者位置更新算子下降速率,k值越大,算子下降速率越大。
由式(5)可知,改进的位置更新公式中引入了迭代次数t,使发现者位置更新算子随迭代次数增加呈非线性变化,增加了算法的多样性;同时,结合调节因子k,可自适应调节位置更新算子的下降速率,平衡了算法的搜索能力;最后,发现者位置更新脱离了随机因子α的影响,算法更加稳定。
3.2 改进侦察机制
在原始SSA中,当侦察者预警到危险(即意识到有陷入局部极值的风险)时,对于处于种群中心的侦察者,SSA选择让其靠近邻居以减少被捕食的风险,这样会导致算法陷入局部最优值而停止搜索;对于处在种群边缘的侦察者,SSA利用随机步长控制侦察者向安全区域靠近,而这种随机步长可能会导致算法收敛速度变慢。
针对SSA侦察机制中存在的局限性,本文通过引入新的侦察因子来改进SSA的侦察机制。对于处于种群中心的侦察者,通过非线性递增的侦察因子Ф1使其逐步远离当前位置,防止算法陷入局部最优值;对于处在种群边缘的侦察者,采用非线性递减的侦察因子Ф2代替随机步长因子,在保证侦察者安全的同时使其逐步靠近最优位置,加快算法收敛。Ф1和Ф2的数学模型如式(6)所示:
(6)
其中,Фs和Фl分别表示侦察因子的初始值和最终值,Tmax为最大迭代次数,μ为非线性调节系数。
3.3 单纯形法策略
单纯形法在多维优化问题中表现出色,具有鲁棒性高、局部优化能力强和参数简单等优点[16]。单纯形法通过对适应度较差的个体进行反射、扩张、压缩和收缩的操作来改变个体位置,其中反射操作能使个体反方向搜索,扩大个体搜索空间;扩张操作使个体远离最优解,防止算法陷入局部极小值点;压缩和收缩操作能使个体更加接近最优位置。其具体实现步骤如下所示:
Step1初始化种群,计算个体适应度值并排序,记录全局最优个体位置Xb和次优个体位置Xt以及它们的适应度值fb和ft,Xc定义为Xc=(Xb+Xt)/2。
Step2对m个位置较差的点w进行反射操作,Xr=Xc+α(Xc-Xw),其中α表示反射系数。
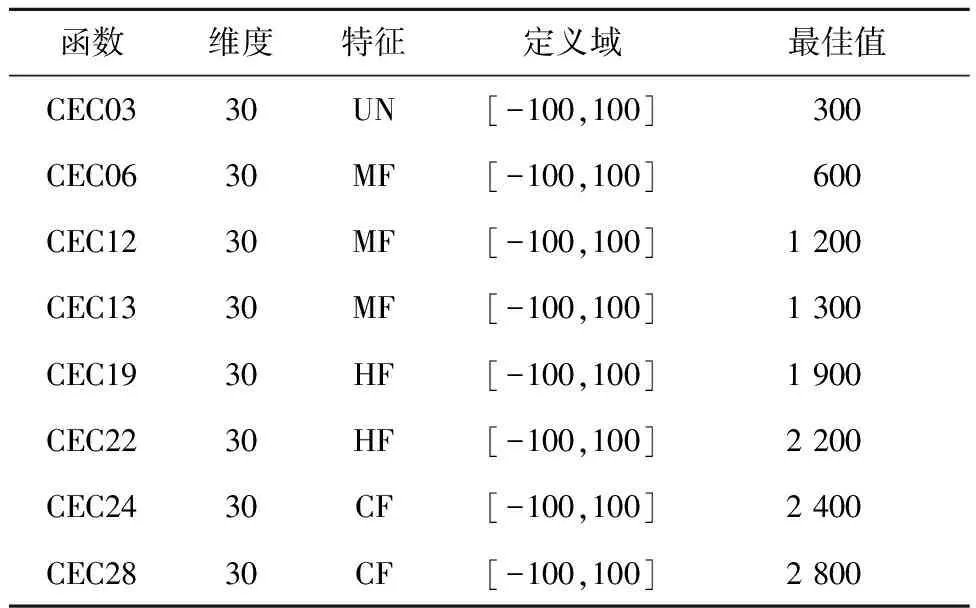
Step3判断,如果fr Step4判断,如果fr Step5判断,如果fw>fr>ft,则进行收缩操作,Xs=Xc-σ(Xw-Xc),σ为收缩系数,且σ=γ;如果fs 为了改善SSA求解速度慢、精度不高的问题,本文算法在每次迭代结束时,对位置较差的m个麻雀个体进行单纯形法操作,以增强SSA的搜索能力。 SMSSA实现步骤如下所示: 步骤1初始化种群和SMSSA参数:Tmax为最大迭代次数,n为种群规模,ub和lb为搜索上下界,D为维度,P为发现者比例。 步骤2计算个体适应度值并排序,记录最优、次优和最差适应度个体位置:Xb、Xt和Xw,及它们的适应度值fb、ft和fw。 步骤3根据式(5)更新发现者位置。 步骤4根据式(3)更新加入者位置。 步骤5根据式(6)更新侦察者位置。 步骤6定义Xc=(Xb+Xt)/2,对m个位置较差的个体w进行反射操作,Xr=Xc+α(Xc-Xw),反射个体适应度值为fr。 步骤7根据单纯形法判断fr、fb、fw和ft之间大小关系,然后决定对适应度最差的m个个体行执行扩张、压缩或伸缩操作。 步骤8循环执行步骤2~步骤7,判断是否满足迭代条件,满足则跳出循环。 步骤9算法结束,返回最优位置及其适应度值。 本文仿真实验采用的计算机配置为:Intel Core i5-7500U,32 GB内存,64 bit操作系统,计算环境为Matlab2016(a)。为了检验SMSSA的性能,本文选取PSO算法、GWO算法、WOA和SSA与SMSSA进行对比,基本参数设置为:最大迭代次数Tmax=500,种群规模n=30,维度D=200,500,1000,各算法内部参数设置如表1所示。 Table 1 Parameters setting 表1中,SSA的参数P为发现者所占比例;PSO算法的参数c1和c2为粒子的学习因子,wmax和wmin分别为惯性因子的最大值和最小值;WOA的参数b为常数,用来定义鲸鱼优化算法螺旋更新位置时螺旋的形状;SMSSA的相关参数介绍见第3节。 为了测试SMSSA在基准函数上的寻优效果,本文采用了8个基准测试函数进行仿真实验,其中f1~f5为单峰测试函数,f6~f8为复杂多峰测试函数。测试函数基本信息如表2所示。 Table 2 Introduction of benchmark functions 为了验证SMSSA中改进策略的优越性,本文还将SMSSA与基本SSA、CSSA(a Chaotic Sparrow Search optimization Algorithm)、SASSA、ISSA(an Improved Sprrow Search Algorithm combining cauchy variation and reverse learning)进行基准测试函数寻优实验对比。其中,CSSA为混沌麻雀搜索算法[11],SASSA为融合K-means的多策略改进麻雀搜索算法[13],ISSA为混合正弦余弦算法和Lévy飞行的麻雀算法[12]。仿真实验维度D=30,种群规模n=30,最大迭代次数Tmax=500,其中CSSA的最大迭代次数为100次,SSA和SMSSA内部参数已由表1给出。每个函数进行30次后求平均值和标准差,实验结果如表3所示。 从表3对比结果可知,对于单峰测试函数f1~f4以及多峰测试函数f6和f7,SMSSA能够收敛到理论上的最优值0;对于复杂多峰测试函数f8,原始SSA陷入了局部最优值,而SMSSA能够跳出局部极值,并收敛到接近理论最优值;对于单峰测试函数f5,虽然SMSSA没有收敛到0,但是相比于其他SSA和SSA变体,其收敛精度有一定提升;虽然CSSA迭代次数只有100次,但是SMSSA在迭代100次时的结果也优于CSSA的,对于f1函数,SMSSA在迭代100次时收敛精度比CSSA高48个数量级,在相同参数设置下,SMSSA对于其他函数寻优的收敛精度也都高于CSSA。上述分析表明,本文提出的SMSSA相较于其他SSA变体具有明显优势。 Table 3 Performance comparison of the improved algorithms Figure 1 Comparison of the average convergence curves of the optimization algorithms on 200 dimensional benchmark functions 为了验证SMSSA在面对高维问题时的求解能力,仿真实验将PSO算法、GWO算法、WOA和SSA与SMSSA进行高维基准函数寻优性能对比,参数统一设置为:种群规模n=30,最大迭代次数Tmax=500,维度D=200,各算法相关参数参考表1。对于200维基准测试函数,各函数独立运行30次的平均收敛曲线如图1所示。 从图1可以看出,SMSSA在高维函数的优化上有很大优势,相比于其他优化算法,SMSSA不管是在收敛速度和精度上还是在跳出局部最优的能力上都有很大提升。对于单峰测试函数f1~f4,SMSSA在200维时仍然能够找到理论全局最优解,这说明本文提出的改进发现者搜索机制能够提高算法的收敛精度;对于复杂多峰测试函数f6和f7,SMSSA能在50次迭代以内找到最优值,比SSA和WOA收敛更快,这说明本文引入的单纯形法操作能加快算法收敛,提高算法搜索能力;对于单峰测试函数f5和多峰测试函数f8,SMSSA能够跳出局部极小值干扰,收敛到更接近于理论最优值,这说明改进的侦察机制对于提高算法跳出局部最小值的能力有一定帮助。 上节给出了SMSSA在200维基准测试函数上的寻优对比测试,SMSSA表现良好。本节对SMSSA进行超高维基准函数寻优实验,参数统一设置为:维度D=500,1000,种群规模n=30,最大迭代次数Tmax=500,选取PSO算法、GWO算法、WOA和SSA与SMSSA进行超高维基准函数寻优性能对比,各算法相关参数参考表1,实验结果如表4所示。 从表4可以看出,当维度达到500维时,PSO算法、GWO算法、WOA和SSA的寻优收敛结果出现指数级增加;SSA在基准测试函数的寻优上,与30维度时的寻优结果相差10个数量级,基本失去寻优能力;GWO算法、WOA和SSA在基准测试函数的寻优上也均有多个指数量级的出入;对于500维和1 000维单峰测试函数f1~f4和多峰测试函数f6、f7,SMSSA仍然能够收敛到理论最优值;对于测试函数f5和f8,SMSSA收敛精度也优于其他对比算法。这说明SMSSA对于超高维问题的优化同样具有较好的稳定性和鲁棒性。 Table 4 Performance comparison of the optimization algorithms on ultra-high dimensional benchmark functions 为了进一步验证SMSSA的优化性能,本文采用Wilcoxon秩和非参数统计检验方法检验SMSSA与SSA、PSO算法、GWO算法、WOA、SSA1、SSA2和SSA3之间在统计上存在的显著差异,其中SSA1、SSA2和SSA3是SSA的变体,分别表示本文改进发现者搜索策略的SSA、改进侦察机制的SSA和引入单纯形法的SSA。本文选取了12个基准测试函数的仿真结果进行秩和统计分析,假设对比数据结果优于SMSSA的概率为p,如果p值很小,说明原假设情况的发生概率很小。当p<5%时,可以被认为是拒绝零假设的有力验证[17]。实验结果中,“+”表示SMSSA秩和统计结果优于对比算法;“-”表示SMSSA秩和统计结果差于对比算法;“=”表示SMSSA秩和统计结果等于对比算法;没有检测结果用NaN表示。Wilcoxon秩和检验结果如表5所示。 从表5可以看出,SMSSA与其他算法的秩和统计对比结果中80%的p值小于5%,这说明从统计学上来说,SMSSA对于基准函数的寻优结果优势是明显的,从而进一步验证了ISMA的优越性。 为了评价SMSSA对于更复杂的混合以及复合类型函数的求解能力,本文采用部分具有复杂特征的CEC2014测试函数进行仿真实验。CEC2014测试函数相关信息见表6,其中UN表示单峰函数,MF表示多峰函数,HF表示混合函数,CF表示复合函数。选取基本SSA、PSO[18]、SCA[17]和L-SHADE[20]与SMSSA进行实验对比,其中L-SHADE在CEC2014测试函数上表现优秀,常被用于对比实验。实验参数统一设置为:种群规模n=50,最大迭代次数Tmax=2000,维度D=30,各函数独立运行30次后取平均值和标准差。实验结果如表7所示。 Table 6 Part of the CEC2014 functions 从表7可以看出,SMSSA求解复杂函数的性能总体优于其他对比算法。虽然SMSSA在单峰CEC03函数上寻优结果略差于L-SHADE的,但在多峰函数、混合函数和复合函数的求解上,SMSSA的求解能力远高于L-SHADE的,对于CEC12、CEC13和CEC19测试函数,SMSSA基本能够找到最优值,对于多峰CEC06函数及其它复合函数,SMSSA也能收敛到最优值附近,说明SMSSA在求解复杂问题上同样具有很好的鲁棒性。 设SSA的时间复杂度为O(N×Tmax×D),其中,n为种群规模,Tmax表示最大迭代次数,D为函数维度。SMSSA的时间复杂度包括基本SSA时间复杂度、改进搜索机制的SSA时间复杂度和引入单纯形法的SSA时间复杂度3个部分。由于改进发现者搜索机制和改进侦察机制并未对算法时间复杂度造成影响,因此改进搜索机制的SSA时间复杂度为O(n×Tmax×D),引入单纯形法的SSA的时间复杂度为O(n×Tmax×D)+O(m×Tmax×D)=O(n×Tmax×D)。 由此可知,本文提出的SMSSA时间复杂度与SSA时间复杂度一致,且SMSSA算法稳定性更高,寻优性能远高于SSA。 针对基本麻雀搜索算法存在的收敛速度慢、易陷入局部极值点的问题,本文提出了一种改进搜索机制的单纯形法引导麻雀搜索算法(SMSSA);考虑到麻雀种群中发现者和侦察者在搜索中存在的局限性,本文改进了发现者搜索机制和侦察者侦察机制,提高了算法的搜索能力,改善了算法易早熟收敛的问题;通过引入单纯形法中的反射、扩张、收缩和压缩操作,帮助种群中位置较差的个体向较好位置移动,提高了算法的收敛速度。通过8个基准测试函数以及部分CEC2014测试函数的仿真对比实验以及Wilcoxon秩和检测,验证了SMSSA的有效性。下一步工作考虑将SMSSA应用到实际工程优化问题中,进一步验证SMSSA在处理实际问题时的鲁棒性。 Table 7 CEC2014 function optimization comparison3.4 SMSSA实现步骤
4 仿真实验及结果分析
4.1 参数设置说明

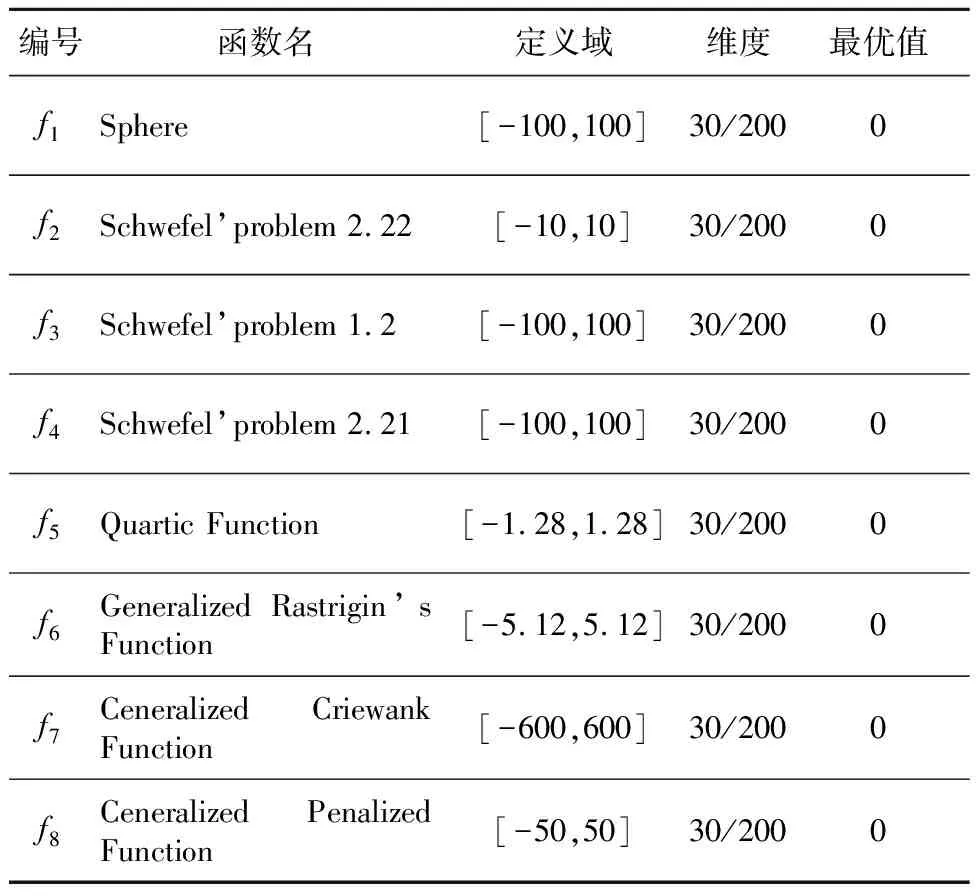
4.2 基准测试函数说明
4.3 与其他改进SSA性能对比


4.4 各算法高维寻优性能对比
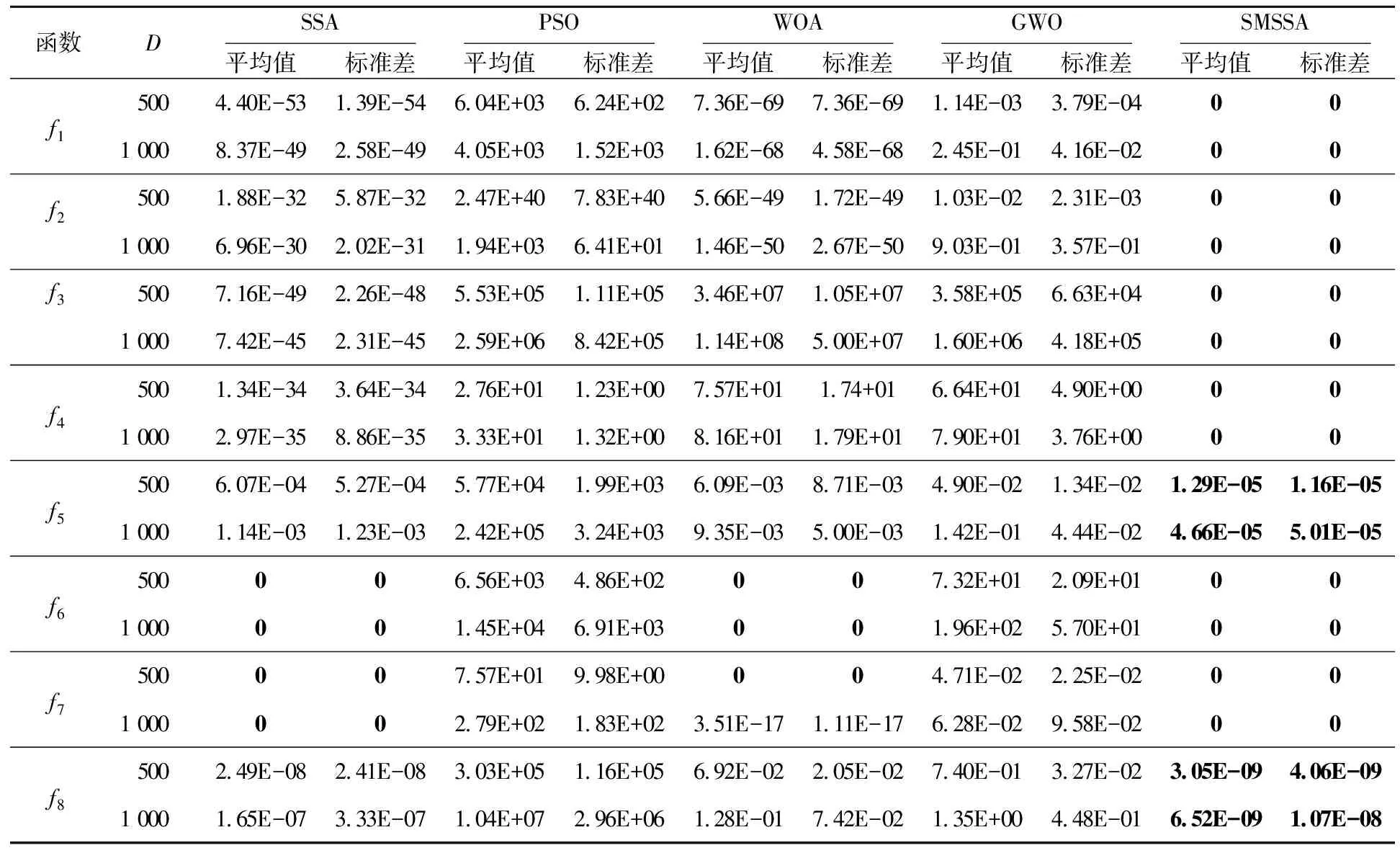
4.5 SMSSA超高维寻优测试
4.6 Wilcoxon秩和检测
4.7 CEC2014测试函数仿真对比
4.8 SMSSA时间复杂度分析
5 结束语