面向多智能体博弈的并行蒙特卡洛树搜索算法研究*
管延霞,刘逊韵,刘运韬,谢 旻,徐新海
(1.国防科技大学计算机学院,湖南 长沙 410073;2.军事科学院战争研究院,北京 100091)
1 引言
计算机博弈是衡量人工智能发展水平的重要测试平台之一[1],已在象棋、围棋等棋类博弈的决策问题上取得了优异的成果[2,3]。计算机博弈目前的研究重点在于多智能体博弈。
多智能体会导致博弈过程中的动态空间和状态空间呈指数级增长,使得决策的搜索和选择过程需要消耗一定的时间和计算资源[4]。计算机资源的并行协作可以有效降低多智能体博弈中的维度灾难等问题。但是,该方法的主要难点在于如何有效利用计算资源并行加速搜索过程,以及如何实现信息的有效传递。
本文选取Pommerman[5]作为研究平台,针对多智能体博弈问题中的蒙特卡洛树搜索算法展开研究。Pommerman是一种通过放置炸弹来淘汰敌人的多智能体博弈环境。博弈过程中的搜索算法优化是博弈性能提升的关键,针对原有蒙特卡洛树搜索算法搜索耗时过长的问题,本文借鉴蒙特卡洛树搜索常用的并行方法,对博弈中的搜索阶段进行并行优化,旨在充分利用有限的计算机资源,缩短搜索算法收敛到近似最优决策策略的学习时间。本文具体工作如下所示:
(1)建立了适合并行搜索策略的Pommerman博弈算法——基于胜率估值传递的并行蒙特卡洛树搜索算法,实现了搜索策略框架并行化,构建了多个子进程的并行机制,有效缩短了决策时间,提高了决策效率。
(2)将构建的并行算法应用于Pommerman的不同游戏模式,并分别与对应的原始搜索算法进行了性能对比,定量分析了本文算法的优势。
2 蒙特卡洛树搜索算法并行优化现状
Pommerman博弈平台采用蒙特卡洛树搜索MCTS(Monte Carlo Tree Search)算法[6-9]做出博弈策略,该搜索算法将蒙特卡洛算法应用于博弈树搜索过程中。围棋中的AlphaGo[2,3]即是以MCTS算法为基础进行研发的。
MCTS算法是在搜索空间巨大的情况下仍然有效的算法。与MCTS算法出众的表现相对应,庞大的搜索空间使得MCTS算法在决策时耗费了更长的时间[10]。因此,研究蒙特卡洛树搜索算法的并行优化十分必要[11-13]。文献[14]表明,蒙特卡洛树搜索算法可以使用如图1所示的叶并行化(Leaf Parallelization)、树并行化(Tree Parallelization)和根并行化(Root Parallelization)3种不同的方法进行并行化。3种并行方法的优劣不同,叶并行化实现简单但缺乏节点探索性;树并行化可以最小化通信开销但会导致节点的过度开发;根并行化虽然减少了进程通信但同时也减少了每个进程的博弈模拟次数,也在一定程度上降低了决策的准确性。
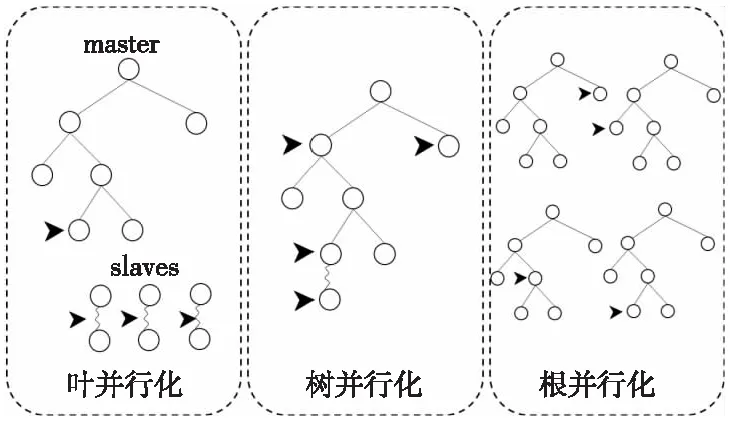
Figure 1 Mainstream parallelization methods of Monte Carlo tree search algorithm
在对MCTS进行并行优化设计时,不仅要考虑如何跟踪得到正确的统计数据,还要尽量减少进程之间的通信开销。
MCTS算法依赖当前游戏状态之前的采样信息[15]来保持未知领域的探索和已有经验的利用之间的平衡。当使用多个工作程序并行化蒙特卡洛树搜索算法部署时,要确保每个工作程序都能获得最新的统计信息。在并行化过程中,本文想要尽可能实现如图2a所示的理想并行化,减少如图2b所示真实并行化可能会出现的进程冲突等问题。

Figure 2 Parallelization of Monte Carlo tree search algorithm
3 基于胜率估值传递的并行蒙特卡洛树搜索算法
3.1 算法设计
基于多个进程根节点回报值汇总的思想,本文提出了一种基于胜率估值传递的并行蒙特卡洛树搜索算法。算法借鉴Root Parallelization[7]的思路,如图3所示,在进行MCTS搜索之前主进程将当前的游戏状态及游戏策略传递给各子进程,并将探索任务平均分配到各子进程中,使多个子进程基于同一个根节点状态独立并行执行搜索过程。每个子进程完成探索任务后,将回报信息传递给主进程,主进程依据最终的汇总信息进行决策并更新搜索策略。主进程将更新后的信息再次传递给子进程,循环反复直至游戏状态满足结束条件。
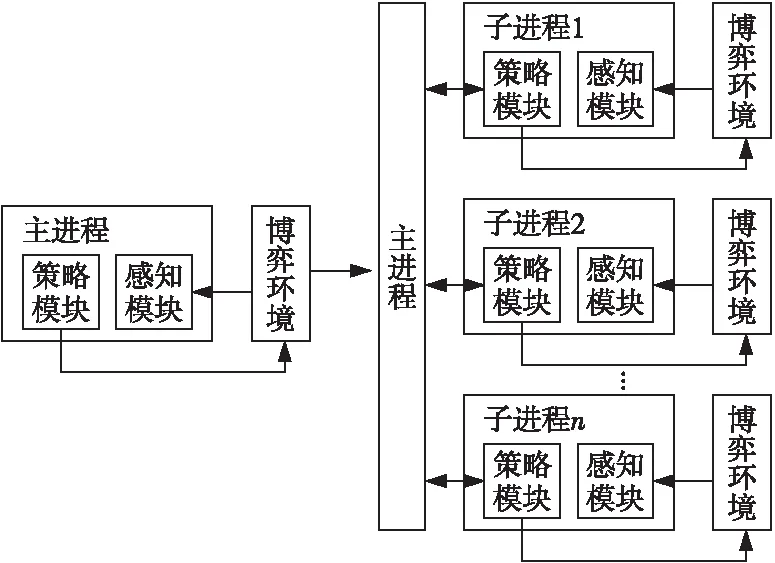
Figure 3 Parallelization of search process
只在进程的开始和结束时进行算法进程之间的信息交互,以最小化子进程之间的信息交互。相比于采用树并行化实现的Ary[16]来说减少了进程交互;相比于叶并行化的实现,避免了节点频繁加解锁;相较于根并行化的实现,本文设计的算法各子进程的搜索耗时相当,减少了子进程信息收集的等待时差。本文设计的算法能够有效利用计算资源,缩短搜索时间,提高MCTS的搜索效率。
图4给出了实现并行化的搜索过程,主要分为4步:
(1)游戏开局,参数初始化,主进程给子进程分配任务,并行执行子进程;
(2)各子进程根据 MCTS算法完成规定次数的迭代,产生根节点下所有合法行动的胜率估值,得到该子进程下的胜率估值向量,并将其发送给主进程;
(3)主进程汇总各子进程的胜率估值向量,选择获胜概率最大的行动,并以此为依据,做出决策行动;
(4)待对方智能体决策执行后,再重复进行步骤(2)操作,直到博弈终止。
本文提出的蒙特卡洛树并行搜索算法的典型特征是当各子进程得到各自根状态下的所有行动的胜率估值,并将该子进程的胜率估值向量传递给主进程后,主进程采用式(1)汇总所有子进程的胜率估值向量。
(1)
其中,X表示汇总的胜率估值向量;n表示划分的子进程数量;wi表示第i个子进程所占比重,在本文中每个子进程分配的迭代次数相同,所以假设每个子进程对应的贡献度相同,即wi=1/n;xi表示第i个子进程计算所得的胜率估值向量。智能体依据汇总的胜率估值向量X选取对当前局面最有利的决策行动。
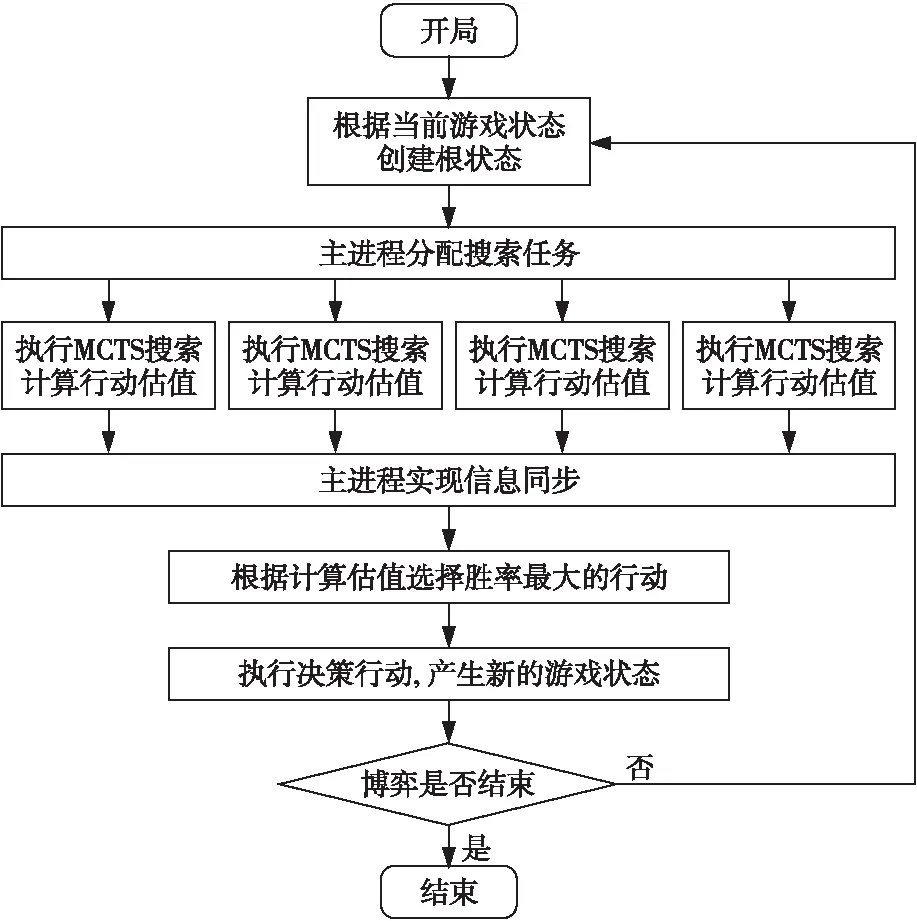
Figure 4 Flow chart of multi-process game search
3.2 并行蒙特卡洛树搜索算法的实现
本文提出的蒙特卡洛树并行搜索算法流程如算法1所示。
算法1并行MCTS算法
输入:当前游戏状态(非游戏终态)。
输出:基于当前游戏状态做出的决策行动。
步骤1构建多个子进程进行搜索:
每个进程均以当前游戏状态作为根节点,独立并行执行步骤2~步骤7。
步骤2判断子进程博弈模拟局数是否达到要求:
if满足条件
执行步骤8,输出决策行动;
else
执行步骤3;
步骤3判断当前游戏状态是否符合终止状态:
if符合
执行步骤7;
else
执行步骤4;
步骤4选择节点:
if当前状态在博弈树中不存在
执行步骤5,拓展当前游戏状态;
else
执行步骤6,选择最佳的子节点;
记录节点状态、action和环境reward;
步骤5拓展节点:
将当前状态添加到博弈树中,同时初始化当前状态下的所有动作节点所对应的游戏状态,执行步骤4。
步骤6状态更新:
按照式(2)计算每个节点的value值,选择值最大的节点的状态并将其更新为当前游戏状态:
(2)
假设智能体进行决策时共有m种行动可供选择,即当前节点有m个子节点,第j个节点具有参数yj,cj(j∈[1,m]),cj表示到该次模拟为止第j个节点被选中的次数,yj表示第j个节点在cj次的模拟中模拟获胜的次数。yj/cj表示第j个节点的胜率。
步骤7奖励回溯:
根据步骤3记录的节点、action和环境reward,反向更新沿途节点reward和访问次数。完善博弈树构建;
游戏状态回到当前状态,执行步骤2。
步骤8胜率估值向量合并:
根据式(1)合并各子进程根节点下的胜率估值向量,根据式(2)计算当前状态根节点下适合的决策行动。
步骤9输出基于当前游戏状态作出的决策行动。
将待决策的当前游戏局面作为根节点,子进程并行进行蒙特卡洛树搜索,得到子进程胜率估值,由主进程进行合并得到最终的胜率估值向量,算法根据胜率估值向量,选取决策行动。
4 模型测试与数据分析
4.1 非零和多智能体博弈平台-Pommerman简介
Pommerman游戏界面如图5所示,每局游戏有4个智能体,每个智能体以网格4角为起始位置。每个智能体的目标就是存活到最后,通过炸弹的放置以及躲避炸弹等博弈策略来淘汰敌人,保全自己。在Pommerman竞赛中,智能体只能做出如表1所示的行动之一,不能做出其他多余动作。

Figure 5 Game interface of Pommerman

Table 1 Legal actions of agent in Pommerman
另外,竞赛中还存在不同的竞争模式,在团队模式(2V2)中,当一个团队的2个智能体都被摧毁时,游戏结束,获胜队伍为幸存智能体所在队伍;在4个智能体的单人模式(FFA)和2个智能体的单人模式(1V1)中,最多只有1个智能体存活时游戏结束,幸存者即为获胜者。
4.2 实验环境
本文的软件与硬件实验环境分别如表2和表3所示。本文基于表2和表3的实验环境,进行对比实验的设计与实现,所有的实验都是基于相同的运行时间(24 h)采用不同搜索算法的智能体进行博弈,测试博弈性能并进行数据分析。
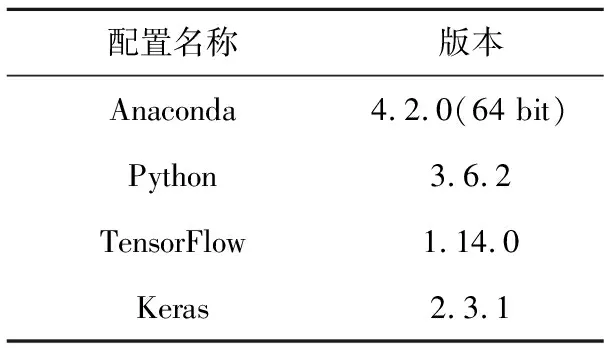
Table 2 Experimental environment(software conditions)

Table 3 Experimental environment(hardware conditions)
4.3 测试指标
在对蒙特卡洛树搜索算法进行测试之前,为了方便对比并分析并行版本与串行版本的蒙特卡洛树搜索算法的性能,本文使用以下2个测试指标进行性能分析:
(1)对局耗时:即在相同的MCTS迭代次数之下,测试不同并行进程蒙特卡洛树搜索算法的平均每局耗时,即对同一个任务需要消耗的时间的对比。平均对局耗时可以反映不同进程的蒙特卡洛树搜索算法在搜索过程中的耗时情况。
(2)对弈胜率:对弈胜率用于度量搜索算法的性能,即智能体使用不同版本的博弈算法进行对弈,记录使用本文设计的优化算法的智能体获胜的概率。在本文中不同版本的博弈算法对弈的设计如表4所示。将不同版本的博弈算法运用至不同的博弈模型(FFA,2V2和1V1),分析博弈效果。

Table 4 Comparative experiment design
4.4 性能分析
为了有效对比分析不同版本蒙特卡洛树搜索算法的性能,实验设置中串行版本和并行版本的MCTS迭代次数均设置为400,并且为了使并行版本的MCTS迭代平均分布到不同子进程中,并行版本设置的子进程数量分别为2,4和8。这样能够在充分利用有限计算机资源的同时,均衡实现子进程的MCTS搜索。
4.4.1 对局耗时
本次实验的实验对象是表4中的实验1、实验2和实验4、实验5,串行MCTS与并行MCTS分别运行相同的时间(24 h)。记录实验1、实验2和实验4、实验5完成的对弈局数,FFA模式和2V2模式的结果如图6和图7所示。
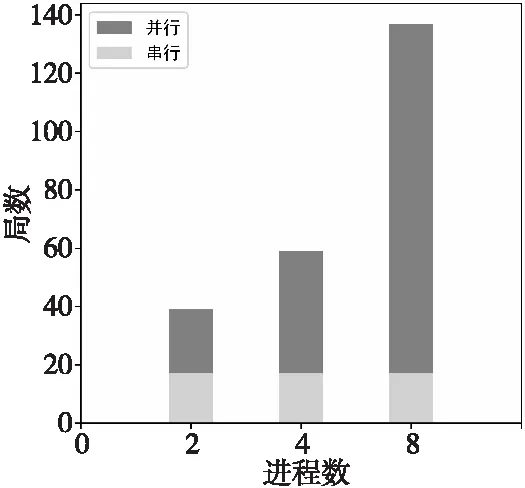
Figure 6 Number of games(FFA)
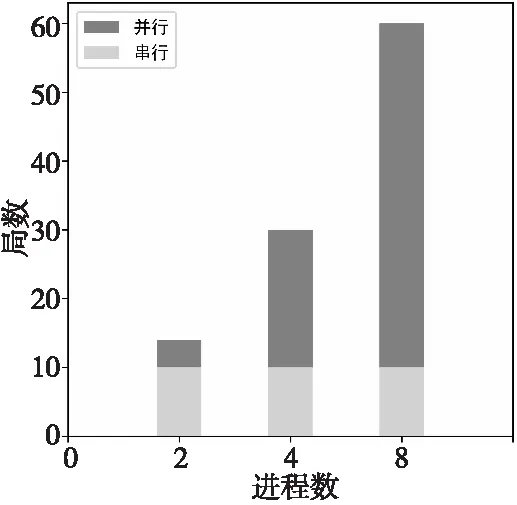
Figure 7 Number of games(2V2)
通过图6和图7固定时间博弈局数的数据分析本文设计的算法的耗时。在FFA模式下,子进程数量为2的情况下,对局完成的时间约为串行完成时间的40%。2V2模式下,子进程数量为2的情况下,对局完成的时间约为串行完成时间的25%。这验证了本文设计的基于胜率估值传递的并行蒙特卡洛树搜索算法可以有效缩减博弈树的搜索时间。
4.4.2 对弈胜率
由4.4.1节的数据分析可以得到,在FFA模式下,本文设计的基于胜率估值传递的并行蒙特卡洛树搜索算法会将搜索时间大约缩短为原来的1/n(n为并行的子进程数量),在大幅缩短搜索时间的同时也降低了胜率。为了探索胜率不变的情况下,搜索时间最多能够缩短多长时间,本节实验选取了迭代次数不同的串行智能体与并行智能体进行对抗。
本节按照表4中实验3的配置进行设计,在博弈局数相同的情况下,不同迭代次数的串行MCTS与不同子进程下并行MCTS智能体进行对弈,实验结果如图8所示。本文将子进程数为2、迭代次数为200的并行MCTS与迭代次数为150的串行MCTS进行对弈。统计结果如表5所示,数据变化曲线如图8所示。通过图8可以得出,随着博弈局数的增加,并行MCTS胜率在数据0.5上下波动,并行智能体与串行智能体的博弈能力不相上下,两者对弈胜率相近。
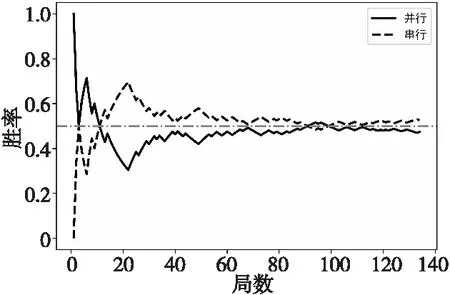
Figure 8 Winning rate of parallel MCTS agents vs serial MCTS agents when playing chess
本文对表5和图8的数据分析,验证了本文设计的基于胜率估值传递的并行蒙特卡洛树搜索算法的有效性。基于表4中实验3的实验配置,本文设计的并行MCTS算法在有效缩短约20%搜索时间的情况下,与串行MCTS智能体对抗获胜的胜率约为50%。进一步验证了在有效缩短搜索时间的情况下,本文设计的基于胜率估值传递的并行蒙特卡洛树搜索算法未对博弈性能造成影响。

Table 5 Parallel MCTS vs serial MCTS
本文通过对弈耗时与对弈胜率2个指标值的分析,验证了本文设计的基于胜率估值传递的并行蒙特卡洛树搜索算法是可行且有效的,提高了MCTS中博弈树的搜索效率。
5 结束语
基于Pommerman博弈平台,本文在蒙特卡洛树搜索算法的并行优化的理论基础上,设计并实现了基于胜率估值传递的并行蒙特卡洛树搜索算法,并给出了算法的详细步骤。本文通过一系列的对比实验来对优化的并行蒙特卡洛树搜索算法进行测试并评估其性能,实验结果表明,本文设计的基于胜率估值传递的并行蒙特卡洛树搜索算法在与原有博弈算法保持相同博弈胜率的情况下,能够至少缩短20%的搜索时间。
未来的研究重点将集中于尝试将蒙特卡洛树搜索与深度强化学习策略相结合,例如叶子节点第1次展开时可以用策略网络获得先验评分;探索一种CPU与GPU异步工作的方案,在提高算法在博弈树中搜索效率的同时,更加充分地调用计算资源,避免GPU资源的浪费。

