几类线性码的扩展码及其在密钥共享中的应用*

李晓茹,衡子灵,李文婷

(长安大学理学院，陕西 西安 710064)

1 引言

令q为素数p的方幂，r=qm，m为整数且m>1，Fr表示有r个元素的有限域，α为Fr的本原元。

1.1 线性码及其扩展码

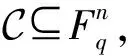
A(z)=1+A1z+A2z2+…+Anzn

(1)

称为C的重量计算器。重量分布可以用来刻画线性码纠错和检错的出错概率,是线性码理论中的重要研究课题，有大量文献研究了线性码的重量分布[1-4]。

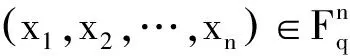
x1+x2+…+xn+1=0}

(2)

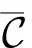
1.2 极小码及其在密钥共享中的应用

设C是参数为[n,k]的线性码，c=(c1,c2,…,cn)∈C。定义c的支撑集supp(c)={i:ci≠0,1≤i≤n}。设c′∈C为任意与c线性无关的码字。如果supp(c′)⊄supp(c)总成立，那么称c为极小码字。极小码字可以用来描述基于线性码构造的密钥共享方案的访问结构。

密钥共享方案是一种设计秘密拆分方式和恢复方式的方法。设P表示参与者构成的集合。秘密共享的基本思想是将秘密以适当的方式拆分，拆分后的每一份由P中的每一个参与者管理，单个参与者无法恢复信息，只有被授权的P的某个子集Γ中的所有参与者共同协作才能恢复秘密信息。被授权的子集Γ称为访问结构。1993年，Massey[6]利用线性码构造出密钥共享方案，并建立了访问结构和对偶码极小码字之间的联系。然而，线性码的极小码字一般很难确定，它和完全译码问题密切相关。2006年，Yuan等[7]提出利用一类特殊线性码—极小码来构造安全高效访问结构上的密钥共享方案,所有码字都是极小码字的线性码称为极小码。Ashikhmin等[8]给出了如下判定线性码为极小码的充分条件:

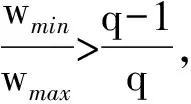
根据引理1，很多研究人员[1-3,7,9]构造出了可用于构造密钥共享方案的极小码。

1.3 本文主要工作

令Trr/q表示从Fr到Fq的迹函数，其中Trr/q(x)=x+xq+…+xqm-1，x∈Fr。特别地，单位元素0的完全反象Trr/q-1(0)称为迹函数Trr/q的核，记为ker(Trr/q)。

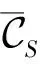
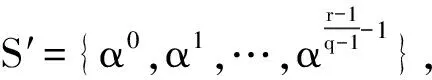
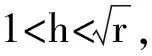
上述3个构造所得的线性码均为极小码，从而都可用于构造安全高效访问结构上的密钥共享方案。

2 数学基础

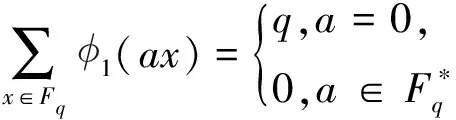
(3)

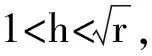
(4)

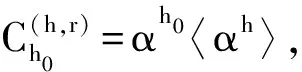
(5)

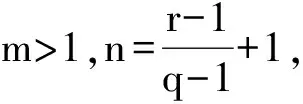
(6)

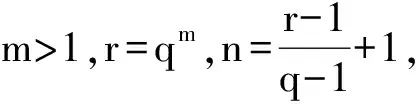
Trr/q(bαn-1),cn+1):

(7)

该扩展码是[n+1,m,qm-1]三重码，其重量计数器如式(8)所示：

A(z)=1+(qm-2-1)zqm-1+2(qm-1-qm-2)zqm-1+1+

(qm-2qm-1+qm-2)zqm-1+2

(8)

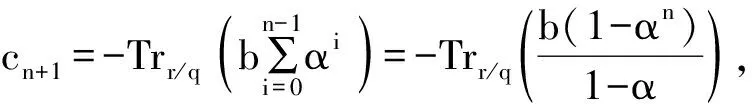
(9)

令：

从而有式(10)成立：

(10)

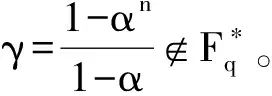
(11)

□

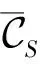
(12)

从而可得CS的重量计数器。

□

Trr/q(bαn-1),cn+1):

(13)

是[n+1,m,qm-1-1]三重码，其重量计数器为A(z)=1+(qm-1-qm-2)zqm-1-1+(qm-2qm-1+2qm-2-1)zqm-1+(qm-1-qm-2)zqm-1+1。

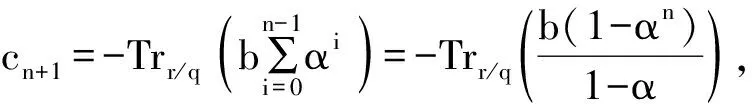
(14)

(15)

令:

从而有式(16)成立:

(16)

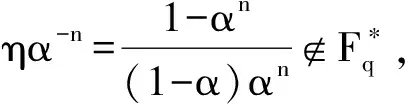
(17)

□

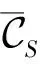
4 扩展码的参数和重量分布

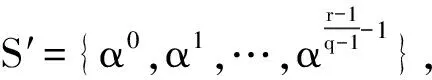
引理5很容易证明，过程略去。

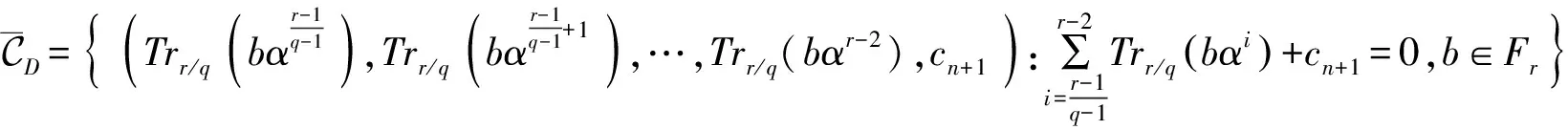
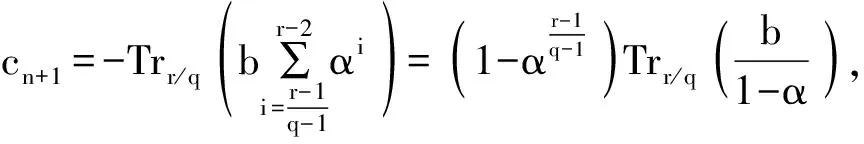
(18)

□

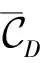
5 扩展码的参数和重量分布

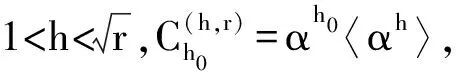
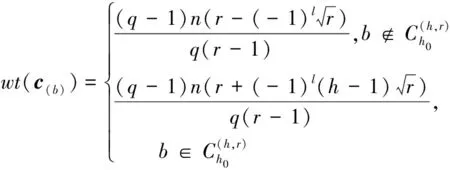
(19)

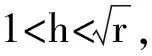
Trr/q(bα(n-1)h),cn+1):

(20)

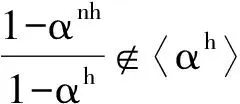
证明由于

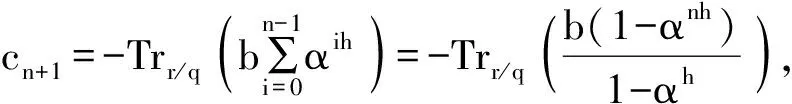
(21)

令:

从而有式(22)成立：

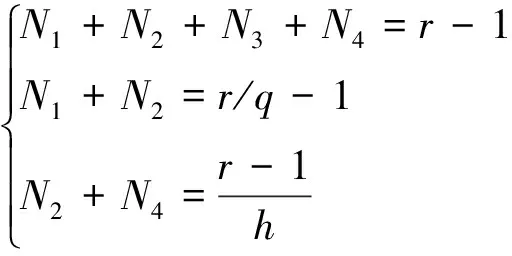
(22)

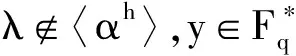
(23)

□

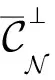
6 结束语

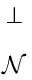
Table 1 Some optimal or almost optimal codes