双自回归模型下基于EM算法的分位数回归分析
袁晓惠, 杜 让, 胡 茜
(长春工业大学 数学与统计学院, 吉林 长春 130012)
0 引 言
股票价格能够体现一个国家的经济状况,股市的波动也时刻影响着个人和企业对股票的投资情况。当前,中国经济飞速发展,国家经济市场面临机遇和挑战,经济主体潜在的风险和不确定性日益凸显,基于线性相关系数的分析方法不再适用于研究股票市场的发展。基于此,黄义[1]研究了金融股票市场与房地产市场价格指数的动态相关性。袁晓惠等[2]针对我国2011-2018年消费者信心指数的经济数据拟合阈值自回归模型,选出模型的自回归参数,并估计阈值点。马育欣等[3]对股票收盘价序列进行经验模式分解(EMD),并对分解后的本征模函数(IMF)与残差序列分别拟合ARMA-GARCH模型。
近20年来,双AR(p)模型受到人们的关注,Francq C等[4]针对非线性过程提出双AR(p)模型,可作为一种弱ARMA模型;Ling S[5]研究了双AR(p)模型的平稳遍历条件,得出模型中参数的极大似然估计是渐近正态的结论;Zhu K等[6]研究双AR(p)模型的拟极大似然估计,发现该方法比加权一乘方法更具优越性;玄海燕等[7]提出双AR(p)模型的一种混成检验,再次验证了双AR(p)模型在股价预测中的优越性。
目前有关该模型的研究大多局限于对均值的建模,假定误差项服从正态分布。当数据为非正态时,模型的拟合效率会降低,甚至错误推断。作为一类稳健模型,分位数回归不仅放宽了模型假设,还可以刻画不同分位点上的数据表现,成为稳健统计分析的首选模型之一[8-10]。对于经典的双AR(p)模型,其分位数回归参数估计的计算较难实现。Zhu Q等[11]修正了模型假设,将之转化成线性形式,从而在一般分位数回归的理论框架下讨论参数估计。然而,针对经典双AR(p)模型分位数回归的计算问题,我们至今未检索到相关文献。因此,文中尝试在双AR(p)模型的基础上对其分位数回归进行计算。
在线性分位数回归问题的研究中,Tian Y等[12]将EM算法引入线性复合分位数回归模型,通过迭代加权进行最小二乘估计;Yang F[13]提出了一种分位数回归模型的随机EM算法,估计效果良好。
文中运用EM算法对双AR(p)分位数回归模型进行参数估计,提出了两阶段迭代加权估计,并考察其在不同分位点上的表现。模拟研究表明,文中所提EM算法在分位数回归估计中表现出色。
1 双AR(p)模型的分位数估计
考虑经典的双AR(p)模型[5-6]
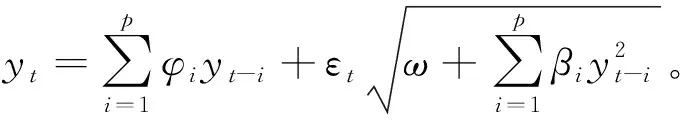
(1)
其中,φi∈R,ω>0,βi≥0(1≤i≤p),并且{εt}是独立同分布的白噪声序列。令
φ=(φ1,φ2,…,φp)T,
β=(β1,β2,…,βp)T,
Y1t=(yt-1,yt-2,…,yt-p)T,
则模型表示为
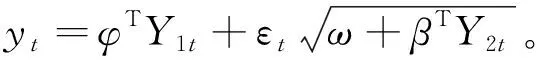
(2)
通常假定{εt}是正态白噪声,可以得到模型参数的最小二乘估计。
研究此模型在不同分位点上的表现,类似于Koenker R等[8]提出的分位数回归理论,第τ分位点下的估计为
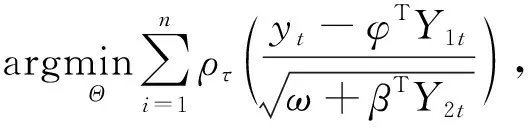
(3)
其中,Θ={φ,ω,β},ρτ(μ)=μ{τ-I(μ<0)}是分位数回归的损失函数,I(·)为示性函数。但上述优化问题的求解较为困难,文中通过构造EM算法求解此模型的参数估计。
2 EM算法
2.1 似然
在分位数回归领域,非对称拉普拉斯分布(ALD)越来越受到关注,根据Yu K等[9]基于ALD似然函数的贝叶斯分位数回归思想,最小化目标损失函数
ρτ(μ)=μ{τ-I(μ<0)},
(4)
相当于在ALD误差下最大化似然函数。ALD的概率密度函数为
(5)
式中:μ----位置参数;
σ----尺度参数;
τ----偏度,τ∈(0,1)。
即使对真实值的估计有一定的误差,估计结果依旧是稳健的。
运用Kozumi H等[10]提出的概率重构方法,将式(4)置于误差分布为非对称拉普拉斯分布的极大似然估计理论上。该误差项{εt}的分布可以表示为指数分布和正态分布的混合表达:
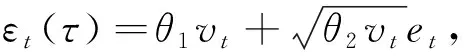
(6)
其中,
vt~exp(1),
et~N(0,1)。
令
γ=(ω,β)T,
ht(γ)=ω+βTY2t=γTY3t,
则模型等价于
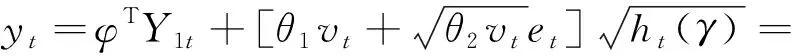
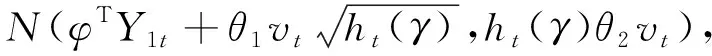
(7)
则有
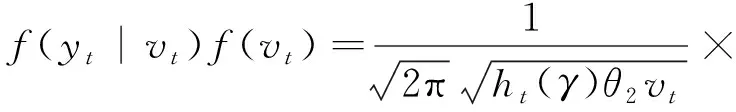
exp{-vt},
(8)
vt的条件概率密度函数为
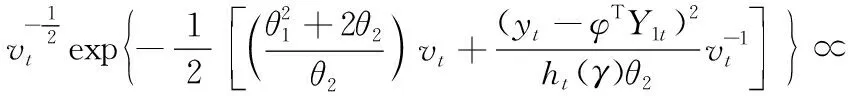
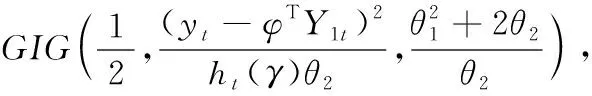
(9)
由此得到
(10)
完全数据{yt,vt}下的条件似然函数为
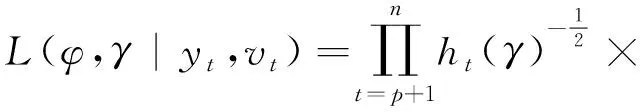
(11)
取对数,求得对数似然
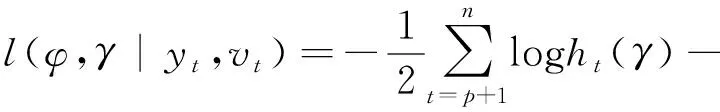
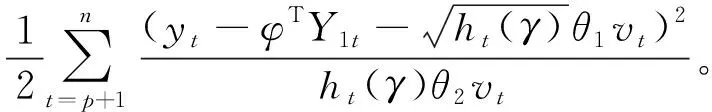
(12)
2.2 算法
对于含有潜变量的概率模型参数估计问题,通过EM算法迭代可以进行局部最优求解。令Θ=(φ,γ),设初始值为Θ(0),给定第t次迭代值Θ(t),然后利用EM算法通过迭代E步和M步来搜索模型的极大似然估计值。该算法从Θ(0)开始迭代,然后在两步之间交替。E表示期望,M表示最大化,EM算法计算过程如下:
E步:基于第t次的迭代值Θ(t),似然函数第(t+1)次的期望值为
Q(Θ|Θ(t))E[l(Θ|yt,vt)|Θ(t)]=
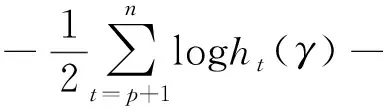
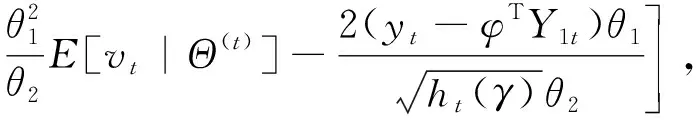
(13)
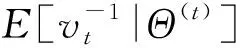
M步:将E步中的Q函数最大化,求导得到估计方程
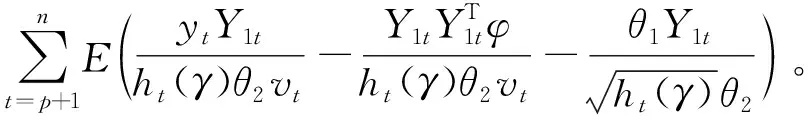
令导函数为零,有
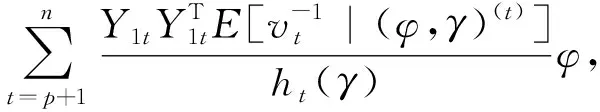
(15)
求解,得到第(t+1)步φ的估计值为
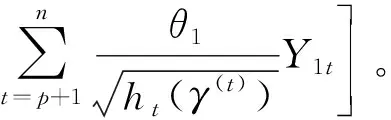
(16)
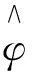
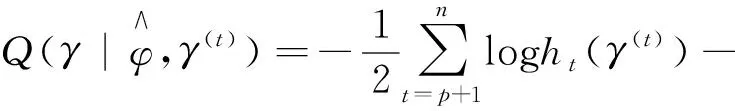
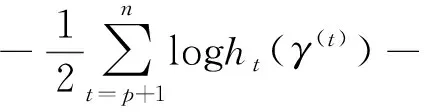
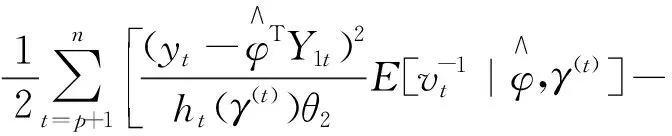
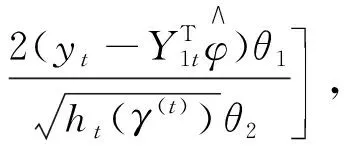
(17)
得到γ的估计
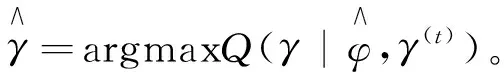
(18)
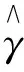
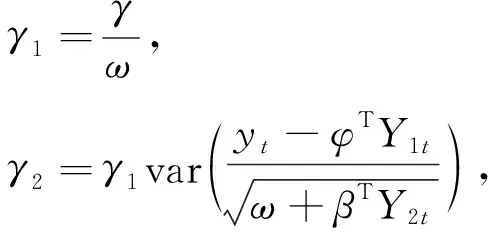
(19)
γ2即为所求γ的估计值。
具体算法过程如下:
1)设定初值(φ,γ)(0),由E步计算出Q(φ(1)|(φ,γ)(0));
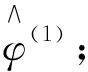
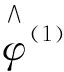
4)将得到的(φ,γ)(1)估计值返回1),重复1)~3),当满足条件‖(φ,γ)(t+1)-(φ,γ)(t)‖≤10-5时,停止迭代;
5)对γ的估计值标准化,最终得到参数估计结果。
3 BIC准则
BIC准则又称贝叶斯信息准则,可用于模型的选择,通过加入模型复杂度的惩罚项来避免过拟合问题。借鉴Wang H等[14]提出的广义贝叶斯信息准则,得到:
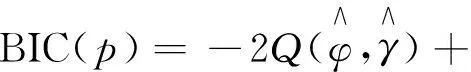
(2p+1)log(n-pmax),
(20)
其中p在{1,2,…,pmax}上搜索,pmax为给定的最大阶数,n为样本量,Q为EM算法中E步似然函数期望值。
4 模 拟
通过模拟验证双AR(p)分位数回归模型在有限样本下的表现,基于模型
产生随机数。其中,εt(τ),ht(γ)的形式参见式(6)。
设定回归系数为
φ=(φ1,φ2)T=(0.1,0.2)T,
γ=(ω,β1,β2)T=(0.2,0.5,0.2)T。
4.1 参数估计
对上述分位数回归模型进行拟合,令n=100、500和1 000。分别讨论分位点τ为0.3、0.5和0.7时的估计,通过EM算法迭代,并进行1 000次模拟试验,列出相应参数估计值的偏度、标准差和均方误结果。不同分位点τ参数估计模拟结果分别见表1~表3。
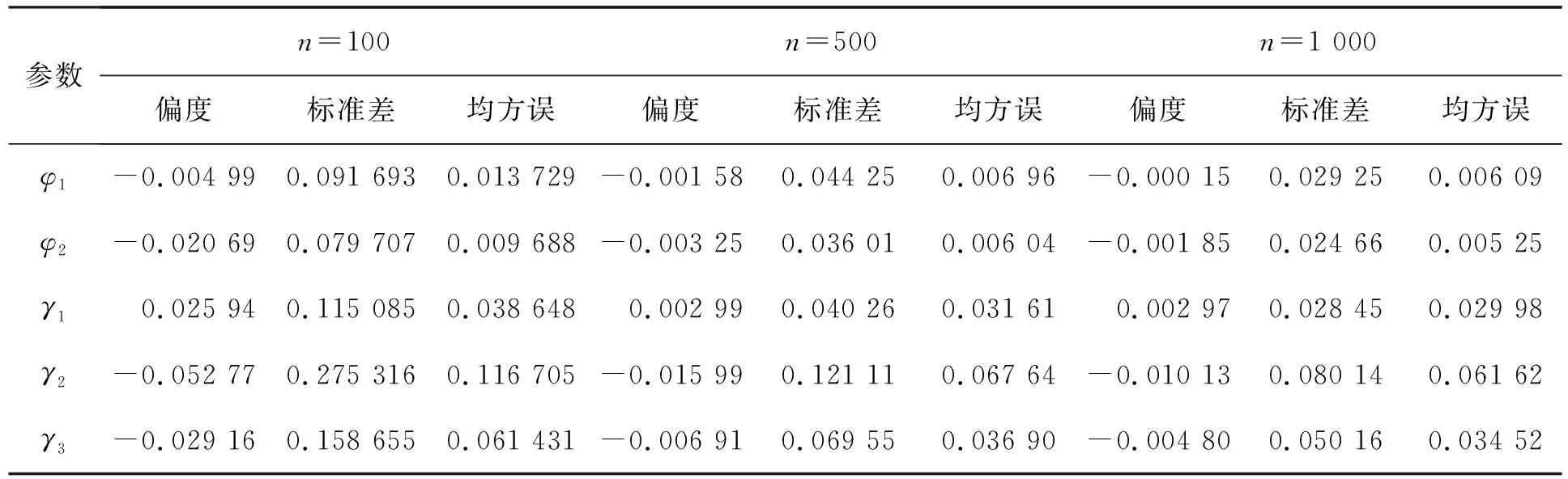
表1 参数估计模拟结果(τ=0.3)
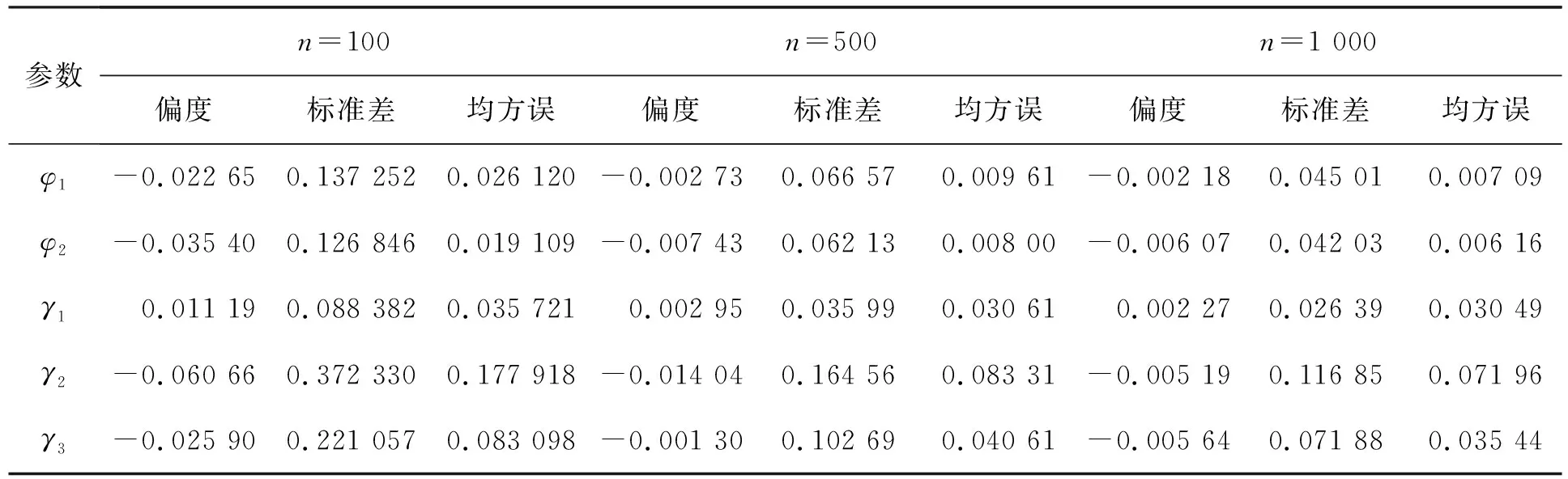
表2 参数估计模拟结果(τ=0.5)

表3 参数估计模拟结果(τ=0.7)
以上结果可以看出,随着样本量的增大,三个分位点下估计的均方误都减小,说明估计具有相合性,EM算法在模型估计中表现较好。
4.2 BIC定阶
通过BIC准则对双AR(p)分位数回归模型进行参数选择,在4.1节模拟的基础上,假定最大阶数pmax为4,在{1,2,…,pmax}上搜索最优阶数,通过式(20)求出BIC值最大时对应的阶数p,即为最优阶数。
以τ=0.5为例,通过模型
从表中可以看出,在对角线上元素的取值最高,即模型选到与真值相同阶数的频率很高。当n=300时,BIC准则选择效果明显好于n=100,说明BIC准则进行模型选阶,样本量较大时,结果更为准确。
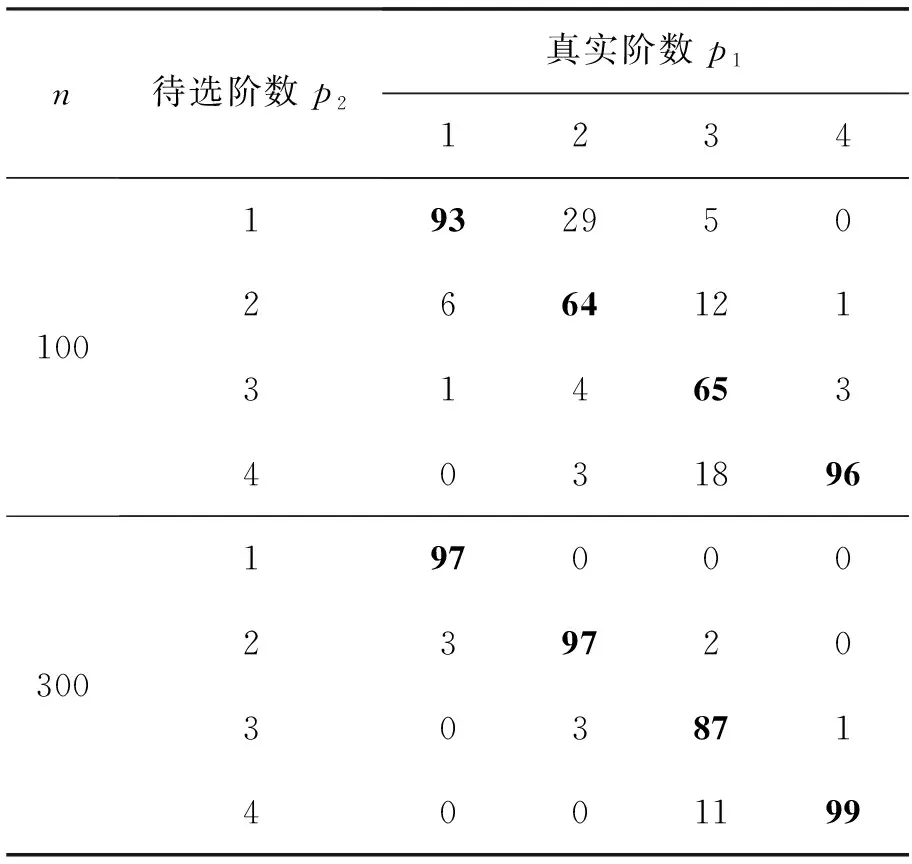
表4 BIC待选频数表
5 实 证
研究金融市场的发展规律,一般选取综合性强,能反映经济整体趋势发展的指数,以确保结论能够符合大多数情况,沪深300指数(399300)可以反映中国证券市场股票价格变化的整体趋势。因此,文中选取沪深300指数的部分收盘价数据进行分析,以2018年1月2日至2021年7月27日的收盘价数据作为观测值,2021年7月28日至2021年7月30日的数据作为预测值数据,共870个样本。数据来源于网易财经(http://quotes.money.163.com/1399300.html)。
沪深300指数收盘价数据的时间序列图和ACF图如图1所示。

(a) 时序图 (b) ACF图
由时序图可知,在有限时间内,观测数据波动性较大,数据不平稳。由ACF图可以看出,样本数据具有很强的自相关性。由于文中研究的模型在所给条件下是严平稳的,我们对原始数据进行平稳化处理,采用一阶对数差分变换,并做单位根检验,检验的p值小于0.01,即变换后的数据为平稳序列。
对处理后的数据作回归分析,分别对τ取0.3、0.5和0.7,通过BIC准则在p={1,2,3,4}上选取合适的阶数,结果见表5。
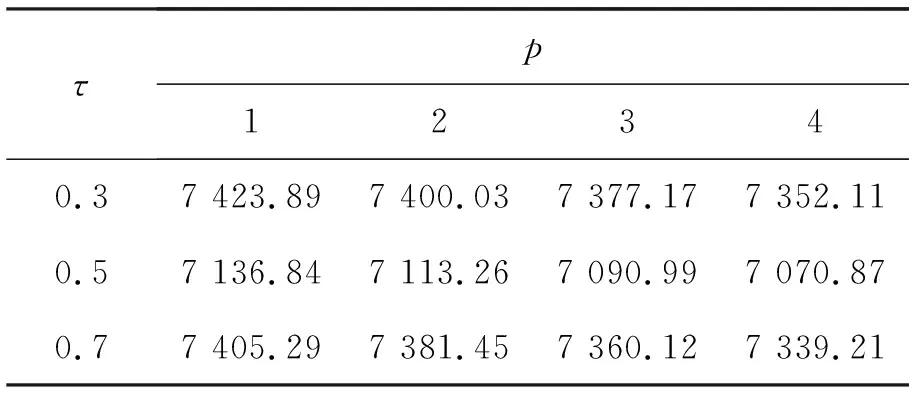
表5 最优阶数选择BIC值
可以看出,在三个分位点上,BIC最大时对应的p值均为1,所以,文中选取双自回归维数p=1。应用双AR(p)分位数回归模型对沪深300指数进行模拟,分别得到在τ分位点为0.3、0.5和0.7上的三种模型估计,估计结果见表6。
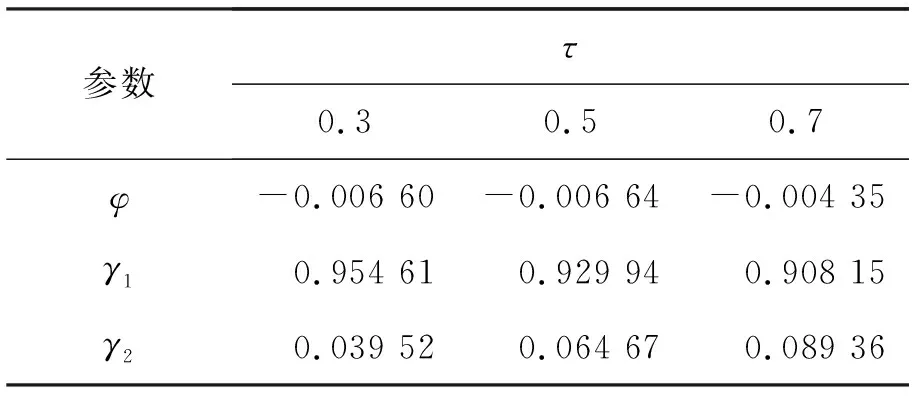
表6 参数估计结果
由此得到如下模型。
模型一(τ=0.3):
yt=-0.006 60Y1t+
模型二(τ=0.5):
yt=-0.006 64Y1t+
模型三(τ=0.7):
yt=-0.004 35Y1t+
基于以上三种模型对2021年7月28日至2021年7月30日的股价进行预测,结果见表7。

表7 预测结果
由表7可以看出,不同分位点下的预测值和真实数据都非常接近,且变化趋势相近,说明文中提出的模型对沪深300指数的预测结果较为准确,模型是有效的。
6 结 语
考虑双AR(p)分位数回归模型,首先运用EM算法分别对不同分位点下的参数进行估计。模拟研究发现,参数中对非零真值估计的均方误很小,且随着样本量的增大,均方误也越来越小,估计效果较好;其次,通过BIC准则选取模型阶数的最佳p值,阶数选择结果准确,正确率较高。最后对沪深300指数的股价数据进行实证研究,验证了模型的有效性。

