求解快递车辆配装问题分支限界算法

赵秦怡，赵榆琴

（大理大学数学与计算机学院，云南大理 671003）

快递车辆配装问题是指快递公司从配送中心派出车辆向某条路线上快递站点进行货物配送时，还需将快递站点揽收的货物带回配送中心，给出揽收货物的重量及价值，在每个站点只被服务一次的情况下，使得车辆在完成货物配送的同时在每个站点都取回价值尽可能大的货物，车辆配装问题属于背包问题的范畴。

背包问题是指给定一组重量和价值已知的货物和一个有载重限制的背包，如何选择装入背包的货物，使得装入背包的货物价值尽可能大。背包问题是重要的NP困难问题，是典型的组合优化问题，在投资决策、资源分配、装载问题和下料问题的研究中具有重要的理论价值。围绕经典背包问题的研究已取得丰硕成果，文献〔1〕提出了0－1增量背包问题，背包容量可递增；文献〔2〕提出了折扣0－1背包问题，物品不仅有重量和价值维度，且物品价值带有折扣系数；文献〔3〕提出多维背包问题，背包及物品均有多维特征；文献〔4〕提出多维多选择背包问题，在进行物品选择时有多个约束条件的附加；文献〔5〕提出在线背包问题，背包容量可卸载，物品随流水线移动且重量及价值事先未知。

分支限界法是求最优解的有效算法〔6〕，本文提出一种求解快递车辆配装问题带限界函数的分支限界（express vehicle assembling knapsack problem，EVAKNP）算法。

1 EVAKNP问题描述

给定快递车辆运输线路D的m个配送点车辆容量集｛C1，C2，…，Cm｝，m个物品集Pi=｛（v1，w1），…，（vi，wi），…，（vn，wn）｝，其中wi为第i种物品重量，vi为第i种物品价值，物品价值可以和快递货物的投递时间、货物本身的价值等因素相关，物品数量n在m个物品集中取值不同。快递车辆配装问题，以下简称EVAKNP问题，是指依次在m个配送点进行物品配送和配装，在车辆容量变化及物品集变化的情况下如何进行装载，使得经m个配送点后车辆获得最大价值V。原问题可由若干个子问题构成，子问题k指车辆在配送点k卸货，在该站车辆获得Ck的容量，待装载物品集为Pk，如何在Pk中进行物品选择增加车辆价值Vk，使得车辆途经所有配送点后获得最大价值。经m个配送点后，出发时的物品均卸载完，每一次卸载之后获得的容量Ck转换为价值Vk，车辆返回时的价值V=V1+V2+…+Vm。

可以证明车辆返回时的价值V满足最优性原理。设V1为车辆在第一个配送点增加的最大价值，车辆之后增加的最大价值为Vx，则V=V1+Vx，显然V一定是车辆最后获得的最大价值。如若不然，设Vx是车辆在第一个配送点之后增加的最大价值，V1'是在第一个配送点获得的价值且比V1还大，则V1'+Vx是车辆最后获得的价值且比V还大，导致矛盾。同理，在第二个配送点车辆增加的最大价值V2使得Vx最大，以此类推。

快递车辆配装问题的子问题k可形式化描述为：

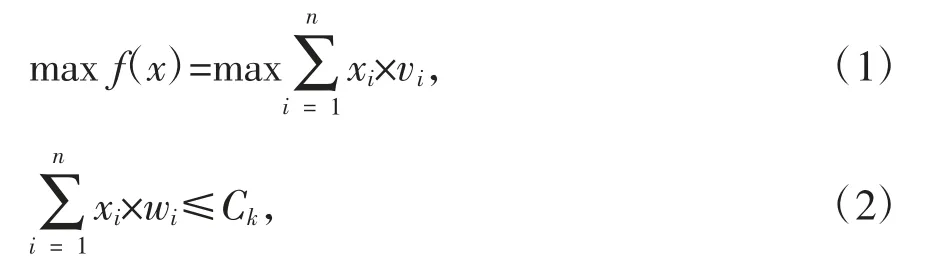
其中，vi和xi是该子问题物品集Pi中物品的价值和重量，Ck为第k个子问题中车辆的剩余容量，xi在集合｛0，1｝中取值，xi=0不装载i号物品，xi=1则装载i号物品。车辆配送问题可形式化描述为：

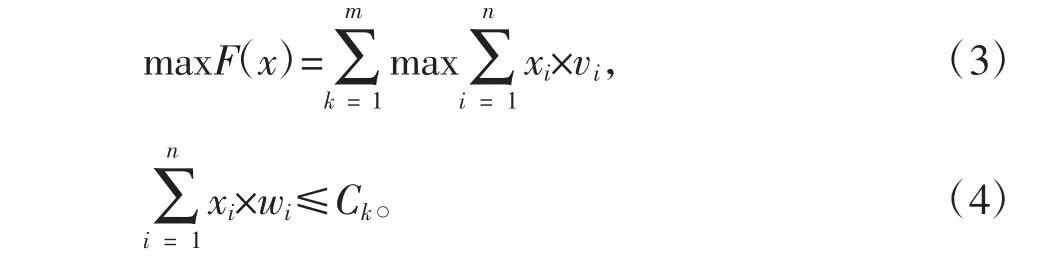
2 EVAKNP算法描述

2.1 算法思想EVAKNP问题求解由m个子问题的求解构成，由式（1）可知第k个子问题的解Vk=max｛Vk1，…，Vki，…｝，Vki是子问题的可行解，Vk是子问题的最优解。在本算法中采用分支限界法求最优解，分支限界法按广度优先策略搜索问题的解空间树，在搜索过程中，待处理结点用限界函数估算目标函数（背包获得的实际价值）的可能取值，在待处理结点中选取使目标函数取得极值的结点优先进行解空间树的广度优先搜索，不断调整搜索方向，尽快找到问题的最优解。

在子问题中，结点目标函数值是指从该结点往下搜索解空间树到达叶子结点使得背包获得的最大价值，由该结点往下的路径可能有多条，背包最后获得的最大价值在解空间树未搜索完的情况下不确定，即该结点的目标函数值不确定。在EVAKNP算法中设计了一个合理的限界函数，在搜索过程中用限界函数值进行目标函数值的估算。先将子问题k物品集合Pi中元素（vi，wi）二元组按物品的单位重量价值进行排序，搜索到第i层的结点t时，已搜索了前i-1个物品，对结点t的搜索过程由第i个物品及后续物品的搜索构成，则有

前i-1个物品获得的价值确定，后续物品的搜索过程未确定，用一个极大值进行估算，将车辆剩余空间全部装载成后续物品中单位重量价值最大的第i号物品。由此，限界函数可设计为：

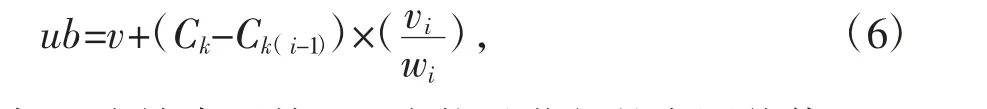
其中，v为搜索了前i-1个物品获得的实际价值，Ck-Ck（i-1）为车辆此时剩余空间，vi/wi为第i种物品的单位重量价值。

EVAKNP算法采用大根堆存储搜索树中生成的结点，堆顶结点的限界函数值最大。首先计算根节点的限界函数值，生成其左右孩子结点到搜索树，优先选取堆中（搜索树中）限界函数值最大的结点（堆顶元素）进行搜索，生成该结点的左右孩子结点插入堆，并进行堆调整，搜索原理在于限界函数值大的结点其目标函数值也趋向于大。重复上述过程，若当前搜索结点是叶子结点e，计算出叶子结点的目标函数值（背包实际获得的价值），如果该值大于堆中其余结点的限界函数值，则已找到最优解，搜索过程结束。由式（6）限界函数的定义可知其余结点的搜索越往下，其目标函数取值趋向于越小，故相较于结点e搜索已无意义。

由式（1）可知，本算法待求解子问题的最优解是解空间树中使目标函数取最大值的叶子节点，在搜索过程中，为尽快获得最优解，可设计一个合理的搜索下界进行搜索树的剪枝，若结点限界函数值小于该下界，由该结点往下搜索得到的叶子结点都不可能是最优解，可进行剪枝。解空间树中任意一个可行解均可作为下界，本算法采用贪心选择法求得的解作为较合理的搜索下界。

例1某EVAKNP问题中，快递车辆容量50，途经3个快递站点，第一个站点卸货之后车辆剩余容量20，待装载物品集｛（50，10），（24，6），（14，7），（5，5）｝，第二个站点卸货之后车辆剩余容量16，待装 载 物 品 集｛（10，1），（12，6），（8，2），（9，3），（6，6）｝，第三个站点卸货之后车辆剩余容量14，待装 载 物 品 集｛（18，3），（10，2），（16，4），（12，4），（6，3），（4，4）｝。原问题的解由3个子问题的解构成，以下是子问题1的求解过程。子问题1的解空间树见图1，叶子结点中重量小于等于20的解都是可行解。

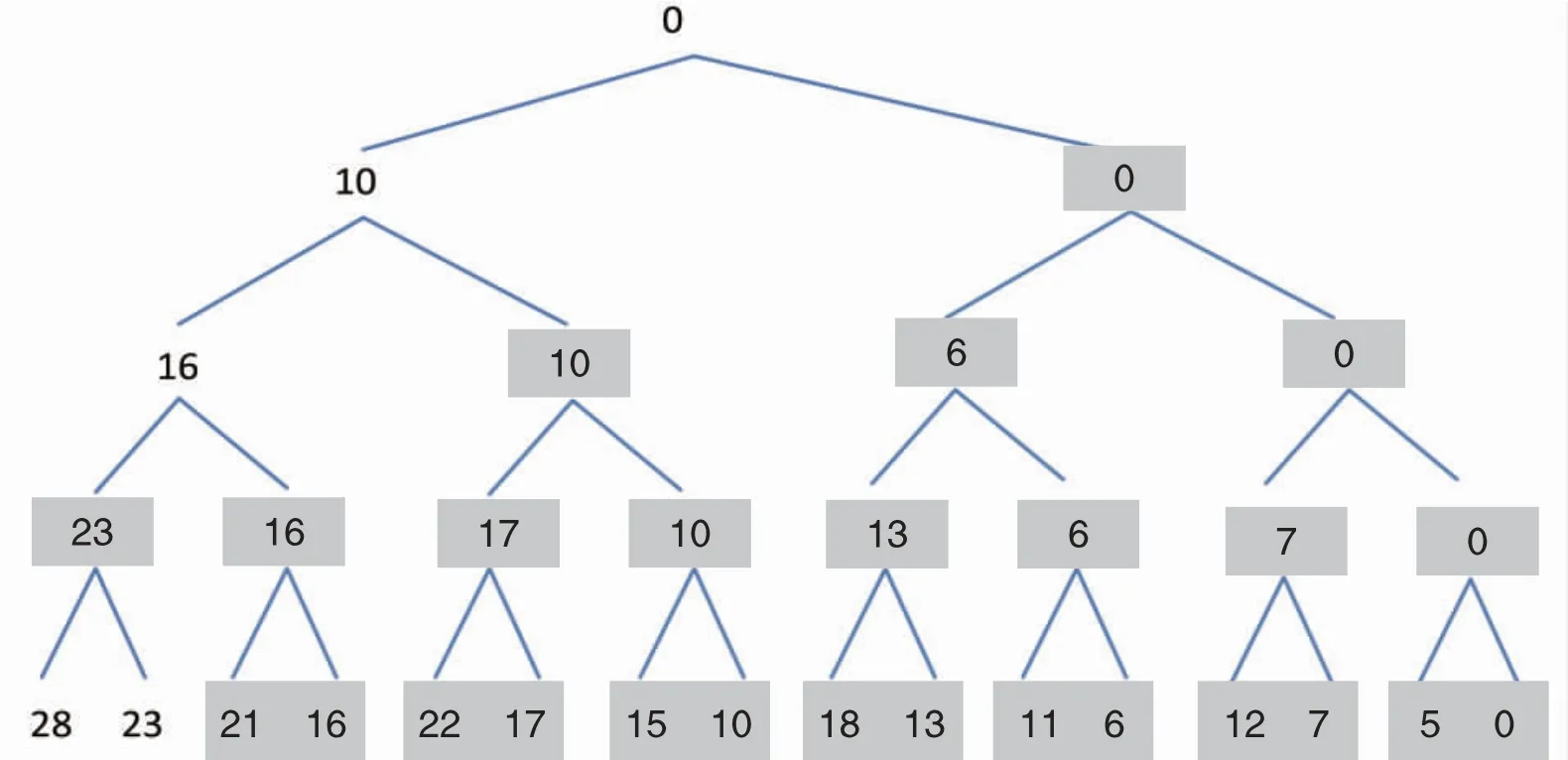
图1 子问题1解空间树

由贪心选择法（优先选择单位重量价值大的物品）得到的搜索下界为74，生成的搜索树见图2，优先选择限界函数值ub大的结点搜索，ub值小于74的结点剪枝。

图2 子问题1搜索树

由搜索树可得子问题1最优解背包价值为74，x1-x4取值1 100，即物品1装载，物品2装载，物品3不装载，物品4不装载。

2.2 算法描述EVAKNP算法子问题的求解采用堆存储搜索树中的结点，堆依据结点的限界函数值进行调整。首先生成并初始化根节点，取堆顶元素作为当前搜索结点，生成其左孩子结点（装载物品）及右孩子结点（不装载物品），分别计算限界值，将左、右孩子结点插入堆并进行堆调整。重复上述搜索过程直到当前搜索结点是搜索树的叶子结点。

EVAKNP（m，goos［m］［100］）

｛V=0；

while（i＜=m）

｛n=length（goods［i］）；//第i站物品数

newheap（n*n）；//申请堆空间

createrootnode（xnode）；//建立并初始化根节点

while（xnode＜n）//xnode不是搜索树中的叶子结点

｛createlchildnode（ynode）；//生成当前搜索结点的左孩子结点

bound（ynode）；//计算限界函数值

insert（heap，ynode）；//在堆中插入左孩子结点并调整堆

createrchildnode（znode）；//右孩子结点

bound（znode）；

insert（heap，znode）；

deltop（heap，xnode）；//取堆顶元素作为当前待搜索结点xnode

｝

vi=xnode→v；

V+=vi；i++；

｝

｝

void bound（KNAPNODE*node，int M，goods a

［］，int n）//计算结点node的限界函数值

｛int i=node-＞k；//计算i-1号物品装载情况的限界

float w=node-＞w；

float p=node-＞p；

if（node-＞w＞M）//物体重量超过背包载重量

node-＞b=0；

else

if（i＜n）

node-＞b=p+（M-w）*a［i］.p/a［i］.w；

else

node-＞b=p；

｝

3 算法分析及实验

分支限界法的实质是在解空间树中优先选择限界函数值大的结点进行搜索，由于解空间树的结点具有指数阶，在最坏情况下，算法时间复杂度为指数阶。在EVAKNP算法中，站点数记为m，各站点待装载物品最大数记为n，则算法在最坏情况下的时间复杂度为O（m2n），算法在最好情况下搜索过程持续沿一个分支往下进行，其时间复杂度为O（mn）。对于具体的问题实例，很难预测其搜索行为，无法判断能否在合理时间范围内求解，故很难估算EVAKNP算法在平均情况下的时间复杂度，可记为O（m2n）。由于解空间树中结点的搜索是跳跃性的，在每个结点中需存储从根节点到当前结点的搜索路径，算法还需要维护搜索树待处理结点表T，并且需要快速从表T中查找限界值大的结点，这些都增加了算法的空间耗费。最坏情况下，表T中结点数是指数阶的，故本算法的空间复杂性为指数阶。

实验数据集由随机合成，实验环境为Visual Studio 2012，编程采用C++语言。图3是站点数5，物品数分别为26、27、28、29、30的最优解。表1为站点数10，各站物品数均取10、15、20、25、30、35下算法运行时间比较，由表中数据可知在站点数相同的情况下，算法运行时间和物品数之间不构成函数关系，验证了分支限界法在最优解求解过程中搜索结点选择的不确定性。最优解的搜索过程往往与车辆容量、物品构成、物品数等均有关系，在车辆容量、站点数、物品数相同的情况下，物品构成不同，其搜索过程不同，算法运行时间也会不一样。表2是在站点数、车辆容量、物品数均一致（10站，车辆容量150，每站20个物品）算法5次运行时间比较，由于每次物品重量及价值随机生成，物品构成不同，算法运行时间均不同。

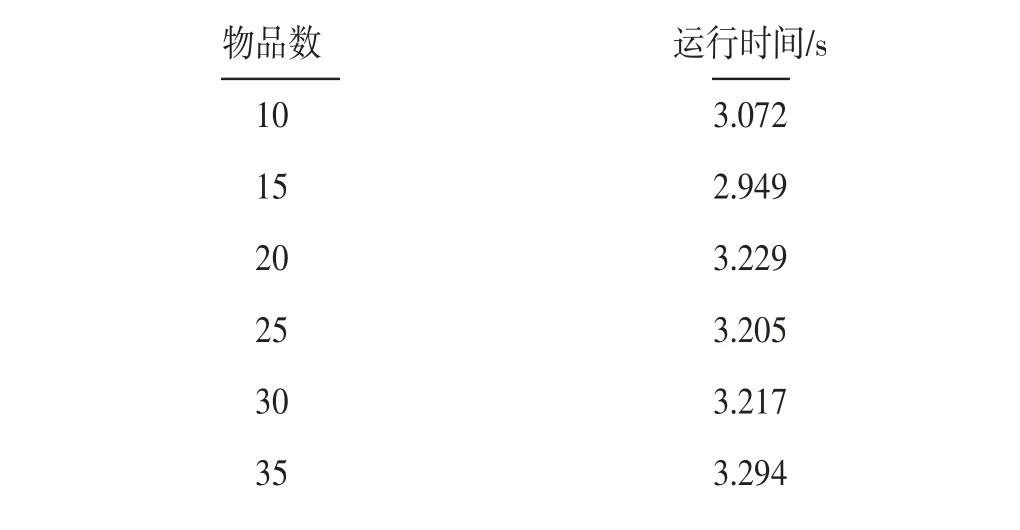
表1 不同数据规模EVAKNP算法时间性能

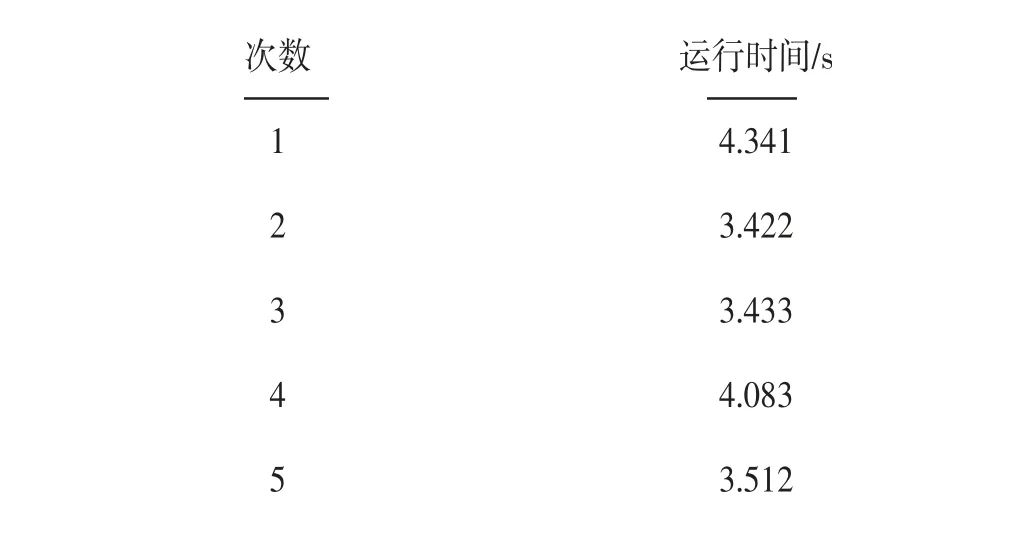
表2 相同数据规模EVAKNP算法时间性能

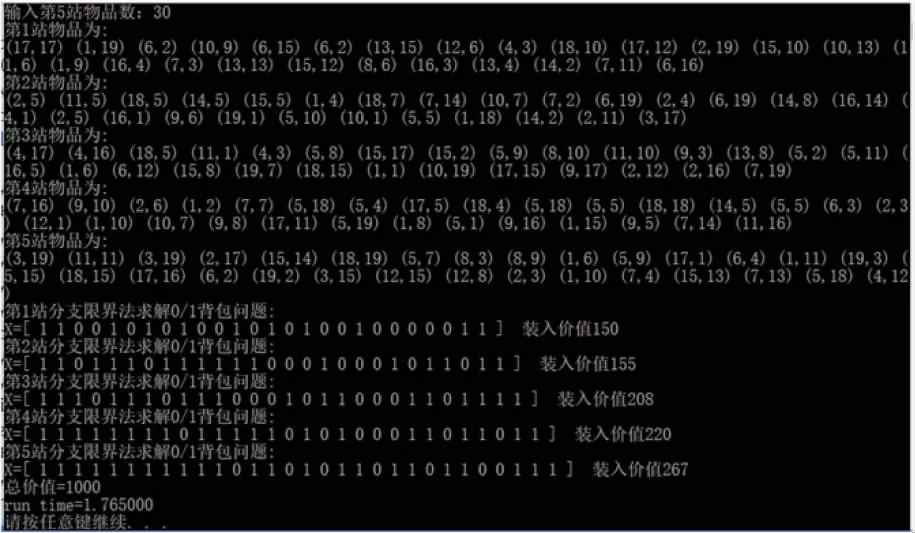
图3 EVAKNP问题最优解

4 结语

背包问题求解可采用蛮力法、贪心法、动态规划法、分支限界法等，蛮力法时间复杂度较高，贪心法可求近似最优解，动态规划法〔7〕和分支限界法求最优解。本文提出一个基于堆结构带限界函数的EVAKNP算法，实验结果表明该算法可以求解快递车辆配装问题最优解，算法在不同数据规模下具有有效的时间性能，由于分支限界法的搜索特点，算法在相同的数据规模、不同的数据集上具有不同的时间性能。