推导幂函数和指数函数的导数公式
◎樊贤泽
(石门县太平镇中心学校,湖南 石门 415328)
一、证n次幂差公式
指数相同的两幂差,在指数是大于等于2的整数情况下,有下面这个公式——n次幂差公式:
an-bn=(a-b)(an-1+an-2b+…+abn-2+bn-1).
当指数是不小于3的奇数时,此情形下的公式验证可以这样做.
如图1所示,令a>b>0,幂差a2k+3-b2k+3可认为是:从一个相邻边长为a2,a2k+1的矩形里截去一个相邻边长为b2,b2k+1的矩形后剩下部分的面积.

图1
则可得等式:
a2k+3-b2k+3=a2k+1(a2-b2)+b2(a2k+1-b2k+1).
不难验证,当k∈Z,k≥0,a,b∈R时,这个等式是成立的.
利用这个等式可得指数为不小于3的奇数的情形下的幂差公式.
将k=0代入等式计算:
a3-b3
=a(a2-b2)+b2(a-b)
=(a-b)(a2+ab+b2).
将k=1代入等式并利用k=0时的结论计算:
a5-b5
=a3(a2-b2)+b2(a3-b3)
=a3(a2-b2)+b2(a-b)(a2+ab+b2)
=(a-b)(a4+ab3+a2b2+ab3+b4).
将k=2代入等式并利用k=1时的结论计算:
a7-b7
=a5(a2-b2)+b2(a5-b5)
=a5(a2-b2)++b2(a-b)(a4+a3b+…+ab3+b4)
=(a-b)(a6+a5b+…+ab5+b6).
由此可推知:同指数且指数为奇数(不小于3)的幂差公式如下:
a2k+3-b2k+3=(a-b)(a2k+2+a2k+1b+…+ab2k+1+b2k+2).
指数是非2n的不小于6的偶数,可用奇指数的n次幂差公式证得偶指数的n次幂差公式.将非2n的不小于6的偶数记作2(2k+3)(k∈Z).
a2(2k+3)-b2(2k+3)
=(a2k+3+b2k+3)(a2k+3-b2k+3)
=(a-b)(a2k+3+b2k+3)(a2k+2+a2k+1b+…+ab2k+1+b2k+2).
因为a2k+3(a2k+2+a2k+1b+…+ab2k+1+b2k+2)=a4k+5+a4k+4b+…+a2k+4b2k+1+a2k+3b2k+2,
b2k+3(a2k+2+a2k+1b+…+ab2k+1+b2k+2)=a2k+2b2k+3+a2k+1b2k+4+…+ab4k+4+b4k+5,
所以a2(2k+3)-b2(2k+3)
=(a-b)(a2k+3+b2k+3)(a2k+2+a2k+1b+…+ab2k+1+b2k+2)
=(a-b)(a4k+5+a4k+4b+…+ab4k+4+b4k+5).
若指数是2k(k≥1),则n次幂差公式也适用.
a2-b2
=(a-b)(a+b).
a4-b4
=(a2-b2)(a2+b2)
=(a-b)(a+b)(a2+b2)
=(a-b)(a3+a2b+ab2+b3).
…
思路同前面所述的一样,用几何图形表示a2k+3+b2k+3(a>b>0)(如图2所示).

图2
构造下面这个等式,用它可证明指数为奇数情形时的n次幂和公式.
a2k+3+b2k+3
=a2(a2k+1+b2k+1)-b2k+1(a2-b2).
将k=0代入等式计算:
a3+b3
=a2(a+b)-b(a2-b2)
=a2(a+b)-b(a+b)(a-b)
=(a+b)(a2-ab+b2).
将k=1代入等式并利用k=0时的结论计算:
a5+b5
=a2(a3+b3)-b3(a2-b2)
=(a+b)(a2(a2-ab+b2)-b3(a-b))
=(a+b)(a4-a3b+a2b2-ab3+b4).
将k=2代入等式并利用k=1时的结论计算:
a7+b7
=(a+b)(a6-a5b+a4b2-a3b3+a2b4-ab5+b6).
…
a2k+3+b2k+3
=(a+b)(a2k+2-a2k+1b+a2kb2-…+a2b2k-ab2k+1+b2k+2).
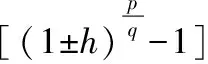




p,q为常量,根据幂函数的图像特征可得:
=p.
=q.




三、推导幂函数的导数公式
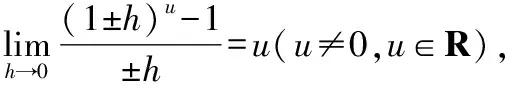
对于给定的x(x≠0),
利用此极限,根据导数的定义,可推导出实数范围内的形如f(x)=xu(x≠0,u≠0)的幂函数导数公式.若变量为0,则需另外讨论.过程看似与教材上的一样,但其涉及的极限的导出不同于教材.
f′(x)
=(xu)′
=uxu-1
=uxu-1.
幂函数f(x)=xu(x≠0,u≠0)的导数公式可记为:
f′(x)=(xu)′=uxu-1(u≠0,u∈R).
四、推导指数函数的导数公式

f′(x)
=(ax)′
=axlna.

