分布式可重入车间绿色共享制造与预维护联合优化*
董 君,毛 强
(河南工学院 管理学院,河南 新乡 453003)
0 引言
可重入混合流水车间(Re-entrant hybrid flow shop, RHFS)常见于半导体晶圆、印刷电路板、薄膜晶体管液晶显示器等高精电子制造产业中,是典型的NP-hard问题[1]。本文提出的分布式可重入车间绿色共享制造与预维护联合优化问题(Joint optimization of green shared manufacturing and preventive maintenance for distributed re-entrant workshop, GSMPM-DR)在RHFS基础上进行扩展,难度更大,复杂度更高,同样属于NP-hard问题。
1 GSMPM-DR问题描述
高精电子制造企业的设备一般较为昂贵,由于其对环境参数要求很高,所以工厂一经建立,设备基本全年全天不停歇运转。长时间的持续生产,机器会产生退化和遗忘效应[2]。因此,很有必要对设备进行预维护操作,以避免延长加工时间,并相应地减少机器能耗和碳排放,从而实现企业向绿色制造模式转变。本文研究中优化目标为最小化最大完工时间Cmax、最小化总碳排放TCT和最小化预维护成本Tcost。Cmax为最后一个工件的完工时间;TCT为绿色指标,本文仅考虑和工件调度相关的设备工作和空闲状态电能消耗产生的碳排放以及使用润滑油产生的碳排放。
2 改进的IHMMVO算法
2.1 IHMMVO算法流程
本文提出的IHMMVO算法在单目标多元宇宙优化(Multi-verse optimizer, MVO)[3]算法的基础上加入了快速非支配排序、拥挤距离计算、精英选择策略去解决多目标优化问题。此外,主要的改进策略有同步调度维护策略、初始化种群融合策略、宇宙个体位置信息扰动策略和NSGA-II变异策略,IHMMVO算法流程如图2所示。
2.2 初始化子种群融合策略
为了扩大种群的多样性,本文将两个子种群融合后筛选出一个更优的初始种群。两个子种群具有相同的规模N,其中子种群pop1个体的位置变量随机生成,子种群pop2个体的位置变量是在pop1个体位置的基础上进行差分进化变异操作后生成的。依次随机从pop1个体中选取3个个体,进行变异形成pop2中个体的位置变量。将子种群pop1和pop2合并并进行拥挤距离的计算和快速非支配排序,得到非劣解集组成的初始外部档案Archive。将整个种群分成两个规模相同的子种群popx和popy。两个子种群执行不同的进化策略,对popx中的宇宙个体执行莱维飞行扰动变异操作,对popy中的宇宙个体执行NSGA-II操作,以扩大种群多样性和搜索范围。
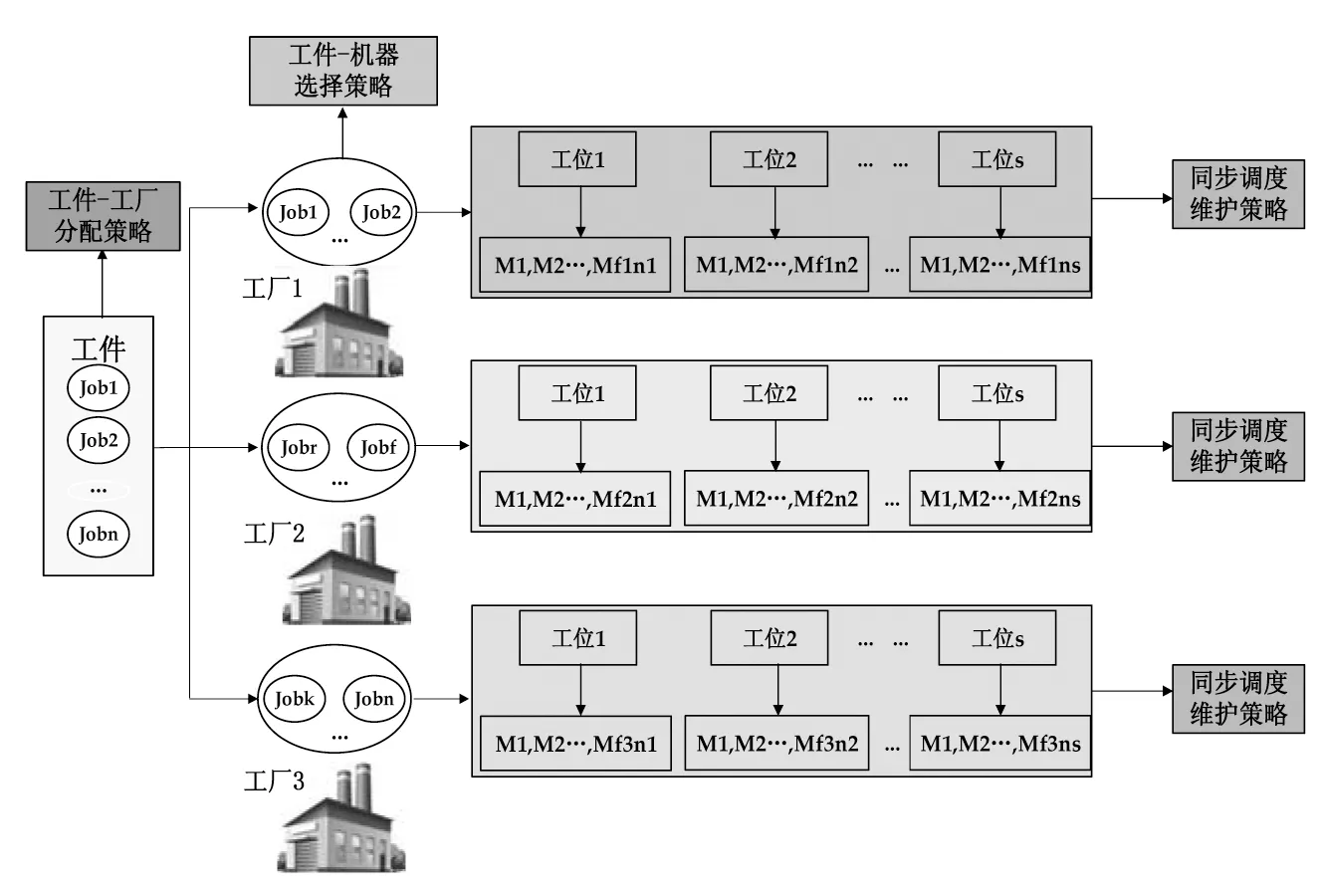
图1 GSMPM-DR问题示意图

图2 IHMMVO算法流程图
2.3 宇宙个体位置信息扰动策略
本文引入莱维飞行扰动策略,对迭代前期宇宙个体的位置信息进行扰动,以增加种群多样性,并得到新的宇宙子代种群C1。个体位置信息变化公式为[4]:
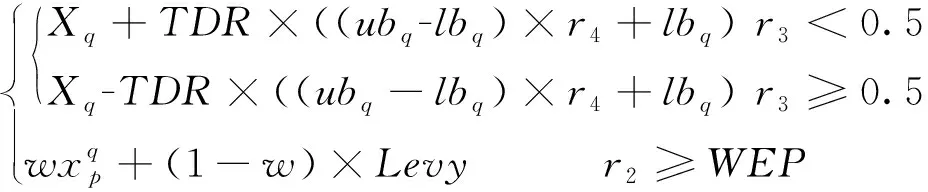
(1)
w=wmax-(wmax-wmin×(l/L)2
(2)
其中:w是加权学习因子;Levy是Lévy飞行步长。
2.4 NSGA-II变异策略
策略1 对每一个工厂内工件加工顺序重新进行随机排列,以扩大整个种群个体的多样性。
策略2 根据随机数rand取值,若rand<1/3,则针对Cmax指标进行操作;若0 为了验证IHMMVO算法求解GSMPM-DR的有效性,实验阶段选取MMVO、IMSSA[5]和MOPSO算法[6]进行比较。实验阶段,为了使三个目标函数值处于相同的数量级,对其进行min-max归一化处理。 因为公开的文献中没有求解GSMPM-DR问题的数据集,本文参考文献[7]中的数据集设置方法,生成测试算例。数据集中包括2个工厂数标准(2/3)、3个工件数标准(20/60/100)、2个加工层次标准(U[2,3]/U[3,4])、3个工位数标准(U[2,4]/U[5,7]/U[8,10])、2个机器数标准([工件数/10]+1或+2)。共有2×3×2×3×2=72个参数组合。对于每个参数组合随机生成10个测试算例,共包含72*10=720个测试算例。例如20l1g1-m代表工件数为20,加工层次为U[2,3],工位数为U[2,4],机器数随机为3或4的测试算例。数据集中涉及的参数及其取值参见文献[4]。 因篇幅有限,本文仅列出了工厂数为3时IHMMVO和MMVO、IMSSA、MOPSO四个算法之间的实验结果对比,如表1所示。可以看出,针对SP指标,IHMMVO算法的占优率为66%,MMVO、IMSSA和MOPSO算法的分别为11%、6%和17%;针对GD和IGD指标,IHMMVO算法的占优率均为100%。表1还展示了威尔科克森(Wilcoxon)符号秩检验结果,分别用‘+’、‘=’和‘++’符号进行表示,对比不同算法之间是否存在显著性差异。‘+’代表IHMMVO算法显著优于对比算法,‘=’代表两种对比算法之间没有明显区别,‘++’代表IHMMVO显著劣于对比算法。针对所有优化指标,相比其余算法,IHMMVO对于大部分测试算例均能够实现显著占优,说明其获得的Pareto解集均匀性、多样性以及收敛性优势明显,同时该结论通过图3的三个评价指标箱线图进一步得到了验证。 表1 IHMMVO、MMVO、IMSSA、MOPSO算法实验结果对比 图3 评价指标箱线图 (1) 图4分别展示了2*60*[2,3]*[8,10](2个工厂、60个工件、加工层次在[2,3]中随机选取、加工工位在[8,10]之间随机选取)和3*20*[2,3]*[5,7]算例各个算法获得的Pareto前沿对比图。可以明显看出,IHMMVO算法获得的Pareto前沿位于其余三种对比算法获得的Pareto前沿的下方,更加接近真实的Pareto前沿。 (a) 2*60*[2,3]*[8,10] (b) 3*20*[2,3]*[5,7]图4 各个算法获得的Pareto前沿对比图 (2) 根据Hewlett Packard公司晶圆生产技术开发实验室半导体生产线构建的HP24模型,大部分参数均来自实际设备采集的数据[8]193-194。该模型共包含24个设备群组,共27台设备。图5为HP24模型产品加工流程,其具体参数参见文献[8]。因HP24模型只考虑一种产品的加工,所有产品加工时间、PM时间、设备维修间隔时间均相同,无需考虑各个工件的加工顺序优化问题,因此本文在工厂数为2、工件数为20的情况下,考虑不同的工件分配方案对优化目标的影响,实验结果如表2所示。结果显示,针对HP24模型,对于该测试算例,当每个工厂各分配10个工件时,获得的makespan、总PM成本和总碳排放均能够达到最小值,且三个优化指标的变化趋势基本相同。 图5 HP24模型产品加工流程 表2 不同工件分配方案对比 本文针对半导体晶圆分布式绿色共享制造与预维护联合优化问题,考虑了多工厂分布式制造模式和设备预维护的联合优化,能够提高生产效率、缓解机器退化和遗忘效应导致的加工时间延长、生产能耗增加的现象。通过仿真实验验证了所提出的IHMMVO算法能够跳出局部最优值,对于求解该问题具有可行性和竞争力。算法获得的Pareto前沿解集可以帮助决策者根据实际运营情况,从中选择一个较优的调度方案。此外通过对半导体生产线HP24模型的实验,验证了在半导体晶圆制造企业应用分布式制造模式对于优化生产效益、经济利益和绿色指标的有效性,证明了本文的实际应用价值和借鉴意义。3 仿真实验
3.1 测试算例和参数设置
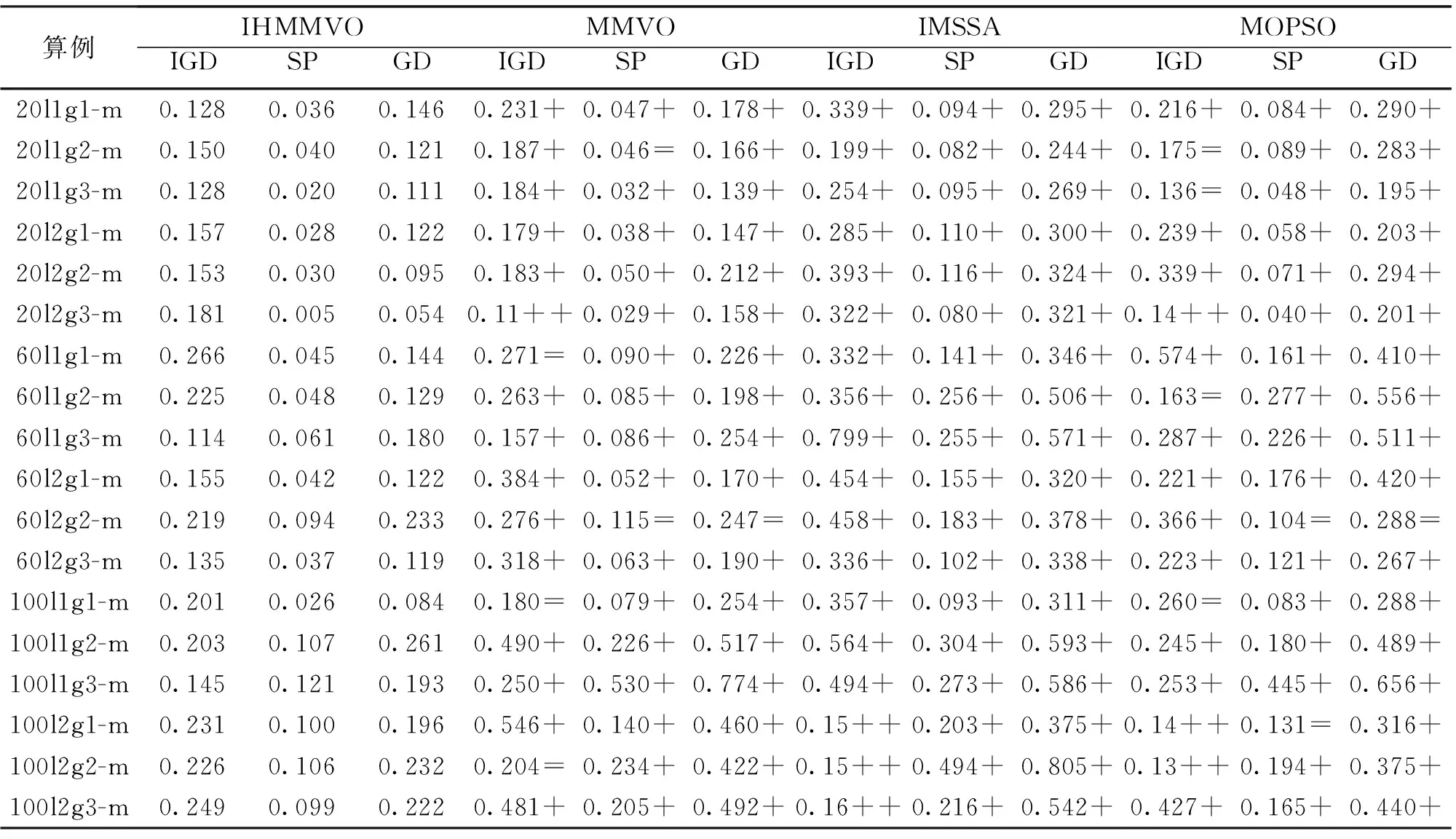
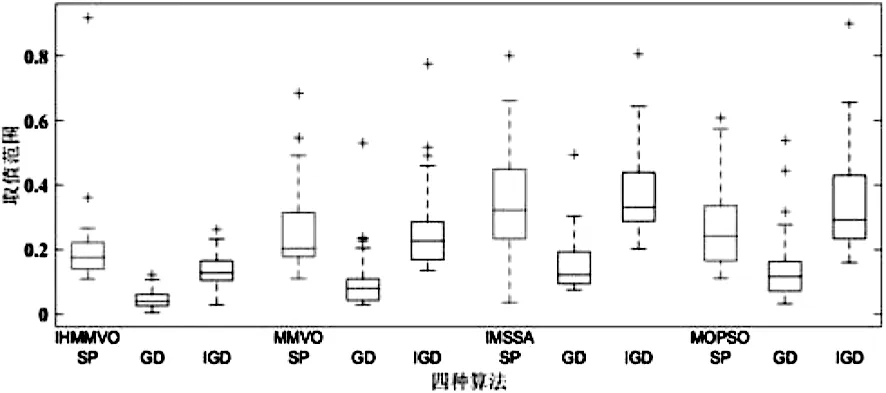
3.2 算法性能测试和结果分析
3.3 案例分析



4 结论

