多维能量熵在滚动轴承故障诊断中的应用*
李 婕,胡永涛,李 昊,赵 斌
(1.河南工学院 电气工程与自动化学院,河南 新乡 453003;2.新乡市旋转机械运行状态智能监测工程技术研究中心, 河南 新乡 453003)
0 引言
滚动轴承是风机、电机、减速机、齿轮箱等旋转机械设备中用量较大的零件之一[1]。由于转速、负载等运行工况经常变化,加之工作环境恶劣,滚动轴承极易发生磨损、脱落、裂纹、变形等故障,从而诱发旋转机械故障,甚至引发生产安全事故[2]。因此,研究滚动轴承故障诊断的新理论和新方法具有重大意义。
振动信号包含了大量能反映滚动轴承运行状态的信息,并且通过振动传感器和信号采集仪可以方便地获得滚动轴承振动信号,因此,通过一定的处理方法对滚动轴承振动信号进行分析和处理,获取能够反映滚动轴承运行状况的显著信息可以进行故障诊断。小波变换是最早用于时频域分析的一种方法,基于小波变换及其改进方法的滚动轴承故障特征提取被广泛用于滚动轴承故障诊断[3]。然而,小波变换存在固有缺陷,如频率混叠、方向性差、平移敏感等,此外小波参数选择复杂,不同参数对小波变换的有效性影响较大,这导致小波变换难以在滚动轴承故障诊断工程应用中取得良好的诊断结果[4]。复小波变换具有抑制频率混叠、方向可选择、平移不变、高效计算能力等优点,逐渐成为信号处理领域的研究热点[5]。
模式识别是采用分类算法,根据能够反映滚动轴承运行状况的显著信息把不同状态的滚动轴承进行分类[6]。目前,大部分研究采用深度神经网络进行故障识别,但深度学习神经网络是一种有监督学习方式,其训练需要大量有标签样本,而在实际工程中很难取得所有故障类型的样本数据,导致其难以应用。模糊C均值(Fuzzy C-Means, FCM)采用无监督学习方式,可以根据振动信号的相似性对滚动轴承进行分类,只需要知道所有滚动轴承状况类别总数即可,不需要知道每个滚动轴承具体属于哪一类,具有算法简单、准确率高、易实施等优点,可以很好地实现滚动轴承故障诊断。
本文提出一种多维能量熵的滚动轴承振动信号处理方法,以提取滚动轴承的故障特征,并用于滚动轴承故障的诊断。首先提出多维能量熵的概念,然后给出一种基于双树复小波变换(Dual-Tree Complex Wavelet Transform, DTCWT)的多维能量熵获取方法,最后借助FCM聚类构建滚动轴承故障诊断模型,并搭建滚动轴承故障模拟实验系统加以验证。
1 基于DTCWT的多维能量熵特征提取
1.1 多维能量熵
机械设备运行时,正常滚动轴承振动信号的能量随机分布,当滚动轴承发生故障时,振动信号中包含大量谐波,能量向谐波集中,降低了随机性,因此能量分布可以一定程度上反映滚动轴承的运行状态。然而因能量分布鲁棒性较差,当生产现场存在大量噪声时,能量分布受噪声影响较大,导致能量分布不能正确反映滚动轴承的运行状态。Shannon在1948年首次提出熵的概念,熵采用信息的概率期望反映信息分布的随机性[7],具有较好的抗噪性能。将能量通过概率期望的方式进行表示,可以避免噪声对能量分布的影响,因此本文定义能量熵,并将其作为滚动轴承的故障特征。
设离散随机变量Y∈{y1,y2,…,yk},定义其熵为EP(Y)
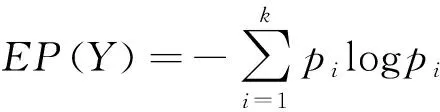
(1)
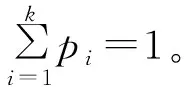
滚动轴承振动信号包含了大量不同的频率成分,可通过时频域分析将其分离为m个包含不同频率成分的分量,每个分量包含n个数据点。定义第i个分量的能量为Ei:
(2)
其中aij为第i个分量中第j个数据点的值,则第i个分量的能量分布概率为:
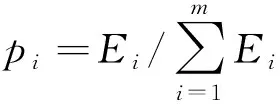
(3)
将公式(2)和公式(3)带入公式(1)得到振动信号的一维能量熵:
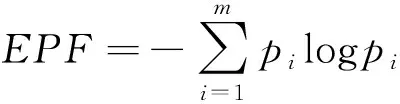
(4)
一维能量熵是所有分量能量分布的概率表示,反映了滚动轴承振动信号能量的全局分布情况,不同状态滚动轴承的振动信号包含的谐波不同,因此其能量整体分布存在差异,一维能量熵也不一样。
此外,滚动轴承运行在故障状态时,不同分量的局部能量分布不一样,因此,可定义第i个分量的能量熵,即i维能量熵。
定义第i个分量的第j个采样点的局部能量为Eij:
Eij=|aij|2
(5)
则第i个分量的第j个采样点的局部能量分布概率为pij:
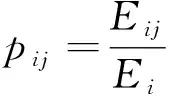
(6)
将公式(5)和公式(6)代入公式(1),得到i维能量熵:
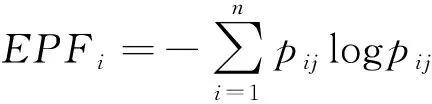
(7)
i维能量熵是某一分量的局部能量的概率表示,反映了滚动轴承振动信号中不同分量的局部能量分布情况,由于不同分量的能量分布不一样,i维能量熵也存在差异。
综上所述,一维能量熵与i维能量熵能够从全局和局部多个维度反映滚动轴承振动信号的能量分布情况,可以很好地表征滚动轴承的运行状态,将其作为故障特征能够有效提高故障诊断的准确率。
1.2 DTCWT信号分离
为了获取多维能量熵,需将滚动轴承振动信号分离为包含不同频率成分的多个分量。DTCWT是一种先进的时频分析方法,具有信号分离能力强、平移不敏感、算法简单等优点[8],可快速实现振动信号分解。下面以两层分解为例,说明DTCWT信号分离原理,DTCWT两层分解过程如图1所示,DTCWT由实离散小波和虚离散小波两部分构成[9]。
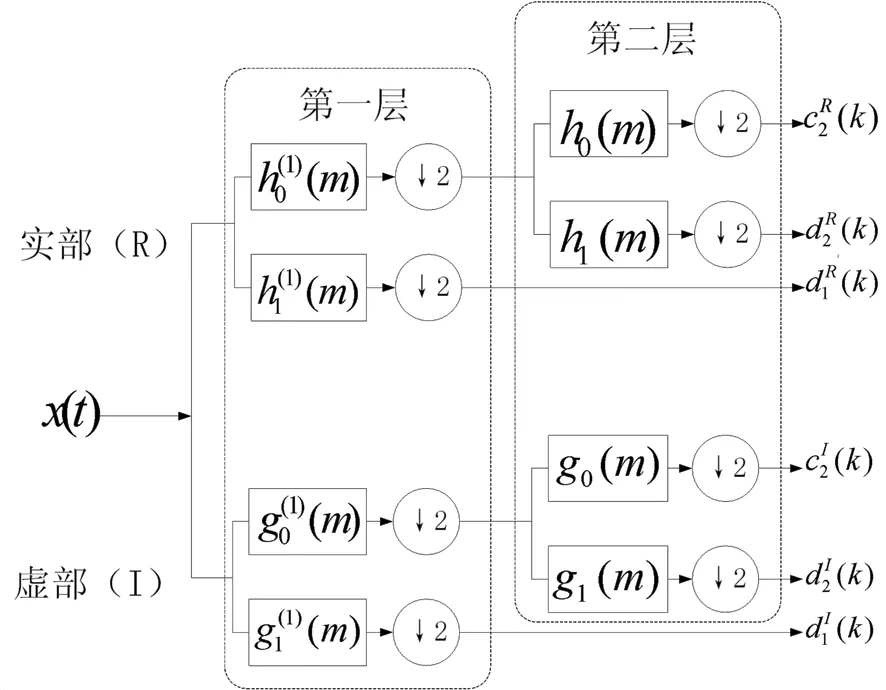
图1 DTCWT两层分解过程
假设实离散小波为Φh(t),虚离散小波为Φg(t),组合实离散小波和虚离散小波可得双树复小波ΦC(t):
ΦC(t)=Φh(t)+jΦg(t)
(8)
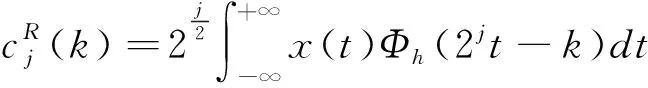
(9)
(10)
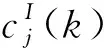
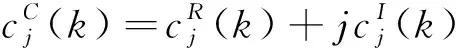
(11)
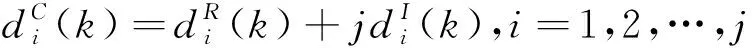
(12)
对尺度系数和小波系数进行逆变换即可将振动信号分离为3个频率成分由低到高的不同分量。
2 模糊C均值聚类
聚类分析是根据样本数据的相近程度,将相似样本聚为一类,实现样本不同类别的划分[12]。为了把具有m个振动信号的样本集X={x1,…xm}根据滚动轴承状态分为n类,假设聚类中心为V=[v1,v2,…,vn]T,计算样本xi到vj的欧几里得距离dij=‖xi-vj‖,定义样本隶属度矩阵为Um×n=[uij]m×n,uij∈[0,1]为xi属于类别j的模糊隶属度,定义目标函数为:
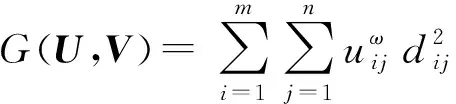
(13)
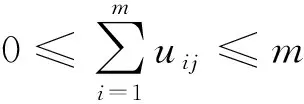
(1) 确定类别数n,初始化模糊隶属度权重ω、阈值ε、分类矩阵U=[μjk]n×m和迭代次数。
(2) 更新所有样本的聚类中心:
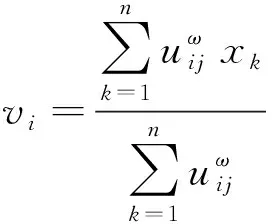
(14)
(3) 更新分类矩阵Um×n:
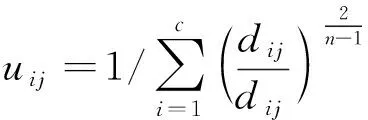
(15)
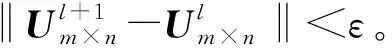
为了定量评价聚类性能,定义平均模糊熵HA和分类系数HC:
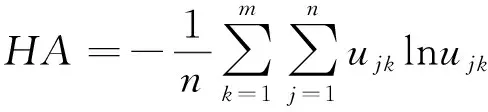
(16)
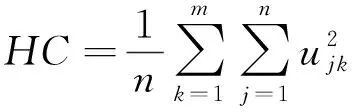
(17)
HA值越小,HC值越大,聚类性能越好。
3 滚动轴承故障诊断模型
基于上述研究,构建基于多维能量熵及FCM的滚动轴承故障诊断模型,如图2所示,具体操作步骤如下:
(1)信号获取:利用振动传感器及配套的信号分析仪获取滚动轴承振动信号。
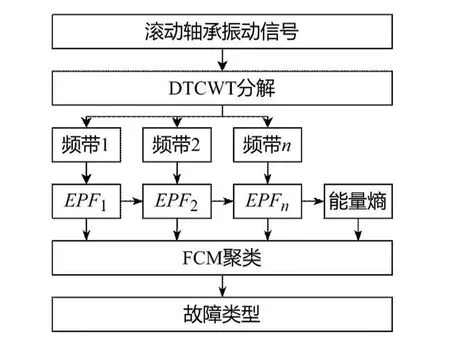
图2 滚动轴承故障诊断模型
(2)DTCWT分解:用DTCWT变换及反变换对振动信号进行处理,得到n个不同分量信号。
(3)多维能量熵:分别根据公式(4)和公式(7)计算一维能量熵和n维能量熵。
(4)FCM聚类:对一维能量熵和n维能量熵进行归一化处理,将其作为FCM的输入,对滚动轴承进行聚类。
(5)定性定量分析聚类效果,根据聚类结果判断滚动轴承故障。
4 实验分析
为了验证多维能量熵及滚动轴承故障诊断模型的有效性,搭建滚动轴承故障模拟实验系统,如图3所示,系统主要由MCDS机械故障模拟实验台、MI-7008数据分析仪、垂直固定于滚动轴承座上方的振动传感器和PC构成。其中MCDS机械故障模拟实验台由驱动电机、联轴器、转子、负载等部分构成,测试滚动轴承型号为ER-12K,测试滚动轴承具体参数如表1所列,通过滚动轴承座安装于负载端。

表1 测试滚动轴承具体参数
测试滚动轴承包括正常、内圈损伤、滚动体损伤及外圈损伤共4种不同状态,各个状态分别采集50次振动信号,共计200个振动信号,采样频率为12kHz,采样点数12,000,滚动轴承转速1800rpm,转频30Hz,负载20Nm。

图3 滚动轴承故障模拟实验系统
对所有振动信号进行2层DTCWT变换及反变换后,得到3个分量,提取各分量多维能量熵并进行归一化处理后作为故障特征。图4为不同状态滚动轴承振动信号的多维能量熵,EPF1、EPF2和EPF3分别为一维、二维和三维能量熵,由图4可以直观地看出同一状态的不同维度的能量熵存在差异,不同状态的对应维能量熵不同,因此EPF1、EPF2和EPF3可以作为滚动轴承故障特征,用于故障模式识别。
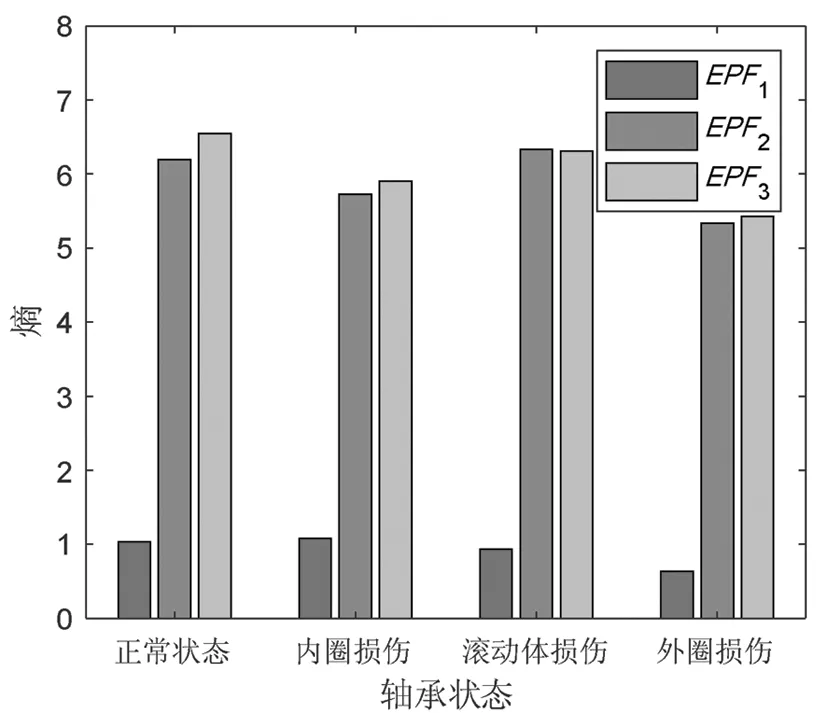
图4 四种状态滚动轴承振动信号的多维能量熵
利用多维能量熵作为FCM的输入,对200个振动信号进行聚类分析,四种状态滚动轴承振动信号的的聚类中心分别为[0.9279,0.9902,0.6362]、[0.5724,0.5636,0.1349]、[0.9597,0.8521,0.5429]和[0.7219,0.7228,0.6947]。聚类结果如图5和图6所示,图5为不同状态滚动轴承FCM聚类的三维图,图6为不同状态滚动轴承FCM聚类的等高线,综合图5和图6可以明显地看到四种状态滚动轴承的50个样本紧密围绕各自的聚类中心,任何一个样本只属于某一类,分类系数HC=0.9042,平均模糊熵HA=0.3018,表明200个滚动轴承样本被准确地分成了4类,分类准确率如表2所列,故障模式识别准确率达到100%。
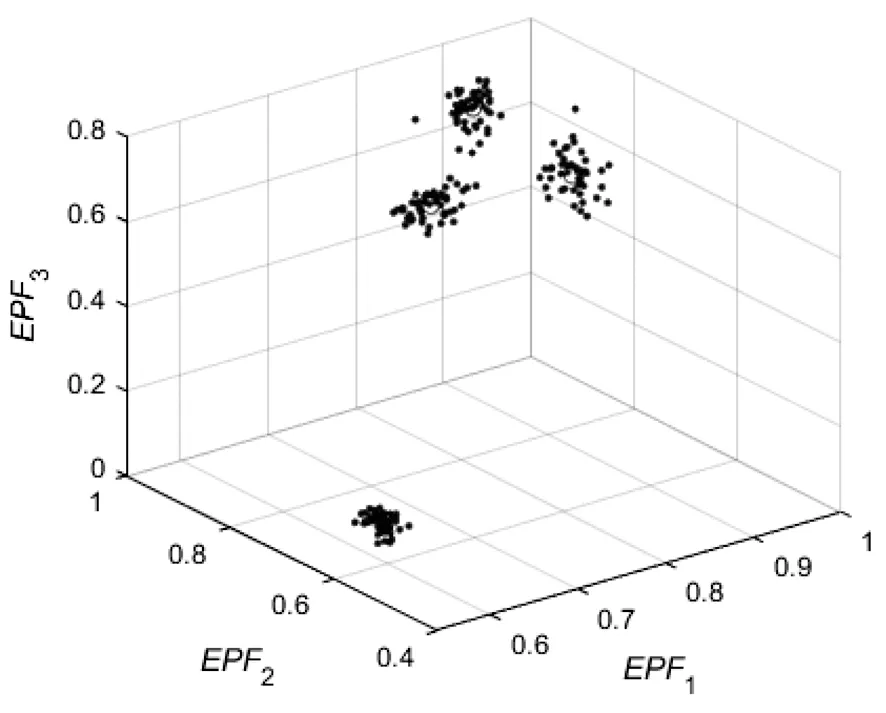
图5 不同状态滚动轴承FCM聚类的三维图

图6 不同状态滚动轴承FCM聚类的等高线

表2 四种状态分类准确率
5 结束语
本文提出了一种多维能量熵的特征提取方法,结合FCM构建了滚动轴承故障诊断模型,并搭建了滚动轴承故障模拟实验系统对所提方法及模型进行了实验分析。实验分析结果表明,多维能量熵能够从全局和局部反映滚动轴承运行状态,结合FCM聚类分析能够快速识别滚动轴承故障,所提故障诊断模型具有算法简单、准确率高的优点,方便作为分析程序部署在服务器进行故障诊断分析,可实现滚动轴承运行状况的远程监测。限于当前的实验条件,本文未对其复合故障及保持架故障进行研究。然而,无论是复合故障还是保持架故障,在同等工况下,其振动信号必然存在差异,因此,采用多维能量熵作为故障特征,结合FCM聚类分析也能够实现对故障类型的准确识别。后续将针对复合故障诊断和保持架故障诊断开展专门研究。

