基于克兰机构的八足机器人仿真分析*

康玉辉,陈荣尚,吴豪琼

(河南工学院 机械工程学院,河南 新乡 453003)

0 引言

机械仿生学早在20世纪60年代就开始受到人们的重视,机构和仿生学的结合给机器人设计提供了更多的可能性。多足机器人凭借较强的适应性和负载能力,已成为国内外研究的热点[1]。多足机器人多自由度的关节结构使得机器人腿部非常灵巧,但同时也使机器人的控制变得异常复杂,导致可靠性较低[2]。为此,本文提出了一种基于克兰机构的八足机器人,其左右两侧各有四个并联的克兰机构,使用两个电机实现前进、后退、转向等动作,且承载能力强、动静态稳定性好。

1 八足机器人的设计方案

1.1 行走机构布局及克兰机构

机器人躯干为长方体结构,八条腿在左右两侧,前后对称分布。这种分布方式使得机器人着地点始终在最外侧,可以有效提高稳定性。八足位置分布如图1所示,左侧四腿1、2、5、6由一个电机通过齿轮驱动,腿1、2安装在同一根轴上、相位差180°,腿5、6安装在同一根轴上、相位差180°,腿3、4、7、8同理。两侧两个电机同步同向运转时,腿1、4、5、8相位相同且同步,腿2、3、6、7相位相同且同步。机器人通过两侧电机的同步正反转实现前进和后退动作,通过异步正反转实现转向动作。

图1 机器八足位置分布

机器人腿采用克兰机构,克兰机构是平面6杆机构,如图2所示。克兰机构由机架(三副杆)、4个二副杆和1个三副杆组成。AB为原动件,H点为行走机构末端。

克兰机构控制简单,通过调节参数,H点可实现复杂轨迹,作为机器人的腿部结构较为合适。

以铰链中心A为原点,建立直角坐标系AXZ,做矢量多边形,如图 2 所示。

图2 克兰机构原理图

依据四边形ABDC,得到复数矢量方程

l1eiθ1+l2eiθ2=l3eiθ3+l4eiδ

(1)

根据欧拉公式展开,实部虚部分离可得到

l1sinθ1+l2sinθ2=l3sinθ2+l4sinδ

(2)

l1cosθ1+l2cosθ2=l3cosθ2+l4cosδ

(3)

依据五边形CEFGD,得到复数矢量方程

(4)

根据欧拉公式展开,实部虚部分离可得到

(5)

(6)

看作由E点出发的向量,H点位置可表示为:

(7)

(8)

看作由A点出发的向量,H点位置可表示为:

(9)

(10)

以上格式中各杆长度为已知量,θ1也为已知量δ,β为常量,由式(2)、(3)、含θ1的项右移,两边平方再对应相加得到

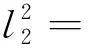
(l3cosθ3+l4cosδ-l1cosθ1)2

(11)

整理得

2l3(l2sinδ-l1sinθ1)sinθ3+

2l3(l3cosδ-l1cosθ1)cosθ3+

2l1l4cosθ1cosδ=0

(12)

令A=2l3(l4sinδ-l1sinθ1)

B=l3(l4cosδ-l1cosθ)

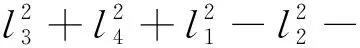
2l1l4sinθ1sinδ-2l1l4cosθ1cosδ

则式(12)可简化为

Asinθ3+2Bcosθ3+C=0

解得

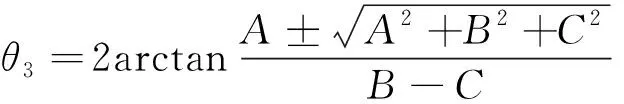
(13)

同理可求得θ2、θ5、θ6关于θ1的表达式，带入(7)、(8)或(9)、(10)即可得到H点位置表达式。

1.2 克兰机构的运动轨迹仿真分析

初步确定克兰机构参数，建立克兰机构的三维模型，其初始数值见表1。将模型导入ADAMS添加约束和运动，运行仿真可测得末端轨迹如图3虚线所示，底部倾斜，跨距较小。经反复调整参数，获得较理想轨迹如图3实线所示，跨高约60mm，跨距约80mm，支撑段较平缓，可有效保证机器人的通过性和平稳性[3]。克兰机构的最终数值如表1所示。将参数代入H点位置表达式，通过Matlab绘制H点轨迹如图4所示，由图可知ADAMS仿真结果与Matlab计算结果一致。

表1 克兰机构尺寸

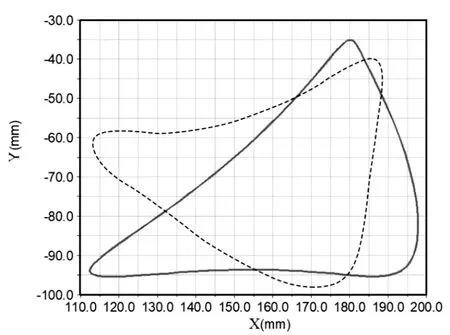
图3 克兰机构末端轨迹

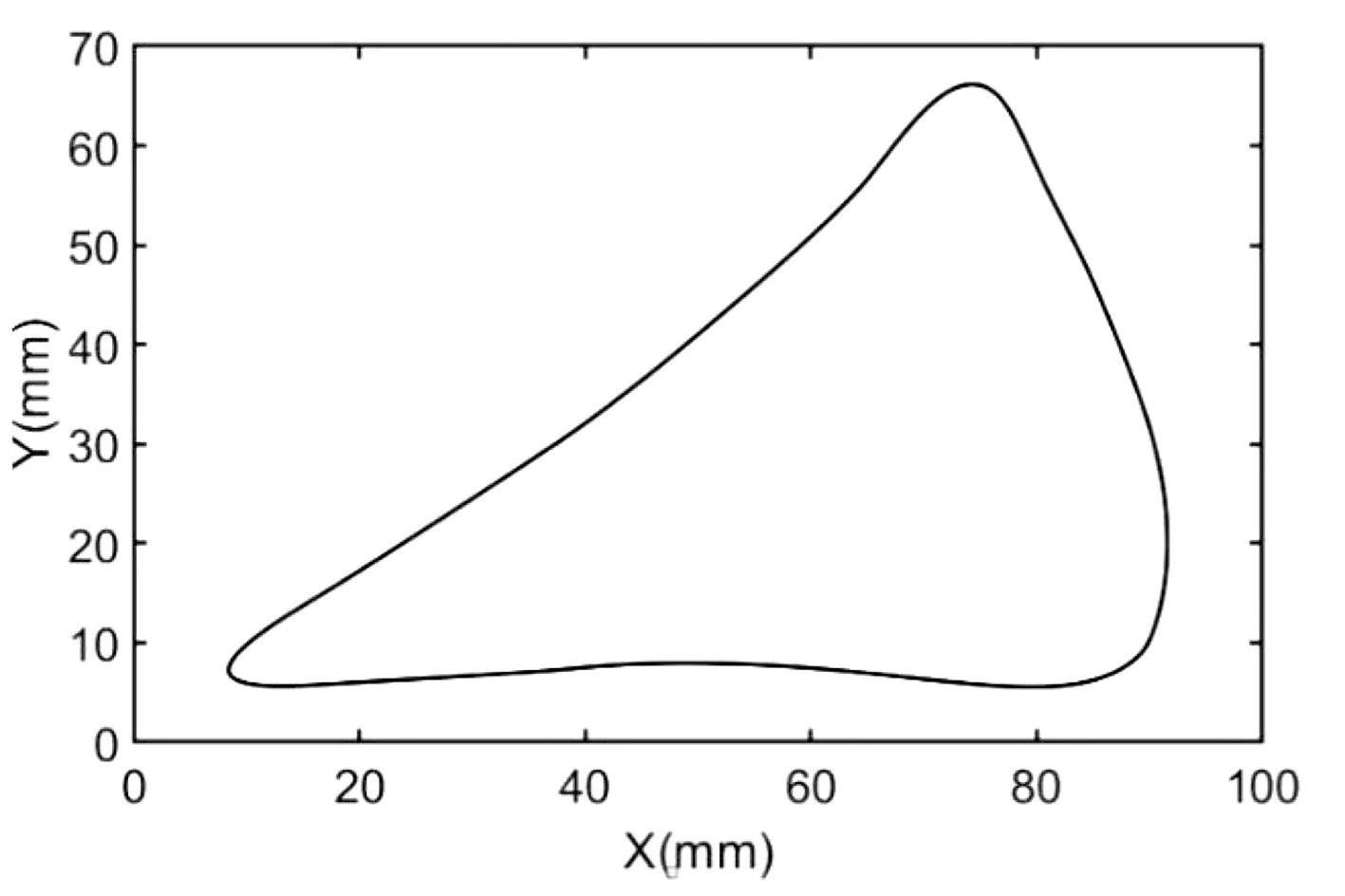
图4 Matlab绘制克兰机构轨迹

1.3 机器人总体结构

依据前文中机器人的腿部布局和克兰机构参数绘制机器人三维模型。机器人整体采用对称结构，每一侧由两块亚克力板通过螺栓固定，中间齿轮传动，两边安装行走机构。机架上安装四轴机械手，以完成抓取作业。整体三维模型如图5所示。

2 机器人仿真分析

因为软件与软件之间文件的传输容易失败，且在ADAMS中编辑三维模型不如通用三维软件方便[4]，所以将机器人三维模型进行简化。首先删除不必要的零件，其次尽量合并没有相对运动的零件，以保证导入成功，并减少在ADAMS中的编辑操作。简化后的模型如图6所示，将其导入 ADAMS，添加运动副[5]，设置接触关系和驱动，做好仿真准备工作。

2.1 直行仿真分析

设置驱动速度2r/s，时间3s，进行机器人直行仿真。机器人中心位移和速度如图7所示，实线表示机器人位移对应左侧纵坐标，虚线表示机器人速度对应右侧纵坐标。由图可计算出机器人平均速度为0.3m/s，根据驱动速度确定驱动电机参数进而确定齿轮传动比。由于输入的是匀速转动，机器人八足交替迈进，因此机器人的速度存在较大波动；如对速度变化有特殊要求，可以考虑变速输入。

图7 机器人位移和速度

机器人中心高度变化和中心偏移如图8所示。顶部虚线表示机器人中心与行驶方向的偏移情况，机器人始终保持直行，但存在周期性偏移，偏移最大数值小于2mm。底部实线为机器人中心高度变化情况，变化轨迹与机器人周期性的抬腿相符，变化幅度约5mm，行进过程中机器人本体较稳定，进一步证明克兰机构的参数选择较为合理。由于机器人中心位置与空间坐标系原点不重合，因此图中初始位置不为零。

图8 机器人中心高度变化和中心偏移

2.2 转弯仿真分析

设置驱动速度2r/s，时间3s，运行机器人转弯仿真。机器人完成了约150°的转向，如图9中虚线所示，右侧纵坐标对应转弯角度。转弯过程中机器人在水平面内X方向的位移如图9上部曲线所示，Y方向的位移如图9下部曲线所示，由于机器人中心位置与空间坐标系原点不重合，因此图中初始位置不为零，坐标系方向见图5。由图可见在转弯过程中机器人中心位置会存在小的偏移，但总体上比较稳定。

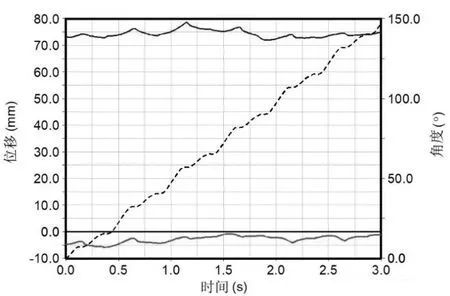
图9 转弯过程中机器人中心位移

3 机器人样机测试与分析

机器人腿和躯干采用亚克力板激光切割后拼接而成，传动齿轮和机械手部分采用PLA材料3D打印而成，主控模块采用Arduino UNO板，装配完成后如图10所示。对机器人进行直行、转弯测试：直行测试过程中会发生偏移，偏移量与仿真结果一致，见图11；原地左转弯测试中也发生偏移， 偏移量与仿真结果一致；行进中转弯测试中，由图12可见转弯存在滞后现象，主要原因是机器人腿末端与地面摩擦力较小[6]，后期可通过改变机器人腿末端结构和调整转弯控制程序进行改善。

图10 八足机器人实物图

图11 直行测试机器人中心偏移

图12 转弯测试机器人中心变化

4 结语

以机械仿生学为基础设计的八足机器人凭借较少的驱动实现了灵活运动，且稳定性强，能耗少，控制难度低。对原型机构的设计计算、仿真分析，为机器人的整体设计提供了理论支撑；对机器人整体机构的仿真分析证明了设计方案的可行性；对样机的测试，证明基于克兰机构的八足机器人具有控制简单和运动稳定的特点。