电动汽车长途出行路径引导方法

刘 珊，李建贵，李 强，朱郭福，陈 晨

(武汉理工大学 机电工程学院，湖北 武汉 430070)

由于电动汽车单次充电后续航里程较燃油车短，电动汽车长途出行难正成为电动汽车领域的一大难题。虽然效率在逐步提升但电动汽车充电过程与燃油车加油过程相比持续时间仍然较长。另外由于电动汽车充电站与充电桩建设速度较慢，电动汽车数量与充电站及充电桩数量不匹配，电动车充电时往往需要排队等待[1-2]。以上构成了电动汽车在长途出行时面临的主要问题为：续航里程短、充电时间长、需要排队等待。目前已有不少学者对电动汽车出行进行了研究。文献[3]对现有的电动汽车充电引导调度进行了总结，从用户最优与电网最优两方面对目前现有的电动汽车出行引导策略进行了探讨，认为用户最优的引导策略更符合当前的用户及市场需求。文献[4]构建了时空图谱注意力网络，通过分析电动汽车充电需求及交通网络数据对电动汽车出行需求进行预测，为充电设施的规划提供了参考。文献[5]通过研究价格型需求响应引导用户响应电价的变化以调整用电需求，对于用电需求的计算主要基于用户在行程结束后的慢速充电。

现有的电动汽车充电研究主要针对于电动汽车在工作日到家后的充电策略，且大部分研究的充电模式为慢速充电，相对较少考虑到电动汽车长途出行的情况[6-8]。为了在保障用户出行需求的前提下对用户出行与充电进行引导以达到有效改善电动汽车用户里程焦虑与充电难的目的，笔者建立了电动汽车路径选择模型，在电动汽车长途出行时对其行驶路径搜索方式进行规划，避免电动汽车陷入在行驶过程中能量用尽的困境。并且提出了3种不同的充电引导策略，根据用户的偏好对3种策略下的算例进行仿真，比较得出用户的偏好对充电站负荷的影响。最后通过对比引导前后用户满意度的变化，证明所提出的引导方法的有效性。

1 电动汽车充电时间与等待时间模型

将电动汽车出行路径上的起点、终点、充电站转化为节点进行分析。长途出行过程中，电动汽车用户将从起始节点出发，中途经过路口节点，并在充电站节点充电后继续行驶，最后抵达终点节点，电动汽车长途出行路径如图1所示。

图1 电动汽车长途出行路径示意图

与燃油车不同，电动汽车在路径规划中需要重视电量的消耗问题，因此在寻找最优路径时，需要首先考虑电动汽车能否在电量耗尽前到达下一个充电站[9]。因此，电动汽车可以首先以充电站为目标进行路径规划，到达充电站后，以寻找下一个充电站为目标进行后续路径规划，直到电动汽车电量足以到达终点，最后以终点为目标进行路径规划。电动汽车到达充电站节点后，根据剩余电量是否可以支持从当前节点到下一节点的路程所需，电动汽车将判断是否需要进行充电。

(1)

(2)

式中：pathstart-end为起点到达终点的路径；pathstart-1为从起点到第一个充电站的路径；pathi-(i+1)为从第i个充电站到达第i+1个充电站的路径；pathn-end为从第n个充电站到达终点的路径；tstart-end为从起点到终点耗费的时间；tpath为行进路径上耗费的时间；tchar为充电耗费的时间；twait表示等待充电耗费的时间。

2 考虑长途出行用户偏好的电动汽车充电引导策略

为尽量满足长途出行用户的出行需求[10-11]，从电动汽车用户的利益出发，分别采取充电次数最少、路程最短、时间最短3种充电策略，引导电动汽车经过合适的路径到达终点。

2.1 充电次数最少策略

受充电费用、充电流程等的影响，用户满意度往往与充电次数成正比，故采用充电次数最少策略。若想要达到充电次数最少的效果，在行驶途中，应尽可能充分利用所充电量，即应尽可能选择在可行路径中较远的充电站作为下一行驶目标。充电次数表示如下：

(3)

式中：n为区域内充电站数量;δi为第i个充电站的充电系数，其值为1表示电动汽车在该充电站充电，其值为0表示电动汽车在该充电站不充电。

基于本文对于长途出行的定义，电动汽车在出行中至少会充一次电，故充电次数限制为：

1≤f1≤n

(4)

2.2 路程最短策略

为减少开车时间、减少电动汽车能量损耗，不少车主会倾向于选择路程最短的出行方式，该策略也是传统出行的规划方法，但在电动汽车的出行过程中可能其效果弱于传统燃油车。在本策略中，为实现路程最短，需要在可行路径中对起点到终点的路径进行规划，选出其中最短的路径。路程表示如下：

(5)

式中：N为电动汽车出行路径上经过的节点数；li→i+1为从路径上的第i个节点到第i+1个节点的路程。

2.3 时间最短策略

为了减少出行时间，需综合考虑路程消耗时间和充电站消耗时间，计算公式如下：

f3=t1+t2+t3

(6)

(7)

(8)

(9)

式中：t1为路程消耗时间；t2为电动汽车充电消耗时间；t3为电动汽车等待充电消耗的时间；v为电动汽车出行速度；ti,char为电动汽车在第i个充电站充电需要的时间；ti,wait为电动汽车在第i个充电站等待充电需要的时间。

为了对区域负荷进行改善，当区域负荷过大时应对电动汽车充电站进行限制，本文假设充电等待时间与负荷的关系如式(10)所示。

(10)

3 基于改进型dijkstra算法的电动汽车路径搜索方法

原始dijkstra算法[12]中，从当前节点出发，基于贪心原则，即在求解的每个步骤中都寻求最优解，依次计算当前节点到下一个节点直到目标节点的路径距离，最终求得最短距离。在本文中，由于电动汽车能量的限制，所求路径必须满足电动汽车能量限制才能成为可通行路径。在路径搜索的过程中，由于电动汽车需要多次充电，故可将电动汽车行驶路径划分为多个由前一个充电站到达后一个充电站的路径。基于dijkstra算法的特点，用户从起点出发，依次计算到达每个节点的最短距离，故用户在每个位置都是从起点到达该位置的最短距离。根据这一特性，可以将时间加入最短路径的计算过程中，即在到达充电站后计算路程消耗时间，计算此时充电需要等待的时间以及充电需要花费的时间，以上三者相加即为从该点出发到达终点所需要的时间。路径规划流程如图2所示。

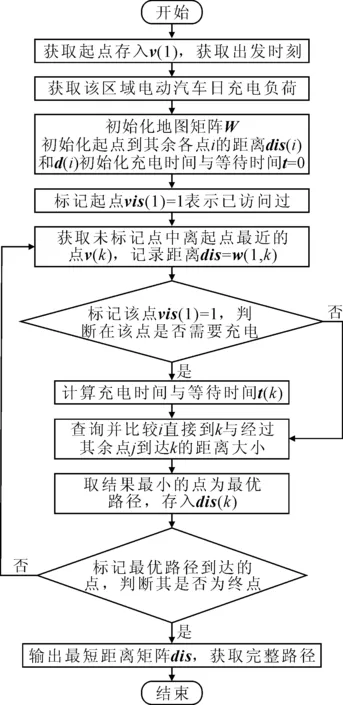
图2 路径规划算法流程图

具体计算步骤如下：

步骤1获取起点与出发时刻，获取区域电动汽车充电负荷信息，获取地区地图信息，并将路程转化为所需时间，得到距离矩阵W，表示直接联通的两点之间的距离所需行驶的时间；

步骤2起点设为v(1)，初始化dis(i)，d(i)的值为v(1)到其余点v(i)的距离w(1,i)，如果两节点可以直接连通，则距离初始化为两点间的路程消耗时间，否则初始化为无限大，初始化每个节点的充电与等待时间之和t(i)为0；

步骤3将v(1)标记，vis(1)=1(vis(:)一开始初始化为0)，表示该节点已被访问过；

步骤4找寻与v(1)相邻的最近点v(k)，将v(k)点记录下来，v(k)与V(0)的距离记为min；

步骤5把v(k)标记，vis(k)=1；

步骤6计算v(k)节点的充电时间与等待时间t(k)；

步骤7查询并比较，让dis(j)与min+w(k,j)+t(k)进行比较，判断否存在另一个点v(j)使得经过该点时两节点间距离最小，即dis(j)=MIN(dis(j),min+w(k,j)+t)；

步骤8继续重复步骤3到步骤5，直到找出所有点为止。

步骤9输出路径节点信息，计算到达每个节点的时间与充电信息。

4 仿真算例分析

4.1 仿真场景设置

选取某地区的路网进行仿真分析，路网如图3所示。图3中共有24个节点，除节点1和节点20外都为充电站节点。为便于计算，在运算开始前将路网中每段路径长度设为固定值，具体为随机取50～150 km之间的值得到。本次仿真中，电动汽车从节点1出发到达节点20，路途中若需要充电则采取前文所述3种策略进行充电路径规划。

图3 路网图

基础家庭用电负荷为随机选取的美国中西部200个家庭的一天内用电负荷，以10 min为间隔进行统计，该数据为包含了家庭生活用电及电动汽车无序充电的总负荷。一天内基础负荷的变化趋势如图4所示，从图4可知，17～21点之间家庭用电负荷达到峰值，在8～12点之间家庭用电负荷达到次峰值，晚上0～5点及中午13～15点之间负荷较小。

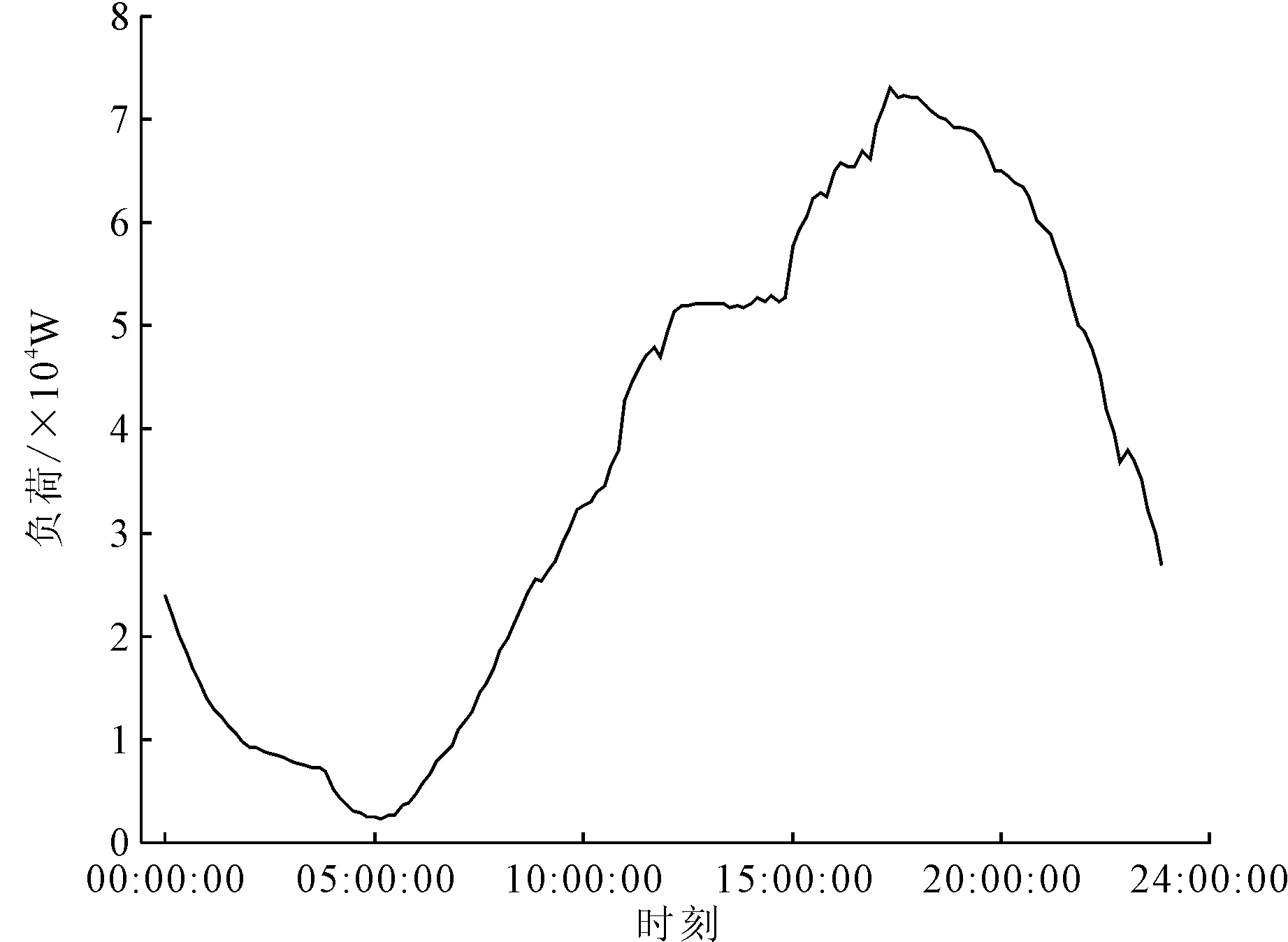
图4 区域内日负荷趋势

仿真选取的电动汽车最大行驶里程设为300 km，假设电动汽车充电方式都为直流快速充电，每小时充电量可供行驶里程为240 km。根据道路限速要求，假设电动汽车行驶速度恒定为60 km/h，耗电量与行驶里程成线性正相关。

4.2 电动汽车出行起始时刻对充电路径的影响

由于长途出行跨越时间较长，电动汽车很有可能会在电网负荷较高时需要进行充电。为了避免与用电高峰相遇，笔者对不同出发时间的电动汽车路径进行研究，探索出发时间与出行路程、出行时间以及充电次数的关系，并对仿真结果进行分析。考虑到长途出行时间较长，同时为了避免夜间疲劳驾驶，通常情况下，用户将行程安排在白天，故选取9点、10点、11点3个时刻出发的出行状况对电动汽车长途出行进行分析。表1～表3分别为9点、10点、11点出发的电动汽车路程最短的10条路径。

表1 9点出发的电动汽车路径

从表1～表3可知，随着出发时间的延后，总时间和路程也呈增加的趋势，充电次数由于路程的增加也有略微地增多，但因为总路程变化范围较小，充电次数的变化不太明显。在相同出发时间下，总时间与路程没有绝对的正比关系，这是因为不同路径充电时需要的等待时间不一样，因此，在选择充电路径时不能以最短路程为选择目标，应综合考虑用户的偏好与需求来确定路径。

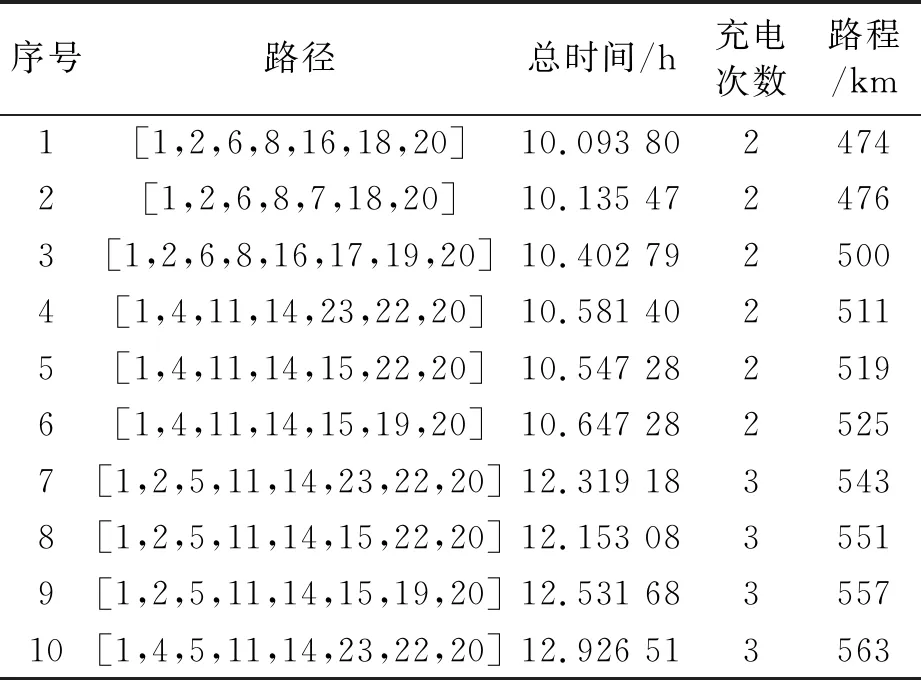
表2 10点出发的电动汽车路径

表3 11点出发的电动汽车路径

4.3 用户满意度

路径规划的结果直接作用于相应的用户，因此可以根据用户的满意度对其效果进行评价，笔者根据用户需求的出行时间、出行路程、充电次数对用户满意度进行量化，满意度量化公式为：

(11)

式中:nmin、nmax分别为最少、最多充电次数；smin、smax分别为最短、最长总路程；tmin、tmax分别为最短、最长总时间。

由于最多充电次数、最长路程与最长时间都为无限大，因此结合本例的特点，在此分别对三者进行排序，取第二十位为最大值，即取得nmax=4，smax=663 km，tmax=14.5 h。

分别计算得到3种策略下的充电次数、路程、时间、满意度，结果如表4所示。

表4 用户满意度

从表4可知，充电次数与总时间关联度较高，进而影响用户满意度。在本例中，充电次数变化范围太小，因此上述满意度计算方法对充电次数的敏感性将会过高，需要对其进行改进。基于充电次数与总时间的相关性，将满意度计算公式中的充电次数去掉，将另外两个影响因素进行归一化后取相同权重，改进后满意度计算公式如下：

(12)

改进后的用户满意度如表5所示。

表5 改进后的用户满意度

从表5可知，在充电次数和总时间变化时，路程变化不大，这是因为充电次数与总时间较小时，在路程上花费的时间相应也较少。充电次数与总时间关联性较大，因此在充电站排队时间较短时，充电次数将直接影响总时间。对满意度的影响从大到小依次为充电次数、充电时间、总路程。与传统的以路程最短为导向的路径规划相比，以充电次数为导向的路径规划方法用户满意度更高。

5 结论

电动汽车长途出行具有总时间长、总路程长、需要多次充电等特点。电动汽车在出行过程中，当所剩电量不足以支持到下一个充电站时，电动汽车需要进行充电，充电时间与充电功率与及电量需求有关。

由于大部分电动汽车充电时间较为集中，故本文通过区域内电动汽车充电负荷近似代表充电车辆数，从而计算排队时间。而排队时间的差异造成了出发时间对于电动汽车出行的影响。因此在规划电动汽车出行时，出行时刻对出行情况也有较大的影响，需要根据路程长度及充电高峰时间进行调整。

根据分析3种不同的需求充电策略，可以看出充电次数对于用户满意度影响较大，同时充电次数也影响着出行总时间，因此把握好电动汽车出行时的充电次数对于用户出行十分关键。对比只考虑路程最短的传统路径规划方法，考虑充电次数的路径规划方法对于电动汽车出行具有更好的效果。