制动工况下危险品液罐车内液体晃动冲击及其影响因素研究

肖陈陈，李刚炎，杨 凡，赵 燃

(武汉理工大学 机电工程学院，湖北 武汉 430070)

危险品液罐运输车是一种运输液态危险货物的专用车辆，其在运行时不仅要承受内压或外压载荷，还会受到罐内液体晃动引起的冲击力和惯性力的作用。由于罐车运输的危险品液体大多具有易燃、易爆或腐蚀的特性，一旦发生交通事故导致泄漏，后果十分严重[1]。液体晃动是指带有自由液面的液体在有限空间内发生的运动，其特点是存在自由界面[2]，这是一种复杂的流体运动现象。目前，通过分析液体晃动特性和改善罐体结构等方法提高液罐车行驶稳定性的研究已有很多[3-6]，但针对影响因素的分析很多没有考虑防波板的影响，针对罐内液体冲击对液罐车实际制动减速度的影响的研究也相对较少。

笔者通过分析危险品液罐车制动时罐内液体的运动情况，构建了制动工况下危险品液罐车罐内液体晃动理论模型。应用商用CFD(computational fluid dynamics)软件Fluent构建了制动工况下危险品液罐车罐内液体晃动仿真环境并进行了仿真分析。研究了初速度、初始制动减速度和充液比3种影响因素对制动工况下危险品半挂运输车罐内液体纵向冲击力以及车辆有效制动减速度的影响，并得到了3种因素对所选取试验指标的影响程度排序。

1 液体晃动理论模型

危险品液罐车在行驶时液体与罐体以相同速度前进，两者的相对速度为零。当车辆开始制动时，罐体即以一定减速度开始减速，而罐内液体由于惯性，仍向车辆行驶方向运动，并对罐体产生动压力[7]，其内部为气液两相非定常湍流流动。笔者采用VOF(volume of fluid)模型处理气液相互作用产生的两相流现象[8]，其理论公式如下：

连续方程：

(1)

动量方程：

(2)

式中：u为速度；p为压强；ρ和μ在VOF模型中分别为体积分数的平均密度和分子运动粘度。

ρ=αfρf+(1-αf)ρa

(3)

μ=αfμf+(1-αf)μa

(4)

式中：αf为液体的体积分数；ρf和ρa为液体和气体的密度；μf和μa分别为液体和气体的动力粘性系数。

2 液体晃动仿真环境构建与试验组设计

2.1 液体晃动仿真环境构建

Fluent软件作为CFD软件的领先者，其中包含了丰富的模块。笔者采用Fluent中的多相流VOF模型对危险品液罐车在制动工况下的罐内液体晃动进行分析。

以某典型危险品液罐车为研究对象，其罐体几何尺寸及防波板尺寸如图1所示。罐体内径r=1 235 mm，罐体壁厚为14 mm，两端为平封头，厚度为16 mm，罐体总长9 240 mm，容积为44.188 m3。防波板的厚度为5 mm，并将其从左向右依次定义为B1、B2、B3、B4、B5、B6。防波板样式为弓形板，弓形板底部与水平轴线距离为197 mm。

图1 罐体几何尺寸及防波板尺寸

采用Solidworks软件建立装有弓形防波板的液罐模型。以罐体的运动方向为X轴正向，垂直地面向上为Z轴正向，建立空间直角坐标系。为便于后续流体分析，仅建立液罐的流体域模型，然后导入Fluent中完成流体域网格划分。完成有关设置后，用Fluent中的VOF模块研究制动力作用下液罐内液体的晃动。

危险品液罐车制动工况下罐内液体晃动的模型可以分为两种：①开始时刻液体与罐体以共同速度前进，即相对速度为零，罐体壁面不受任何的动压力。从t=0时刻开始，罐体以加速度a开始减速，液体由于惯性，部分会穿过防波板向罐体前侧涌动，撞击前封头后又向后侧运动，产生纵向的动压力；②开始时刻液体和罐体都保持静止，从t=0时刻起给液体施加加速度a，让液体加速运动，罐内液体开始晃动。

以上两种模型，前者更接近实际工况，但其建模过程比较复杂。后者的建模过程更方便，可以减少大量计算时间。卜凯[9]对这两种模型进行了仿真对比，结果基本一致，故采用第二种模型进行仿真。

2.2 液体晃动的单因素试验设计

为研究危险品液罐车在制动时罐内液体冲击与影响因素间的关系以及这些因素对制动的影响，选取了制动初速度等3种因素进行仿真。以罐内液体对前封头的最大冲击力以及有效制动减速度作为试验指标[10]。有效制动减速度aυ的计算公式如下：

maυ=mgφ-F

(5)

式中：m为危险品液罐车总质量；F为液体纵向冲击力；φ为地面附着系数，一般取为0.7；g为重力加速度。

根据标准，汽车罐车的行驶速度不超过 80 km/h，车辆制动器的制动减速度为 5.8～7.65 m/s2。同时，液罐车的罐内充液比应控制在0.5～0.9之间。为了得到相应的结果，利用控制变量法，划分不同试验组，如表1所示。

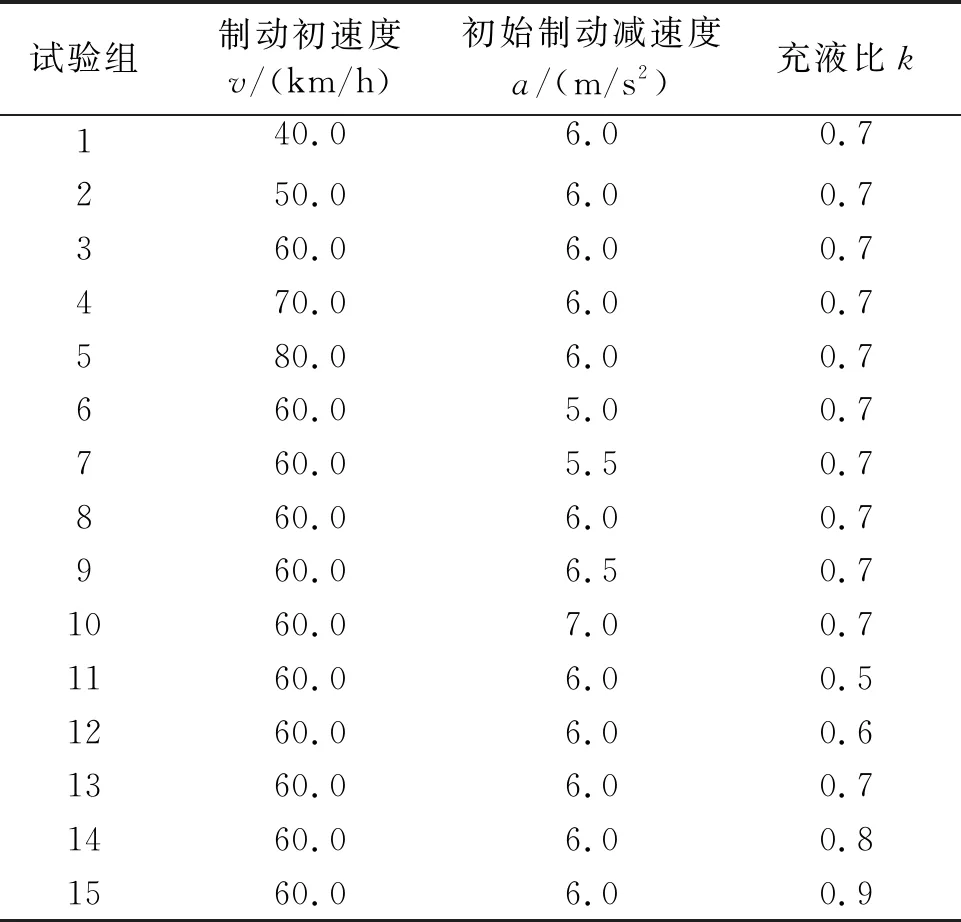
表1 单因素试验组

2.3 液体晃动的均匀试验设计

为了分析3种影响因素对试验指标的影响程度大小，采用均匀设计试验，试验因素为：制动初速度A，初始制动减速度B，充液比C。以此划分不同试验组，均匀试验因素水平和均匀设计试验方案如表2和表3所示。

表2 均匀试验因素水平

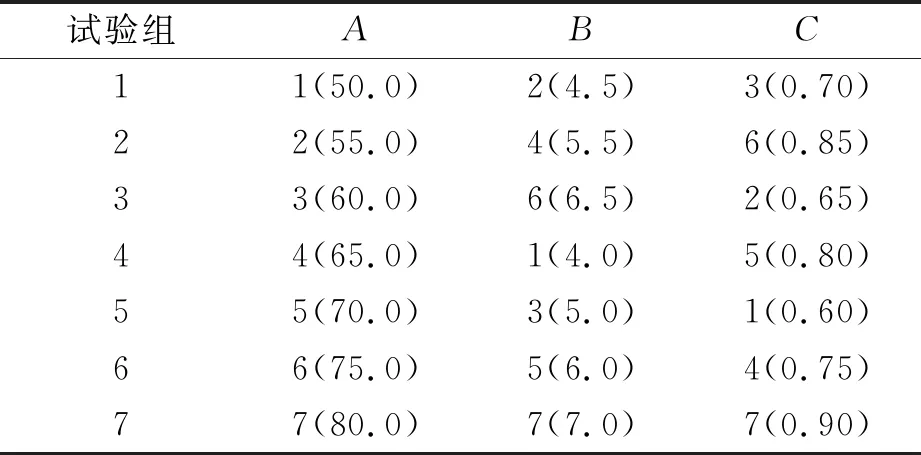
表3 均匀设计试验方案

3 液体晃动的影响因素分析

3.1 不同因素对罐内液体纵向冲击力的影响

根据表1的分组，分别讨论制动初速度等3种因素对罐内液体纵向冲击力的影响。其中1～5试验组制动减速度和充液比不变，制动初速度从40 km/h变化到80 km/h。6至10试验组充液比和制动初速度不变，初始制动减速度从5 m/s2变化到7 m/s2。11至15试验组制动初速度和初始制动减速度不变，充液比从0.5变化至0.9。仿真结果如图2～图4所示。图中kz1意为第一个试验组的结果，以此类推。

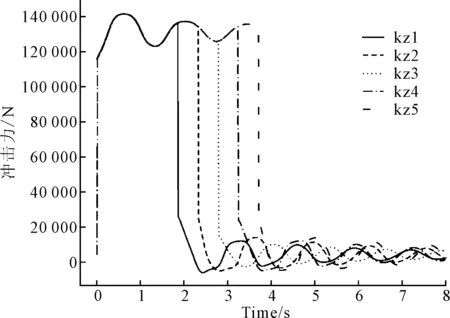
图2 不同制动初速度下的纵向冲击力曲线

图3 不同初始制动减速度下的纵向冲击力曲线

图4 不同充液比下的纵向冲击力曲线

从图2可知，开始制动后，液罐车罐体前封头受到的纵向冲击力由零快速上升，大约在0.60 s左右上升到最大值。因为在开始制动后，罐内部分液体在惯性力的作用下穿过防波板向罐体前壁运动并撞击前壁，使得罐体受到了增大的纵向冲击力。当纵向冲击力达到最大值之后，其在一定时间内逐渐减小，减小到一定程度后，保持在一定范围。当车辆制动结束后，液罐车罐体前封头受到的液体冲击力迅速降低，并且保持在一定范围内。

为了便于分析不同因素对罐内液体纵向冲击力的影响，主要关注纵向冲击力峰值大小、纵向冲击力上升到最大值的时间、纵向冲击力波动情况及持续时间。根据图2～图4可得不同因素对罐内液体纵向冲击力的影响，结果如表4所示。

表4 不同因素对罐内液体纵向冲击力的影响

3.2 不同因素对液罐车有效制动减速度的影响

在利用Fluent软件求解出作用在罐车上的纵向冲击力的大小后，由有效制动减速度的计算公式可得出不同因素下液罐车有效制动减速度的变化曲线，如图5～图7所示。

图5 不同初速度下的有效制动减速度曲线

图6 不同初始制动减速度下有效制动减速度曲线

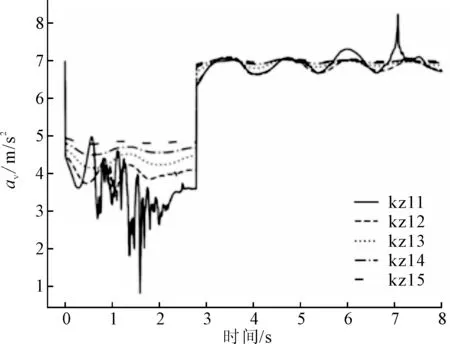
图7 不同充液比下的有效制动减速度曲线

从图5可知，开始制动后，液罐车的有效制动减速度迅速降低，并大约在0.60 s左右下降到最小值。这表明液罐车开始制动时，即使有防波板的防波效果，但罐内液体晃动对液罐车罐体产生的冲击力仍使车辆实际的减速度远远低于6 m/s2。说明在制动开始后的初期，液体的晃动会影响液罐车的制动性能，使得液罐车的有效制动减速度大大降低。

同理，为了便于分析不同因素对液罐车制动时有效制动减速度的影响，主要关注有效制动减速度的最小值、下降到最小值的时间、波动情况及持续时间。根据图5～图7可得不同因素对液罐车有效制动减速度的影响，如表5所示。

3.3 不同因素对试验指标的影响程度

通过仿真得到不同组罐内液体纵向冲击力和车辆有效制动减速度曲线，如图8和图9所示。

使用Minitab软件对3个因素(制动初速度A，初始制动减速度B，充液比C)下最大纵向冲击力出现时间Y1、纵向冲击力的最大值Y2、有效制动减速度的最小值Y3的影响程度进行分析。

表5 不同因素对液罐车有效制动减速度的影响

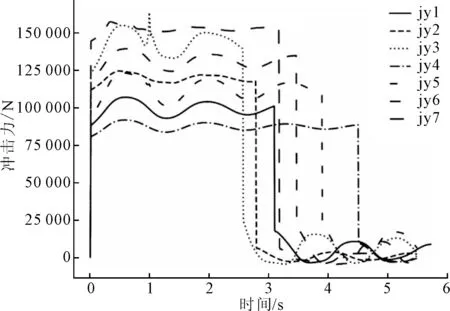
图8 均匀试验中各组罐内液体纵向冲击力曲线

图9 均匀试验中各组罐内液体制动减速度曲线

对试验结果进行拟合，得到表达式为：

(6)

根据仿真结果可知，对于Y1，3个因素影响程度为C>B>A，且3个因素均与Y1呈负相关。对于Y2，3个因素影响程度为B>C>A，且A、B与Y2呈正相关，C与Y2呈负相关。对于Y3，3个因素影响程度为B>C>A，且A、C与Y3呈正相关，B与Y3呈负相关。

4 结论

针对危险品液罐车，选择带防波板的罐体，用Fluent软件构建了制动工况下液罐车罐内液体晃动仿真环境。采用单因素试验，分别对初速度、初始制动减速度和充液比3种因素进行了仿真分析，得到了不同因素对制动工况下危险品液罐车罐内液体纵向冲击力及有效制动减速度的影响。采用均匀试验设计得到了3种因素对试验指标的影响程度大小。根据拟合结果可知，充液比更能影响最大纵向冲击力的出现时间，而初始制动减速度则更能影响纵向冲击力的峰值以及有效制动减速度的最小值。为之后不同防波板的性能仿真测试奠定了基础。