基于Flowmaster与Simulink的发动机冷却系统变论域模糊控制

程 鑫,夏一恒,刘一鹏,彭 程

(1.武汉理工大学 机电工程学院，湖北 武汉 430070；2.湖北省磁悬浮工程技术研究中心，湖北 武汉 430070)

汽车冷却系统需满足车辆在各种工况下的发动机及附件的散热需求，其设计的优劣程度直接影响车辆的发动机性能。因此保证发动机在最佳温度范围内工作，是发动机冷却系统设计的主要目标[1]。

在传统的冷却系统中，水泵和风扇由发动机曲轴带动皮带轮以机械方式驱动[2]，因此发动机冷却系统的散热量控制不精准，容易出现“过热”或者“过冷”现象[3]。汽车电子水泵实现了冷却水泵的独立驱动，它不受发动机转速影响，可根据实际冷却需求灵活工作，现广泛应用于电动汽车的冷却系统中[4]。

现阶段对于冷却系统性能的优化设计主要有两种途径，其一为优化冷却系统的各元器件性能，如李金徽[5]通过提高冷却系统的进风系数、冷却液循环中的除气能力，在现有车型的基础上增加挡风板和优化除气管路，提高了冷却系统的冷却能力；唐海国等[6]应用田口方法对冷却系统进行了稳健性设计，结合仿真分析，以较少的实验组合得到各可控因子影响特性，结合工程成本和周期因素，得到元器件的最佳改制方案；其二为优化冷却系统中元器件的控制策略，如乔方方[7]基于Flowmaster进行发动机冷却系统的一维-三维联合仿真，改善冷却系统各换热器的相对位置，提高换热效率和发动机的舱内热环境；杨鸿镔等[8]对电子水泵使用了脉谱前馈与模糊控制法，对重型柴油机的瞬态冷却系统进行仿真研究，做到了根据车辆运行状态实时控制冷却系统散热量；吕良等[9]在建立冷却系统传热动力学模型的基础上，基于Lyapunov Stability设计了冷却系统的非线性控制器和扰动观测器，显著提高了冷却系统的控制精度。

综上所述，考虑到汽车运行的实际工况多变，以及传统控制的局限性，以提高冷却液温度控制精度和稳定性为目标，最终确定对电子水泵的控制策略为变论域模糊控制，并通过Flowmaster和Simulink联合仿真，在全球轻型车统一测试循环( world light vehicle test cycle,WLTC)工况下对优化后的控制策略进行验证。

1 基于Flowmaster的冷却系统建模

汽车发动机冷却系统一般包括发动机套管、水泵、节温器、散热器、风扇、膨胀水箱、热风元件以及由连接这些元件的硬管和软管组成的循环管路等。在水泵的驱动下，冷却液在循环管路内流动，流经散热器冷却降温后，重新流入发动机水套，形成冷却循环。发动机冷却系统一维稳态模型如图1所示。

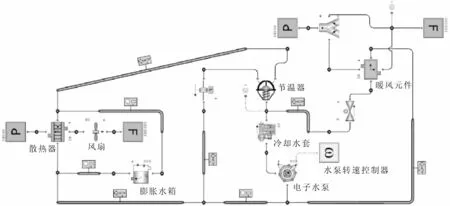
图1 发动机冷却系统一维稳态模型

1.1 发动机水套模型

发动机水套是冷却液在发动机内循环流动的管道，它能将发动机燃烧室和缸体内壁的温度通过热传导将热能转移到冷却液。

2021年7月1日起，传统能源乘用车、插电式混合动力电动乘用车试验工况将由新欧洲驾驶循环周期(new European driving, NEDC)工况切换为WLTC工况。为更真实地模拟发动机瞬态工况下的产热，采用WLTC工况为试验工况，它模拟了一条更动态的路径，更广泛的驾驶条件，且可单独增加可选配置，更符合实际驾驶工况，该工况下发动机的转速、扭矩与时间的关系如图2所示。

图2 WLTC工况下的发动机转速与扭矩图

发动机的产热由发动机的转速和扭矩决定，冷却液与发动机水套之间的传热系数采用默认值。发动机基本参数如表1所示。

表1 发动机基本参数

发动机热功率与发动机转速和扭矩的关系式如下：

P=K·T·v

(1)

P热=η·P

(2)

式中：P为发动机总功率；K对于同一辆车而言是一个常数；T为发动机扭矩；v为发动机转速；P热为发动机的热功率；η为发动机的热效率，文中取30%。

假设发动机怠速及输出扭矩为零时，发动机功率不小于10 kW，即发动机散热需求不小于3 kW。根据式(1)和式(2)，可得在WLTC工况下该发动机的产热随时间变化的曲线如图3所示。

图3 发动机在WLTC工况下的产热曲线

1.2 电子水泵模型

冷却液流经系统各部件时会产生压力损失，尤其在发动机水套内。水泵作为冷却系统中的唯一动力源，能够给冷却液加压，保证其在冷却系统中循环流动，是实现控制冷却系统冷却量的关键。

电子汽车水泵相较于传统水泵，采用直流电机作动力装置，不同工况下可实现精确调控电机转速，从而实现冷却液传输的可调性和精确性。

在Flowmaster建模过程中，需要对水泵特性参数进行Suter无量纲化，转换公式如下：

Q*=Q/QR

(3)

H*=H/HR

(4)

ω*=ω/ωR

(5)

T*=T/TR

(6)

(7)

(8)

(9)

式中:Q为水泵流量；QR为水泵的额定流量；Q*为水泵流量的无量纲参数；H为水泵扬程；HR为水泵的额定扬程；H*为水泵扬程的无量纲参数；ω为水泵转速；ωR为水泵额定转速；ω*为水泵转速的无量纲参数；T为水泵扭矩；TR为水泵额定扭矩；T*为水泵扭矩的无量纲参数；WH和WT分别为Suter形式的H和T；θ决定了水泵的运行特征。

通过数据拟合的方式得到了水泵流量与扬程曲线及其Suter形式曲线，如图4和图5所示。

图4 水泵流量-扬程曲线

图5 水泵流量-扬程Suter曲线

1.3 节温器模型

节温器能根据冷却液温度的高低自动调节进入散热器的冷却液量，改变冷却液的循环面积，调节冷却系统的散热能力。节温器的开度与冷却液温度的关系如图6所示。

图6 节温器开度-冷却液温度关系曲线图

当冷却液温度低于节温器开启温度时，节温器内的石蜡呈固态，节温器的阀体闭合，冷却液不流经散热器，只进行小循环，从而使发动机温度快速上升。到达规定温度后，石蜡开始融化为液态，体积膨胀，顶起阀门，受热冷却液流经散热器进行散热处理后，重新流入发动机水套，吸收发动机产生的热量，形成大循环通路。

1.4 散热器模型

散热器主要由进水室、出水室及散热器芯3部分构成。散热器是一个热交换器，冷却液在散热器芯内流动，空气在散热器芯外通过。热的冷却液由于向空气散热而变冷，冷空气则因为吸收冷却液散出的热量而升温，为了将散热器传出的热量尽快带走，一般在散热器后面装有风扇与散热器配合工作。

换热元件及发动机水套的压损和流量关系，一般情况下满足式(10)。

ΔP=aQ2+bQ

(10)

式中:ΔP为管路压损情况；Q为冷却液体积流量；a、b为拟合系数。

笔者采用数据拟合的方式得到冷却液侧流阻和空气侧流阻曲线如图7和图8所示。

图7 冷却液侧流阻曲线

图8 空气侧流阻曲线

2 冷却系统变论域模糊控制

2.1 变论域模糊控制原理

变论域是相对于常规模糊控制的固定论域而言。对于模糊控制，如果固定论域的初始范围设计过小，容易造成输入量和输出量超出论域，控制器失去应有的控制；如果论域范围设计过大，则会造成控制精度降低，控制结果稳定性下降。

变论域模糊控制是在模糊控制的基础上，根据输入误差和误差变化率的大小，得出相应的伸缩因子，在论域与相应的伸缩因子相乘之后，论域就会相应变化，其对应的隶属度函数也会变化，这就相当于间接精细化了控制规则，控制会变得更加敏感，从而提高了控制精度。

一般模糊控制器输入的初始论域为[-E,E]，输出的初始论域为[-Y,Y]。经过与伸缩因子α(t)和β(t)相乘之后的论域分别为[-α(t)E,α(t)E]、[-β(t)Y,β(t)Y][10]。论域的伸缩变化如图9所示。

图9 论域变化图

对于伸缩因子的选择，可以通过模糊推理或者函数两种方式来确定。其中，伸缩因子有如下几种函数形式：

(11)

α(x)=1-λ-kx2

(12)

(13)

式中：α(x)为输入论域的伸缩因子；τ>0；ε为足够小的正数；λ∈(0,1)；k>0；β(x,y)为输出论域的伸缩因子。

2.2 变论域模糊控制结构

要实现变论域模糊控制，需将输入论域、输出论域、隶属度函数都乘以相应的伸缩因子，计算繁琐，导致控制系统的响应速率变慢，特别是当论域为实数域时，逐点变换难以实现。因此，通常采用一种等价变换的方式[11]，即将量化因子除以输入论域的伸缩因子，将比例因子乘以输出论域的伸缩因子。变论域模糊控制器结构如图10所示。

图10 变论域模糊控制器结构图

该控制器主要包括3个模块：

(1)伸缩因子推理模块。计算反馈得到的温度误差e和误差变化率ec，通过设定好的伸缩因子模糊推理规则，得出输入变化量e和ec的伸缩因子αe，αec，以及输出变量ΔNf的伸缩因子βNf，然后将量化因子Ke和Kec分别乘以输入论域伸缩因子ae，aec,将比例因子KNf乘以伸缩因子βNf。对整个控制器的论域进行伸缩处理；

(2)模糊控制器模块。将输入变量模糊化后按模糊控制器内制定好的规则进行模糊推理，获得模糊化的参数调整值ΔNf；

(3)模糊值清晰化模块。常用的精确化方法有最大隶属度法和重心法。在本次仿真中选用重心法，将推理得到的模糊子集的隶属度函数与横坐标所谓面积的重心所对应的标准论域元素作为精确化结果，按对应关系得到最终控制量Nf。

变论域模糊控制器参数如表2所示。

表2 变论域模糊控制器参数

2.3 模糊规则制定

模糊规则与传统条件规则的不同之处在于，传统条件推导出的结果要么是，要么不是；模糊规则推导出的的结果则为一定程度上是，一定程度上不是。为了得到最后的推理结果，需要判定结果的隶属程度。

系统的控制规则库是由若干条规则组成，对于每一条推理规则都可以得到一个相应的模糊关系。模糊规则控制表如表3所示，ΔNf的模糊规则MAP图如图11所示。

表3 变论域模糊控制规则表

图11 ΔNf的模糊规则MAP图

3 Flowmaster与Simulink的联合仿真

3.1 联合仿真模型

使用Flowmaster Interface接口模块传递转速和温度信号，实现Flowmaster和Simulink的联合仿真，联合仿真图如图12所示。

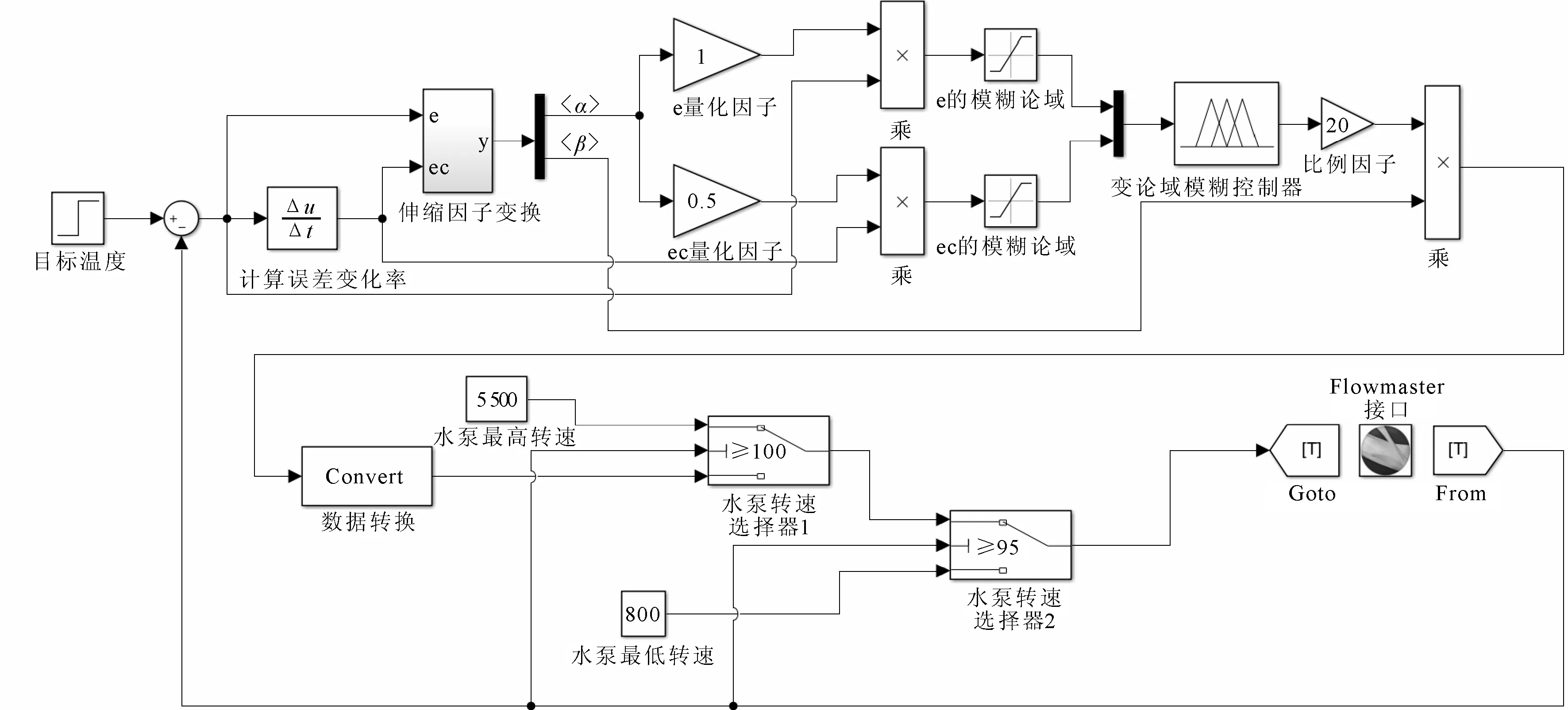
图12 变论域模糊控制的Simulink联合仿真图

3.2 联合仿真结果及分析

为模拟汽车从启动到各工况冷却系统对目标温度的跟随性，同时考虑到电控式发动机正常工作时冷却液温度95～105 ℃，设定环境温度和冷却液初始温度为30 ℃，目标冷却液温度为95 ℃，仿真步长0.5 s。

采用模糊控制和变论域模糊控制的温度控制效果对比结果如图13和图14所示。

图13 变论域模糊控制和模糊控制全过程效果对比图

图14 变论域模糊控制和模糊控制作用后效果对比图

从图13和图14可知，从发动机起步暖机到节温器开启阶段，电子水泵不工作，变论域模糊控制和模糊控制的效果一致；节温器开启之后，变论域模糊控制能够更灵敏地响应当前温度与目标温度之间的偏差，一方面能使出口冷却液温度更快地到达目标温度；另一方面目标温度附近的波动量也更小。表4对比了两种控制方法作用后的冷却系统关键性能参数。

表4 两种控制方法作用后的冷却系统性能对比

在模糊控制和变论域模糊控制下，冷却液温度从常温(30 ℃)升到目标温度(95 ℃)的时间分别为458 s和405 s，后者所用时间减少了53 s，温度控制的快速性提升了11.57%；冷却液温度升到目标温度之后，模糊控制和变论域模糊控制将冷却液温度控制在目标温度的±0.5℃之内的时间分别为1 119 s和1 330 s，所占时间的比例分别为83.38%和95.34%，温度偏差绝对值0.5 ℃以内的时间比例增加了11.96%；当控制方法从模糊控制优化成变论域模糊控制后，冷却液温度偏差范围从[-1.696,1.672]变为[-0.815,1.173]，温度的最大波动区间减小了40.97%。

因两组数据的平均数不同，故不能采用标准差，而需采用标准差系数cv来量化衡量两种控制效果的稳定性。标准差系数的计算公式为：

(14)

(15)

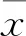
由式(14)和式(15)可得，cv_fuzzy=0.09，cv_variable=0.06，故cv_fuzzy

4 结论

相较于模糊控制策略，对电子水泵的转速进行变论域模糊控制能更快地让发动机出口冷却液温度到达目标温度，快速性提升了11.57%；还能够更精确、更稳定地控制冷却液温度在目标温度95 ℃附近，冷却液温度波动幅度减小了40.97%，温度偏差±0.5 ℃的时间增加了11.96%。因此，变论域模糊控制是一种高效可行的电子水泵控制策略。仿真模拟的工况没有考虑车辆运行过程中的环境风量、地面平整度、温度变化等因素，而这些因素都会影响控制策略的效果；没有考虑高频控制对水泵寿命、系统能耗的影响；没有进行实际运行试验，缺乏对仿真结果的进一步验证，在后续研究中有待进一步完善。