复杂系统结构建模分析
王鹏程,黄 祺,肖人彬
(1.华中科技大学 人工智能与自动化学院,湖北 武汉 430074;2.云骧网络科技(上海)有限公司,上海 200439)
结构模型(structural model)描述的是系统的结构性态,它是从系统的概念模型过渡到定量分析的中介[1];而建立结构模型的过程就是结构建模(structural modeling)。现有结构建模方法较多,如:解释结构建模(Interpretive Structural Modeling,ISM)[1]、决策实验室分析法(Decision Making Trial and Evaluation Laboratory,DEMATEL)[2]、系统动力学(System Dynamics,SD)[3]、交叉影响分析(Cross Impact Analysis,CIA)[4]等。其中,系统动力学由Forrester于20世纪50年代始创于美国[5],它以定性分析为先导,以定量分析为支持,特别适宜分析解决社会、经济、生态等复杂系统问题,有“政策实验室”之称[6],在国际上影响很大;而由Warfield[7-10]提出并发展的解释结构建模(ISM)方法适合处理的问题领域众多,覆盖面广,便于操作,应用广泛[11-12]。本文讨论的结构建模就是指ISM,它包括级别划分、区域划分、强连接子集划分等几个主要环节[1,13]。
复杂系统的基本特征是数量巨大、种类繁多、异质性突出、多层次结构[14-15]。现有的ISM方法采用基于递归的逐级迭代方式进行划分操作,是一种拓扑分析方法,对复杂系统进行结构建模时需要分层处理,不仅效率低下,还存在某些隐患(详见第2节论述)。为此本文致力于阐明适于复杂系统结构建模的代数分析途径的优越性,围绕复杂系统结构建模的几个重要问题剖析概念本质,进行原理性分析。
1 结构建模概要
系统的结构模型描述的是系统中各元素之间的关系,如果不考虑关系强弱,则只需要说明是否存在关系。而描述这种元素之间是否存在关系的简便方式就是利用图形。比如图1表示的是数控立车的部分模块之间的关系,从中可看到,立柱对悬臂装置有影响;立柱对横梁升降箱有影响,横梁升降箱又对横梁有影响。前者是直接影响,后者是通过另一模块的间接影响,这些都可以从该图中一目了然。
不仅工程系统可以采用这种图形表示,一些带有社会因素的系统也是如此。图2表示的是一个地区发电供电与工厂、人口、环境之间的关系[1]。从该图中可以看出,工厂数对用电量有影响。工厂数对职工数也有影响,职工数影响到人口数,又影响到用电量。前者是直接影响,后者是通过另两个因素的间接影响。

图1 数控立车模块间关系 图2 地区发电与相关因素间关系
像图1和图2这样的图形表达的是人们对客观世界中各种系统的概念认知,称为系统的概念模型(conceptual model),其中表示元素的圆圈称为节点,表示元素间影响(从抽象意义上讲就是关系)的线段称为边,而影响作用的方向用箭头表示,所以概念模型图是一种有向图。虽然人们难以测辨出复杂系统中元素间的关系哪些是直接关系,哪些是间接关系,但对两两元素之间是否存在关系不难给出,因此系统的概念模型比较容易得到,它也是系统结构建模的起点。
除了用有向图表示系统结构外,还可以使用与之对应的同构矩阵来表征系统的结构,其中与概念模型图相对应的同构矩阵称为邻接矩阵(adjacency matrix)。例如对于图1而言,其对应的邻接矩阵是:
工作台 立柱 横梁 横梁升降箱 悬臂装置

这是一个5×5阶的方阵,它的每一行和每一列都对应图1中的一个节点(代表机床的一个模块)。如果某一模块对另一模块有影响作用,例如工作台对立柱有影响,对应的矩阵元素为1;如果没有影响(例如工作台对横梁),则对应的元素为0。所以邻接矩阵是一个布尔矩阵,即其中的元素只能为0或1。
一般情况下,设系统S中有n个元素,记为
S={x1,x2,…,xn},
(1)
则该系统的邻接矩阵A=(aij)n×n是一个布尔矩阵。aij=1表示xi对xj有影响,aij=0表示xi对xj无影响。其几何意义是:如果在系统概念模型图中,有从节点xi到xj的有向边,则aij取值为1,否则为0。
由邻接矩阵通过下式可求得系统的可达矩阵Re
Re=In∪A∪A2…∪An,
(2)
式中,In为n阶单位矩阵,Re=(rij)n×n中的每一个元素rij表明xi能否到达xj。
通过矩阵运算可知:
In∪A∪A2…∪An=(A∪In)n.
(3)
因此,式(2)可化为
Re=(A∪In)n.
(4)
在可达矩阵的基础上,可以进一步建立系统的结构模型,因此获得可达矩阵是结构建模的关键。为了便于后续讨论,有必要对结构建模中的有关概念给予严格的定义。
设X={x1,x2,…,xn},Y={y1,y2,…,yn}均为有限论域,则X×Y上由谓词确定的二元关系R可用一个n×m阶的布尔矩阵表示。下面将相互对应的二元关系和布尔矩阵视为同一,均记为R。特别地,若X=Y,则称R为X上的二元关系,相应的布尔矩阵是一个方阵。设有限论域X={x1,x2,…,xn},所表征的系统为S,因为S是用X来表征的,故从组成上可将系统记为S={x1,x2,…,xn},其中xi(i=1,2,…,n)称为S的元素。若S′⊆S,则S′称为S的子系统。
有限论域X与由谓词确定的X上的二元关系R之总和,称为X所表征系统的结构模型。结构模型建立的起点是概念模型,该模型可用一个有向图表示,与此有向图同构的矩阵称为邻接矩阵。
定义1设R是X上的二元关系,对∀x∈X,若xRx,则称R是自反的;对∀x∈X,若〈x,x〉∉R,则称R是反自反的。
定义2设R是X上的二元关系,对∀x1,x2,x3∈X,若x1Rx2∧x2Rx3⟹x1Rx3,则称R是传递的。
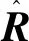
定义4设系统S的邻接矩阵为A,In为n阶单位矩阵,则A∪In的传递闭包称为S的可达矩阵,记为Re。

Re=t(A∪In)=(A∪In)n
(5)
定义5设Re=(rij)n×n为系统S的可达矩阵,若rij=1,则称xi可达xj,记为xi→xj。
定义6设xi,xj∈S(i≠j),若xi→xj且xj→xi,则称元素xi与xj有强连接关系。
定义7设S′⊆S,若∀xi,xj∈S(i≠j),xi与xj都有强连接关系,则称子系统S′为强连接的。
定义8设S′⊆S,若S′是强连接的,且∀xi∈S′,xj∈S-S′,xi与xj都无强连接关系,则称S′为系统S的强连接子集。

定义9设S的缩减系统为S′,则S′的可达矩阵称为S的缩减矩阵,记为R′e。


定义11设m阶布尔矩阵R′e为系统S的缩减矩阵,则S′k=R′e1/m-Im称为S的缩减骨架矩阵。对S′k进行缩减逆变换后得到的矩阵Sk称为S的骨架矩阵。
上述定义4~11主要根据文献[16]并参考文献[1,13]整理得到。
2 从拓扑分析到代数分析
文献[1,10]对现有的ISM方法作了介绍,从中可以看出,现有方法主要采用递归进行的逐层迭代方式进行划分操作,进而建立系统的结构模型。它类似于运筹学中常常用到的图上作业分析,是一种拓扑分析方法。当问题规模较小时,这种方法比较直观,易于理解,因而也就行之有效。
但对复杂系统而言,其内元素往往很多,并且元素间的关系错综交织,这样形成的问题规模就很大。如果沿用现有方法,一方面在计算复杂性上存在“组合爆炸”,从而导致问题求解的效率很低;另一方面逐层迭代的操作过程可能导致求解的不完备,下面以区域划分为例进行说明。
区域划分就是将系统从结构上划分成相互独立的若干部分,用公式可描述成
∏(S)={D1,D2,…,Dm}.
(6)
对于每一个元素xi,把xi可以到达的所有元素汇集成一个集合,称为xi的可达集R(xi);把所有的可以到达xi的元素汇集成一个集合,称为xi的前因集A(xi)。即
R(xi)={xj|xj∈S,rij=1},
(7)
A(xi)={xj|xj∈S,rji=1},
(8)
式中rij和rji均为可达矩阵的元素。
区域划分是自下而上实现的,首先找出满足
A(xi)=A(xi)∩R(xi)
(9)
的元素,经过分析可知,这样的元素一定是系统的底层元素,即其下不再有其他元素的元素。
将底层元素的集合记为B,对∀xi,xj∈B(i≠j),如果下式成立:
R(xi)∩R(xj)≠∅,
(10)
则xi和xj处于同一部分(区域)之内,否则它们就不在一个区域内。这一结论在系统工程的经典教材[1,11]都是这样表述的。
按照式(10)逐一分析,可以将系统中的元素归为不同的区域,从而实现区域划分。现有ISM方法断定满足式(10)的xi和xj在同一区域内,确实如此;但R(xi)∩R(xj)=∅,即不满足式(10)的xi和xj就不在一个区域内的结论则是不完备的,下面给出图3所示的反例。

图3 区域划分的一个反例
根据图3所示的系统,底层元素集B={1,2,3},从图3可以直观地看出,元素1,2,3在同一区域内。各元素的可达集是:R(1)={1,4},R(2)={2,4,5},R(3)={3,5}。按照式(10),R(1)∩R(2)={4}≠∅,所以1和2在同一区域内;R(2)∩R(3)={5}≠∅,所以2和3在同一区域内;由于区域划分满足传递性,所以元素1,2,3在同一区域内,这与直观的图形显示出来的结果一致。但是,R(1)∩R(3)=∅,按照现有ISM方法,1和3就不在一个区域内,显然这是不正确的,由此可见,现有ISM方法存在着不完备性。
上面剖析了现有ISM方法存在的问题,即求解大规模问题存在的“组合爆炸”和迭代操作存在的不完备性。要解决这些问题,就必须针对ISM的划分操作,将现有ISM的拓扑分析方法进一步转化为代数分析方法,以便计算机实施处理。从代数角度上讲,划分就是等价关系,它们有着本质的关系,乃是同一概念的不同表达形式。因此,基于代数分析的观点,划分的实质是要构造某种等价关系,该等价关系是相应划分的充要条件。这是文献[16]提出结构建模代数方法的基本出发点。
3 关于骨架矩阵的求法
结构建模形成的最终结构模型图中,哪些边要连上,哪些边不必连,是一个至关重要的环节。就现有ISM方法而言,对这一问题并未有效解决。实际上,现有方法对此问题采取的是回避方式,即仍然是运用拓扑分析、通过人为观察剔除派生连线来完成的,这种方式依赖于直觉,其正确性无法保证,弊端却是显而易见。
在结构建模代数方法求解中,这实际上是要确定系统的骨架矩阵(骨架矩阵的界定见定义11)。只有借助代数分析,给出骨架矩阵的代数表达式才能从根本上解决这一问题。因此,求系统的骨架矩阵是结构建模代数方法的另一个需要完成的任务。
为了获取骨架矩阵,文献[17]基于系统结构建模分析,给出了求骨架矩阵的代数表达式,实现了骨架矩阵的代数求法,从根本上解决了这一难题。该结果也是结构建模代数方法体系的组成部分。
4 结构建模中的矩阵关系分析
在第1节给出的概念定义的基础上,本节将进一步对系统结构建模进行分析,着重讨论ISM中涉及到的几种矩阵以及它们之间的相互关系,澄清认识,加深对结构建模实质的理解。
根据结构模型的定义,在论域明确的情况下,结构建模的目的主要是辨识关系R。若用D(R)表示R对应的有向图,那么在ISM中,D(S′k)就是缩减系统的结构模型,D(Sk)即是原系统的结构模型。
下面逐一讨论ISM中的各种矩阵的内涵并分析它们之间的关系。
设缩减骨架矩阵为m阶布尔矩阵,那么(S′k+Im)m=t(S′k+Im),又由定义11,(S′k+Im)m=R′e,所以
t(S′k+Im)=R′e,
(11)
若有S″k≠S′k,满足t(S′k+Im)=R′e,也即t(S″k+Im)=R′e,根据定义10和定义11,应有S″k>S′k,由式(11)可得
(12)
这说明D(S′k)保存了D(R′e-Im)的全部可达性,且具有最少的边,称为最少边图。因此,S′k反映的是缩减系统S′中元素之间的直接关系(从可达性讲,是一步可达关系)。同样,骨架系统Sk反映的是原系统S中元素之间的直接关系。
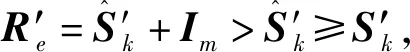
邻接矩阵A是由概念模型所描述的关系得到的,并且满足
Sk≤A≤Re,
(13)
它有两种特殊情况:A=Sk和A=Re。但通常A≠Sk,这是因为在复杂系统中,人们虽可判断元素之间是否存在关系,却往往难以区分哪些是直接关系,哪此是间接关系。而且通常也有A≠Re,原因在于人的观察能力有限,其判断并不总是保持传递性,尤其当系统元素较多时更是如此。即使邻接矩阵A等于Sk或者Re,要确认这一事实成立也非易事。一般来说,认为Sk 将上面讨论的各种矩阵的性质特征进行归纳,可总结得到表1。 表1 结构建模中各矩阵的性质 综合上述分析,可以明确得到以下结论: (1)不少文献(例如文献[18])在论述结构建模时认为邻接矩阵表示的是系统中各元素之间的直接关系。事实上,这一观点是不全面的。邻接矩阵不仅表示的是元素之间的直接关系,而且还表示了元素之间的部分间接关系,但不管是直接还是间接关系,它们都是相邻元素之间的关系。如果把元素对自身的零步可达关系看成是一种特殊的相邻元素(相邻元素重合)之间的关系,则邻接矩阵反映的就是不同元素之间的邻接联系情况,这样它才“名副其实”。 (2)在邻接矩阵的基础上求出可达矩阵,实质上是要找到系统元素之间的所有间接关系。根据可达矩阵得到的骨架矩阵只保留了元素之间的所有直接关系,这也是系统分析的通常作法,即把握那些本质关系,而忽略那些已被隐含的派生关系。 由Warfield提出并发展的解释结构建模(ISM)应用广泛,不乏成功案例[11-12]。该方法涉及邻接矩阵、可达矩阵等代数概念,但主要采用的是拓扑分析的思路,因此在求解大规模问题时存在着“组合爆炸”,在建模的迭代操作中存在着不完备性,这些不足导致现有ISM方法难以适应复杂系统结构建模的要求。针对现有ISM的拓扑分析方法的不足,有必要将现有ISM的拓扑分析方法进一步转化为代数分析方法,以便计算机实施处理。本文致力于复杂系统结构建模分析研究,一方面阐明适于复杂系统结构建模的代数分析途径的优越性,围绕复杂系统结构建模的几个重要问题剖析概念本质,进行原理性分析;另一方面着重讨论ISM中涉及到的几种矩阵以及它们之间的相互关系,澄清了一些容易混淆的观点和认识。 复杂系统结构建模是一个具有挑战性的难题,现有ISM的拓扑分析方法与本文倡导的代数分析方法相辅相成,可以取长补短,形成复杂系统结构建模的综合集成方法,据此下一步将开展综合集成视角下的复杂系统结构建模研究,提出相应的方法体系,实现复杂系统建模求解的大成智慧的涌现[19-20]。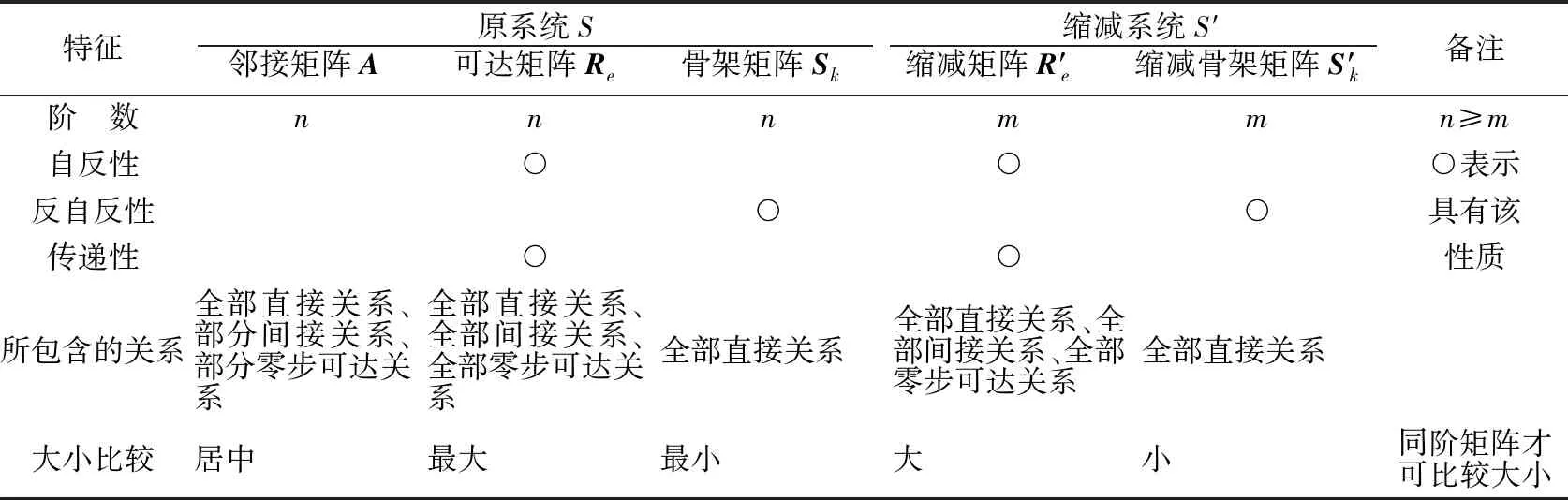
5 结束语

