AR（p）模型均值变点的CUSUM估计

许天明，魏岳嵩，张婷婷

（淮北师范大学 数学科学学院，安徽 淮北 235000）

0 引言

变点理论结合时间序列分析和数理统计的相关知识和研究方法，是数理统计学中非常重要的分支［1］. 变点理论最早由Page［2］提出，并用于解决产品生产的质量控制工程问题. 变点理论在金融、地质、计算机、统计、医学和气象等更多领域有全新的应用［3-5］.

变点的种类大致可分3 种：突变点、渐近变点及流行变点［6］. 对于AR 模型变点的理论研究，Gombay等［7］在Page的基础上将变点的在线监测模型问题推广至AR（p）模型中. 薛义新等［8］在Gombay的基础上，分析AR（p）模型参数变点的在线监测问题，得出参数的最小二乘估计量，确立参数变点的残差CUSUM监测统计量. 杨吉斌［9］用贝叶斯法研究AR（p）模型的变点估计问题和模型参数的贝叶斯估计问题. 李畅等［10］在杨吉斌的基础上先后利用极大似然法和贝叶斯估计法探讨AR（p）模型中的变点性质，并采用多元统计方法，得出变点位置估计的表达式. Pang等［11］对于AR（1）模型在未知时间附近参数可能发生结构突变时的渐近推断做系列研究，并用蒙特卡罗模拟证明估计量的有限样本性质. Venkatesan［12］分析AR（p）时间序列模型的方差可能在未知时间点发生多次变化，对于发生变化的未知时间点和模型参数，均发现后验分布. Qin 等［13］研究线性过程方差变化的强收敛速度，证明迭代法搜索方差变化较为有效. 张立文［14］对于AR（p）模型提出2种新型的估计法：门限自回归分位数复合估计法与分位数平均估计法. 对于AR模型变点的实际应用问题的研究，Cliff等［15］提出空间自回归模型的概念，并对模型进行参数估计与检验，周佳琪［16］在其基础上建立空间网络自回归模型，对合肥市住宅价格的空间变化进行分析.

基于以往的研究，AR（p）模型变点检测问题和实际应用问题的研究成果较多，对变点估计量理论性质研究较少. 本文主要讨论AR（p）模型均值变点的估计量的性质问题，假设只存在一个均值变点的情况下，讨论变点CUSUM估计量的相合性及其收敛速度.

1 模型构建

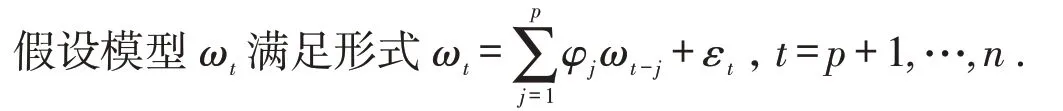
2 主要结论

由引理可知，对任意ε ＞0 和足够大的N可得

根据上式，只需证明当n→∞时，

故定理2得证.

3 结论

本文讨论AR（p）模型单均值变点CUSUM估计量的性质. 当n趋向于无穷大时，定理1证明估计量的强相合性，定理2给出估计量的强收敛速度. 但是在实际问题的处理中，变点个数往往不止一个，且可能同时存在多个均值和方差变点，下一步可以考虑推广至复杂的多变点情况，尝试得到更多结果.