一类带脉冲的分数阶中立型随机微分方程的平均值原理

侯婷婷，刘 燕

（安徽师范大学皖江学院 电子工程系，安徽 芜湖 241000）

0 引言

平均值原理的基本思想是用一个简单的系统来逼近原系统，即用相关的平均方程来研究复杂方程.平均值原理作为一种分析方法，被广泛地用来处理各种不同噪声下的随机微分方程（SDE），如泊松噪声和分数布朗运动噪声等.

从Khasminskii［1］的开创性工作开始，平均值原理就备受关注. Stoyanov 等［2］给出随机微分方程下经典的平均值原理. Abouagwa 等［3］在非Lipschitz 条件下建立对Itô-Doob 型分数阶SDE 的平均值原理；Xu等［4］则对Caputo分数阶SDE的平均值原理进行讨论. 同时受到噪声对系统的影响，Pei等［5］对由Brownian运动和分数布朗运动驱动的SDE进行研究；Xu等［6］在Lévy噪声驱动的随机动力系统中也得到相应的平均值原理；文献［7-11］讨论不同方程状态下带Lévy 噪声的平均值原理. 随机系统不仅依赖于当前和过去一段时间的状态，而且还和过去一段时间状态的变化率有关，由此开启对中立型泛函微分方程的研究［12-15］. 但是在现实生活中，许多随机现象还会受到脉冲的影响，即状态会在某些时刻发生突变，越来越多的学者对带脉冲的系统进行研究［16-18］. 目前尚未有文献对Lévy噪声驱动的带脉冲的分数阶中立型随机微分方程的平均值原理进行讨论. 因此，本文将重点研究该系统的平均值原理.

1 预备知识

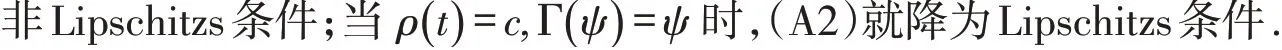
2 方程解的存在唯一性

3 平均值原理

设0＜ε1＜1,∀ε∈( 0,ε1],方程（1）的形式如下对于最后一项L5，由基本不等式得