聚焦椭圆学习中的易错点

崔胜峰

(邢台市第十九中学)

椭圆是圆锥曲线中的重要的曲线模型之一,历年高考中从未少过它的“身影”,高考中主要考查椭圆的方程、离心率及相关性质等,学生常常因为对椭圆方程掌握不够透彻,对椭圆的相关性质运用不够熟练而导致解题错误.本文主要对学生解题时的易错点进行分析,希望对读者有所帮助.

1 忘记讨论焦点位置

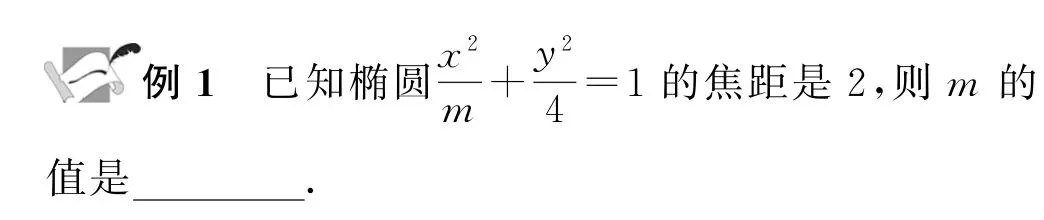
错解 由椭圆的方程可知a2＝m,b2＝4,则c2＝a2－b2＝m－4,而椭圆的焦距是2,即c＝1,所以m－4＝1,解得m＝5.

错因分析 在错解中,学生片面地认为x2下就是a2,y2下就是b2,即将此椭圆定性为焦点在x轴上的椭圆,事实上,本题中我们需要对m与4的大小进行讨论.

正解 当m＞4 时,a2＝m,b2＝4,则c2＝a2－b2＝m－4,而椭圆的焦距是2,即c＝1,所以m－4＝1,解得m＝5;当0＜m＜4时,a2＝4,b2＝m,则c2＝a2－b2＝4－m,而椭圆的焦距是2,即c＝1,所以4－m＝1,解得m＝3.

综上,m的值是5或3.

通过椭圆的标准方程,我们可以判断椭圆的焦点在哪条坐标轴上,对于不能确定分母值大小的椭圆方程,一定要对分母的大小加以讨论,以便准确确定椭圆焦点的位置.

2 对椭圆方程的理解不够透彻

解,整理得(m＋3)x2＋4mx＋m＝0,则Δ＝16m2－4m(m＋3)＞0,解得m＜0或m＞1.

3 忽视离心率范围

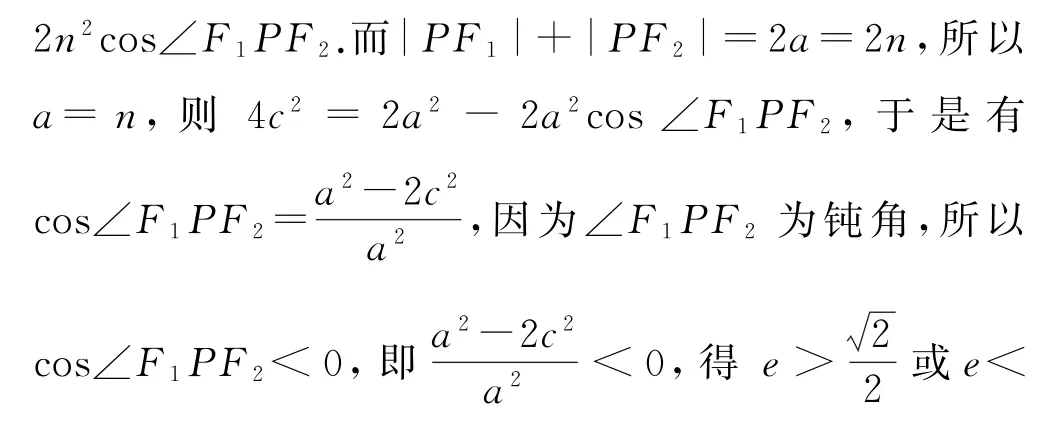
图1

图2

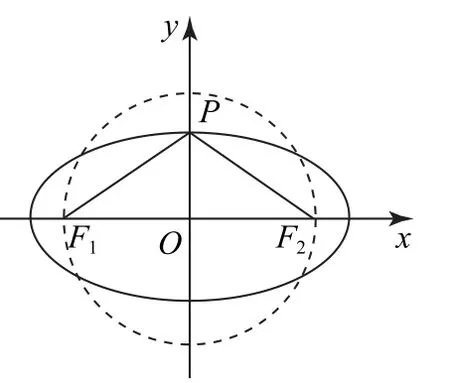
图3

离心率是椭圆的固有属性,其取值范围是(0,1),解离心率问题时,一定要牢记于心.本题的三种解析中,虽然解题思路不同,但要求得正确结论,都离不开对椭圆离心率取值范围的考虑.

4 未考虑椭圆上点的坐标范围

图4

椭圆是圆锥曲线中的常考曲线,在学习过程中,我们要对椭圆中的易错问题多分析、多思考、多总结,这样在考试时才能避免犯类似的错误.