同构法巧解圆锥曲线的双切线问题
林国红
(广东省佛山市乐从中学 528315)
过圆锥曲线外的一点可作两条圆锥曲线的切线,一般把此类涉及圆锥曲线的两条切线问题称之为圆锥曲线的双切线问题.这类问题一般涉及到双切线、双切点、双斜率等有关量,求解过程中的处理方法技巧性较强,对运算能力要求较高,是圆锥曲线的一个热点和难点问题.
本文通过典型例题赏析圆锥曲线双切线问题的优化解法——同构法,它在解决圆锥曲线双切线问题中常能达到化繁为简、举重若轻的效果.
1 两种解法比较
示例(2021年全国统一适应性考试(八省联考)第7题)已知抛物线y2=2px上三点A(2,2),B,C,直线AB,AC是圆(x-2)2+y2=1的两条切线,则直线BC的方程为( ).
A.x+2y+1=0 B.3x+6y+4=0
C.2x+6y+3=0 D.x+3y+2=0
解法1 (一般解法)因为A(2,2)在抛物线y2=2px上,故22=2p×2,即p=1,抛物线方程为y2=2x.
设过点A(2,2)与圆(x-2)2+y2=1相切的直线的方程为y-2=kx-2,即kx-y+2-2k=0.
则圆心2,0到切线的距离
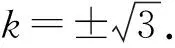
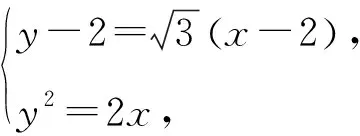
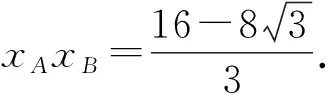
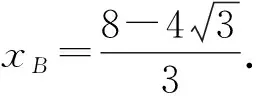

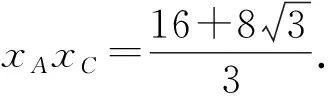

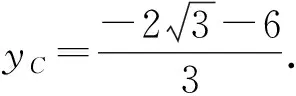
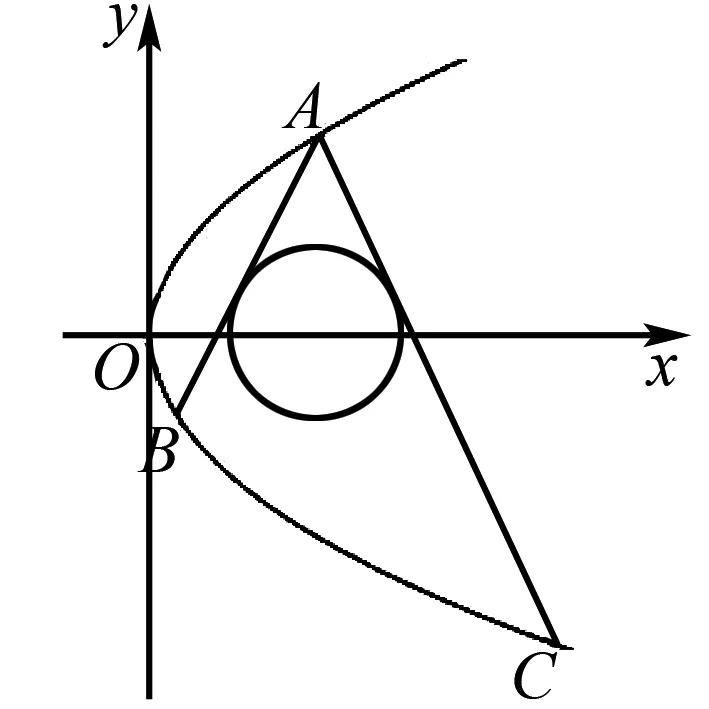
图1
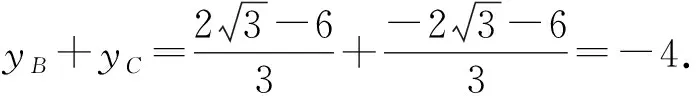
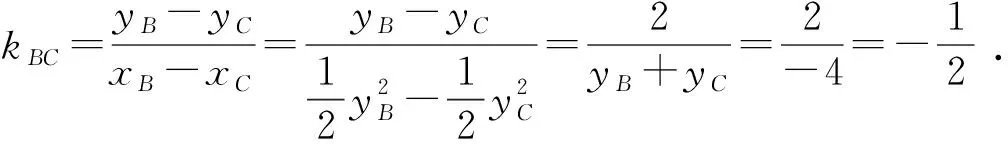
所以直线BC的方程为
即3x+6y+4=0.故选B.
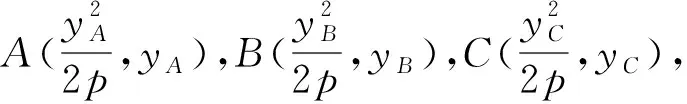
化简,得2px-(yA+yB)y+yAyB=0.
同理直线AC的方程为2px-(yA+yC)y+yAyC=0,直线BC的方程为2px-(yB+yC)y+yByC=0.
又因A(2,2),易得p=1,即得直线AB的方程为2x-(2+yB)y+2yB=0.
因为直线AB与圆(x-2)2+y2=1相切,
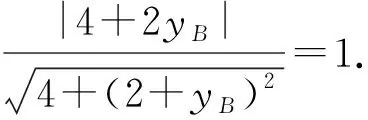
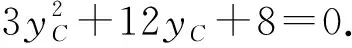

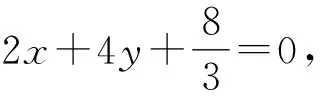
故选B.
解法3(同构解法)由解法2,可知点B,C的纵坐标yB,yC满足方程3y2+12y+8=0,考虑到点B,C的纵坐标yB,yC均满足y2=2x,从而可得6x+12y+8=0.
即3x+6y+4=0.
因为两点确定一条直线,所以直线BC的方程为3x+6y+4=0.故选B.
评注(1)示例的解法1容易想到,但运算量较大,费时耗力,容易算错,解法2与解法3的同构法中代数变形较为简单,整体替换、设而不求,运算量较少,解题过程更为简洁.
(2)同构式是指除了变量不同,结构与形式都相同的代数式.同构化的解题思想在高中数学中有着重要的地位,在圆锥曲线中也应用广泛.一般来说,同构法解答圆锥曲线双切线问题的步骤如下:
①过曲线外一点(x0,y0)设曲线的切线方程为y=k(x-x0)+y0;
②联立切线与曲线方程消元,得Δ=0或圆心到切线的距离d=r(圆的切线);
③将Δ=0(或d=r)整理成以k为主元的二次方程,则k1,k2为方程的两个根(同构思想);
④由韦达定理得k1+k2,k1k2;
⑤根据题目条件进一步求解.
2 同构法在圆锥曲线双切线问题中的应用
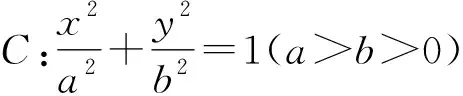
解析当过点P的两条切线一条斜率不存在,另一条斜率为零时,这样的点P有四个,分别是(a,b),(-a,b),(a,-b),(-a,-b),显然这四个点都在圆x2+y2=a2+b2上.
当切线PA,PB的斜率均存在时,设过点P(x0,y0)与椭圆相切的方程为y=k(x-x0)+y0.
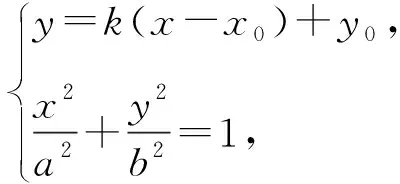
(b2+a2k2)x2+2a2k(y0-kx0)x+a2(y0-kx0)2-a2b2=0.
因为直线与椭圆相切,所以Δ=0.
整理成关于k的方程
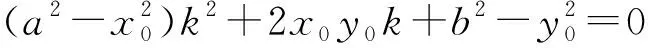
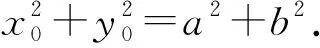
综上,交点P的轨迹方程为x2+y2=a2+b2.
例2 (2021年全国甲卷理20)抛物线C的顶点为坐标原点O,焦点在x轴上,直线l:x=1交C于P,Q两点,且OP⊥OQ.已知点M(2,0),且圆M与l相切.
(1)求C,圆M的方程;
(2)设A1,A2,A3是C上的三个点,直线A1A2,A1A3均与圆M相切.判断直线A2A3与圆M的位置关系,并说明理由.
解析(1)抛物线C的方程为y2=x,圆M的方程为(x-2)2+y2=1.
(2)若A1A3⊥x轴,且A1A3与圆M相切,则直线A1A3的方程为x=3.
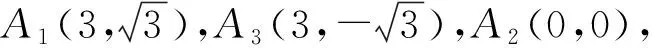
当直线A1A2,A1A3均存在斜率时,设A1(a2,a),A2(b2,b),A3(c2,c),则直线A1A2的方程为
即x-(a+b)y+ab=0.
同理直线A1A3,A2A3的方程分别为
x-(a+c)y+ac=0,x-(b+c)y+bc=0.
因为直线A1A2,A1A3与圆M相切,于是
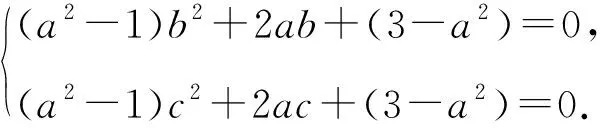
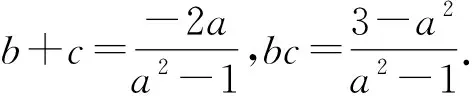
于是圆心M到直线A2A3的距离
故直线A2A3与圆M相切.
综上,直线A2A3与圆M相切.
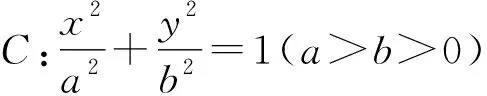
(1)求椭圆C的方程;

图2
(2)如图2,设R(x0,y0)是椭圆C上的一动点,由原点O向圆(x-x0)2+(y-y0)2=4引两条切线,分别交椭圆C于点P,Q.若直线OP,OQ的斜率均存在,并分别记为k1,k2,求证:k1·k2为定值;
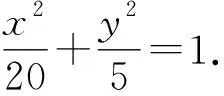



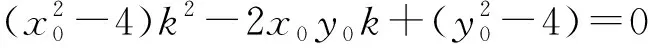
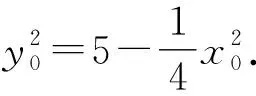
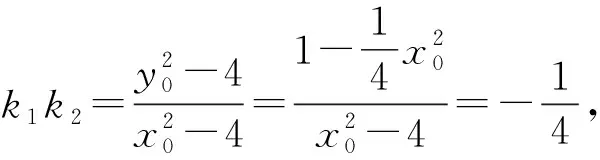
例4 (2011年浙江卷理21)已知抛物线C1:x2=y,圆C2:x2+(y-4)2=1的圆心为点M.
(1)求点M到抛物线C1的准线的距离;
(2)已知点P是抛物线C1上一点(异于原点).过点P作圆C2的两条切线,交抛物线C1于A,B两点,若过M,P两点的直线l垂直于AB,求直线l的方程.
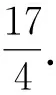
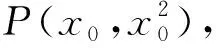
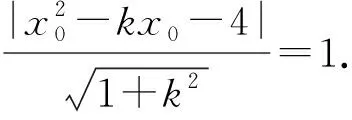
整理,得


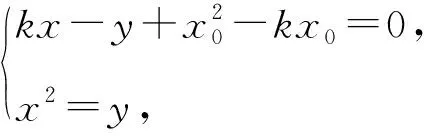
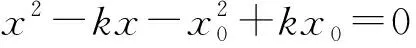
故有x0+x1=k1.即x1=k1-x0.
同理有x2=k2-x0.
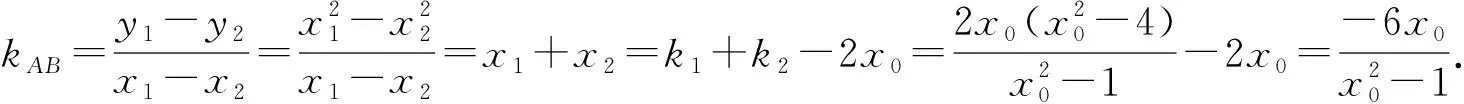
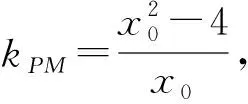
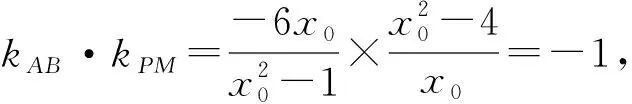


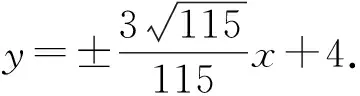
圆锥曲线的双切线问题往往需要具备较强的知识综合性,较高的思维能力与运算能力,而同构法可以将此类问题统一处理,是一种通性解法,能降低思维强度,简化推理证明过程,具有直观、简捷的特点.同构转化的解题思想能发现数学的结构共性的意识,以及利用结构共性解题的思维导向,这正是高中数学新课标核心素养中不可或缺的重要内容.

