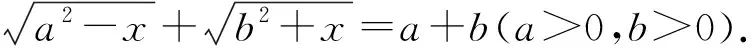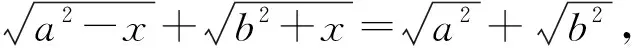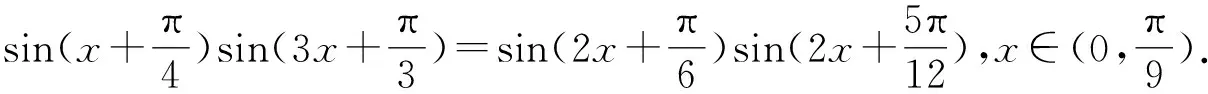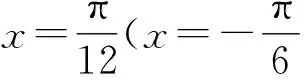破解一类无理方程问题的新视角
——导数
张 君
(四川省温江中学 611130)
1 预备知识
引理1拉格朗日中值定理.
若函数f(x)满足如下条件:
(1)f(x)在闭区间[a,b]上连续;
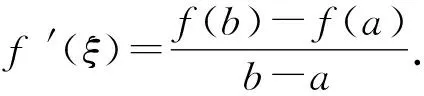
引理2琴生(Jensen)不等式.
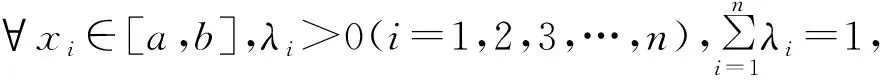
反之,若f(x)为严格凸函数,则有
f(λ1x1+λ2x2+…+λnxn)≥λ1f(x1)+λ2f(x2)+…+λnf(xn).
当且仅当x1=x2=…=xn时等号成立.
引理3 设f(x)是区间I上的二阶可导函数,则在I上f(x)为严格凸(凹)函数的充要条件是f″(x)<0(f″(x)>0).
2 一类无理方程问题
问题2 解方程log3(x-5+6)·log3(x2+3)=log37·log3(x2+x-5+2).
观察以上三个问题,不难发现:
(2x2+x+11)+4=(x2+3)+(x2+x+12),
x-5+6+(x2+3)=7+(x2+x-5+2).
由此可见,以上两个问题均是以“f(x)+g(x)=h(x)+k(x)”为背景,求无理方程F(f(x))+F(g(x))=F(h(x))+F(k(x))或者F(f(x))·F(g(x))=F(h(x))·F(k(x))的解问题.这一类问题并不是很好处理,笔者尝试从导数的视角去研究破解此类问题的方法.
3 探究问题的破解之道
定理1 若函数F(x)在区间
F(f(x))+F(g(x))=F(h(x))+F(k(x))
(1)
与f(x)=h(x)或f(x)=k(x)
(2)
同解.
注符号< >表示开区间、闭区间、半开区间、半闭区间、有限区间或无限区间.若F″(x)>0(F″(x)<0),则要求使得等号成立的点只有有限个,即F(x)是严格凹(凸)函数.下同.
证明这里仅证明F″(x)>0情形(F″(x)<0情形类似可证).
设x0是f(x)=h(x)的一个根,即
f(x0)=h(x0).
又f(x0)+g(x0)=h(x0)+k(x0),
从而g(x0)=k(x0).
于是F(f(x0))+F(g(x0))=F(h(x0))+F(k(x0)).
即x0是方程(1)的根.
设x0是方程(1)的根,证明x0也是方程(2)的根,用反证法.
假设x0不是方程(2)的根,即x0不是f(x)=h(x)和f(x)=k(x)的根,则只能有以下四种情形:
①f(x0)>h(x0),f(x0)>k(x0);
②f(x0) ③f(x0)>h(x0),f(x0) ④f(x0) 这里仅证情形①(其他情形类似可证),由已知条件,有 f(x0)-h(x0)=k(x0)-g(x0)=d>0, 从而f(x0)=h(x0)+d与k(x0)=g(x0)+d. 设u(x)=F(x+d)-F(x),x∈ 由引理1及F″(x)>0,有u′(x)=F′(x+d)-F′(x)=F″(ξ)d>0,ξ∈(x,x+d). 所以函数u(x)在 由情形①知h(x0)>g(x0). 所以u(h(x0))>u(g(x0)). 从而F(h(x0)+d)-F(h(x0))>F(g(x0)+d)-F(g(x0)). 即F(f(x0))+F(g(x0))>F(h(x0))+F(k(x0)). 即x0不是方程(1)的根,矛盾. 问题1的解将方程变形为 由定理1知,原方程与方程x2+x+12=4或x2+3=4同解.解之得x1=-1,x2=1,代入原方程验证均为原方程的根. 定理2 若函数F(x)在区间 F(f(x))·F(g(x))=F(h(x))·F(k(x)) (3) 与f(x)=h(x)或f(x)=k(x) (4) 同解. 证明仅证F″(x)<0,F(x)>0情形(F″(x)>0,F(x)<0情形类似可证). 设x0是方程(4)的根,即f(x0)=h(x0)或f(x0)=k(x0). 由已知条件,有 f(x0)+g(x0)=h(x0)+k(x0). 从而g(x0)=k(x0)或g(x0)=h(x0). 于是F(f(x0))·F(g(x0))=F(h(x0))·F(k(x0)),即x0是方程(3)的根. 设x0不是方程(4)的根,即x0既不是方程f(x)=h(x)的根,也不是方程f(x)=k(x)的根,则共有以下四种情形. ①f(x0)>h(x0),f(x0)>k(x0); ②f(x0) ③f(x0)>h(x0),f(x0) ④f(x0) 这里仅证明情形①(其他情形类似可证),由已知条件,有 f(x0)+g(x0)=h(x0)+k(x0). 从而f(x0)>h(x0). 由f(x0)-h(x0)=k(x0)-g(x0)>0, f(x0)-k(x0)=h(x0)-g(x0)>0, 已知F″(x)<0(即F(x)为严格凸函数),F(x)>0,f(x0)≠g(x0). 由琴生不等式,有 F(h(x0))·F(k(x0)) =F(f(x0))·F(g(x0)) 即x0不是方程(1)的根.证毕. 由定理2知,原方程与方程x-5+6=7或x-5+6=x2+x-5+2同解.解之得x1=6,x2=4,x3=2,x4=-2,代入原方程验证均为原方程的根. 由定理1知,原方程与方程a2-x=a2或a2-x=b2同解.解之得x1=0,x2=a2-b2,代入原方程验证均为原方程的根. 解析设函数F(x)=sinx,x∈(0,π),则F″(x)=-sinx<0,F(x)=sinx>0.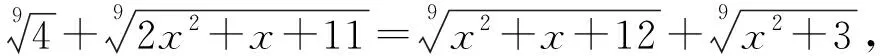
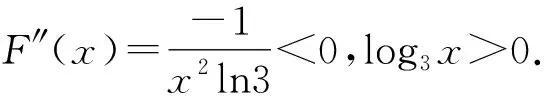
4 变式训练