基于混合模型的超短期风速区间预测

张金良，刘子毅

基于混合模型的超短期风速区间预测

张金良，刘子毅

(华北电力大学经济与管理学院，北京 102206)

准确的风速预测能够促进大规模的风电并网，保证电力系统的安全稳定运行。针对传统点预测方法难以表征预测结果概率可信度问题，提出一种基于模糊信息粒化、改进长短期记忆网络与差分自回归移动平均模型的混合区间预测模型。首先，采用自适应噪声的完全集合经验模态分解模型对原始风速数据进行分解，并依据模糊熵重构得到新序列。在此基础上，对每个序列依次进行模糊信息粒化，获得最大值、最小值及平均值。最后，利用改进长短期记忆网络模型预测高频序列，差分自回归移动平均模型预测低频序列与余项，并将所得上下界求和得到最终风速区间。算例分析表明，所提模型得出的风速预测区间能够准确覆盖实测风速，为电力系统调度提供更多有价值的决策信息。

风速区间预测；模糊信息粒化；改进长短期记忆神经网络；差分自回归移动平均模型；混合模型

0 引言

随着人民生活水平的提高以及用能的电气化趋势，“十四五”期间全社会用电量将保持稳步增长的态势。电力生产清洁化是实现碳中和的关键路径之一，而风电作为一种发展迅速的可再生清洁能源可较好地承接火电来满足电力增量需求。近年来，风电装机容量不断增大，大规模风力发电并网输送，自然风的随机性与波动性对电网的影响也愈加突出。对风速的预测可以保障风电机组的稳定运行，帮助调度人员优化决策方案，在提升电网安全可靠性的同时增加了风电场的经济效益。因此，风速预测是具有重大意义的研究热点。

现阶段风速点预测模型可归为3种，第1种为考虑数值天气预报的物理模型。文献[1]根据ECMWWF-NWF模型预测未来72 h的风速。文献[2]用集成的模型预测未来48 h的风速。文献[3]结合NWP和ARIMA模型预测每天的风速。文献[4]采用卡尔曼滤波和NWP预测每小时的风速。由于气象因子数据更新较慢，在短时间内难以获取，故物理模型不适合超短期风速预测，因此，提出了第2种统计预测模型。文献[5]改进了ARIMA的参数，从而提升了风速预测的准确度。文献[6]建立ARIMA- GARCH模型，实现了对超短期风速的快速预测。文献[7]使用自回归积分滑动平均模型预测爱尔兰某风电站的风速，取得了良好的预测结果。传统的统计模型对线性数据具有较好的预测效果，然而，在实际应用中，风速时间序列是不平稳的，所以仅用线性的统计模型无法满足要求。故提出第3种结合人工智能算法的混合模型。文献[8]将VMD算法与LSTM网络结合实现对风速的超前一步预测。文献[9]提出的基于优化的DBN模型提高了滨海风电场风速的预测精度。文献[10]采用深度卷积神经网络和双向门控循环单元，分别提取对自然风产生影响的时空特征，并利用融合后的特征进行风速预测，通过实例验证了算法的有效性。文献[11]将小波分解后的风速数据输入神经网络中，获得精度较高的风速预测结果。

上述研究采用不同技术获得风速的点预测结果，各模型均有不同特点且预测效果优良。然而，仅获得点预测值仍存在两点不足：1) 受内外条件、数据及模型等多方面的影响，使得点预测结果难免存在误差；2) 确定性的点预测结果无法描述预测值的变化范围，这为调度管理人员做最优决策带来了较大困难。为了给系统调度人员提供更多有利于决策的信息并规避风险，研究逐渐延伸到对风速的区间进行预测。文献[12]以点预测为基础，根据核密度估计的概率分布构造风速区间。文献[13]在数据处理后采用混合模型得到点预测值，并采用ARIMA和改进的一阶马尔可夫链模型对风速进行概率区间预测。文献[14]利用Fourier函数拟合误差概率分布，根据点预测结果估计风速区间。结合统计学的方法进行参数估计，虽可降低模型构造的复杂度，但假设数据序列满足的某种分布与实际分布具有偏差，有产生较大拟合误差的可能。为此，提出了人工智能算法进行区间预测，其中一类方法仅应用神经网络进行区间预测。文献[15]根据误差来训练样本预测区间的上下界，并依据目标准则不断更新，获得最优区间。文献[16]基于机器学习方法和多目标优化算法对风速序列进行建模预测。文献[17]提出了一种新的基于时间卷积网络的风速区间预测模型。另一类方法是基于模糊信息粒化与神经网络算法来构造区间模型。文献[18]基于模糊信息粒化和最小二乘支持向量机提出了一种短期风速区间预测算法，用于预测风电场短期风速的变化区间和变化趋势。文献[19]应用模糊信息粒化和灰狼优化-支持向量机算法建立了风速预测模型，提高了风速范围预测的效果。文献[20]提出了一种基于模糊信息粒化和长短期记忆网络的动态预测模型，可描述风速波动性的区间预测结果。文献[21]提出了一种经验小波变换模糊信息粒化和变异鲁棒极限学习机组成的短期风速区间预测模型。尽管人工智能算法有效地弥补了参数估计方法存在的缺陷，但由于风速的复杂特性，单一的人工智能算法对区间预测的研究仍存在一定的局限。考虑到风速原始数据具有多种特性，预先对风速原始数据进行分解处理，再结合优化的神经网络算法进行区间预测，可增强所获区间的可靠性。文献[22]采用变分模态分解对原始风速序列分解，并基于样本熵进行重构，对新序列采用相关向量机算法分别建立预测模型。文献[23]基于局部均值分解-模糊熵和混合灰狼算法优化学习机构建短期风速区间预测模型。文献[24]提出了经验模态分解法与飞蛾火焰算法改进高斯过程回归法相结合的模型，预测短期风速区间。文献[25]提出了一种将变分模式分解和低秩多核岭回归(MKRR)相结合的混合预测方法，用于短期风速区间预测。

综上所述，本文提出“分解-重构-粒化-预测”的思路，采用混合模型进行超短期风速区间预测。

由于自适应噪声的完整集合经验模态分解(complete ensemble empirical mode decomposition with adaptive noise, CEEMDAN)具有更快的计算速度与更好的分解结果，将其确定为原始风速序列的分解方法。而模糊熵值能够随参数的调整而稳定变化，性能较好，故利用模糊熵值对分解得到的多个序列进行重构。其次，应用模糊信息粒化处理每个重构的新序列，获得最大值、最小值和平均值。模糊信息粒化可对样本数据进行特征提取，是构造区间上下界的基础。最后，应对不同特征的粒化结果建立一个合适的模型。风速受其历史数据的影响，一些分量会表现出规律性的特征。因此，将差分自回归移动平均模型(autoregressive integrated moving average model, ARIMA)应用于常规分量预测。此外，风速也会受到随机因素的影响，其他分量呈现不规则特征。对于不规则分量，人工神经网络具有良好的非线性拟合能力和自适应能力，为解决传统人工神经网络存在过拟合和梯度消失的问题，提出改进长短期记忆网络进行预测。两部分结果加总得到最终的预测区间。

1 基本理论

1.1 自适应噪声完全集合经验模态分解

考虑到经验模态分解方法存在模态混叠的缺陷，导致信号分解精度不高，提出了集合经验模态分解方法。然而，集合经验模态分解仍存在计算量较大、具有冗余噪声等问题。为了进一步优化集合经验模态分解，文献[26-27]提出了基于自适应噪声的完整集合经验模态分解。CEEMDAN技术方法有两个优势特征：1) 此方法是一种自适应的信号处理方法，可将数据序列分为有限且不同时间尺度的分量；2) 在原始信号中添加一组符号相反的白噪声，解决了前两种方法存在的缺陷。CEEMDAN分解的原理如下所述。

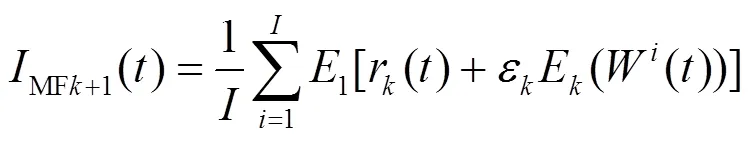
残差最终结果为

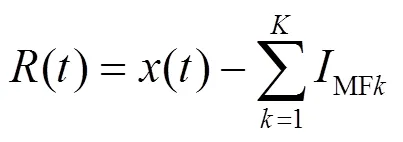
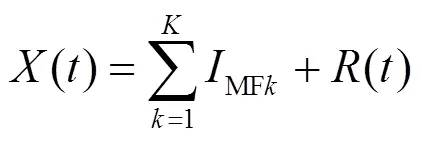
1.2 模糊熵

模糊熵(fuzzy entropy, FE)是一种度量时间序列复杂程度的方法。该方法基于模糊集的概念，应用指数函数将向量的相似性作为模糊化度量，使模糊熵值能够随参数的调整而稳定变化，是近似熵与样本熵的优化。模糊熵算法的具体步骤如下所述。

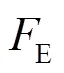
1.3 模糊信息粒化

模糊化过程本质是确定一个函数的过程，是模糊概念G的隶属函数。本文采用三角型模糊粒子，隶属函数表示为

1.4 差分自回归移动平均模型

1.5 改进的长短期记忆神经网络

由于LSTM的拟合效果取决于学习率，为此本文利用鲸鱼优化算法(whale optimization algorithm, WOA)对其进行优化。该方法调参简单，易于跳出局部最优解，相比传统优化方法具有优越性。鲸鱼优化算法包括3个阶段：1) 包围猎物；2) 狩猎行为；3) 搜索猎物。鲸鱼采用随机的方式来分析其他鲸鱼的位置并搜索猎物，以随机选择的值代替最优结果。这种探索的方式保证鲸鱼算法具有更好的全局搜索能力，可找到全局最优解。数学表达式为

2 预测方法

本文应用分解重构的思路对风速原始数据进行处理，并通过优化的长短期记忆网络与ARIMA对模糊信息粒化结果进行预测，获得预测区间，预测流程如图1所示。具体流程分为以下3步。

图1 超短期风速区间预测流程

1) 对原始风速数据进行CEEMDAN分解，得到若干组具有不同特征的子序列，再计算各子序列的模糊熵值，对子序列进行重构得到新的序列。

2) 将此时所得到的个重构序列分别进行模糊信息粒化处理，获得组最小值(LOW)、最大值(UP)和平均值(R)数据，并归一化处理。

3) 使用鲸鱼优化算法改进的长短期记忆网络(WOA-LSTM)模型(或称为ILSTM，“I”为“improved”的首字母，代表改进的长短期记忆网络，指代WOA-LSTM)与ARIMA模型分别对具有不同特性的重构序列的LOW、UP、R进行预测，得到若干组区间上下限与反应区间趋势的值，将所有区间加总求和得到最终的超短期风速区间结果。

3 算例分析

本文所用风速数据源于美国国家风能技术中心(national wind technology center, NWTC)风速观测站。选取NWTC站2019年12月25日的实测风速数据，每1min作为一个采样点，总样本量为1440，原始风速数据如图2所示。另外，从爱荷华州立大学官网获得美国某风电场的风速数据，便于对比研究。以下实验仿真在Matlab R2018a与Eviews10.0 (x64)平台上实现。

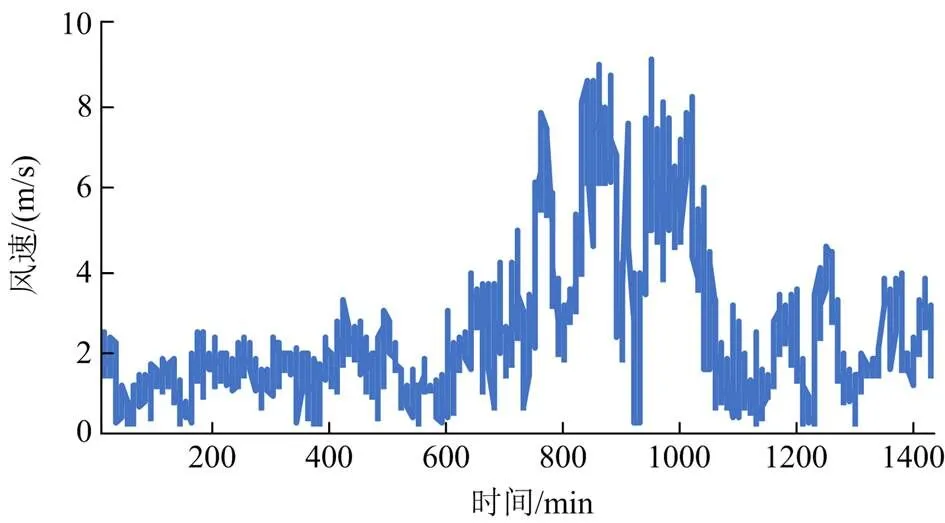
图2 原始风速数据

通过调研已有的研究发现，评价超短期风速预测区间需要考虑两个关键点：1) 区间的可靠性；2) 区间的清晰度。实际值落入区间的个数越多代表区间的可靠性越强，通常以覆盖率作为指标来反映区间的可靠性。在一定条件下区间宽度越小则清晰度越高，故以区间宽度作为指标来衡量区间的清晰度。本文通过上述指标来评价区间结果的优劣，指标具体介绍如下。

1) 预测区间覆盖率(prediction interval coverage probability, PICP)代表真实值落在预测区间的概率。PICP越大，预测区间所包含的真实值越多，区间的可靠越强。其公式为

2) 预测区间平均宽度(prediction interval normalized average width, PINAW)表示区间结果的宽窄，由于单纯追求高的区间覆盖率而导致较大的宽度使得预测区间失去了意义，故增添平均宽度作为另一个衡量指标，其公式为

3) 预测区间均方根宽度(prediction interval normalized root-mean-square width, PINRW)是基于PINAW获得的评价宽度的指标，从均方根的角度刻画区间宽度，其公式为

3.1 数据处理

首先应用CEEMDAN对原始风速数据进行分解，获得原始信号中具有不同特征的分量，CEEMDAN分解结果如图3所示。

图3 CEEMDAN分解结果

然后计算各分量的模糊熵值。其中，嵌入维数取2，相似容忍度取0.2，权重取1。模糊熵反映数据序列的复杂程度，模糊熵值越大代表数据越复杂，其非线性越强。CEEMDAN分解所获各序列模糊熵值及趋势如图4所示。

图4 CEEMDAN分解所获各分量模糊熵值及趋势

由图4可得，模糊熵值分布在[0,0.02]、[0.1,0.5]和[2,4]，基于这3个范围将各分量重新组合，重组结果如表1所示。

表1 分解重构结果

3个新序列的重构结果如图5所示，新序列1与新序列2分别具有明显的高频特征和低频特征，新序列3单独作为重组序列的余项，反映了风速数据波动的大致趋势，避免了信息丢失，最终得到具有不同特性的3个子序列。通过分解重构既避免了分解结果冗余，又防止了丢失信息，为随后的预测建立数据基础。

图5 重构结果

将3个子序列分别进行模糊信息粒化处理，以5个采样点(5 min)为一个窗口，每个分量均可提取出区间下限、均值和区间上限。图6—图8依次为新序列1到新序列3的粒化视图。

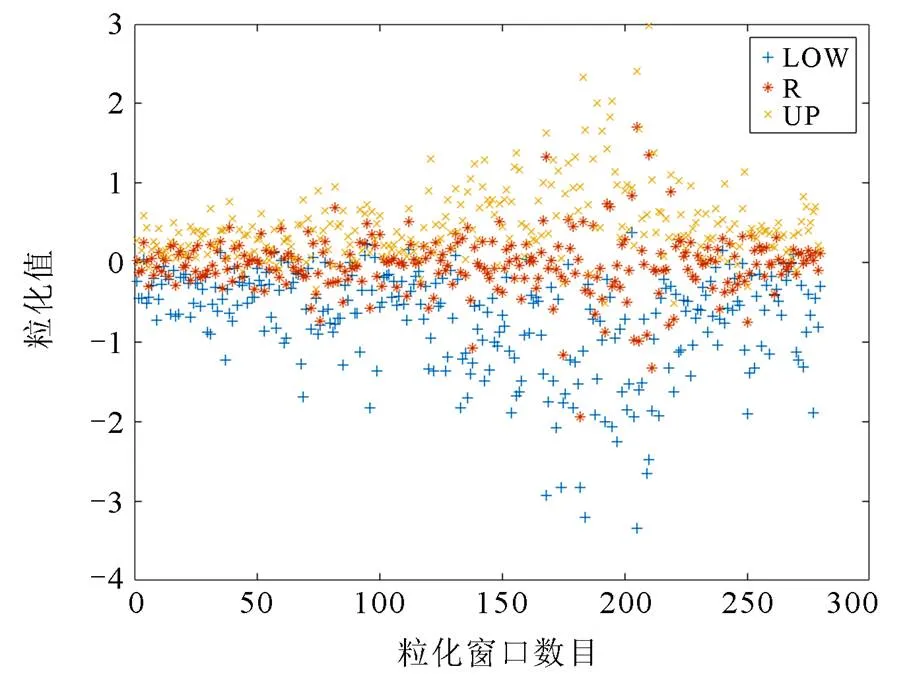
图6 新序列1的粒化视图

图7 新序列2的粒化视图

图8 新序列3的粒化视图

3.2 区间预测

本文组合神经网络模型与时间序列模型完成区间预测。在构建优化的LSTM模型方面，利用新序列1进行训练，分别取图6中LOW、UP的共288 min数据，其中前230 min数据作为模型的训练样本，后58 min数据作为模型的测试样本。设置鲸鱼算法与长短期网络的基本参数，将均方根误差作为鲸鱼算法的适应度，得到鲸鱼优化的长短期记忆网络模型。基于此模型进行预测，分别得到区间下界与区间上界的预测结果。同时，根据粒化后的数据(新序列2、新序列3)构建ARIMA模型，将数据输入ARIMA模型得到区间上下界的预测结果，全部结果加总求和得到总预测区间，如图9所示。

根据图9，风速实际值基本在预测区间的上下界内，且带状区间的趋势与实际值的趋势大致相同，表2展示了图9对应的区间结果。

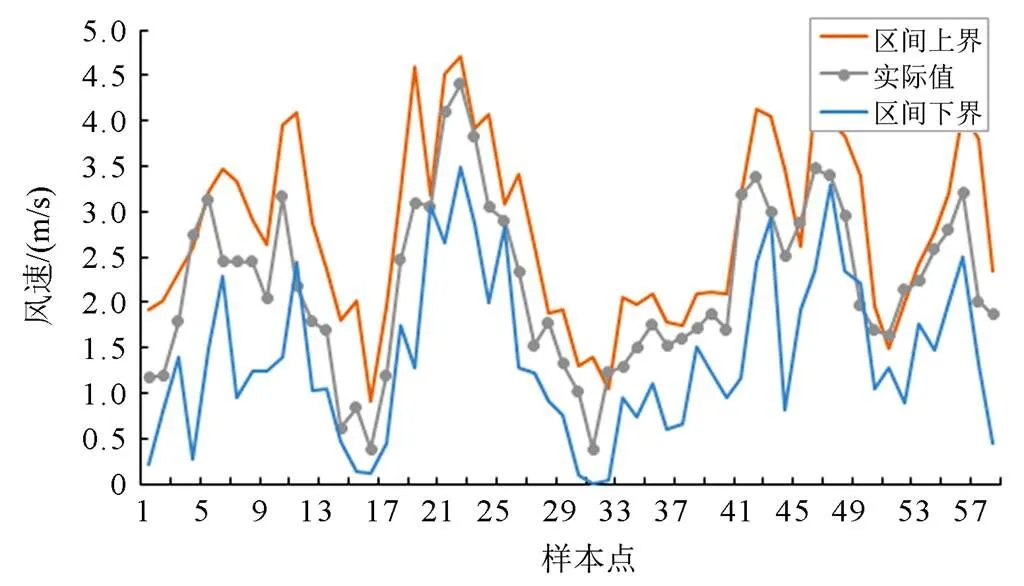
图9 FIG-ILSTM-ARIMA模型预测区间示意图

表2 FIG-ILSTM-ARIMA模型区间预测结果

3.3 结果分析

为进一步验证所提模型构造区间的优越性，分别对3种场景的指标进行对比分析，如表3—表5所示。其中：表3展示了采用不同模型对不同季节的风速进行区间预测的评价结果；表4比较了不同风场下各模型预测区间效果的优劣；表5对比了不同模型在极端风速情景下的区间构造情况。总体而言，覆盖率变大，区间宽度随之变窄，体现了所提模型构造区间的优势。虽然出现对照方法的区间宽度比所提模型的宽度略小的现象，但从综合覆盖率的指标来看，当区间宽度结果相差不多时，所提模型的覆盖率比对照方法的覆盖率大很多。因此，通过3种情景指标的整体对比可验证所提模型预测的风速区间具有可靠性，以下对不同情景的结果进行逐一分析。

表3 不同方法下四季风速区间评价指标对比

根据表3，纵向对比不同季节任选一天的风速区间评价指标可发现，所提模型具有较高的覆盖率，依次为93.10%、91.38%、91.38%和89.66%，全部大于对照方法的覆盖率，这是由于对照方法在信息粒化前均未进行分解重构与特征判断，导致预测效果不佳。横向对比某一天的指标计算结果，所提模型具有较高的覆盖率与较窄的区间宽度，区间更具可靠性。

根据爱荷华州立大学官网的风速数据，计算得到表4。通过对比不同风场的预测结果，所提模型在其他风场仍具有良好的区间预测性能，区间结果如图10所示。

表4 不同风场的单日风速区间预测评估对比

图10 FIG-ILSTM-ARIMA模型LOWA风场预测区间示意图

表5 尖峰风速区间预测评估对比

取NWTC的尖峰数据对极端风速情景的区间预测性能进行研究，通过与基准模型的不同指标对比，可验证此方法在极端风速情景下仍适用。单独分析表3中7月8日的风速，可发现所提模型在7月8日的指标结果最优，覆盖率与区间宽度分别为91.38%和23.83%，原因是此日的风速具有很明显的尖峰性，这体现出所提模型对于尖峰数据的预测优势，对具有强波动的数据预测仍有很好的适用性，尖峰风速区间结果如图11所示。

图11 FIG-ILSTM-ARIMA模型尖峰风速预测区间示意图

4 结论

相比传统点预测，区间预测可为管理决策提供更多有效信息。本文基于信号分析、信息粒化、神经网络以及时间序列预测方法，建立了一种混合模型来描述超短期风速的波动范围，并利用实际风速数据进行预测研究，主要研究结论如下：

1) 应用自适应噪声完全集合经验模态分解与模糊熵相结合的方法实现了对历史风速数据的分解和重构，在规避过多分量而导致计算复杂的同时实现了对信号特征的充分提取，为获得优良的区间预测效果建立了坚实基础。

2) 通过特征判断将重组序列分成高低频与残差，残差单独作为一组序列来反映风速数据波动的大致趋势，保证信息的完整性。根据新序列的不同特征，分别运用ILSTM与ARIMA进行针对性的预测，充分发挥多种算法的优势，提升预测效果，所构区间在尖峰风速下仍具有良好的覆盖性。

3) 模糊信息粒化方法可对风速数据进行挖掘并提取所需的有效信息，利用ILSTM处理高频的非线性特征较强的数据，采用ARIMA处理低频与趋势特征明显的数据。将3种算法结合来实现对风速波动范围的预测，可同时保证较高的覆盖率和较窄的区间宽度，为风速区间预测提供了一种可靠、适用的方法。

[1] ALESSANDRINI S, SPERATI S, PINSON P. A comparison between the ECMWF and CCOSMO ensemble prediction systems applied to short-term wind power forecasting on real data — DTU Orbit (30/05/15)[J]. Energy, 2013, 107: 271-280.

[2] DEPPE A J, GALLUS W A, TAKLE E S. A WRF ensemble for improved wind speed forecasts at turbine height [J]. Weather Forecast, 2013, 28: 212-228.

[3] FELICE M D, ALESSANDRI A, RUTI P M. Electricity demand forecasting over Italy: potential benefits using numerical weather prediction models[J]. Electric Power Systems Research, 2013, 104: 71-79.

[4] LYNCH C, OMAHONY M J, SCULLY T. Simplified method to derive the Kalman filter covariance matrices to predict wind speeds from a NWP model[J]. Energy Procedia, 2014, 62: 676-685.

[5] AMINI M H, KARGARIAN A, KARABASOGLU O. ARIMA-based decoupled time series forecasting of electric vehicle charging demand for stochastic power system operation[J]. Electric Power Systems Research, 2016, 140: 378-390.

[6] 丁藤, 冯冬涵, 林晓凡,等.基于修正后ARIMA- GARCH模型的超短期风速预测[J]. 电网技术, 2017, 41(6): 1808-1814.

DING Teng, FENG Donghan, LIN Xiaofan, et al. Ultra- short-term wind speed forecasting based on improved ARIMA-GARCH model[J]. Power System Technology, 2017, 41(6): 1808-1814.

[7] SINGH S N, MOHAPATRA A. Repeated wavelet transform based ARIMA model for very short-term wind speed forecasting[J]. Renewable Energy, 2019, 136: 758-768.

[8] 王俊, 李霞, 周昔东, 等. 基于VMD和LSTM的超短期风速预测[J]. 电力系统保护与控制, 2020, 48(11): 45-52.

WANG Jun, LI Xia, ZHOU Xidong, et al. Ultra short term wind speed prediction based on VMD-LSTM[J]. Power System Protection and Control, 2020, 48(11): 45-52.

[9] 王硕禾, 张嘉姗, 陈祖成, 等. 基于改进深度信念网络的风电场短期风速预测[J]. 可再生能源, 2020, 38(11): 1489-1494.

WANG Shuohe, ZHANG Jiashan, CHEN Zucheng, et al. Short term wind speed forecasting of wind farm based on improved deep belief network[J]. Renewable Energy Resources, 2020, 38(11): 1489-1494.

[10] 凡航, 张雪敏, 梅生伟, 等. 基于时空神经网络的风电场超短期风速预测模型[J]. 电力系统自动化, 2021, 45(1): 28-35.

FAN Hang, ZHANG Xuemin, MEI Shengwei, et al. Ultra-short-term wind speed prediction model for wind farms based on spatiotemporal neural network[J]. Automation of Electric Power Systems, 2021, 45(1): 28-35.

[11] 李德顺, 李宁, 李银然, 等. 基于小波分解的DIF- RBFNN超短期风速组合预测方法[J]. 兰州理工大学学报, 2019, 45(4): 63-66.

LI Deshun, LI Ning, LI Yinran, et al. Ultra short-term combined forecasting method of wind speed based on DIF-RBFNN with wavelet decomposition[J]. Journal of Lanzhou University of Technology, 2019, 45(4): 63-66.

[12] 张亚刚, 赵媛, 王增平. 基于Lorenz扰动分布和VMD的神经网络风速预测研究[J]. 华北电力大学学报(自然科学版), 2019, 46(4): 8-15.

ZHANG Yagang, ZHAO Yuan, WANG Zengping. Wind speed prediction based on Lorenz disturbance distribution and variational mode decomposition[J]. Journal of North China Electric Power University (Natural Science Edition), 2019, 46(4): 8-15.

[13]DING Wen, MENG Fanyong. Point and interval forecasting for wind speed based on linear component extraction[J]. Applied Soft Computing Journal, 2020, 93.

[14] ZHANGYagang, PAN Guifang, ZHAO Yunpeng, et al. Short-term wind speed interval prediction based on artificial intelligence methods and error probability distribution[J]. Energy Conversion and Management, 2020, 224.

[15] 沈堉, 魏海坤. 基于RBF神经网络的风电场风速区间预测[J]. 工业控制计算机, 2016, 29(5): 55-57.

SHEN Yu, WEI Haikun. Interval prediction of wind speed based on RBF neural network[J]. Industrial Control Computer, 2016, 29(5): 55-57.

[16] LI Ranran, JIN Yu. A wind speed interval prediction system based on multi-objective optimization for machine learning method[J]. Applied Energy, 2018, 228.

[17] GAN Zhenhao, LI Chaoshun, ZHOU Jianzhong, et al. Temporal convolutional networks interval prediction model for wind speed forecasting[J]. Electric Power Systems Research, 2021, 191.

[18] 陈伟, 郭建鹏, 裴喜平, 等. 风电场短期风速变化区间与变化趋势预测算法[J]. 电力系统及其自动化学报, 2015, 27(9): 47-52.

CHEN Wei, GUO Jianpeng, PEI Xiping, et al. prediction algorithm of change interval and change trend of short-term wind speed in wind farm[J]. Proceedings of the CSU-EPSA, 2015, 27(9): 47-52.

[19]黄文聪, 张宇, 杨远程, 等. 模糊信息粒化和GWO-SVM算法结合的短期风速范围预测[J]. 华侨大学学报(自然科学版), 2020, 41(5): 674-682.

HUANG Wencong, ZHANG Yu, YANG Yuancheng, et al. Short term wind speed range prediction based on fuzzy information granulation and GWO-SVM algorithm[J]. Journal of Huaqiao University (Natural Science), 2020, 41(5): 674-682.

[20]殷豪, 黄圣权, 刘哲, 等. 基于模糊信息粒化和长短期记忆网络的短期风速预测[J]. 电测与仪表, 2019, 56(11): 101-107.

YIN Hao, HUANG Shengquan, LIU Zhe, et al. Short-term wind speed prediction based on fuzzy information granulation and LSTM[J]. Electrical Measurement & Instrumentation, 2019, 56(11): 101-107.

[21] 曾云, 殷豪, 刘哲. 基于EWT-FIG和ORELM模型的风速多步区间预测[J]. 宁夏电力, 2018(4): 6-13.

ZENG Yun, YIN Hao, LIU Zhe. Wind speed multi-step interval prediction based on EWT-FIG and ORELM model[J]. Ningxia Electric Power, 2018(4): 6-13.

[22] 范磊, 卫志农, 李慧杰, 等. 基于变分模态分解和蝙蝠算法-相关向量机的短期风速区间预测[J]. 电力自动化设备, 2017, 37(1): 93-100.

FAN Lei, WEI Zhinong, LI Huijie, et al. Short-term wind speed interval prediction based on VMD and BA-RVM algorithm[J]. Electric Power Automation Equipment, 2017, 37(1): 93-100.

[23] 赵辉, 周杰, 王红君, 等. 风电场短期风速区间预测[J]. 中国科技论文, 2018, 13(23): 2728-2734.

ZHAO Hui, ZHOU Jie, WANG Hongjun, et al. Short-term wind speed interval prediction based on LMD-FE and HGWO-ELM[J]. China Sciencepaper, 2018, 13(23): 2728-2734.

[24] 白培林, 王皓怀, 李雷, 等. 基于FEEMD-MFO-GPR阳江海上风电场短期风速区间预测[C] // 2019智能电网新技术发展与应用研讨会论文集, 2019: 1-6.

BAI Peilin, WANG Haohuai, LI Lei, et al. Short term wind speed range prediction of Yangjiang offshore wind farm based on FEEMD-MFO-GPR[C] // Proceedings of 2019 Symposium on New Technology Development and Application of Smart Grid, 2019: 1-6.

[25] NAIKJ, BISOI R, DASH P K. Prediction interval forecasting of wind speed and wind power using modes decomposition based low rank multi-kernel ridge regression[J]. Renewable Energy, 2018, 129.

[26] TORRES M E, COLOMINAS M A, SCHLOTTHAUER G, et al. A complete ensemble empirical mode decomposition with adaptive noise[C] // IEEE International Conference on Acoustics, Speech, and Signal Processing, 2011: 4144-4147.

[27] 韩宏志, 唐振浩. 基于CEEMDAN与回声状态网络的风速预测方法[J]. 电力系统保护与控制, 2020, 48(12): 90-96.

HAN Hongzhi, TANG Zhenhao. Wind speed prediction method based on CEEMDAN and echo state network[J]. Power System Protection and Control, 2020, 48(12): 90-96.

[28] 熊景华, 茹璟. 基于随机森林算法和模糊信息粒化的汇率预测组合模型研究[J]. 数量经济技术经济研究, 2021, 38(1): 135-156.

XIONG Jinghua, RU Jing. Research on exchange rate forecasting integrated model based on random forest and fuzzy information granulation[J]. The Journal of Quantitative & Technical Economics, 2021, 38(1): 135-156.

[29] 王凌云, 林跃涵, 童华敏, 等. 基于改进Apriori关联分析及MFOLSTM算法的短期负荷预测[J]. 电力系统保护与控制, 2021, 49(20): 74-81.

WANG Lingyun, LIN Yuehan, TONG Huamin, et al. Short-term load forecasting based on improved Apriori correlation analysis and MFOLSTM algorithm[J]. Power System Protection and Control, 2021, 49(20): 74-81.

[30] 史加荣, 赵丹梦, 王琳华, 等. 基于RR-VMD-LSTM的短期风电功率预测[J]. 电力系统保护与控制, 2021,49(21): 63-70.

SHI Jiarong, ZHAO Danmeng, WANG Linhua, et al. Short-term wind power prediction based on RR-VMD- LSTM[J]. Power System Protection and Control, 2021, 49(21): 63-70.

Ultra short term wind speed interval prediction based on a hybrid model

ZHANG Jinliang, LIU Ziyi

(School of Economics and Management, North China Electric Power University, Beijing 102206, China)

Accurate wind speed prediction can promote large-scale wind power integration and ensure the safe and stable operation of a power system. There is a problem in that traditional point prediction methods find it difficult to represent the probability credibility of prediction results. This paper proposes a hybrid interval prediction model based on fuzzy information granulation, an improved long short-term memory network and an autoregressive integrated moving average model. First, the original wind speed data is decomposed by a complete set empirical mode decomposition model of adaptive noise, and the new sequence is reconstructed according to fuzzy entropy. Then the fuzzy information of each sequence is granulated to obtain the maximum, minimum and average values. Finally, the improved long short-term memory network model is used to predict the high-frequency series, and the autoregressive integrated moving average model is used to predict the low-frequency series and the remainder, and then the obtained upper and lower bounds are summed to obtain the final wind speed interval. Example analysis shows that the wind speed prediction interval obtained by this model can accurately cover the measured wind speed and provide more valuable decision-making information for power system dispatching.

wind speed interval prediction; fuzzy information granulation; improved long short-term memory neural network; ARIMA model; hybrid model

10.19783/j.cnki.pspc.220241

国家自然科学基金项目资助(71774054)；中央高校基本科研业务专项资金资助(2019MS055)

This work is supported by the National Natural Science Foundation of China (No. 71774054).

2022-02-28；

2022-05-23

张金良(1981—)，男，博士，教授，研究方向为能源经济管理；E-mail: zhangjinliang1213@163.com

刘子毅(1996—)，男，硕士研究生，研究方向为能源经济预测。E-mail: lzy2462071583@163.com

(编辑 姜新丽)