提高串联锂电池SOC在线估计快速性的简化二阶模型

任碧莹，孙 佳，孙向东，徐玮浓

提高串联锂电池SOC在线估计快速性的简化二阶模型

任碧莹，孙 佳，孙向东，徐玮浓

(西安理工大学电气工程学院，陕西 西安 710054)

锂离子电池最常用的等效电路模型为二阶RC等效电路模型。基于该模型的参数辨识存在所需辨识参数多、运算量大的缺点，同时荷电状态(state of charge, SOC)估计中状态方程存在复杂的指数运算等问题，这些都使得难以对多个串联电池进行SOC的在线估计。因此，提出了一种简化二阶电池模型。该模型忽略电池内部极化反应，只关注其外特性，使得参数辨识个数减少。该简化模型也使得状态空间方程中需要估计的状态变量个数减少，避免了复杂的指数运算，降低了计算复杂度和整体的运算量，有利于多个串联锂电池SOC的实时在线估计。通过对单体锂电池和串联锂电池进行参数辨识和SOC估计测试，验证了所提的简化模型在保证参数辨识及SOC估计精度的同时，大大提升了系统运算速度，进而提高了SOC估计的快速性。

锂离子电池；简化二阶模型；参数辨识；SOC估计

0 引言

近年来新能源产业的发展为解决传统化石能源危机提供了可行之道[1]，新能源汽车则是其中的代表之一[2]。锂电池因其循环寿命长、能量密度高、自放电率低、安全可靠等优点在电动汽车和交直流微电网等领域得到广泛应用。荷电状态(SOC)作为电池管理系统的关键[3-8]，进行快速而又高精度的SOC在线估计既有利于防止锂电池发生过充过放等不安全事故，也有利于延长锂电池的使用寿命[9]，同时也为串联锂电池SOC均衡控制提供了准确的依据[10]。

锂电池的等效电路模型能够较好的描述电池的性能，适合应用于实际工程实践中。SOC在线估计的准确性和快速性取决于锂电池等效电路模型本身的精度和复杂度；同时以高精度的参数辨识为基础，才能获得高精度的SOC估计。锂电池等效电路模型主要包括内阻模型、阻容模型、PNGV模型、GNL模型、戴维南模型[11-12]。其中，内阻模型结构较为简单，但该模型不能很好地模拟电池在各种工况下的动态特性，实际中应用精度低。阻容模型能够将电池特性较好地体现出来，但电容电压难以测量。PNGV模型实用性较低。GNL模型虽然有着较高的精度，但所需辨识的参数较多，增大了计算复杂度。而戴维南模型可以通过改变RC阶数的个数调节模型的精度与复杂度，综合考虑模型精度和复杂度[13]，本文以二阶RC模型为基础来进行分析。

针对二阶RC模型，为了得到高精度的模型参数进而得到比较准确的SOC估计值，研究者们对参数辨识算法与SOC估计算法的设计越来越完善，但同时也使得算法的计算复杂度越来越高。例如，目前参数辨识的方法有极大似然法、随机梯度法、递推最小二乘法(RLS)、含遗忘因子最小二乘法(FFRLS)、变遗忘因子最小二乘法(VFFRLS)等[14-16]。而常用的SOC估计方法有开环估计算法和基于模型的闭环估计算法。开环估计算法包括安时积分法、开路电压法、负载电压法[17-18]。开环估计算法原理简单、容易实现且计算复杂度低，但大多需要满足许多前提条件，且因为缺少反馈环节，算法鲁棒性较差。而基于模型的闭环估计算法不需要精确的SOC初值，比如，卡尔曼滤波法(KF)、扩展卡尔曼滤波法(EKF)、无迹卡尔曼滤波法(UKF)、自适应卡尔曼滤波(AKF)[19-21]等。KF是一种时域上的最优滤波算法，它是以最小均方差为最佳准则，通过线性系统状态方程以及系统输入输出观测数据，对系统状态进行最优估计。然而，由于电池是一个复杂的非线性系统，因此目前常用于电池SOC估计的是一些非线性卡尔曼滤波算法，如：EKF、UKF、AKF等。这些闭环算法使得SOC估计精度越来越高，但同时也增大了计算复杂度，快速性无法保证。

无论是基于等效电路模型的参数辨识方法还是SOC估计方法，在保证精度的前提下，要提高参数辨识速度或SOC估计速度，都和模型中需要辨识的参数个数和计算的复杂度直接相关。现有的二阶RC等效电路模型参数个数多，且进行SOC估计时需要指数计算，导致在线参数辨识和在线SOC估计的实时性较差。非线性滤波器和高阶电池模型的复杂计算使得在串联锂电池应用场合中，多个电池单体的SOC在线实时估计难以保证。

因此，希望设计简化电路模型，减少辨识参数的个数，以及采用线性化的SOC估计方法，使得系统在保证SOC估计精度的同时极大的提高运算速度。本文针对电池稳定运行时的特性，简化传统二阶RC等效电路模型，得到简化后参数辨识的数学表达式，并对电池模型输出方程进行线性化处理得到呈现线性特性的状态方程，进而使用简单的RLS和KF算法相结合进行SOC估计，可以使得系统的运算量大大地减少，进而提高系统的实时性。

本文首先在第1节阐述了常规的二阶RC电路模型和以该模型为基础的SOC估计状态空间方程。经研究在锂电池稳定状态时状态方程矩阵系数基本稳定，基于此在第2节提出了简化的二阶模型，基于该模型需要辨识的参数个数有所减少，同时使得SOC估计运算简单，从整体上减小了系统的运算量和运算复杂度，为串联锂电池在线SOC估计奠定基础。在第3节针对单体锂电池进行参数辨识和SOC估计，对比了二阶RC模型和简化二阶模型下的SOC估计运行时间和精度；在此基础上进行了多个串联锂电池的在线SOC估计。

1 锂电池二阶RC等效电路模型

1.1 基于二阶RC等效电路模型的状态空间方程

锂电池二阶RC等效电路模型如图1所示，模型中参数包括电池内阻，极化电阻，极化电容，两个并联RC分别表示了电池的电化学极化过程与浓差极化过程，分别表示两个并联RC支路的极化电压，表示开路电压，表示端电压，表示端电流。

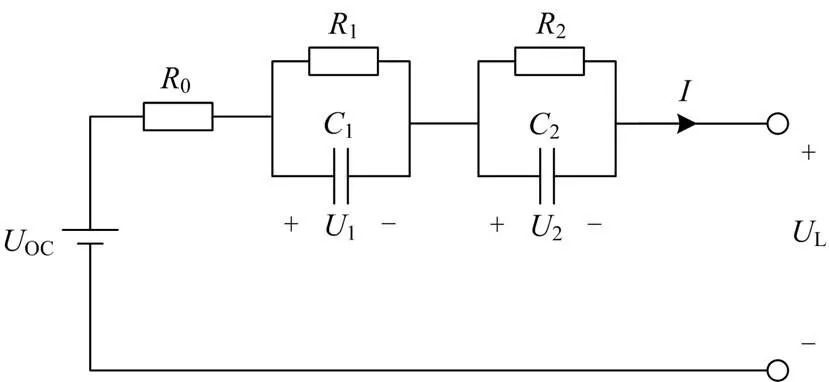
图1 锂电池二阶RC等效电路模型

由图1根据基尔霍夫定律可得

安时积分法计算SOC的公式如式(2)所示。

(2)

在考虑噪声的情况下对式(3)进行离散化处理，得到用于SOC估计的离散化状态空间方程如式(4)所示(包括状态方程和输出方程)[22]。

式中：系统输入()=()，系统输出；矩阵；，为采样时间；()为过程噪声，服从正态分布；()是观测噪声，服从正态分布；其中和分别为过程噪声和观测噪声的协方差。

1.2 基于二阶RC等效电路模型的参数辨识表达式

对二阶RC等效电路模型的时域关系进行拉普拉斯变换并整理可得参数与观测值的关系如式(5)所示。

将式(6)写作如式(7)所示形式。

2 简化二阶模型

2.1 简化二阶模型

根据第1节对参数辨识的分析可以看出，算法计算量最大最复杂的地方在于对电池模型中RC参数的辨识，RC参数在每个采样点处的辨识结果用于SOC估计时对状态空间方程式(4)中矩阵、以及0的实时更新，从而利用SOC估计算法达到对所估状态变量的实时更新。

图2 状态方程中各系数变化曲线

图3 简化二阶模型

图3中将RC并联支路看作一个整体，只看其电压1、2的变化情况，本文将在该简化二阶模型的基础上进行分析。

2.2 基于简化二阶模型的锂电池参数辨识

由图3可得系统的输出方程如式(8)所示。

式(8)中令

常规的二阶RC模型需要辨识5个参数：0、1、2、1、2，其计算过程相当复杂，而本节所提出的简化二阶模型只需要辨识3个参数：0、1、2，并且计算简单，大大降低了辨识运算的复杂度和计算量。

本文将采用比较简单的RLS算法进行参数辨识，该算法的递推过程如下。

(1) 初始化协方差矩阵和待估参数向量；

(2) 计算增益向量；

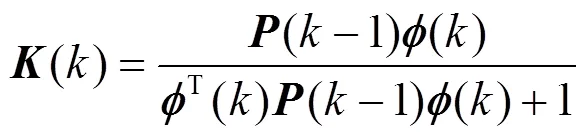
(4) 更新协方差矩阵。

循环步骤(2)—(4)直至采样结束。

2.3 基于简化二阶模型的线性化的SOC估计

不难看出式(13)为线性方程，但系统输出方程式(8)由于OC和SOC的非线性关系而呈现非线性，若将OC-SOC关系曲线线性化，那么就可以使用简单的KF算法进行SOC估计。

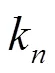
至此，可将状态空间方程式(4)简写为如式(16)形式。

利用KF进行SOC估计的过程如下。

步骤1：初始化状态变量、协方差矩阵、过程噪声协方差和观测噪声协方差。

步骤2：状态预测。

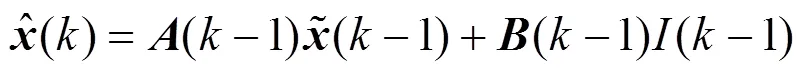
步骤3：协方差预测。

步骤4：卡尔曼增益的求取。

步骤5：状态更新。

步骤6：协方差更新。

基于传统二阶RC等效电路模型的SOC估计是在状态空间方程式(4)的基础上通过复杂的指数运算不断更新矩阵、进而利用估计算法实时更新状态向量() = [()1()2()]T的最优估计值，一系列繁琐的计算不但会造成一定的误差，同时还会使整体算法的计算时长大大增加。而基于简化模型的SOC估计，由于状态变量1和2在前述参数辨识中已经得到，所以在步骤2和步骤5中仅基于状态空间方程式(16)对状态变量SOC进行预测和更新，并且在整体的计算过程中省去了复杂矩阵的更新，从而使得整体计算大大简化。

本文利用RLS参数辨识算法以及线性KF算法对电池进行SOC联合估计的具体流程如图4所示。

图 4 基于简化二阶模型的SOC联合估计流程图

由2.2节和2.3节可以明显看出，和传统二阶RC模型相比，所提简化模型不论是在参数辨识还是在SOC估计上其推导和计算过程的复杂度都大幅降低。其中，在参数辨识中舍弃了传统二阶RC模型通过复杂推导得到的参数辨识数学表达式式(6)，而采用式(9)进行参数辨识，减少了参数辨识个数并使得计算量大大下降；在SOC估计部分，将状态空间方程式(4)简化为式(16)，减少了需要估计的状态变量，并且使得状态空间方程整体线性化，适合采用线性KF算法进行SOC估计。整体来讲，基于所提简化二阶模型进行参数辨识和SOC联合估计将会使得单体在线SOC估计的效率大大提升，从而能够保证多个串联单体同时进行SOC估计的实时性。

3 单体锂电池和串联锂电池在线SOC估计验证

锂电池测试平台如图5所示。锂电池经电压电流探头接于电池测试柜，电池测试仪获取电池数据，将其与上位机连接构成测试平台，上位机、中位机与电池测试柜之间通过通信线相连，用于传输数据与控制信号。

图5 锂电池测试平台

本文所用锂电池单体参数如表1所示，采用0.33C标准速率电流对单个锂电池进行DST充放电工况下的实验测试，在此基础上进行所提简化模型的参数辨识和SOC估计。本节将从均方根误差(RMSE)、平均相对误差(MRE)以及运行时间3个方面对不同模型下的参数辨识以及SOC估计性能进行对比分析，其中RMSE和MRE的计算公式如式(22)所示。

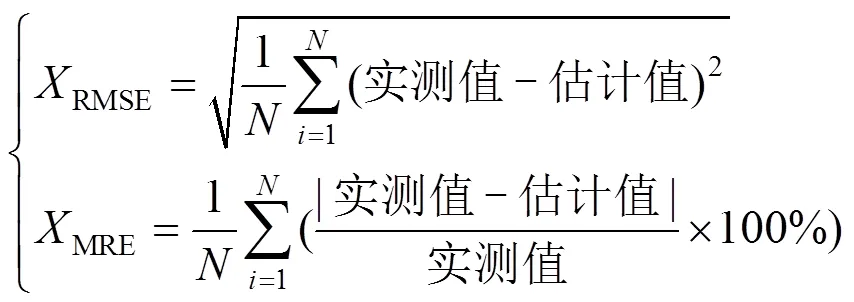
表1 锂电池参数

图6为采用RLS辨识方法对简化二阶模型中0、1、23个参数的辨识结果。

图7为不同模型在RLS算法下辨识的锂电池端电压与实测端电压对比图。根据图7可以获得基于两种模型进行参数辨识的性能对比，如表2所示。

图7 基于两种模型的参数辨识结果对比

表2 两种模型应用于参数辨识时的性能对比

由表2可以看出，基于简化二阶模型的辨识结果与二阶RC模型相比，MRE有一定的降低而RMSE略有升高，即简化二阶模型下参数辨识的整体误差有所下降，但局部存在误差升高的现象，结合图7可以看出，简化模型对于电池极化特性的跟踪性能低于二阶RC模型，但整体应用效果良好，且算法运算时间大大降低。总的来说，两种模型在参数辨识误差相差不大的情况下，所提简化模型从很大程度上提升了算法的实时性，具有更好的整体性能。

图8为基于简化二阶模型和二阶RC模型的SOC估计结果对比。可以看出，基于简化二阶模型对单体电池进行SOC联合估计可以得到较为准确的SOC估计值。

表3为基于两种模型进行SOC联合估计的性能分析。可以看出，基于简化二阶模型的SOC估计误差相比于二阶RC模型没有明显区别，但简化模型的运行时间更短，有着更快的SOC估计速度，大大提升了算法的整体性能。

图8 基于两种模型的SOC估计结果对比

表3 两种模型应用于SOC联合估计时的性能对比

经过上述电池单体参数辨识和SOC估计验证，可以看出基于简化二阶模型的SOC估计精度满足需求，且运算时间大大减少。在此基础上，将简化二阶模型应用到4个初始SOC不同的串联锂电池组中。

图9为4个串联锂电池组各电池初始SOC分别为0.8、0.7、0.65和0.9 时，各锂电池SOC联合估计的结果。可以看出，将简化二阶模型应用于串联电池组中对各单体进行SOC估计时，各电池单体均能得到较为精确的估计结果，估计值与真实值重合度较高。图10为SOC估计误差曲线图，可以看出，各单体估计误差非常小，都能保持在0.035%以下，仍能够保证SOC估计误差在需求范围内。

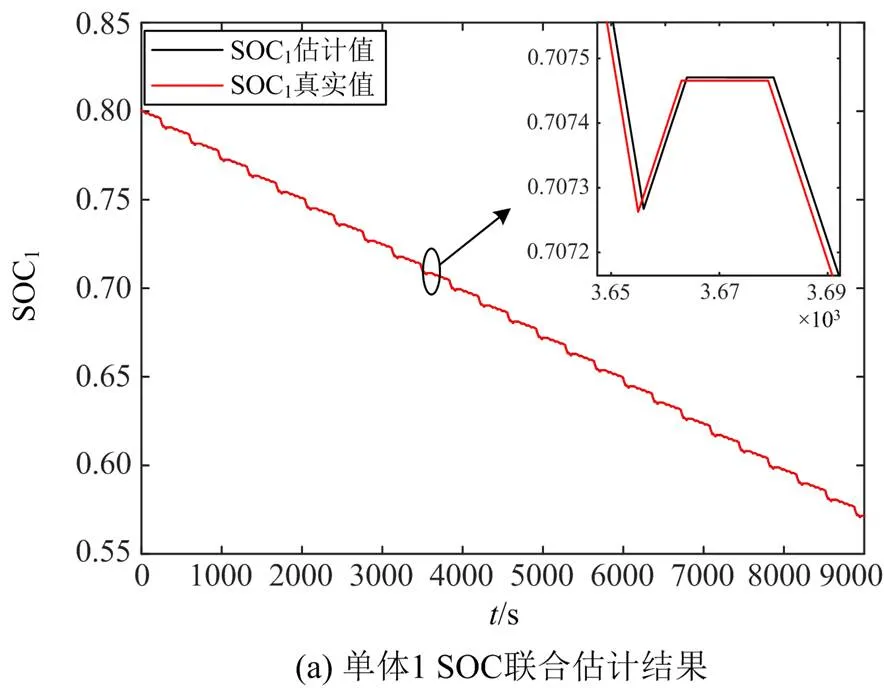
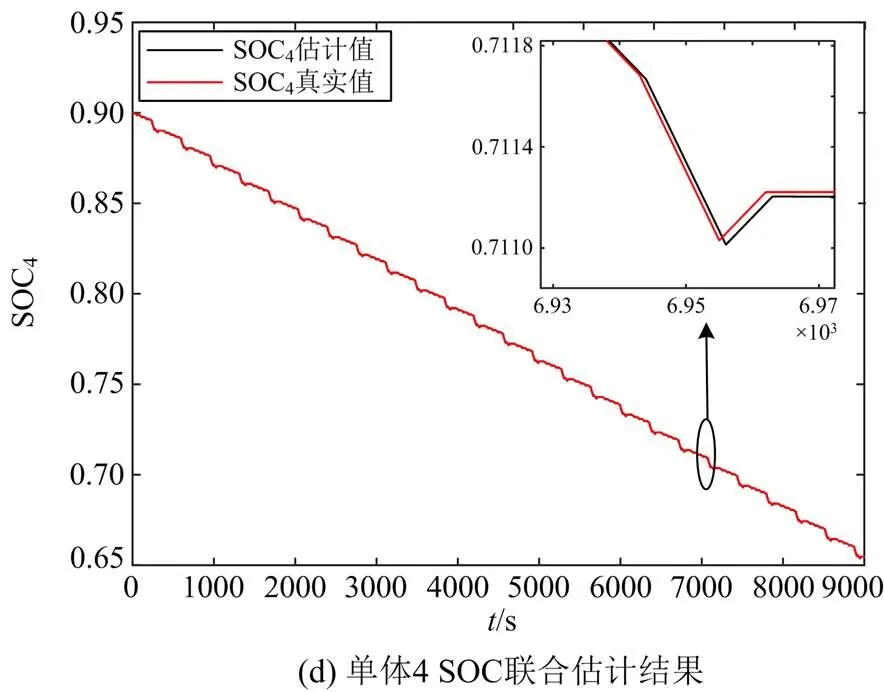
图9 串联电池组中各电池单体SOC联合估计结果

图10 串联电池组中各电池单体SOC联合估计误差

4 结论

本文针对以二阶RC电路模型为基础进行参数辨识与SOC估计时由于算法复杂度较高，导致实际应用中实时性差的问题，提出了简化二阶模型，该模型减少了需要辨识的参数个数，并且在此基础上简化了用于SOC估计的状态方程，避免了SOC估计过程中复杂矩阵的更新，大大降低了整体算法的复杂度以及运算量，在提高参数辨识速度的基础上同时也进一步提高了SOC估计的效率。实验结果表明，和传统模型相比，所提模型在满足精度的要求下，大幅提升了SOC估计效率，验证了所提模型的可行性。

未来一方面可以根据电池老化的速度在本文所提模型的基础上考虑参数更新的频率，以满足电池在不同老化阶段下模型的精度；另一方面在权衡模型复杂度的基础上，可进一步研究混合建模的方法以弥补单一建模的缺点；此外还应考虑温度等因素对电池特性的影响，进一步提高电池模型精度。

[1] 李秋燕, 王利利, 张艺涵, 等. 能源互联网多能流的耦合模型及动态优化方法综述[J]. 电力系统保护与控制, 2020, 48 (19): 179-186.

LI Qiuyan, WANG Lili, ZHANG Yihan, et al. A review of coupling models and dynamic optimization methods for energy internet multi-energy flow[J]. Power System Protection and Control, 2020, 48(19): 179-186.

[2] 李建林, 李雅欣, 周喜超, 等. 储能商业化应用政策解析[J]. 电力系统保护与控制, 2020, 48(19): 168-178.

LI Jianlin, LI Yaxin, ZHOU Xichao, et al. Analysis of energy storage policy in commercial application[J]. Power System Protection and Control, 2020, 48(19): 168-178.

[3] 明彤彤, 赵晶, 王晓磊, 等. 基于改进LSTM的脉冲大倍率工况下锂电池SOC估计[J]. 电力系统保护与控制, 2021, 49(8): 144-150.

MING Tongtong, ZHAO Jing, WANG Xiaolei, et al. SOC estimation of a lithium battery under high pulse rate condition based on improved LSTM[J]. Power System Protection and Control, 2021, 49(8): 144-150.

[4] LÜ J C, JIANG B C, WANG X L, et al. Estimation of the state of charge of lithium batteries based on adaptive unscented Kalman filter algorithm[J]. Electronics, 2020, 9(9): 1425-1425.

[5] 高金辉, 朱迎正. 基于新电源模型的动力锂电池荷电状态估计研究[J]. 河南师范大学学报(自然科学版), 2019, 47(1): 58-61, 92.

GAO Jinhui, ZHU Yingzheng. Study on state estimation of power lithium battery based on new power supply model[J]. Journal of Henan Normal University (Natural Science Edition), 2019, 47(1): 58-61, 92.

[6] 唐传雨, 韩华春, 史明明, 等. 基于DEKF的储能电池系统SOC估计方法研究[J]. 电力工程技术, 2021, 40(3): 7-14.

TANG Chuanyu, HAN Huachun, SHI Mingming, et al. SOC estimation method of battery energy storage system for BMS test platform[J]. Electric Power Engineering Technology, 2021, 40(3): 7-14.

[7] 张小辉, 许傲然, 王秀平. 回溯搜索算法改进RBF算法的锂离子电池SOC估算研究[J]. 电测与仪表, 2020, 57(18): 146-152.

ZHANG Xiaohui, XU Aoran, WANG Xiuping. Research on lithium-ion battery SOC estimation based on backtracking search algorithm and improved RBF algorithm[J]. Electrical Measurement & Instrumentation, 2020, 57(18): 146-152.

[8] 刘运鑫, 姚良忠, 周金辉, 等. 基于LSTM的锂电池储能装置SOC与SOH联合预测[J]. 全球能源互联网, 2022, 5(1): 37-45.

LIU Yunxin, YAO Liangzhong, ZHOU Jinhui, et al. Joint Prediction of state of charge and state of health based on LSTM for lithium-ion batteries[J]. Journal of Global Energy Interconnection, 2022, 5(1): 37-45.

[9] DUAN J D, WANG P, MA W T, et al. State of charge estimation of lithium battery based on improved correntropy extended Kalman filter[J]. Energies, 2020, 13(16): 4197-4197.

[10] 程俊, 曲妍, 李媛, 等. 基于剩余电量估计的电池组充放电均衡策略[J]. 电力系统保护与控制, 2020, 48(3): 122-129.

CHENG Jun, QU Yan, LI Yuan, et al. Charge and discharge equalization strategy for battery packs based on remaining capacity estimation[J]. Power System Protection and Control, 2020, 48(3): 122-129.

[11] BACCOUCHE I, JEMMALI S, MANAI B, et al. Li-ion battery modeling and characterization: an experimental overview on NMC battery[J]. International Journal of Energy Research, 2022, 46(4): 3843-3859.

[12] 郭向伟, 司阳, 高岩, 等. 动力锂电池最优等效电路模型研究[J]. 电子测量与仪器学报, 2021, 35(1): 48-55.

GUO Xiangwei, SI Yang, GAO Yan, et al. Research on the optimal equivalent circuit model of lithium-ion battery[J]. Journal of Electronic Measurement and Instrumentation, 2021, 35(1): 48-55.

[13] LI J, WANG L, LÜ C, et al. Parameter updating method of a simplified first principles-thermal coupling model for lithium-ion batteries[J]. Applied Energy, 2019, 256(1): 1-15.

[14] SUN X D, JI J R, REN B Y, et al. Adaptive forgetting factor recursive least square algorithm for online identification of equivalent circuit model parameters of a lithium-ion battery[J]. Energies, 2019, 12(12): 2242-2242.

[15] SONG Q, MI Y, LAI W. A novel variable forgetting factor recursive least square algorithm to improve the anti-interference ability of battery model parameters identification[J]. IEEE Access, 2019, 7: 61548-61557.

[16] REN B Y, XIE C X, SUN X D, et al. Parameter identification of a lithium-ion battery based on the improved recursive least square algorithm[J]. IET Power Electronics, 2020, 13(12): 2351-2358.

[17] NAGUIB M, KOLLMEVER P, EMADI A. Lithium-ion battery pack robust state of charge estimation, cell inconsistency, and balancing: review[J]. IEEE Access, 2021, 9: 50570-50582.

[18] ZHOU W, ZHENG Y, PAN Z, et al. Review on the battery model and SOC estimation method[J]. Processes, 2021, 9(9): 1685.

[19] VAN C N, VINH T N. SOC estimation of the lithium-ion battery pack using a sigma point Kalman filter based on a cell’s second order dynamic model[J]. Applied Sciences, 2020, 10(5): 1896.

[20] WANG S L, FERNANDEZ C, ZOU C Y, et al. A comprehensive working state monitoring method for power battery packs considering state of balance and aging correction[J]. Energy, 2019, 171(2): 444-455.

[21] ZZA B, LI J A, LZ A, et al. State-of-charge estimation of lithium-ion battery pack by using an adaptive extended Kalman filter for electric vehicles[J]. Journal of Energy Storage, 2021, 37(9): 102457.

[22] LI J H, GAO F J, YAN G G, et al. Modeling and SOC estimation of lithium iron phosphate battery considering capacity loss[J]. Protection and Control of Modern Power Systems, 2018, 3(1): 61-69.

[23] SONG Q, MI Y, LAI W. A novel variable forgetting factor recursive least square algorithm to improve the anti-interference ability of battery model parameters identification[J]. IEEE Access, 2019, 7: 61548-61557.

[24] DU X, MENG J, ZHANG Y, et al. An information appraisal procedure: endows reliable online parameter identification to lithium-ion battery model[J]. IEEE Transactions on Industrial Electronics, 2021, 69(6): 5889-5899.

A simplified second-order model for improving the speed of on-line state of charge estimation of series lithium-ion batteries

REN Biying, SUN Jia, SUN Xiangdong, XU Weinong

(School of Electrical Engineering, Xi’an University of Technology, Xi’an 710054, China)

The most commonly used equivalent circuit model of a lithium-ion battery is the second-order RC equivalent circuit model. Parameter identification based on this model has the disadvantages of many identification parameters and a large amount of calculation. At the same time, there are complex exponential operations in the state of charge (SOC) estimation, and these make it difficult to estimate the SOC of multiple series batteries on-line. Therefore, a simplified second-order battery model is proposed, one which ignores the internal polarization reaction and only pays attention to its external characteristics, so as to reduce the amount of parameter identification. The simplified model also reduces the number of state variables to be estimated in the state space equation, avoids complex exponential operation, reduces the computational complexity and the overall amount of operation, and is conducive to the real-time online estimation of the SOC of multiple series lithium batteries. Through the parameter identification and SOC estimation test of a single lithium-ion battery and series lithium-ion batteries, it is verified that the proposed simplified model not only ensures the accuracy of parameter identification and SOC estimation, but also greatly increases the operational speed of the system, and then improves the speed of SOC estimation.

lithium-ion battery; simplified second-order model; parameter identification; SOC estimation

10.19783/j.cnki.pspc.220174

国家自然科学基金项目资助(51577155)；陕西省自然科学基金项目资助(2020JM-449)

This work is supported by the National Natural Science Foundation of China (No. 51577155).

2022-02-14；

2022-03-23

任碧莹(1971—)，女，博士，教授，研究方向为新能源发电技术与微电网控制技术；E-mail:renby@126.com

孙 佳(1997—)，女，通信作者，硕士研究生，研究方向为电池管理和储能变换器技术。E-mail: 1776107172@ qq.com

(编辑 魏小丽)