变截面箱梁桥悬臂施工过程剪力滞效应

陈建民， 骆维斌*， 冀伟

(1.公路建设与养护技术材料及装配交通运输行业研发中心， 兰州 730030； 2.兰州交通大学土木学院， 兰州 730070)

变截面预应力混凝土连续箱梁桥因其抗弯抗扭刚度大、湿接缝少和外形简洁美观等优点，在现代桥梁建设中得到广泛使用。剪力滞效应是在梁受弯时由于翼缘板的剪切变形不均匀而造成的弯曲正应力沿梁宽方向分布不均匀的现象[1]。国内外学者对剪力滞效应开展了大量的研究，王连广等[2]在研究钢-混凝土组合箱梁剪力滞效应时，利用变分原理推导了典型的简支组合箱梁在跨中集中荷载作用下的解析解；江林松等[3]在对比分析了中外典型规范对钢-混组合连续直梁桥有效宽度计算结果的基础上，基于数值模拟，研究了小半径双工字钢-混组合连续弯梁桥的剪力滞效应和有效宽度，提出有限宽度的简化计算方法；周茂定等[4]对薄壁箱梁的剪力滞翘曲位移函数进行了修正，研究了箱梁高宽比、宽跨比、板宽比等参数对剪力滞的影响；赵志峰等[5]基于比拟杆法，研究了单箱三室薄壁箱梁分别在集中荷载作用和均布荷载作用下的剪力滞效应；Boules[6]通过有限元模拟，研究了U形梁的翘曲变形和剪力滞效应；舒小娟等[7]在综合考虑全截面剪切应变能的基础上，利用能量变分原理建立了剪滞位移的弯曲剪力滞控制微分方程组；朱力等[8]提出了一种考虑滑移时，求解钢-混凝土组合箱型梁剪力滞效应的理论模型；卫星等[9]研究了单箱双室波形钢腹板PC组合梁的剪力滞效应；刘洋等[10]以兰州河口大桥为工程背景，研究了后续施工以及施工工况变化对已完成梁段剪力滞效应影响；王旭飞等[11]利用能量变分原理和有限元，研究了双线混凝土U形梁的剪力滞效应；Kraus[12]研究了梁弯曲应力受剪力滞效应影响程度大小及规律；潘旦光等[13]以等截面Euler梁的自由振动模态为Ritz基函数，研究了变高度箱梁的剪力滞效应；周聪等[14]利用比拟杆法研究了变截面波形钢腹板组合箱梁的剪力滞效应；邓德员等[15]利用比拟杆法对箱形截面的剪力滞效应进行分析，推导承受集中荷载和均布荷载的简支梁考虑剪力滞效应的正应力计算公式。

然而，对连续箱梁悬臂施工阶段剪力滞效应研究较为匮乏，现以某新建(48+80+48) m预应力混凝土连续梁桥为背景，研究变截面预应力混凝土连续箱梁桥在悬臂施工阶段的剪力滞效应及其变化规律。所采用试验研究方法及成果可为同类桥梁的剪力滞分析提供参考。

1 剪力滞效应理论

初等梁理论中的平截面假定，是指在对称荷载作用下，假定箱梁具有无限抗剪刚度，从而沿梁宽方向产生的弯曲正应力是均匀分布的。而实际的箱梁在荷载作用下产生的弯曲横向力是通过腹板传给翼板，由于剪应力在翼板上的分布是不均匀的，因此剪切变形沿翼板分布也是不均匀的，就引起了翼板的纵向位移随远离腹板距离的增大而滞后，最后造成弯曲正应力在横向分布呈不均匀分布，这种现象称之为剪力滞后效应。剪力滞根据其规律有正剪力滞和负剪力滞之分，其定义为：腹板与翼板交界处的正应力大于按初等梁弯曲理论计算得到的应力值时为正，反之为负[16]，应力分布如图1所示。

图1 箱梁剪力滞效应Fig.1 Shear lag effect of box girder

1.1 剪力滞控制微分方程及边界条件

对于变截面箱梁剪力滞的求解，文献[17]中得到的剪力滞基本微分方程为

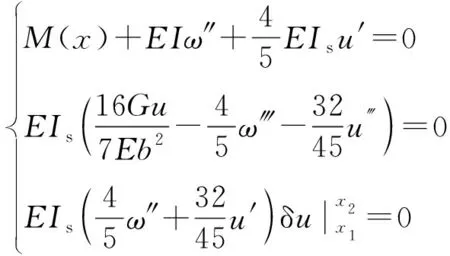
(1)

式(1)中:M(x)为梁体弯矩；E为混凝土弹性模量；I为箱梁截面惯性矩；ω为梁体竖向挠度；u为梁体纵向位移；G混凝土剪切模量；Is为翼板惯性矩；b为翼板宽度一半。

在求解变截面箱梁剪力滞时，其截面惯性矩为x的函数，此时箱梁惯性矩和翼板惯性矩可表示为I(x)和Is(x)，将式(1)经过整理，可以得到变截面箱梁剪力滞的微分方程为

(2)

在变截面箱梁中，α(x)沿梁纵向的变化小，因此α(x)的一阶导数几乎为零，进一步造成参数m的值特别小，一般可忽略不计，此时变截面箱梁剪力滞的控制微分方程为

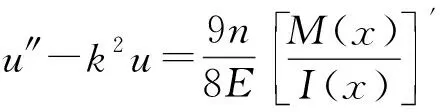
(3)

可进一步求得变截面箱梁翼板位置的剪力滞方程。

翼板和腹板交界位置的剪力滞方程为

(4)

翼板中心位置的剪力滞方程为

(5)

式中：σi表示考虑剪滞效应的变截面箱梁翼板与腹板交界位置的纵向正应力；σc表示考虑剪滞效应的变截面箱梁翼板中心位置的纵向正应力；σ表示按初等梁理论求解的箱梁纵向正应力。

1.2 差分法求解剪力滞系数

对于式(3)变截面箱梁剪力滞控制微分方程的求解，鉴于其方程中系数是变化的，可采用差分原理进行近似求解，差分分格如图2所示。

a表示一个步长图2 变截面箱梁差分分格Fig.2 The difference scheme of variable cross-section cantilever girder

取第i点为研究对象，第一阶和第二阶差分方程为

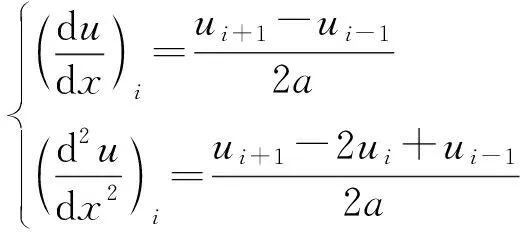
(6)

将式(6)代入式(3)可得变截面箱梁剪力滞控制微分方程的差分表示为

(7)

同理可求得边界条件的差分表示为

(8)

根据悬臂梁边界条件，可以进一步求得施工过程中变截面箱梁剪力滞的求解公式为

(9)

(10)

1.3 求解差分方程

为了保证计算结果的具有相当精度的同时，计算过程又不会很烦琐，因此取4个步距，每个步距长度为a，总共有5个节点(按1～5进行编号)，将每一个节点参数代入到式(7)的差分方程中可得到5个节点差分方程，用矩形的形式表示为

Gu=Q

(11)

式(11)中：G为系数矩阵；u为位移矩阵；Q为荷载矩阵。具体表示为

(12)

G=[u1,u2,…，u5]

(13)

(14)

2 算例分析

2.1 工程概况

以某新建(48+80+48) m预应力混凝土连续梁桥为研究背景，该桥截面采用单箱单室、变截面箱形截面，桥跨布置如图3所示。

图3 连续梁桥跨布置Fig.3 Layout drawing of the continuous girder

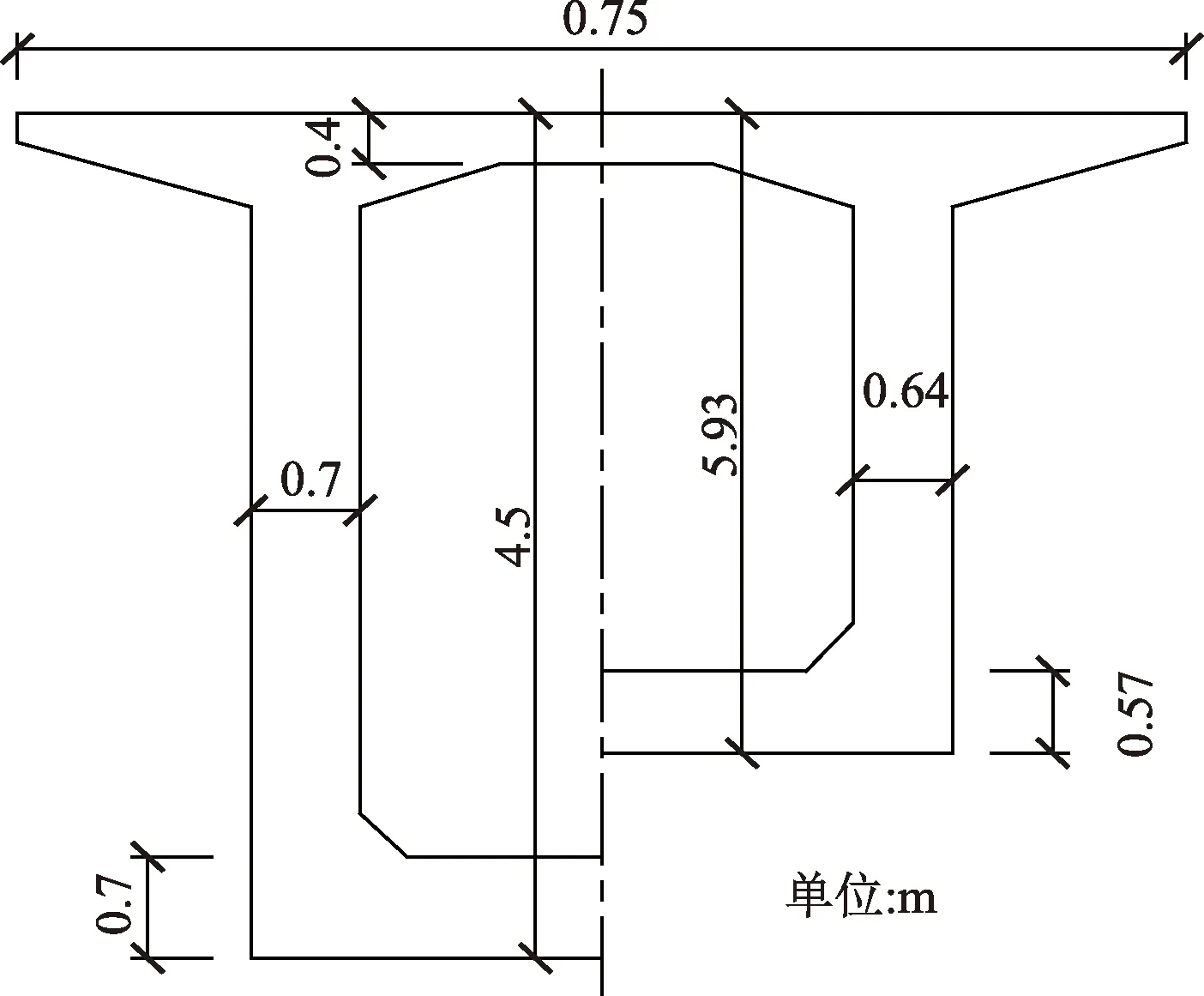
图4 箱梁断面Fig.4 Section diagram of box girder

连续梁挂篮悬臂浇筑施工分为9个梁段，梁段长度布置为(4×3.5+5×4.0) m，现取前4个梁段进行剪力滞系数的研究。1～4号块的梁断面尺寸为：顶板宽7.50 m，顶板厚0.4 m，底板宽4.50 m；梁高、腹板厚和底板厚均按二次抛物线设置成变截面，梁高从5.93 m渐变至4.5 m，底板从0.7 m渐变至0.57 m；腹板由0.7 m渐变至0.6 m，梁横断面如图4所示。

箱梁梁体选用C50混凝土；纵向预应力钢束采用直径为15.2 mm的钢绞线，钢束抗拉强度标准值为1 860 MPa，钢束采用双端张拉；竖向预应力钢筋采用Φ16-2无黏结预应力钢棒。

2.2 变截面箱梁剪力滞求解

从1号梁块到4号梁块合计5个截面，各截面的尺寸以及计算到各截面的惯性矩如表1所示。

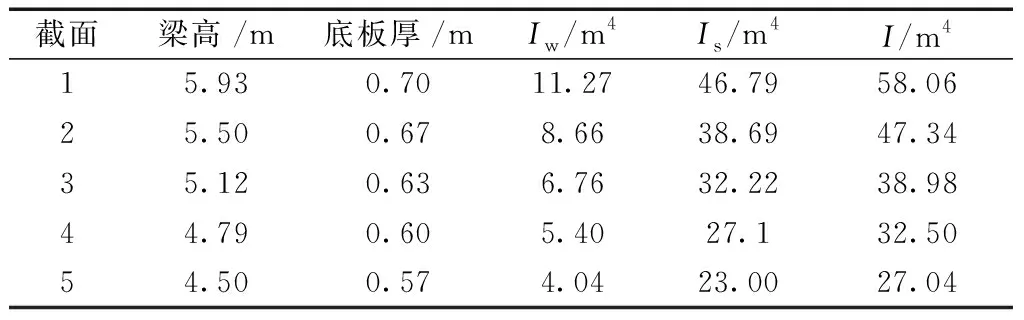
表1 箱梁断面尺寸参数Table 1 Section dimension of the box girder

根据以上理论公式，求得系数矩阵G的各项参数，结果如表2所示。

表2 系数矩阵计算Table 2 Calculation of the coefficient matrix

在求解荷载矩阵Q时，令

(15)

根据理论公式(15)，可以求得荷载矩阵Q的各项参数，如表3所示。将以上数据代入式(9)和式(10)，可以求得翼板和腹板交界位置以及翼板中心位置的剪力滞系数，计算结果如表4所示。

表3 荷载矩阵计算Table 3 Calculation of the load matrix

表4 翼缘板剪力滞计算Table 4 Calculation of the shear lag effect of the flange plate

为了更好地观察变截面箱型悬臂梁的剪力滞变化规律，现将上表计算的剪力滞系数绘于图5中。

由图5可知：变截面箱型连续梁在施工阶段的自重荷载作用下，翼板出现负剪力滞效应。剪力滞效应在固定端最小，随着离固定端距离的增大，剪力滞效应也在逐渐增大。在顶板和腹板交界处的剪力滞系数最小为0.939，在翼板中心处剪力滞系数最大为1.098。

图5 翼缘板剪力滞变化规律Fig.5 Shear lag effect of the flange plate

负剪力滞效应会造成梁体翼板的损坏，甚至造成桥梁倒塌的破坏。为了进一步深入研究变截面箱型梁的剪力滞效应，利用有限元模拟和现场试验的手段，对采用挂篮法施工的变截面箱梁的剪力滞效应做进一步的研究。

3 现场试验

3.1 测点布置

考虑到连续梁的实际情况，在主梁全跨度范围内对称设置7个测试截面，分别是边跨合龙段、零号块、中跨零号块和合龙段，具体截面选择如图6所示。

图6 测试截面选择Fig.6 Selection of the test cross-section

对桥梁结构的实际受力状态进行跟踪监测，不仅可以评价施工的质量，还可以准确地掌握结构的真实应力状态。测试截面一共埋置4个传感器，测点布置如图7所示。

图7 测点布置Fig.7 Layout of measuring points

3.2 传感器布置和数据采集

测试仪器采用振弦式智能温控应力传感器，后端设备采用SS-II频率接收仪和ZHX-1振弦检测仪，根据选定的截面和测点位置，对每一个施工阶段的应力(应变)数据进行采集，如图8所示。

图8 现场传感器布置和数据采集Fig.8 Arrangement of the sensors and the data collection

4 剪力滞效应结果分析

4.1 建立有限元模型

在数值模拟时，采用MIDAS/civil建立梁单元模型，可以有效地计算得到按初等梁理论计算所得的梁截面弯曲应力，全桥总共61个节点，60个梁单元；利用MIDAS/FEA建立实体单元模型，可以有效地得到考虑剪滞效应的弯曲应力，全桥总共8 779个节点，共26 774个实体单元。将最后计算的结果，同现场实验值进行对比分析，有限元模型如图9所示。

图9 变截面箱梁有限元模型Fig.9 Finite element model of variable section box girder

利用有限元模拟，重点对0号块梁端截面和1号块梁端截面的剪力滞进行对比分析，其次是对成桥阶段的全桥沿纵向的剪力滞规律进行分析。

4.2 有限元计算结果分析

施工荷载考虑挂篮自重、现浇混凝土自重和张拉预应力荷载，挂篮悬臂施工的最大悬臂状态是在浇筑9号块时，此时也是最不利荷载工况，此时0号块的纵向正应力如图10所示。

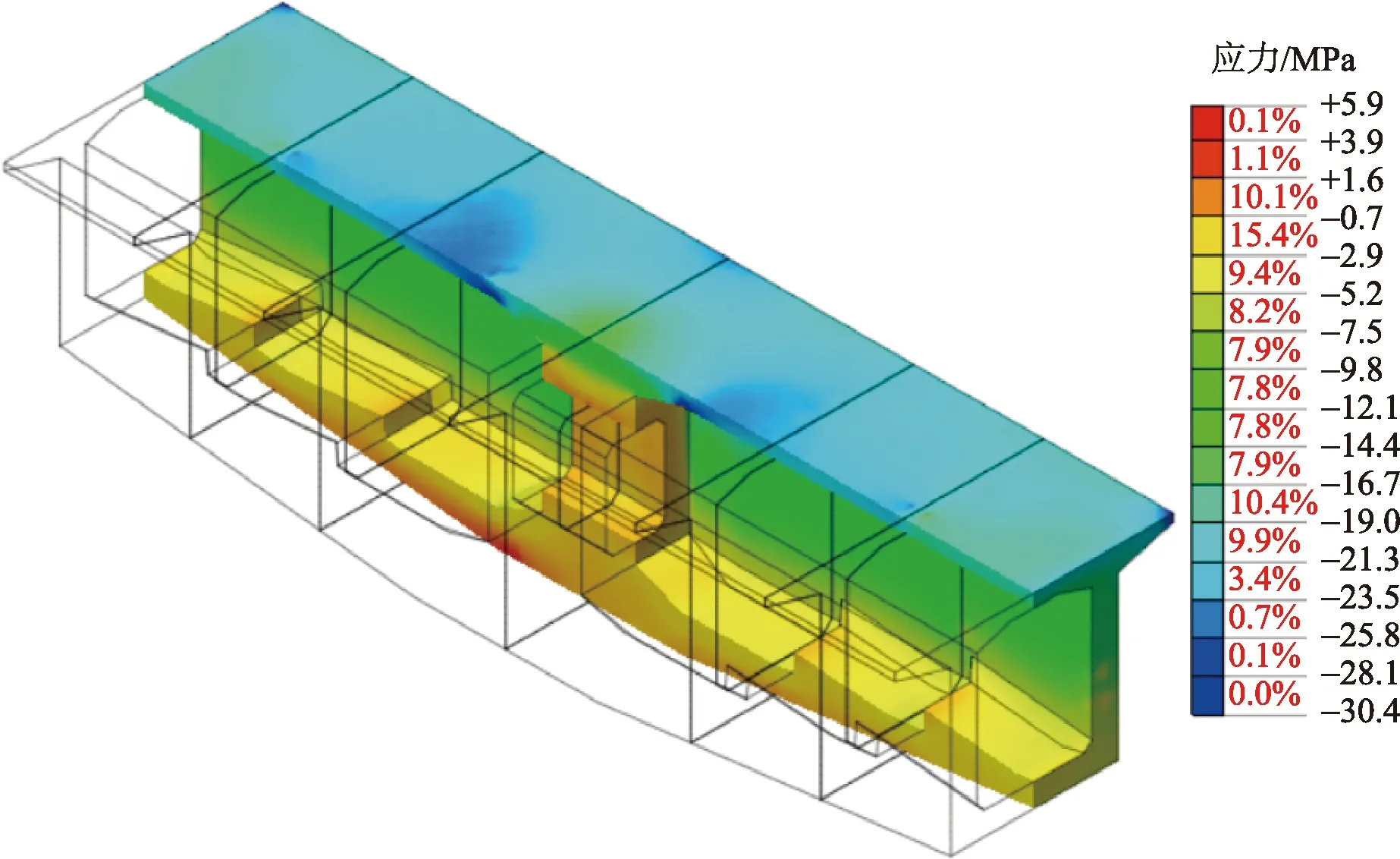
图10 最大悬臂状态时0号块弯曲应力Fig.10 Bending stress of block 0 at maximum cantilever state

利用MIDAS/FEA建立实体单元有限元模型可以有效模拟实际施工中的梁体，从而求得实际的纵向正应力；利用MIDAS/civil建立梁单元有限元模型，求得在初等梁理论假设下的纵向正应力。分别对0号块梁端截面和1号块梁端截面的顶板和底板剪力滞在整个施工过程中的变化规律进行了计算总结，结果如图11和图12所示。

图11 0号梁端截面剪力滞横向变化规律Fig.11 Shear lag effect of the cross section of block-0

图12 1号梁端截面剪力滞横向变化规律Fig.12 Shear lag effect of the cross section of block-1

由图11可以看出，在梁体自重荷载作用下的整个施工阶段，0号梁端截面顶板出现负剪力滞，在9号块钢束张拉后剪力滞效应最明显，最大剪力滞系数为1.06，随着施工的进行，剪力滞效应在不断减小；0号梁端截面底板出现正剪力滞，且在浇筑3号块后剪力滞效应最明显，剪力滞系数最大为1.28，随着施工的进行，剪力滞效应在不断减小，且在合龙后，剪力滞效由正剪力滞变成负剪力滞，此时最大剪力滞系数为1.18。

由图12可以看出，在施工荷载作用下的整个施工阶段，1号梁端截面顶板出现负剪力滞，随着施工的进行，剪力滞效应在不断减小；1号梁端截面底板出现正剪力滞，且在浇筑3号块后剪力滞效应最明显，剪力滞系数最大为1.15，随着施工的进行，剪力滞在不断减小，且在合龙后，剪力滞效由正剪力滞变成负剪力滞，此时最大剪力滞系数为1.13。

4.3 有限元结果和实测值对比分析

根据振弦式智能温控应力传感器测得应变，进一步计算得到实桥应力，再根据剪力滞的定义，求得实际施工中的剪力滞变化规律，再与有限元值进行对比分析，结果如图13和图14所示。

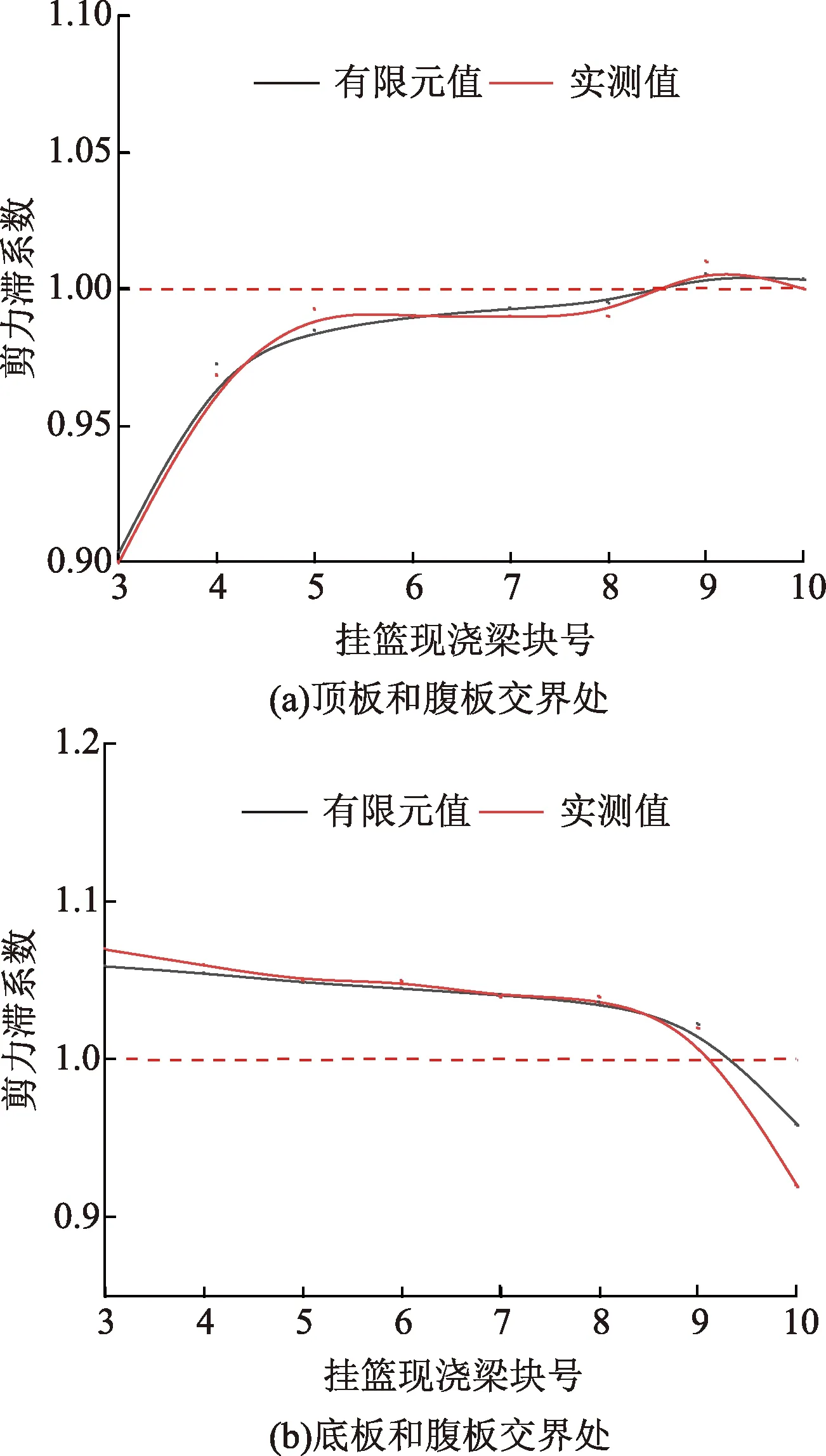
图13 0号梁端截面剪力滞效应Fig.13 Shear lag effect of beam end section of No. 0 beam

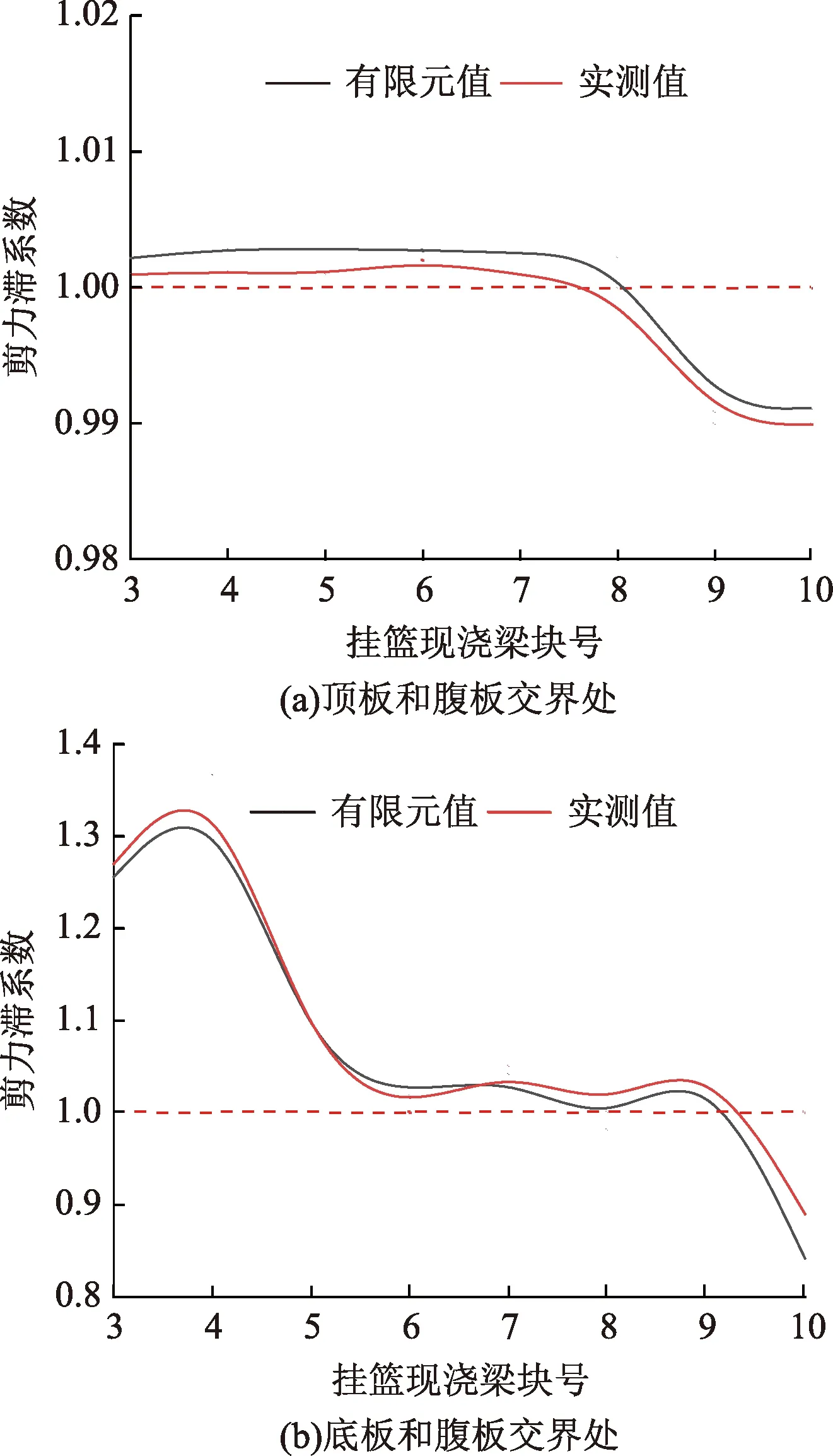
图14 1号梁端截面剪力滞效应Fig.14 Shear lag effect of beam end section of No. 1 beam

由图13可以看出，随着施工的进行，在0号块梁端截面的顶板与腹板交界处出现负剪力滞，剪力滞效应在不断减小；在0号块梁端截面的底板与腹板交界处出现正剪力滞，剪力滞系数在逐渐减小。因此在施工过程中，需重点观察顶板应力，对顶板应力变化实时监控，避免出现应力超限而破坏。

由图14可以看出，随着施工的进行，在1号块梁端截面的顶板与腹板交界处出现正剪力滞，剪力滞效应在不断减小；在0号块梁端截面的底板与腹板交界处出现正剪力滞，剪力滞效应在逐渐减小。其中底板和腹板交界处剪力滞系数最大达到1.34，在施工中应可采取合理配置钢筋和增加角隅等措施来改善此处的受力。

5 结论

以某新建(48+80+48) m变截面箱型预应力混凝土连续梁桥为工程背景，进行其施工阶段剪力滞分析，得到如下结论。

(1) 变截面箱型连续梁在施工阶段的自重荷载作用下，翼板出现负剪力滞效应。剪力滞效应在固定端最小，随着离固定端距离的增大，剪力滞效应也越明显。

(2) 在整个施工阶段，0号块和1号块的顶板均出现负剪力滞效应，随着施工的进行，剪力滞效应在逐渐减小；底板均出现正剪力滞，随着施工的进行，剪力滞效应在逐渐减小。

(3) 在梁体合龙后，0号块和1号块的底板剪力滞效由正剪力滞变成负剪力滞。

(4) 随着施工的进行，0号块梁端顶板和腹板交接处的剪力滞系数在逐渐增大，在底板和腹板交接处剪力滞系数在逐渐减小，1号块梁端截面顶板和腹板交接处、底板和腹板交接处剪力滞系数逐渐减小。