认知超密集网络用户关联与资源分配联合优化遗传算法

张俊杰，仇润鹤*

（1.东华大学 信息科学与技术学院，上海 201620；2.数字化纺织服装技术教育部工程研究中心（东华大学），上海 201620）

0 引言

超密集网络（Ultra-Dense Network，UDN）［1］源自异构网络（Heterogeneous Network），是5G 时代提升系统容量、提高网络覆盖、降低能耗的新型组网技术。认知无线电（Cognitive Radio，CR）［2］用于缓解频谱资源紧张导致的同频干扰问题，由于该技术具备频谱感知与分配的功能，能为非授权用户提供额外的增益良好的授权信道，CR 技术可以成为UDN 中降低干扰、提高频谱利用率的有效技术。已有学者将认知技术与超密集网络结合并展开了研究。

文献［3-4］结合CR 与UDN，提出了在多种场景下的CRUDN 模型，并对比了遗传算法与图着色算法在不同应用场景下资源分配的优劣。文献［5］中提出了在通用衰弱信道下考虑CR-UDN 的干扰分析模型。文献［6-7］中采用分布式算法，利用认知技术将用户分为宏基站（Macrocell Base Station，MBS）服务的宏基站用户和毫微微基站（Femtocell Base Station，FBS）服务的毫微微基站用户；通过FBS 间的磋商进行信道资源的交易，并使用凸近似算法进行功率分配。文献［8-9］中使用拉格朗日对偶方程与卡罗需-库恩-塔克（Karush-Kuhn-Tucker，KKT）条件联合优化了非完美信道、非完美感知下的异构CR-UDN 中的资源分配与功率分配问题。文献［10］中提出了用户基站分布密度均较大时的CR-UDN干扰分析，设计了一种考虑公平性的基于用户分簇的资源分配算法。文献［11］中使用精英保留策略的遗传算法求得次用户最大带宽。

以上文献的研究重点均为资源分配与功率分配问题，随着低功率基站密集化部署，开始出现大量基站覆盖范围的重叠，以用户所在小区划分基站用户的服务关系的方法已不再适用，研究者们开始关注用户关联（User Association，UA）问题，即确定用户与基站间的连接关系。传统网络中一般基于最优参考信号接收功率（Reference Signal Received Power，RSRP）实现UA，但RSRP 使得大量用户倾向接入发射功率更大的MBS，因此不适用于异构网络。在异构超密集网络的研究中，已有研究将UA 问题建模为0/1 背包问题或匹配问题，文献［12］中提出将二部图联合动态规划求解异构网络UA问题，缩小了解的搜索空间，配合拉格朗日对偶方程与KKT条件联合优化资源与功率分配。文献［13］中用MOSEK 求解器和二分类方法解得UA 矩阵，用拉格朗日乘子法解决功率分配问题。文献［14］中基于匹配理论为用户方和基站方各自生成对方的偏好列表，由双方的选择和拒绝操作建立连接关系。文献［15］中提出了一种基于累计分布函数联合优化UA 和资源分配的算法，为同一基站下的不同用户分配时隙资源，最大化系统内用户的长期吞吐量。文献［16］中将UA与资源分配的问题拆分为两个二维匹配问题，采用自适应的遗传算子最大化系统内总吞吐量。

综上文献所述，目前异构网络中的研究多数围绕资源分配与功率分配进行优化，而将UA 作为一个孤立的子问题单独考虑，且多数限于同构网络。同时UA 与资源分配问题间具有较强的耦合性，分步优化会降低算法求解的准确性。目前少有在异构网络中考虑干扰的同时将UA 和资源分配联合优化的研究。因此，对认知超密集网络下的UA 与资源分配的联合优化问题的研究顺应了当前用户基站密集化的发展趋势，具有重要研究意义。从上述文献中还能看出，遗传算法因其不依赖其他先验知识且并行搜索的优势常被用在UA或资源分配这些离散问题的求解中；然而传统遗传算法存在弊端，如对初始种群敏感，迭代出现非法解、收敛慢以及早熟等问题，都会严重影响优化结果。针对上述问题，本文在异构CR-UDN 模型下提出一种改进的遗传算法对UA 和资源分配问题进行联合优化。首先依据基站的覆盖范围和用户类型构建用户可用基站链表和用户可用信道链表；编码阶段采取符号编码，将染色体分为用户-基站部分和用户-信道部分；适应度计算阶段，为降低同频干扰的计算复杂度，以信道为单位计算吞吐量；选择阶段保存动态数量的最优个体，其余部分使用轮盘赌保留，保证遗传算法的种群多样性和收敛性；交叉和变异阶段分别使用多点随机交叉和位移置换算子，并动态变化变异概率，避免早熟而收敛至局部最优。

本文算法的编码方式缩小了最优解的搜索空间，降低了计算复杂度，且使染色体在交叉变异后仍符合约束。遗传算子的设计使得在较少的迭代次数下保证了收敛性，并避免了早熟，有效提高了网络中用户的吞吐量。

1 系统模型与问题描述

1.1 系统模型

本文考虑下行的异构CR-UDN 模型，模型如图1。网络中存在1 个MBS，K个FBS，若干融合中心，M条信道，N个用户。考虑到用户基站间的碰撞体积，将用户分为两部分，第一部分用户按照硬核泊松点过程［17］分布在MBS 的覆盖范围内；第二部分为热点区域用户［3］，在随机FBS 的覆盖范围内按硬核泊松点分布，其中热点区域用户占比为a。FBS 覆盖范围外的用户由MBS 提供服务，依此将用户分为宏小区用户（Macrocell User，MU）和毫微微小区用户（Femtocell User，FU）。FU 可在保证MU 正常通信的情况下伺机接入MU 占用的频段。

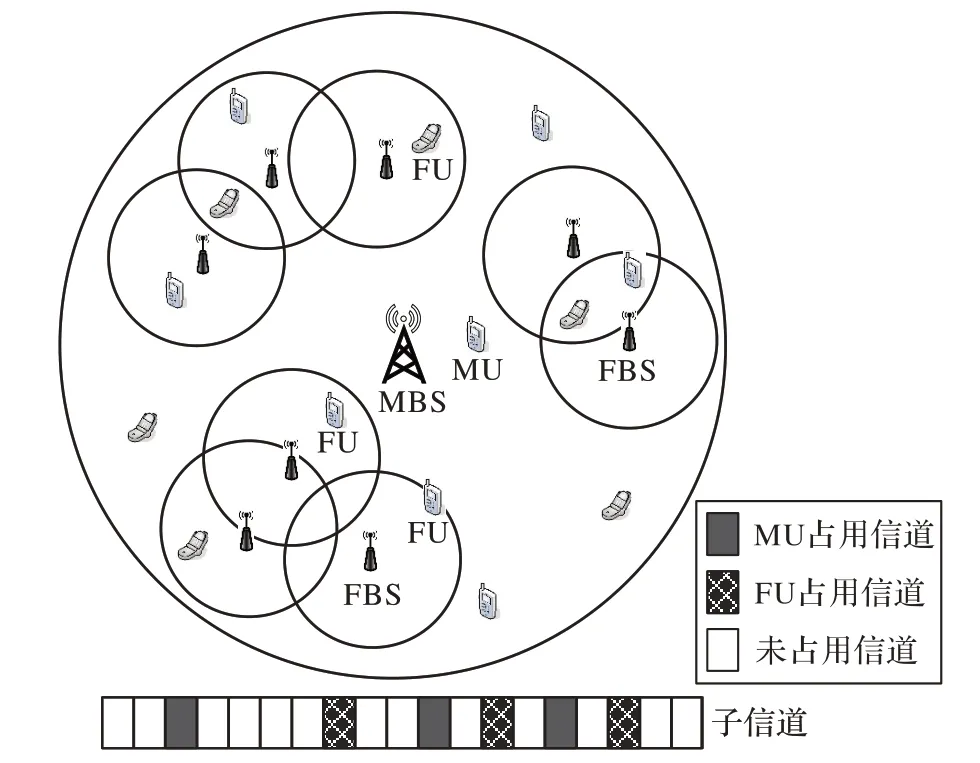
图1 异构认知超密集网络模型Fig.1 Heterogeneous cognitive radio ultra-dense network model

可将用户n的信干噪比rn表示为：

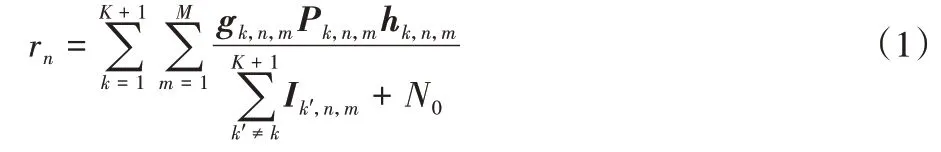
其中：gk，n，m表示基站用户信道的逻辑连接向量，当gk，n，m=1 时认为基站k用户n与信道m建立连接关系，为0 则未建立连接；Pk，n，m为基站k在信道m向用户n发射的功率；hk，n，m为增益，有：

其中：wk，n是基站k到用户n的大尺度衰弱，与基站用户间的距离有关且成反比；Gk，n，m为小尺度衰弱，对不同的k、n、m是独立的同分布复高斯随机变换；Ik′，n，m为用户n受到来自基站k′造成的同频干扰。

其中：N0为高斯白噪声。由于异构网络中基站发射功率的量级差别，为保障资源分配阶段的公平性，本文引入MBS 补偿系数mr，有：

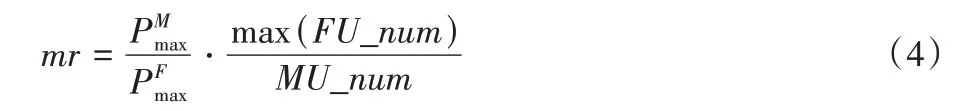
其中：补偿系数mr的含义为MBS 最大发射功率与FBS 最大发射功率之比与单FBS 小区内最大用户数与MBS 用户数比值之积。当信号的发射基站为MBS 时，为其发射功率乘上补偿系数mr。

1.2 问题描述

1.2.1 目标函数

本文将对异构CR-UDN 进行联合优化用户关联与资源分配，并将网络中总吞吐量作为目标函数。据香农公式，当载波间隔为W时，目标函数可写为：

1.2.2 基站连接上限约束

基站连接的用户数需小于等于天线数Lmax，需满足：

1.2.3 用户接入约束

本文为以网络为中心的模型，信道接入方式为正交频分复用（Orthogonal Frequency-Division Multiplexing，OFDM），即同一时间一个用户仅可与一条信道一个基站连接，需满足：

优化问题可建立为：

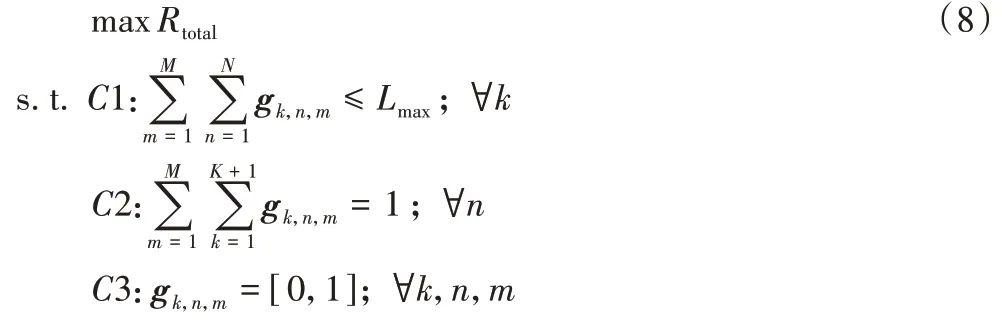
其中：C1 表示单基站最大连接数约束；C2 表示用户仅与一个基站和一个信道建立连接关系；C3 表示g为基站-用户-信道的是否建立连接关系的三维0/1 矩阵。该问题是一个三维非线性混合整数规划问题，是一个离散的NP（Non-deterministic Polynomial）难问题，求解难度较高。本文将通过确定基站-用户和用户-信道的匹配关系，最大化网络总吞吐量。

2 基于改进遗传算法的联合优化算法

该优化问题为一个三维的非线性离散优化问题，直接求解难度较高；故本文以最大化网络总吞吐量为目标，提出一种改进的遗传算法对上述问题中的用户关联与资源分配进行联合优化。本文算法的主要思路与改进如下：

1）预处理。构建用户可用基站链表和用户可用信道链表。

2）编码。采取符号编码，三维匹配信息拆分为用户-基站和用户-信道两个二维匹配信息。

3）适应度计算。计算网络中总吞吐量。

4）选择。依据适应度择优保留一部分个体，其余部分使用轮盘赌保留，在保证种群多样性的前提下提高了收敛速度。

5）交叉。采取多点随机交叉算子。

6）变异。加入早熟判决算子，防止算法陷入局部最优。

2.1 预处理

受文献［12，18］的启发，5G 时代的FBS 使用毫米波频段，具有视距传输（Line Of Sight，LOS）的特性。如图2左侧所示，将在用户视距范围内的基站定义为该用户的可用基站，而非视距传输（Non Line Of Sight，NLOS）范围内的基站为不可用基站，若视距传输范围内无可用FBS，则该用户由MBS 服务（MBS 默认编号为1）；不同用户因其运营商、办理业务的差异，有其对应的可用信道。如图2 右侧所示，建立用户可用基站和可用信道列表，并保证每个用户至少有一个可用基站和可用信道，预处理操作将解空间缩小为所有可行解的集合。用户终端（User Equipment，UE）作为MU和FU的统称。

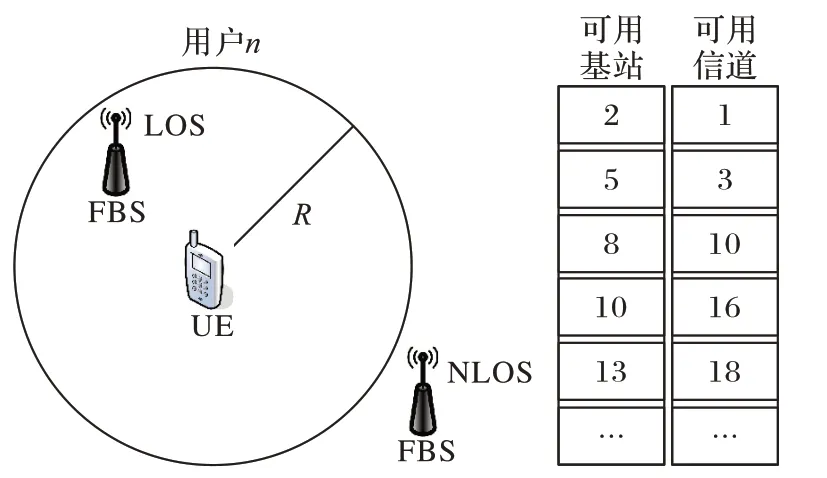
图2 预处理Fig.2 Preprocessing

2.2 编码

本文为以基站为中心的网络，具有一用户仅连接一基站、一信道，而同一基站或信道可被不同用户复用的特性。故采用符号编码，针对两种资源分别建立一条长度为N的数组BU和UC，每个数组的下标为用户编号，数组中所填符号为对应用户选择基站/信道的编号，如图3 所示。

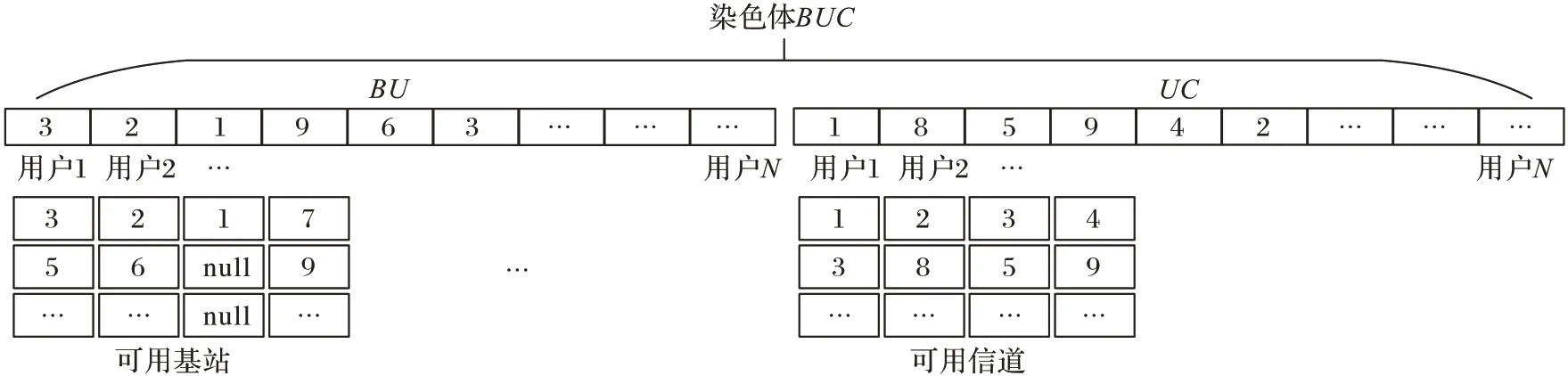
图3 符号编码Fig.3 Symbol coding

例如BU（1）=3，表示用户1 与基站3 建立连接关系。UC（2）=8，表示用户2 与信道8 建立连接关系。BU和UC中的序号取自2.2 节预处理中生成的可用基站和可用信道列表。将BU与UC合并为一条长数组BUC作为算法的染色体输入，每一条染色体均表示一种用户关联和资源分配的方案。

相比使用二部图或者0/1 编码的遗传算法，符号编码冗余较小，且本文的编码方式使得搜索空间为全部可行解，染色体基因与每个用户有直接的对应关系，确保每个用户均能分配到可用资源。相比0/1 编码的传统遗传算法，本文算法不会将迭代次数、交叉操作、变异机会浪费在不合约束的种群中（即出现一用户多基站或者用户分配不到基站的情况，尽管可以通过添加惩罚函数使得这些情况的适应度值足够低，但交叉变异操作后仍可能出现不合约束的染色体）。

2.3 低复杂度的适应度函数

遗传算法通过适应度函数不断筛选优质群体［19］，从而使种群不断进化，适应度越高，该染色体被选择保留至下一代的概率越大。本文采取系统内FU 总吞吐量作为适应度函数。传统遗传算法在计算效用前，有一染色体解码的步骤，即将每条染色体映射回基站-用户-信道关联矩阵。参考式（1）（3）（5）可见，同频干扰Ik′，n，m是吞吐量计算的一个难点，无法直接使用矩阵乘法求出。为计算同频干扰需搜索每一个用户所在信道以及使用该信道的所有用户，再搜索这些同频用户的服务基站到当前用户的增益，其中搜索同频用户的操作中出现了大量重复操作，时间复杂度较高。本文将所有用户吞吐量之和的计算改写为所有信道吞吐量之和，在不改变适应度计算结果的前提下降低计算复杂度，且不对染色体做映射处理，种群适应度计算步骤如下。

1）搜索染色体的UC部分，记使用信道m的用户集合为rum。

2）搜索BU部分找到rum的对应基站集合rbm，求得该信道下对rum中所有用户的期望增益hn′和除用户集rum的服务基站外的所有rbm到rum中每个用户的干扰增益之和Ithn′，如图4。

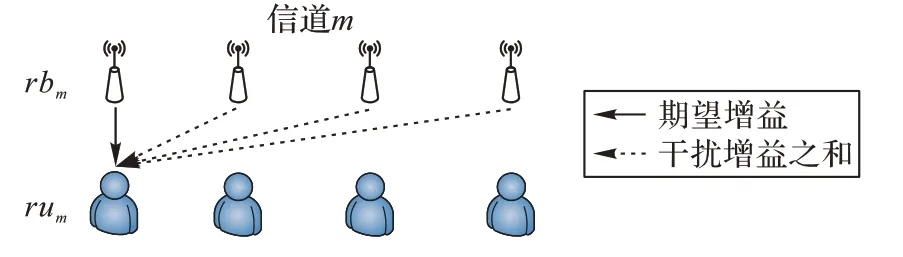
图4 同信道吞吐量计算Fig.4 Calculation of throughput in the same channel

3）按式（9）计算信道m内所有用户的吞吐量Rm。

4）按式（10）对所有信道的吞吐量求和。

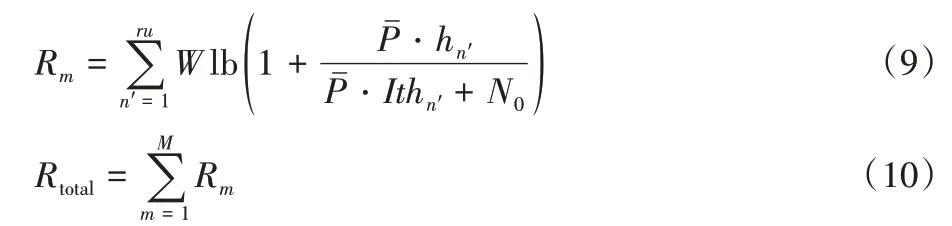
其中：为FBS 的平均发射功率，当信号的发射基站为MBS，为其乘上MBS 补偿系数mr。本算法使得在计算单个信道的吞吐量时只需搜索一次该信道内的同频用户，极大降低了时间复杂度。

2.4 选择、交叉与变异

1）选择算子——动态择优保留+轮盘赌。

选择算子依据适应度挑选优秀个体。由于遗传算法不依赖梯度等辅助信息，且本文处理的是非连续离散问题，收敛困难。加上该问题种群适应度无明显差异，仅使用轮盘赌选择算子效率较低；而仅采用择优保留的精英主义［11，16］又容易使种群过早收敛，陷入局部最优。综合两种方法的利弊，本文在选择阶段采取动态择优复制保留+轮盘赌选择机制，进行选择操作时挑选子代中最高适应度的染色体复制G_num条保留至新种群，为确保新旧种群规模相同，剩余L_num-G_num条采用轮盘赌抽取保留。本文将G_num设为变量，与当前迭代次数有关，有：

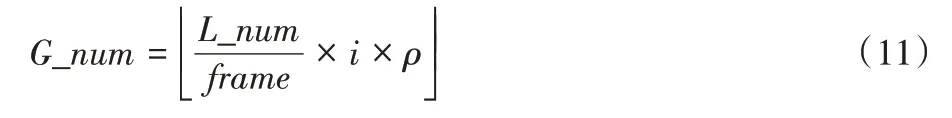
其中：L_num为染色体条数，frame为总迭代次数，i为当前迭代次数，ρ为0～1 中的择优比例常数,为向下取整。设计该动态的择优保留策略能保证在迭代前期仅牺牲较少种群多样性，在后期收敛至一稳定值。

2）交叉算子——多点随机交叉。

遗传算法中的交叉算子提供全局搜索性能，本文采取多点随机交叉作为交叉算子，当两条染色体满足交叉条件时，选择p个随机不同位置进行交叉，p的取值为1～2N中任意值。为防止交叉操作陷入循环，所有染色体经过交叉判决后，将种群中所有染色体的顺序随机排列。

3）变异算子——早熟避免。

变异算子为遗传算法搜寻提供局部搜索性能，本文采用位移置换作为变异算子。当满足变异条件时，将染色体的当前资源改写为该用户可用资源链表中当前资源的下一个资源（见图3）。考虑到存在可用资源数量仅为1 的用户，进行变异判决时将跳过这些用户，如图3 中的BU（3）。由于选择阶段采取了启发式算子，可能会使结果过早收敛。为了避免出现早熟而陷入局部最优，在变异阶段开始前，添加一个早熟判决，当同时满足下列两个条件时，认为出现早熟，开始动态调节变异概率Pm。

①当前迭代次数i还未达到迭代上限frame的一半。

②种群适应度最大值与平均值之差小于一阈值。

当上述两个条件均满足时，每迭代一轮，即倍增当前变异概率（满足Pm＜1），迭代至不满足上述条件时停止倍增操作，并复位变异概率，如图5。

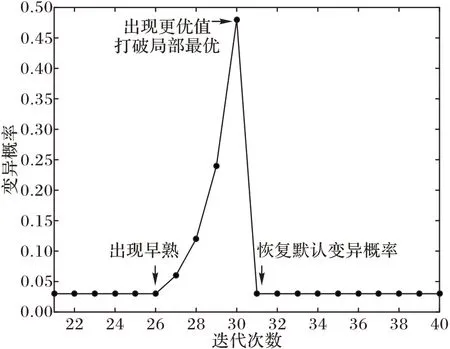
图5 避免早熟的变异算子Fig.5 Mutation operators for avoiding premature

本文算法框架与迭代过程如图6。

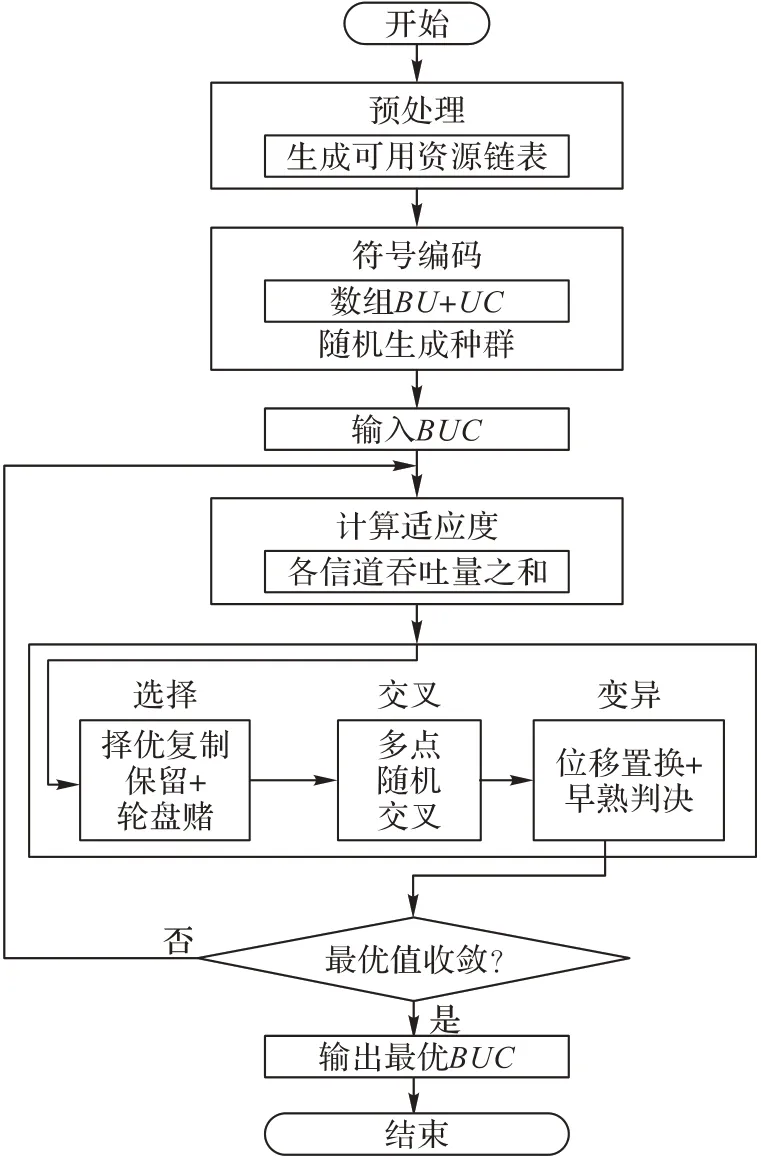
图6 联合优化算法框架Fig.6 Joint optimization algorithm framework

3 仿真分析

为验证本文算法的有效性，将本文算法与文献［16］的三维匹配的遗传算法、传统遗传算法（使用符号编码），文献［12］二部图+文献［20］图着色的两阶段算法进行对比，并对比仿真结果。仿真中默认设置1 个MBS，20 个FBS，50 个用户，20 条信道。遗传算法中包含300 条染色体，200 次迭代，500 次重复实验，假设认知基站完美感知信道状态，参考文献［3-4］，仿真参数如表1。

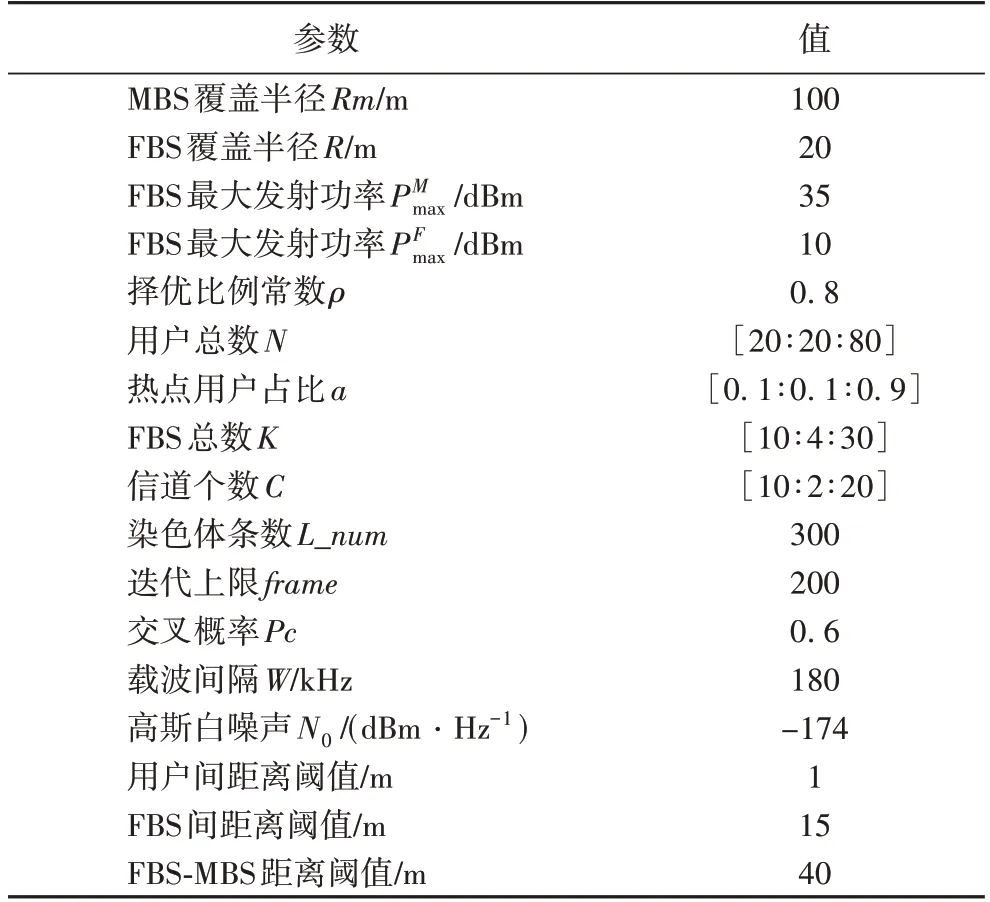
表1 仿真参数Tab.1 Simulation parameters

3.1 有效性分析

仿真图7 表示用户规模从20～80 变化与系统吞吐量的关系，迭代趋于平稳时说明收敛到最优值。系统吞吐量随用户数量的增长而提高，迭代平稳所需的迭代次数也随之增加。这是由于用户数量N的增长直接延长了染色体长度（染色体长度为2N），解的搜索空间呈指数增长，收敛所需迭代次数增多。用户数量的增加导致了更多的同频干扰，故吞吐量增长趋势会逐渐趋于平缓。

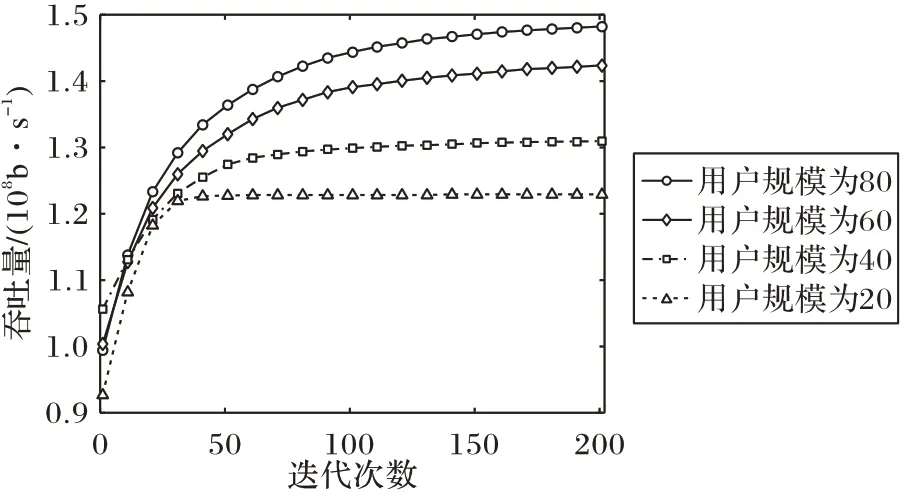
图7 迭代次数随用户数而变化Fig.7 Number of iterations varying with user number

图8 为不同变异概率下吞吐量的变化，可见适应度函数随变异概率的增长有一个先增后减的趋势。变异算子为遗传算法提供了局部搜索能力，变异概率Pm过小，获得变异机会的基因少，局部搜索能力弱，需要更多迭代次数寻找最优解；Pm过大，染色体大范围出现变异，可能导致潜在的最优解被破坏，导致系统难以在迭代上限次数内收敛。图像在区间0.02～0.04 趋于平稳，在0.03 处存在峰值，故本文将0.03 设为默认变异概率。

图8 吞吐量随变异概率而变化Fig.8 Total throughput varying with probability of mutation

系统总吞吐量的比较如图9 所示，比较随着热点区域用户占比a的提高，本文算法与其他三种算法在系统总吞吐量上的变化。

热点区域用户的占比a，即FBS 服务对象占总用户数的比例。由图9 可见，系统内总吞吐量随着a的提高而提高；这是因为将MBS 用户卸载至距用户更近的FBS 减小了同频干扰。此外，分步算法的吞吐量随热点用户占比的增长快速接近传统遗传算法；这是因为当a越接近1，FU 数量越多，该网络模型就越接近同构网络，这体现了图着色算法在同构网络中低复杂度高性能的优越性和在异构网络中的局限性。本文算法与其他两种遗传算法在a较低处（即更接近异构网络时）仍有较高的吞吐量，这是由于联合优化算法具有更强的全局搜索能力，不易陷入局部最优；而遗传算法是一种基于种群随机搜索的算法，对于各种类型的网络模型有较高的普适性。加上本文在适应度计算阶段考虑到MBS 与FBS 发射功率的差异性，引入了MBS 功率补偿系数mr，使得本文算法对异构网络具有更强的适应性。

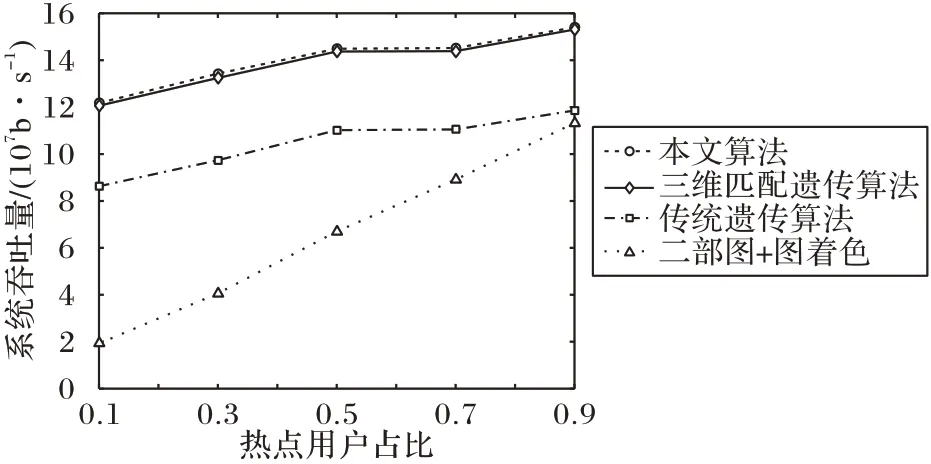
图9 总吞吐量随热点用户占比而变化Fig.9 Total throughput varying with the proportion of users in hotspots

图10 为FU 吞吐量随信道数增长的变化，可用信道的增加，降低了系统中的同频干扰，FU 吞吐量与信道数成正比关系。可以看到本文算法略优于三维匹配遗传算法与传统遗传算法，明显优于传统遗传算法和二部图+图着色的分步算法。经计算，本文算法比上述算法在总吞吐量方面分别提高了7.2%、43.5%和132.0%，在认知用户吞吐量方面分别提高了1.23%、34.3%和195.0%。这是由于处理的是非连续离散问题，传统遗传算法在选择阶段未保护最优值，且染色体间的效用值无明显差别，轮盘赌选择算子效率较低，收敛较慢，未能在迭代上限及时收敛至最优值，而本文采取动态择优保留+轮盘赌的策略，保护了种群多样性同时提高了收敛速度；三维匹配的遗传算法采取启发式的择优保留的策略，但是没有考虑启发式算子导致的早熟问题，针对该问题本文加入了早熟判决算子，检测到早熟时，将在每次迭代后倍增变异概率，直至出现更优值；分步算法由于单一优化的局限性，其性能远不如联合优化算法。可见本文算法对FU吞吐量的提升具有显著的优势，全局搜索性能更强。

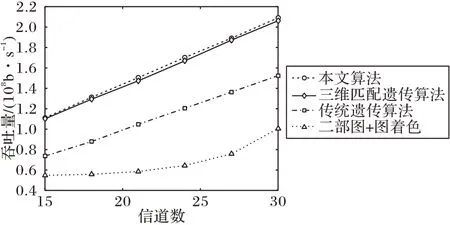
图10 FU吞吐量随信道数而变化Fig.10 FU throughput varying with the number of channels

吞吐量与FBS 分布密度的关系如图11 所示，三种方法的吞吐量均呈增加的趋势。当FBS 密度较低时，存在大量MBS 用户，同频干扰严重；随基站密度增加，MBS 用户逐渐选择接入FBS，降低了MBS 层的同频干扰；在实现全覆盖的基础上基站密度继续增加，大范围出现FBS 覆盖范围的重叠，用户有机会选择距离更近的FBS 接入，跨层干扰降低，因距离产生的衰弱减小，吞吐量继续增加。

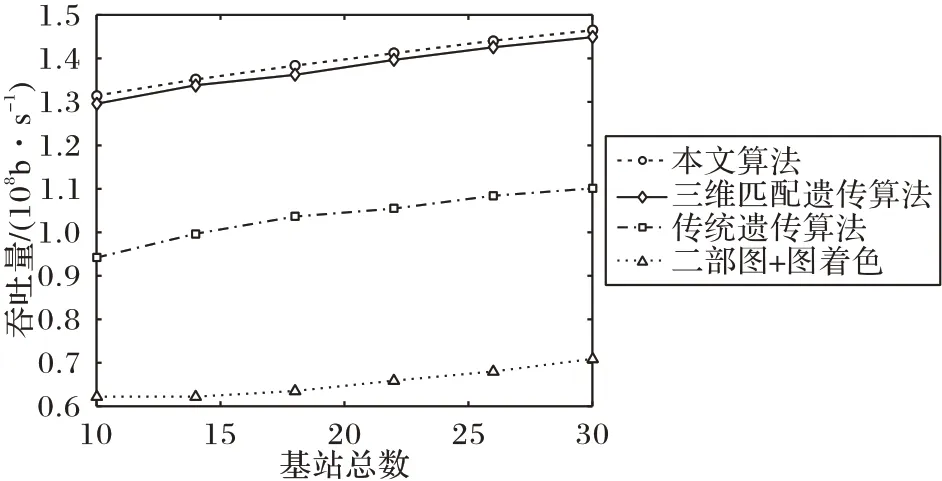
图11 FU吞吐量随FBS分布密度而变化Fig.11 FU throughput varying with FBS distribution density

3.2 算法复杂度分析

本文在计算适应度时将计算所有用户吞吐量之和改写为所有信道吞吐量之和（见2.3 节），避免了计算同频干扰时重复搜索同频用户的操作，降低了适应度计算阶段的复杂度。本文算法的各个阶段的复杂度如下：适应度计算O(L_num·C·N)；择优操作O(L_num)；交叉操作O(L_num·N)；变异操作O(L_num·N)，共经历frame次迭代。故本文算法的计算复杂度可表示为：O(frame·L_num·N·C)。

文献［16］的三维匹配遗传算法和传统遗传算法由于在适应度计算阶段的解码处理和累加用户容量导致复杂度较高，该阶段的复杂度为O(L_num)+O(L_num·N2·C·K)，复杂度之和均可表示为O(frame·L_num·N2·C·K)。

分步优化算法中文献［11］二部图和文献［20］图着色算法的复杂度之和为O(K·N+C·N)，复杂度较低；但由于将用户关联与资源分配拆分成了两个子问题分别优化，其吞吐量远小于联合优化算法。

其中L_num为染色体条数，frame为迭代次数，N为用户总数，C为信道总数，K为FBS 总数。

通过分析异构CR-UDN 模型中用户规模、热点区域用户占比、信道数量、FBS 分布密度对系统总吞吐量和FU 总吞吐量的影响，本文算法在收敛速度、计算复杂度上要优于文献［16］的改进遗传算法，相较于传统遗传算法不易陷入局部最优，在对异构网络的适应性上要优于二部图+图着色的分步优化算法。

4 结语

本文针对CR-UDN 异构网络总吞吐量优化进行研究，提出一种联合优化用户关联与资源分配的改进遗传算法。首先构建用户可用基站链表和用户可用信道链表；其次采取符号编码，将染色体分为用户-基站部分和用户-信道部分；然后以信道为单位计算适应度函数，采用动态择优复制+轮盘赌进行选择保留；最后将多点随机交叉作为交叉算子，并设计了避免早熟的动态变异算子。本文算法避开了传统遗传算法解码时的映射问题，使得解合乎约束的同时保证了迭代时的种群多样性和收敛性，避免了遗传算法的早熟问题；相较于图着色算法，本文算法在异构网络中有良好的适用性。仿真结果表示，本文算法有较好的收敛性，大幅提高了网络的吞吐量；然而在以提高吞吐量为目标的多约束优化问题中，用户关联、资源分配的优化与功率分配的优化有较强的耦合关系。下一步工作将重点研究联合优化场景下用户关联、资源分配算法与功率分配算法如何更好地实现解耦。