深度学习的可解释性研究综述
李凌敏,侯梦然,陈 琨,刘军民
(西安交通大学 数学与统计学院,西安 710049)
0 引言
近年来,深度神经网络(Deep Neural Network,DNN)在计算机视觉、推荐系统、语义分割等众多领域得到了广泛的应用,并且表现出很好的性能。深度神经网络的快速发展依赖于以下几个因素[1]:1)数百万有标签的数据集的出现;2)图形处理器(Graphics Processing Unit,GPU)性能的不断提高;3)更好的模型调优策略。然而,随着深度学习的飞速发展,模型预测错误的情况时有发生。如果不能从人类的角度对模型决策进行理解,寻找更好的模型最终将沦为纯粹依靠经验来不断实验以消除误差的试错法。
另一方面,在很多对性能要求较高的关键领域,对模型的透明性和可解释性也提出了较高的要求。例如在医疗领域检测心率失常方面,心脏病专家的诊断会依赖于机器学习方法的结果,但可解释性的缺乏降低了临床医生对此类方法的信任;在无人驾驶领域,出于对高度安全性的需求,错误决策原因的未知性极大阻碍了深度学习模型的实际应用。由此可见,深度学习的可解释性研究具有深远意义。
目前已经有一些关于可解释性的综述文献,如陈珂锐等[2]根据可解释对象的不同,从模型、预测结果和模仿者3个方面对机器学习的可解释技术进行了总结和分析;化盈盈等[3]根据可解释性原理将现有方法分成模型内部可视化、特征统计分析和本质上可解释的模型三类;曾春艳等[4]从自解释模型、特定模型解释、不可知模型解释、因果可解释性四个方面对深度学习的可解释性进行了分析。本文对现有的一些可解释性研究成果进行整理,加入了对深度学习的简单介绍,使用新的分类标准,将可解释性研究分成8 个方面,分别对其进行介绍。
1 深度学习
深度学习是机器学习的一个子领域,指从已有的样本中学习到一般性规律,并将其应用到新的未知样本上的方法。早期的机器学习并不需要对世界的很多认知,就能得到异于常人的能力;然而,对于人脸识别、语音处理等任务,需要输入人类掌握的相关特征,这是困难且复杂的。为了解决这个问题,表示学习出现了,即让机器自主学习并获得所需要的特征;但是现实世界是很复杂的,同一个物体在不同的光照下会有不同的颜色,在不同的观察角度下又会有不同的形状,表示学习无法习得这样的高级特征。深度学习的出现解决了这个问题,深度学习具有多个线性或非线性映射,能够层层递进地学习到线条等简单特征,再根据这些简单特征构建复杂概念,达到近乎于人的识别能力。
1.1 网络结构
多层感知机(MultiLayer Perceptron,MLP)基于生物神经元模型,最典型的MLP 包括3 层:输入层、隐层和输出层,不同层之间是全连接的。卷积神经网络(Convolutional Neural Network,CNN)处理具有网格图案的数据(如图像),旨在自动学习特征的空间结构层次,通常包括3 种类型的层:卷积层、池化层和全连接层。循环神经网络(Recurrent Neural Network,RNN)会对前面的信息进行记忆并应用于当前输出的计算中,具有更强的学习能力。深度信念网络(Deep Belief Network,DBN)使用概率和无监督学习生成输出,从输入层开始将网络的相邻两层当作一个受限玻尔兹曼机(Restricted Boltzmann Machine,RBM)进行训练,之后将上一个RBM 的隐藏层当作下一个RBM 的可见层。生成式对抗网络(Generative Adversarial Network,GAN)[5],同时包含判别式模型和生成式模型,可以用于生成一个全新的不存在的图像。
1.2 激活函数
激活函数的主要作用是使网络具有非线性建模能力,常用的激活函数为:
1)Sigmoid 函数。Sigmoid 函数又叫logistic 函数,可以作为二分类的一类激活函数。Sigmoid 函数易于求导,但是在反向传播时容易出现“梯度消失”问题。
2)tanh 函数。tanh 函数也是一类常见的激活函数,与Sigmoid 函数相比,由于均值为0,具有更高的收敛速度,也会出现“梯度消失”的问题。
3)ReLU(Rectified Linear Unit)函数。ReLU 函数避免了“梯度爆炸”和“梯度消失”的问题,能有效地实现梯度下降和反向传播,是目前常用的一种激活函数。ReLU 函数还有很多变种,如Leaky ReLU、RReLU(Randomized leaky ReLU)、Noisy ReLU 等。上述激活函数的具体形式如表1 所示。

表1 激活函数的形式Tab.1 Forms of activation functions
1.3 损失函数
深度学习中,损失函数用来衡量真实值与预测值之间的不一致程度。训练过程中通过使用梯度下降等优化方法来最小化损失函数的值,进而得到高精度的结果。常用的损失函数有CrossEntropy、均方误差(Mean-Square Error,MSE)损失函数、log 损失函数、指数损失函数(Adaboost)、Hinge 损失函数等,它们的基本形式如表2 所示。

表2 损失函数的基本形式Tab.2 Basic forms of loss functions
2 可解释性定义及重要性
目前,关于可解释性并没有清晰的定义和目标。最早关于可解释性的定义是2017 年Kim 等[6]在ICML(International Conference on Machine Learning)上提出的“Interpretation is the process of giving explanations to Human”,也就是说,可解释性是一个让人类理解的过程。Doshi-Velez 等[7]定义其为“Interpretability is the ability to explain or to present in understandable terms to a human”。同年,Miller[8]给出了更进一步的定义,可解释性是人们可以理解决策原因的程度。这表明,可解释性的最终目的并非完全理解神经网络中所有的内部特征,而是能够定量地拆分出来多少比例的信息是可以解释的、多少比例的信息是不可以解释的、多少比例的信息是确实被网络建模的、多少比例的信息是基于已有的信息进行合理猜测的。只要尽可能地把可以解释的特征信息分离出来,得到一个定量分析,就可以建立相互信任的关系。
Molnar[9]详细阐述了可解释性的重要性。总结如下:
1)人类的好奇心。对于不透明的机器学习模型,人们会本能地思考为什么它的分类精度这么高?只有真正理解了它的机制,科技才能进一步发展。
2)人类对找到事物存在意义的渴望。当机器学习逐渐渗透到人们的生活中,解释其发生的原因就显得尤为重要。比如推荐系统,人们在被推荐某些产品时,渴望知道内部原因,从而对该推荐具有更高的认同感。
3)安全性。如果机器学习在安全系统的应用过程中发生失误,带来了巨大的危害;但人类却不了解其内部机制,无法解释机器学习的决策,那么对它的使用将是特别可怕的。
4)社会接受度。人们对于自己要使用的物品具有很强的防范性,只有一个能给出解释并被人们理解的产品才会有更高的社会信任度,进而有更好的发展和应用。
5)伦理道德。机器可能在学习的过程中学到种族歧视等偏见,而可解释性使得人们可以查找原因并及时对其进行修复。
3 深度学习可解释性研究现状
近年来,学者们提出了很多解释深度学习模型的方法。可解释性的研究从大体范畴上可分为被动解释、主动干预解释以及补充解释。根据是否需要改变网络结构或优化过程可将相关研究分为被动解释和主动干预解释。
1)被动解释方法。针对的是一个训练过的网络,所有的权值都是已经学习过的,该方法只是试图从中提取逻辑规则或一些可理解的模式。
2)主动干预解释方法。该方法需要在训练前做一些小的改变,比如引入额外的网络结构或者在训练过程中施加可解释性的限制,进而使网络变得更易于解释(如更像决策树(Decision Tree,DT))。
3)补充解释。将相关的领域知识(如信息论)整合到网络中,得到更多信息的解释和更好的可解释性,是一种新兴的解释思路。
3.1 基于隐层可视化的可解释性
理解神经网络的内部特征,一个自然的想法就是对隐层运用一些可视化方法生成有实际含义的人类能理解的图像。Zeiler 等[1]在2014 年提出反卷积(Deconvolution)网络模型,将中间层的特征图作为输入,经过解池-矫正-反卷积操作,逆向重构生成图片,突出显示输入图像中的哪些模式激活了特定的神经元,其中,由于卷积神经网络中的最大池化操作是不可逆的,故而解池过程只能获得一个近似的逆。具体方法为:执行池化操作时使用一组switch 变量记录下每个区域最大值的位置;解池时生成的特征图只需保证每个区域在之前记录下的位置是最大值,其他位置置0,解池操作的示意图如图1 所示。
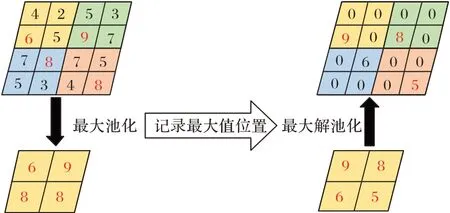
图1 解池操作示意图Fig.1 Schematic diagram of unpooling operation
2017 年Bau 等[10]提出了网络切割(Network Dissection)方法,该方法可以自动化地标定任意给定的网络内部带有语义的神经元,并通过计算隐层-概念对的匹配程度,量化分析了不同卷积网络内部神经元的语义特征。同年,Zhang 等[11-12]提出了解释图(Explanatory Graph)模型可视化滤波器。解释图中的每个节点严格表示某个子模式,每个边表示不同模式的同时激活关系和空间关系,进而将高层卷积层的混乱的知识表达拆分开来,并且具备了更好的可迁移性。
另一方面,由于神经网络在维数和观测量上的可扩展性,维数降阶也被应用于神经网络的隐层可视化。Aubry等[13]为了了解神经网络提取到的特征与自然图像中场景因素(比如物体样式、3D 视角、场景的照明配置等)之间的关系,使用主成分分析(Principal Component Analysis,PCA)对隐层的激活进行了可视化。Rauber 等[14]首次利用t-分布随机近邻嵌入(t-distributed Stochastic Neighbor Embedding,t-SNE)对神经网络隐层的高维数据进行降维,探索了神经网络学习到的观察表示之间的关系和人工神经元之间的关系。
基于隐层可视化的可解释性方法利用了网络内部隐层的信息,解释更有效;但有时隐层并没有特定的含义,主观性较强。
3.2 基于类激活映射的可解释性
类激活映射(Class Activation Mapping,CAM)的本质是对特征图进行线性加权来获得类别热力图,与原图叠加来可视化对预测输出的贡献分布。2015 年Zhou 等[15]提出了CAM,利用全局平均池化(Global Average Pooling)层代替全连接层,直接使用训练后全连接层上的模型权重。Selvaraju等[16]利用梯度信息,提出了梯度加权类激活映射(Gradientweighted CAM,Grad-CAM),对特征图的局部梯度求平均作为特征图的权重。Chattopadhyay 等[17]则认为梯度图上每个元素的贡献是有差异的,故而增加了一个额外的权重对梯度图的权重进行了二次加权,提出了Grad-CAM++模型。
以上3 种方法的内部机制如图2 所示,其中:表示特定类C的热力图在(i,j)位置上的值;表示类C在第k层的模型权重;表示第k层特征图的第(i,j)个元素;γC表示特定类C在全连接层的分数;Z表示归一化因子,是一个常数;表示类别C在第k层特征图的梯度图上二次加权的权重。
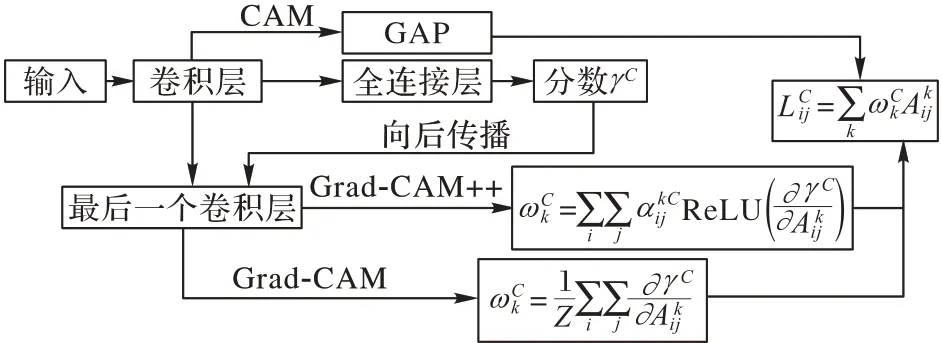
图2 三种类激活映射方法的内部机制Fig.2 Internal mechanisms of three class activation mapping methods
Wang 等[18]发现Grad-CAM 很容易找到错误置信度的样本,即部分权重较低的特征图获得了很高的置信度,而且局部的梯度存在饱和问题,受噪声影响很大,进而提出了一种不依赖梯度的权重表示方法(Score-weighted CAM,Score-CAM)。该方法定义权重为每个激活映射在目标类别上的前向传递分数。文中还提出了置信度提升(Channelwise Increase of Confidence,CIC),即:

其中:Al表示卷积层l的激活代表Al的第k个通道用Up(·)表示对上采样,s(·)为归一化 函数。式(1)表示将特征图上采样后,与原图像进行点乘,用处理后的图像响应与原图像响应之差表示该特征图的重要性。
同年,Desai 等[19]利用Ablation分析,提出了Ablation-CAM 方法。该方法遍历地将每层特征图置0 再进行网络前向获取目标类别得分,把该值与原始得分的相对大小作为权重。这5 种方法的优缺点如表3 所示。

表3 基于类激活映射的5种方法优缺点对比Tab.3 Advantages and disadvantages comparison among five methods based on class activation mapping
基于类激活映射的可解释性方法通过对特征图分配不同的权重来生成类激活图,实现了区域级的可视化,可以进一步区别分类;但它们关于权重的分配缺乏对应的理论基础。
3.3 基于敏感性分析的可解释性
敏感性分析(Sensitivity Analysis)是一类定量描述模型输入变量对输出变量的重要性程度的方法。神经网络的敏感性分析方法可以分为变量敏感性分析和样本敏感性分析。在变量敏感性分析中,基于偏导的敏感性分析方法利用不同隐层激活函数[20-22]的偏导数来评估输入变量对输出的影响。具体的细节如表4 所示。Dombi 等[23]提出了平均影响值(Mean Impact Value,MIV)方法,直接变动各个自变量的特征值,并按观测样本数进行平均,得到对应的输出的变化值,其绝对值大小表示变量的重要性程度。

表4 基于偏导的敏感性分析方法Tab.4 Sensitivity analysis methods based on partial derivatives
在样本敏感性分析中,Koh 等[24]利用影响力函数,刻画了对训练样本施加轻微扰动后特定测试样本损失函数的变化,来理解模型的预测效果。LIME(Local Interpretable Model-agnostic Explanation)方法[25]是一种与模型无关的局部近似。在关注的样本点附近进行轻微扰动后,探测模型的输出发生的变化,根据这种变化在兴趣点附近拟合出一个可解释的简单模型(如线性模型、决策树)。
Hui 等[26]认为负贡献可能不等于负相关性,需要在关联分解中分别处理正贡献和负贡献,提出了一种基于负特征和多数贡献的分解规则,能够同时提高网络中各属性的贡献对最终网络决策的敏感性和相关性,产生了良好的可解释结果。
基于敏感性分析的可解释性方法把解释性归因于输入特征或者样本,适合解释个体输入,但通常很难从中获得对网络的总体理解。
3.4 基于鲁棒性扰动测试的可解释性
鲁棒性即深度学习模型抵抗输入扰动并给出正确判断的能力。例如著名的对抗样本实验,将一个模型能正确识别的目标故意加上微小扰动后,深度学习模型就会给出错误的结论,这极大地增大了模型应用的安全隐患。因此,对模型的鲁棒性进行评估是很必要的,由此也发展出了很多基于鲁棒性扰动测试来解释模型的方法。
Gowal 等[27]利用简单的定界技术,即区间定向传播(Interval Bound Propagation,IBP),通过省略神经网络的最后一层线性层,提高了对单模型结构的验证精度;并且,由于IBP 的计算成本仅相当于网络的两次前向传递,可以执行更广泛的超参数搜索,进而训练大型的神经网络。
Pezeshkpour 等[28]提出了对链路预测模型的对抗性修改。通过对知识图谱的修改,识别出添加到知识图谱中的或者从知识图谱中删除的事实,这些事实能够在模型经过重新训练后更改对目标事实的预测。利用对图的删除,可以识别出对预测链接最有影响的事实来研究可解释性;利用对图的添加,评估模型的鲁棒性。作者设计了一种能够最小程度改变图结构使得目标事实的预测结果在重新学习后发生变化最大的方法,称为通过对抗性图编辑完成鲁棒性和可解释性(Completion Robustness and Interpretability via Adversarial Graph Edits,CRIAGE)。
Moshkovitz 等[29]发现真实数据是接近线性可分的,这一隐含特性可以同时使模型具有可解释性和鲁棒性。在决策树的背景下,提出了基于决策树的风险评分算法BBM-RS(learning Risk Scores relying on Boost-By-Majority)算法,利用本身就具有可解释性的风险评分模型,保证生成的分类器在具有较高的分类精度的同时,具有鲁棒性和可解释性。Koo等[30]探究了第一层的激活函数对模型的可解释性的影响,发现指数激活函数可以产生鲁棒的表示,而与网络深度无关。通过设置CNN 第一层的激活函数为指数激活,可以在激活前抑制背景,只传播有辨识性的信号,从而使第一层滤波器具有更好的可解释性,同时显著提高模型的鲁棒性。
Chen 等[31]提出了一种具有非负约束的深度矩阵分解(Deep Denoising Non-negative Matrix Factorization,DDNMF)模型,用于学习数据的鲁棒可解释的深度学习表示。具体地说,DDNMF 包含教师网络和学生网络两个部分。每个网络都包括一个编码器和解码器,其中:学生网络的编码器和解码器间包括一个非负矩阵分解(Non-negative Matrix Factorization,NMF)模块,接受并分解编码后的表示,再通过矩阵乘法恢复表示,以进行后续的解码,为模型带来可解释性;而教师网络抑制输入数据中的噪声。此外,通过定义一个可解释的损失,确保知识从教师网络转移到学生网络,增强表示的鲁棒性。
基于鲁棒性扰动测试的可解释性方法通过对精心设计过的新输入对模型预测的影响程度进行解释,为模型提供了安全保证,但这类举例的方法解释力最低。
3.5 基于频率原理的可解释性
对于传统的神经网络,参数越多,模型的训练精度越高,对应的泛化能力越弱;但是对于深度神经网络(DNN),其参数远远多于训练数据,然而DNN 在保持高训练精度的同时,泛化能力也很强。为了研究DNN 的泛化能力,2018 年,Xu等[32]提出使用频率原理(Frequency principle,F-principle)来解释神经网络,即在训练过程中,DNN 会先捕获低频分量,同时保持较小的高频分量,之后再缓慢地捕获高频分量。因此,对低频占优的目标函数及对象,DNN 往往具有较好的泛化能力;而对于高频占优对象,DNN 则具有较差的表现。这也能解释对低频占优的目标函数为什么提前终止训练能防止过拟合。
Xu 等[33]从傅里叶分析的角度,解释了训练好的DNN 在拟合奇偶函数时泛化能力差的原因。在理想条件下,从理论上证明了频率原理是由于激活函数的平滑性导致的,并将DNN 低频占优的原则和雅可比方法先收敛高频的特性相结合,加快求解泊松方程,为求解微分方程的数值解提供了新思路。Xu 等[34]利用频率原理,解释了为什么更深层的前馈神经网络训练更快。对于一个从隐层到输出层的子网络,其等效目标函数由隐层上一层的输出和真实标签构成。文中将整个神经网络分成pre-condition 和learning 两个部分,并着重分析了learning 部分的表现,发现更深层的神经网络的有效目标函数在训练过程中会更趋近于低频,再基于低频先收敛的F-principle,为更深的神经网络收敛更快提供了一种可能的解释。
Zhang 等[35]类比热力学系统,提出了线性频率原理(Linear Frequency Principle,FLP)模型,用一个简单的微分方程刻画了神经网络训练过程中的关键特征,在一定情况下可以定量预测神经网络的学习结果。FLP 模型只考虑网络参数的一些宏观统计量,忽略了单个参数的具体行为,这种刻画方式对准确理解DNN 的学训练过程提供了帮助,进而解释了DNN 在参数极多的情况下依然强大的泛化能力的原因。后续,Zhang 等[36]又将频率原理的内隐偏差作为两层神经网络的显式惩罚加以明确,利用FLP 模型准确预测了大宽度的双层ReLU 神经网络的学习结果,给出了泛化误差边界的先验估计,朝着定量理解一般神经网络的学习和泛化迈进了一步。
Luo 等[37]对一般DNN 的训练行为进行研究,通过一些适当的估计量刻画初始阶段、中间阶段和最后阶段的频率原理,建立了傅里叶分析的理论框架,发现DNN 的正则性转化为损失函数在频域中的衰减率,验证了频率原理的通用性,为更好地理解DNN 的训练过程奠定了频率原理的理论基础。Wang 等[38]注意到CNN 可以利用人类无法感知的图像高频信号,并探究了卷积核的平滑性和模型鲁棒性之间的关系,提出了帮助CNN 提高对抗鲁棒性的不需要训练或者微调模型的防御方法。
基于频率原理的可解释性方法对模型体系结构没有要求,但不容易合并特定领域的知识。
3.6 基于信息论的可解释性
解释深度学习的另一种方法是基于信息论的方法,其中著名的是由Tishby 等[39]在2000 年提出的信息瓶颈理论。文中把信号x中的相关信息定义为该信号提供的关于另一个信号y的信息,如面部图像提供的关于人名的信息。将x中所有与y相关的信息捕获,就可以任意压缩x而不丢失预测y的能力,即为x寻找一个能最大限度地保留y信息的短代码。理解信号x,不仅需要预测y,还需要知道x的哪些特征在预测中起作用,这与神经网络可解释的需求不谋而合。基于信息瓶颈理论,Tishby 等[40]在2015 年提出了信息平面,通过层间和输入输出变量之间的互信息来量化网络结构,进而产生了网络分层架构的一种可能的解释——最优的架构、层数和每层的特征及连接都与信息瓶颈权衡的分岔点有关,即输入层相对于输出层的相关压缩,层状网络的层次化表示对应于沿信息曲线的结构相变。
Schwartz-Ziv 等[41]发现深度学习训练过程中包含“特征拟合”和“特征压缩”两个阶段,并对信息平面中的DNN 进行了可视化。图3 展示了tanh、ReLU、PReLU 这3 种激活函数在基于随机梯度下降的训练过程中的信息平面,其中:横轴表示输入X和隐层T的互信息;纵轴表示输出Y和隐层T的互信息;不同位置表示了不同隐层保留的关于X和Y的信息的多少;一条线代表一轮迭代,随着迭代轮次的增加,颜色逐渐由深色变为浅色;每条线上的点代表不同隐层,右上角代表第一个隐层,左下角代表最后一个隐层。从图3 可以看出,第一层始终位于右上角,位置几乎没有变化,始终包含很多关于X和Y的信息,而深层最初包含X和Y的信息非常少,但随着epoch 的增加,所包含X和Y的信息也逐渐增多。根据其位置的变化,该过程可分为两个阶段:第一个阶段每个点都往右上角移动,表示隐层学习到了关于X和Y的信息,即“特征拟合”;第二个阶段向左移动,表示隐层逐渐减少关于X的信息,即丢掉无关信息进行“特征压缩”。
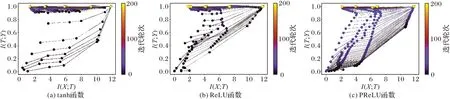
图3 三种激活函数训练过程中的信息平面Fig.3 Information planes in training process of three activation functions
针对难以通过增加网络参数观察到过拟合问题,Achille等[42]提出参数数量不能真正衡量神经网络的复杂程度,真正起作用的是网络参数中所含参数的信息量。利用权重中的信息来衡量学习模型的复杂性,为权重产生了一个新的信息瓶颈,并证明了网络表示学习成分的不变性和独立性是由权值中的信息限定的。Pimentel 等[43]将探针作为互信息的估计,引入了控制函数评估探针的有效性并进行了相应解释,反驳了“为了避免探针学会了任务本身,应该使用更简单探针模型”[44]的观点,给出了如何选择探针的建议。Bang等[45]以信息瓶颈原理为标准,提出了一种用于解释的变分信息瓶颈(Variational Information Bottleneck for Interpretation,VIBI)。对于每个实例,解释器返回一个概率,即是否将一个词、短语或句子(自然语言处理领域)或者一组像素(计算机视觉领域)等特征块作为解释选择,再将选定的特征块作为信息瓶颈来最大限度地压缩输入和输出之间的信息。该方法是系统无关的,可以解释任何黑箱模型。
基于信息论的可解释性方法将信息论领域的相关概念应用到神经网络,可以获得更多信息的解释,但在泛化到不同的网络结构时效果较差。
3.7 基于可解释模块的可解释性
基于可解释模块的可解释性研究构建了新的可解释的深度学习模型,促进了深度学习模型可解释性的进一步发展。
胶囊网络(Capsule)由Sabour 等[46]在2017 年提出。胶囊是一种新型神经元,输出一个有长度和方向的活动向量来表示一个整体或者整体部分,活动向量的范数(长度)代表它的置信度,方向代表实例化参数。胶囊神经元将输入向量v1和v2先做仿射变换,得到u1和u2;然后做加权和s=c1u1+c2u2,之后通过一个挤压方程(squashing function)v=得到输出向量v,其中,做加权和的系数c1和c2是通过动态路由(Dynamic Routing)机制得到的。动态路由使得每个胶囊能够编码一个特定语义的概念,可以清晰地知道每一个“胶囊”所做的工作。
可解释的基于候选区域的CNN(Region-CNN,R-CNN)是在2017 年由Wu 等[47]提出。R-CNN 由一个用于目标检测的区域建议(region proposal)组件和一个兴趣区域(Region of Interest,RoI)预测组件组成,其中RoI预测组件基于RoIPooling 算子对边界框建议进行分类和回归。为了使其实现弱监督自动化学习,作者提出了一个有向无环与或图(directed acyclic And-Or Graph,AOG)解析算子,并用其代替RoIPooling 算子;因此,在检测过程中,每个包围框都可以由实时从AOG 派生的最佳解析树进行解释。
Chen 等[48]在2016 年提出了基于信息最大化的生成对抗网络(Information-maximizing Generative Adversarial Network,Info-GAN)模型,能以完全无监督的方式学习解离化表征的生成对抗网络的信息理论扩展。Info-GAN 改进了GAN,将输入噪声向量分解为两部分,以此来最大化可以得到的互信息,从而实现更加具有可解释性的表示。Info-GAN 的基本结构如图4 所示,输入的噪声分为随机噪声Z和隐向量C,其中,隐向量C有先验分布,包含了生成数据的特征;然后通过生成器G 可以得到生成数据G(Z,C)。Info-GAN 要求生成数据和隐向量C之间有尽可能多的互信息,从而保证在生成数据的过程中损失的隐向量C中包含的信息尽可能少。同时,真实数据(X_real)和生成数据(X_fake)要经过判别器D 判断数据的真假,并根据互信息更新生成器G 和判别器D。

图4 Info-GAN的基本结构Fig.4 Basic structure of Info-GAN
Gu[49]提出了可解释图胶囊网络(Graph Capsule Networks,GraCapsNets),使用一个基于多头注意力的图池化操作替换基本路由部分。由于图池化操作揭示了哪些输入特征被池化为相关特征,故而可以很容易地解释分类决策。
基于可解释模块的可解释性方法可以更好地针对目标任务进行解释,但需要网络和解释模块之间的兼容性。
3.8 基于优化方法的可解释性
传统的统计机器学习方法结构清晰,深度神经网络性能优越,把现有的机器学习方法转化成等价的神经网络,就能兼具两者的优点。
最早的工作是Daubechies 等[50]提出的迭代收缩阈值算法(Iterative Shrinkage Thresholding Algorithm,ISTA),它是求解稀疏编码的优化方法中较著名的一个方法。在此之后,出现了很多对ISTA 的改进。Zhou 等[51]引入了一种新的自适应动量矢量到ISTA 中,并将其转化为一个循环神经网络,将对L1 范数的优化方法与LSTM 结合起来,提出了稀疏编码网络模型SC2Net(Sparse Coding to Network)。这种自适应的ISTA考虑了优化变量更新时每个维度之间的不同和历史信息,弥补了常见的对L1 范数的优化的部分不足。Gregor 等[52]将ISTA 展开到循环神经网络中,提出了学习的迭代收缩阈值算 法(Learned ISTA,LISTA)。Liu 等[53]提出了ALISTA(Analytic LISTA),只留下步长大小和阈值参数的数据驱动学习,大幅简化了训练,并具有与LISTA 相当的性能。
2015 年Zheng 等[54]把CNN 和条件 随机场(Conditional Random Field,CRF)概率图模型结合起来。具体地,将条件随机场的求解表示成RNN 的相关运算,构造了名为CRFRNN 的基本单元,将其作为CNN 的一部分插入网络结构中。在学习CRF 参数的同时,基于反向传播对整个网络进行端对端的训练,避免了后向处理,在图像语义分割上实现了突破。
Wang 等[55]提出了一种深度L0 编码器对L0 范数的稀疏逼近问题进行了优化。该编码器基于稳健迭代算法,通过引入新的神经元和池化函数,建模了一个前向式神经网络,拥有更好的学习能力,在分类和聚类任务中有很好的表现。Zuo 等[56]针对盲反卷积问题,将lp范数最小化问题的解,即广义阈值收缩(Generalized Shrinkage-Thresholding,GST)算子推广到p<0 的情况,提出了能实现稀疏编码的回复式神经网络。通过迭代指定的GST 参数,可以动态地实现显著性边缘选择和时变正则化,使得模糊核估计具有更好的鲁棒性。
2017 年,E[57]在其发表的论文中将深度神经网络视为离散的动力系统,通过数学推导,展示了使用微分方程解释深度残差网络(Residual Network,ResNet)。Lu 等[58]进一步表示很多深度神经网络都可以和常微分方程联系起来,利用数值分析中的结论,提出了一种线性多步体系结构(Linear Multi-step architecture,LM-architecture),可以在 任何类 似ResNet 的网络上使用,并且具有更高的精度。2018 年,Chen等[59]利用常微分方程(Ordinary Differential Equation,ODE)构造了一个新的深度神经网络模型ODENet。2019 年Grathwohl 等[60]对算法进行进一步改进,提出了可逆动力学自由形式的雅可比矩阵(Free-Form Jacobian Of Reversible Dyanamics,FFJORD)方法,降低了算法的复杂性。总体来说,基于ODE 的可解释方法中,将神经网络对隐藏状态的导数进行参数化,不需要再分层传播梯度与更新参数,大幅降低了存储成本。此外,由于网络的输出是通过计算常微分方程得到的,而现代ODE 的求解方法已经很成熟,这类模型的精度和速度也有较大提升。
另一方面,由于偏微分方程(Partial Differential Equation,PDE)在图像处理、计算机视觉等方面的优异表现,很多学者将PDE 与深度神经网络联系起来,也取得了很好的成果。2009 年Lin 等[61]设计了一种基于PDE 的神经网络模型,能较好地解决很多图像处理问题。2017 年Haber等[62]提出了使用PDE 来解释包括ResNet 在内的一类用于图像、语音、视频学习的高精度深度神经网络的方法。2020 年Ruthotto 等[63]将神经网络训练与PDE 约束优化联系起来,证明了PDE 约束优化中模型参数的正则化可以转化为神经网络输出的正则化,提出了一种基于拉格朗日乘子法的前向传播算法,使得模型在较少标签的情况下也具有较高的预测精度。
基于优化方法的可解释性方法拥有对目标任务更强的解释性,但受限于优化方法自身的某些不足,如利用范数实现稀疏性所导致的高昂的计算代价、方程解的稳定性等。
3.9 小结
本节从8 个方面对可解释性的研究现状进行整理,表5总结了这8 类方法的特点以及部分结合方法的描述。

表5 各类方法特点对比及结合方法描述Tab.5 Comparison of characteristics of various methods and description of combined methods
4 可解释性的评价指标
由于模型、规则和假设的多样性,截至目前,还没有出现一个统一且通用的可解释性的标准化指标。由于决策树方法是最具解释性的机器学习方法,一些方法通过对模型加以改动,使之更像决策树来增加模型的可解释性。通过评价模型的解释复杂性(Interpretation Complexity,IC),即模型中参数的数量来衡量这类模型的可解释性是一种直观且容易理解的指标。IC 值越低,模型越具有可解释性。文献[44]中采用了这种指标,表6 展示了其部分实验结果。
表6 中,对比对象包括和标准的决策树(DT)算法、鲁棒的决策树(Robust DT,RobDT)算法[65]、风险评分算法LCPA(Lattice Cutting Plane Algorithm)[66]和基于决策树的风险评分BBM-RS(learning Risk Scores relying on Boost-By-Majority)。对于DT 和RobDT 算法,IC 是树中内部节点的数量,对于风险评分(LCPA 和BBM-RS),它是权向量中非零项的数量。从表6 中可以看出,BBM-RS 算法在7 个数据集中的IC 值都是最低的,表明了结合决策树的风险评分算法具有更好的可解释性。
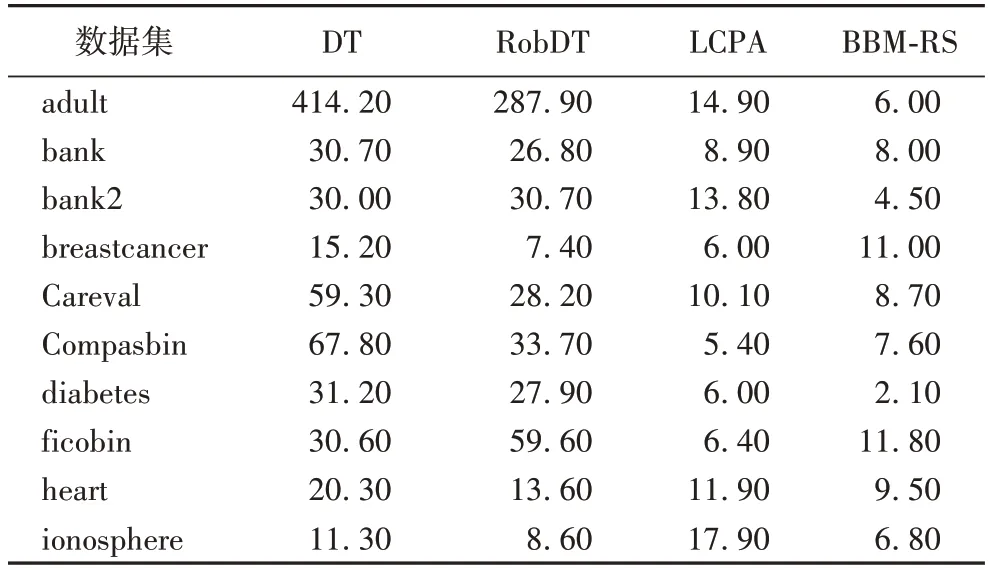
表6 不同算法的IC指标的部分实验结果Tab.6 Some experimental results of IC index among different algorithms
5 可解释性深度学习的应用
随着深度学习的可解释性研究的发展,越来越多的领域运用可解释的深度学习模型解决问题。
5.1 网络安全应用
研究发现,攻击者通常可以从中间层特征推断出输入信息。Xiang 等[67]提出了一种新型的隐私保护机制:将实值特征转化为复值特征,将输入信息编码隐藏在复值特征的随机相位,构建复值神经网络。在不同的数据集和网络结构上进行实验,结果表明该方法可以有效抵御各种攻击,保证用户信息的安全性且几乎没有精度损失。
另外,2019 年郭文博等[68]认为现有的应用于网络安全方面的深度学习模型可解释性极低,与网络安全本身需要的高透明度相矛盾,因此这些模型“不值得信任”;为此作者提出了非线性近似的局部解释方法(Local Explanation Method using Nonlinear Approximation,LEMNA),引入Fused Lasso 处理特征间的依赖关系,并将其融入到一个混合线性模型中来拟合局部非线性的决策边界,获得聚类该样本的重要特征作为解释。
Xu 等[69]在2021 年提出一种支持解释的软件复用检测(Interpretation-enabled Software Reuse Detection,ISRD)方法,从粗粒度到细粒度地捕获程序语义,使用包含功能层、基本块层和指令层的多层次标记模型来唯一标识程序,并构造函数调用图分析程序行为,使软件复用检测结果具有可解释性。
5.2 推荐系统应用
Lu 等[70]在2018 年提出了一种多任务推荐模型,可以从用户的评论中共同学习评级预测和推荐解释。具体地,使用矩阵因子分解模型进行评级预测,使用序列到序列学习模型进行解释生成。该模型通过增强解释生成过程,解释了用户对某一物品看法的潜在原因。
树增强嵌入方法(Tree-enhanced Embedding Method,TEM)[71]结合了基于嵌入的模型和树模型的优点。首先利用树模型学习显式的决策规则(又称交叉特征),然后使用嵌入模型合并交叉特征进行预测。核心是引入嵌入技术和注意力机制代替原本的全连接层,保留了模型的可解释性,从而使推荐过程是完全透明和可自我解释的。
2019 年一种用于从用户行为中学习非纠缠表示的宏观-微观解离化变分自动编码器(Macro-micro Disentangled Variational Auto-Encoder,MacridVAE)[72]被提出。宏解离通过了解用户意图,推断与其相关的高层次因素,捕获用户对不同高层次因素的偏爱。微解离通过VAE 对信息进行理论解释,使每个维度可以独立反映一个低层次因素。这一方法不仅在性能上取得了实质性的改进,并且是可解释和可控制的。
Ye 等[73]在2021 年提出了一种基于XGBoost 和注意机制的可解释推荐模型,解决了模型预测的自解释问题。从基于XGBoost 的树部分提取有效交叉特征,将结果输入到基于注意机制的嵌入式模型中,捕捉用户id、商品id 和交叉特征之间的不可见交互,用于预测用户和推荐项目之间的匹配分数。最后根据得分为不同的用户项目生成不同的推荐理由,在保证推荐性能的同时,提高了推荐理由的可解释性。
5.3 医疗应用
Biffi 等[74]在2018 年提出了一个三维卷积变分自编码器(Variational Auto-Encoder,VAE)模型,用于心脏病患者的医疗图像分类。该模型利用从3D 分割中学习到的可解释的任务相关解剖学模式(Anatomic Pattern),允许在图像的原始输入空间中可视化和量化所学习到的病理学特定重构模式。
2020 年Schaumberg 等[75]提出一种可解释的深度学习模型,开发了一种社交媒体上的机器人,使用机器学习分类器来帮助病理学家获得具有挑战性病例的实时反馈。如果病理学家在社交媒体上发布了一个病例,并@该机器人,则它会使用帖子中的病理文本和图像,生成疾病状态的定量预测,并实时搜索社交媒体和PubMed 的类似案例;同时发布摘要,通知分享类似病例的病理学家,病理学家之间随后展开更具价值的讨论。
2020 年Wang 等[76]提出一种使用胶囊网络的可解释深度学习架构(single-cell Capsule Networks,scCapsNet)。该模型通过识别竞争性单细胞类型,执行特征选择,进而识别编码不同类型亚细胞的基因组。
2021 年Pintelas 等[77]提出一种可解释的图像分类框架,用于皮肤癌的预测问题。该框架结合了分割和聚类技术来提取纹理特征,并过滤了高度相关和不太重要的特征,最后构建了一个全局的基于向量的特征层次树,用于为人类提供有意义和可理解的模型预测解释。
5.4 社交网络应用
对社交网络中谣言的真实性进行判别,可以通过适当的神经网络模型来实现。但由于神经网络本身的不可解释性,证据的发现过程也很难解释。Wu 等[78]根据谣言传播的“自证性”,即假消息的相关评论及转发中会出现能佐证其真实性的内容,将决策树模型整合到协同注意网络中,提出了基于决策树的协同注意网络(Decision Tree-based Co-Attention network,DTCA)模型,基于决策树发现证据并通过决策条件对证据的发现过程进行了解释。Lu 等[79]为了准确检测社交网络上的假新闻,尽可能准确地刻画其传播模式,提出了图感知协同注意网络(Graph-aware Co-Attention Network,GCAN)模型,通过展示注意力权重分布,根据源文本内容和传播用户的序列,直观地呈现出确定一篇报道为谣言时的证据——可疑转发者及他们关注的词语。
Ni 等[80]提出一个综合模型来描述社会影响疫苗决策的过程,将多准则信念模型与社会网络分析相结合,证明整个疫苗接种覆盖率主要取决于个人的信念和判断决策标准,从社会网络中个体自愿的接种行为解释了社会接种覆盖率。
6 结语
随着深度学习的发展,人们意识到深度学习的不可解释性带来的应用瓶颈,因此越来越多的学者开始了深度学习可解释性的研究。
本文从具体的文献出发,从8 个方面总结了现有的关于深度学习的可解释方法。其中,大部分的方法试图理解已经训练过的网络,尝试从中提取一些逻辑规则或人类可理解的模式,是被动的解释方法。基于隐层可视化的方法解释了隐藏层的意义,主要集中在计算机视觉领域,提供了全局的可解释性;基于类激活映射的方法对特征图分配不同权重生成类激活图,来解释个体的分类决策;基于敏感性分析的方法是一种模型无关的归因,常用来评估特征的重要性;基于鲁棒性扰动的方法是一种例子解释,解释一个新输入(比如对抗样本)对模型预测的影响程度。后3 类方法都提供的是局部的可解释性。
主动方法则需要在训练前做一些改变,例如引入额外的网络结构或修改训练过程。基于可解释模块的方法引入事前可解释的神经元或组件;基于优化方法的可解释方法利用传统机器学习的先验知识,修改网络结构,促使网络变得更加可解释。
从现有的研究情况看,可解释性仍有几个可能的研究方向。首先,主动的可解释性方法探索不足。对被动方法的一些分析也表明,神经网络不一定学习那些容易被人类理解的表征,如基于频率原理的方法,就研究了关于频率信号的规律这一人类不易理解的信息。因此,如何在不损害网络性能的前提下主动地使网络具有可解释性仍然是一个有待解决的问题。
另一个重要的研究方向是如何更好地将领域知识整合到网络中。可解释性是关于提供解释的,而解释建立在可理解的术语之上,这些术语针对特定的目标任务。现在已经有很多方法构造不同类型的解释,但解释中使用的与领域相关的术语仍非常简单,像素和颜色、材料、纹理等视觉概念(计算机视觉领域)以及词汇(自然语言处理领域)作为领域术语,构成了解释的基本单位。基于信息论的方法应用信息论相关的术语解释神经网络,提供了一种新思路。如果可以利用更多的领域/任务相关的术语,将获得更多信息的解释和更好的可解释性。

