支持隐私保护训练的高效同态神经网络

钟 洋，毕仁万，颜西山，应作斌，熊金波*

（1.福建师范大学 计算机与网络空间安全学院，福州 350117；2.福建省网络安全与密码技术重点实验室（福建师范大学），福州 350007；3.澳门城市大学 数据科学学院，澳门 999078）

0 引言

由于与生物神经网络具有十分相似的特性，神经网络（Neural Network，NN）一直以来都是业界的重要研究热点，并已在计算机视觉［1］、声音识别［2］、医疗诊断［3］等智能领域获得了广泛应用。云计算［4］技术进一步扩大了神经网络应用的发展规模。用户和企业可以将模型训练任务外包［5］给云服务器进行处理，进而节省了大量的计算和存储资源。然而，用户数据常包含大量的敏感信息，一旦数据管理权上移至云端，将会面临严峻的数据安全和隐私泄露问题。据英国《卫报》报道，剑桥数据分析公司在未经用户许可的情况下，盗用了近5千万份用户资料［6］。《华盛顿邮报》也曾透露，Zoom 会议软件存在严重的安全漏洞，数以万计的用户视频被上传至公开访问网页［7］。可见，第三方云服务器不总是可信的，直接将数据上传至云服务器存在泄露用户隐私数据的严重风险；因此，须将数据进行加密后上传，也意味着研究云计算环境下的隐私保护方案以确保数据的机密性、并兼顾方案的计算效率和模型精确度是至关重要的。

针对云服务器辅助下的数据和神经网络模型隐私泄露的问题，研究学者结合差分隐私、安全多方计算［8］、同态加密（Homomorphic Encryption，HE）等技术开展了大量的研究工作。本文主要关注基于同态加密的隐私保护神经网络研究。在面向神经网络的隐私保护预测方面，Xie 等［9］在理论上分析了低阶多项式近似表达非线性函数的可行性，并提出了一种基于层级全同态加密（Fully Homomorphic Encryption，FHE）的密态神经网络模型，实现了神经网络的隐私保护预测。Gilad-Bachrach 等［10］使用泰勒多项式近似计算神经网络中的非线性函数，并引入单指令多数据（Single Instruction Multiple Data，SIMD）机制并行处理加密数据，提高了隐私保护预测的效率。为了实现深层神经网络的隐私保护预测，Chabanne等［11］基于BGV（Brakerski-Gentry-Vaikuntanathan）-FHE构造了安全的批处理归一化层，并采用多项式逼近方法实现ReLU（Rectified Linear Unit）函数的安全计算，提出的方案适用于更复杂的图像分类任务。Al Badawi 等［12］改进了一种兼容图形处理器（Graphics Processing Unit，GPU）设置的BFV（Brakerski-Fan-Vercauteren）-FHE 方案，为隐私保护神经网络模型落地于实际应用提供了理论条件。

上述研究方案仅实现了神经网络的隐私保护预测［13］，无法对神经网络模型进行安全的训练和更新。Zhang 等［14］首次提出了基于BGV-FHE 的隐私保护神经网络训练模型，采用泰勒多项式近似计算ReLU 等非线性函数，在模型反向训练的每次迭代过程中，将更新后的加密模型权值发送给客户端解密后再执行下一次迭代运算，缓解了由深层同态密文乘法产生的噪声问题。Hesamifard 等［15］采用切比雪夫多项式近似计算ReLU 函数，一定程度上提高了非线性函数的拟合精度，且减少了乘法运算次数，在提出的PPML（Privacy Protection Machine Learning）方案中，额外设置了固定的噪声阈值，仅当密文乘法噪声达到该阈值后，服务器才会将加密模型返回给用户进行解密，有效降低了通信开销。然而，文献［14-15］需要用户参与整个加密训练过程，且使用密文乘密文（Ciphertext-Ciphertext Multiplication，CCM）乘法计算线性函数的效率较低，多项式迭代近似计算非线性函数的精度不 高。Bourse 等［16］使 用TFHE（Torus Fully Homomorphic Encryption）-FHE 和“自启动”技术在单服务器设置下提出了二值化神经网络的隐私保护训练方案。此外，Lou 等［17］进一步实现了BFV 密文与TFHE 密文之间的转换，采用BFV 密文计算线性矩阵乘法以及TFHE 密文计算非线性函数，并构造了相应的电路模块，在硬件上完成了神经网络的隐私保护训练。虽然文献［16-17］可以在单服务器上独立完成隐私保护模型训练，但该方案需要额外的自启动操作，非线性函数计算依赖于复杂电路，运行效率仍然较低。

上述方案采用同态加密技术实现了支持隐私保护训练的神经网络模型，初步解决了模型训练中的数据和模型隐私泄露问题；然而，文献［14-17］普遍存在模型训练效率和精度较低等问题。为了解决上述问题，本文提出了一种三方协作下支持隐私保护训练的高效同态神经网络（Homomorphic Neural Network，HNN），设计了一种安全快速乘法协议加速密文矩阵乘法计算的效率，研究了一种非线性函数的安全计算方法提高模型训练的精度。本文主要工作内容如下：

1）针对同态加密方案中密文乘密文（CCM）运算相较于明文乘密文（Plaintext-Ciphertext Multiplication，PCM）运算复杂度较高的问题，设计了一种安全快速乘法协议；通过向密文消息添加掩码后进行半解密将CCM 运算转换为PCM 运算，提高了计算效率。

2）鉴于多项式近似方法常被用来实现非线性函数的同态加密计算，研究了一种安全非线性函数计算思路，对添加掩码的消息执行相应的非线性算子，实现精确的非线性计算。

3）设计了一种三方协作的安全计算架构，并提出了一种支持隐私保护训练的高效同态神经网络（HNN），实现了安全前向计算、安全损失反向传播以及安全梯度更新。

4）理论层面证明了本文所提隐私保护训练方案及其协议的正确性和安全性，并提供了计算和通信的复杂度分析。采用MINIST 数据集的实验结果表明，本文方案的训练速度较于PPML 训练方案提高了18.9 倍，且测试集准确率提高了1.4 个百分点。

1 基础知识

1.1 全连接神经网络

全连接神经网络由输入层、隐藏层及输出层组成，每一层包含若干神经元，每个神经元由5 部分组成：输入、权重、偏置项、激活函数以及输出。若不考虑神经元的激活函数，神经元的表达退化为线性回归方程。此时，整个网络仅由多个线性回归组成，只能解决线性可分的问题。为了解决线性不可分的问题，须引入激活函数，例如ReLU 函数、Softmax 函数等。整体而言，全连接神经网络的训练过程可分为前向传播和反向传播。

1）前向传播。输入数据顺序经过若干个全连接层和激活层获得归一化的分类概率输出，网络第l层的运算可以描述为al=Wlxl-1+bl，xl=f(al)，其中：al表示第l层的神经元向量，Wl表示第l层和第l-1 层之间的权值矩阵，xl-1表示第l-1 层的输出（第l层的输入），bl表示第l层的偏置向量，f表示激活函数。

2）反向传播。反向传播根据链式法则计算目标损失函数关于模型参数的导数，并完成模型参数更新。若采用交叉熵损失函数作为神经网络的目标损失函数，令y表示神经网络的输出，label表示训练样本的真实标签，反向传播首先计算误差δl-1=(Wl)Tδl f′(al)，然后更新模型权值∂Wl=xl-1(δl)T和偏置∂bl=δl，其中：δl表示第l层的误差，∂Wl和∂bl分别表示权值和偏置的梯度，梯度的更新可表示为W=W-∂Wl·θ，b=b-∂bl·θ，θ表示学习率。

1.2 BGV同态加密

BGV［18］是一种 基于环 容错学 习（Ring Learning With Error，RLWE）［19］困难问题的全同态加密方案，能同时支持加法和乘法同态运算。BGV 加密方案包含参数设置算法Setup、私钥生成算法SecretKeyGen、公钥生成算法PublicKeyGen、加密算法Enc 和解密算法Dec。

1）Setup(1λ，uλ)：基于RLWE 困难问题，选择占u比特的密文模q和明文 模p，生成随 机参数d=d(λ，u)、N=N(λ，u)、n=n(λ，u)和χ=χ(λ，u)，满足2λ位安全；输出设置参数params=(q，p，d，N，n，χ)。

BGV 加密方案支持两种乘法运算类型［18］：明文乘密文运算（Plaintext-Cipher Multiplication，PCM）和密文乘密文运算（Cipher-Cipher Multiplication，CCM），具体定义如下。在BGV 方案中，密文由n阶多项式表示，密文模数为p，PCM 的计算复杂度为O(pn)，CCM 的计算复杂度为O(p2n2)。

定义1［17］已知明文消息m1和m2，c2表示m2的密文消息，如果同态运算⊙满足c2⊙m1=Enc(m1·m2)，称同态运算⊙为PCM 运算。

定义2［17］已知明文消息m1和m2，c1和c2分别表示m1和m2的密文消息，如果同态运算⊗满足c1⊗c2=Enc(m1·m2)，称同态运算⊗为CCM 运算。

2 系统模型与安全模型

本文方案的一个典型应用便是智慧医疗系统，越来越多的医疗机构采用AI 手段进行辅助医疗诊断，既能提高诊断效率又能提高诊断准确率。为了得到特定疾病对应的神经网络模型，这些医疗机构受限于技术设备问题而将病例数据交由云端，在云端完成目标模型的训练，机构获得所需模型后即能进行AI 医疗诊断；然而医疗数据含有大量敏感信息，直接在云端进行模型训练会存在隐私泄露风险，因而本文要解决的问题是如何让用户使用所拥有的数据在云端进行神经网络模型训练，且保证隐私数据和模型参数不会泄露给云端。具体系统模型和安全模型分别在2.1 节和2.2 节中介绍。

2.1 系统模型

系统模型在HNN 中，系统模型包含两台计算服务器S1和S2、一台辅助服务器S3以及数据拥有者Us，如图1 所示。

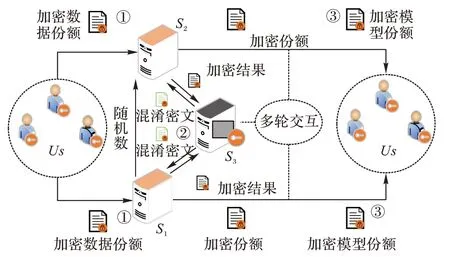
图1 系统模型Fig.1 System model

首先，S3生成公-私钥对(pk，sk)并发送给Us，同时将公钥pk发送给S1和S2；其次，实体间的交互过程描述如下：

①Us采用pk将数据加密后上传给S1和S2；

②S1、S2和S3协同执行隐私保护神经网络的训练过程，S1和S2均持有一份用户上传的加密数据份额，可以独自执行线性的密文计算，当执行非线性的密文计算时，S1和S2将添加随机掩码后的加密数据传递给S3，由S3采用sk对其解密后执行非线性计算；

③S1和S2将训练后的加密模型份额反馈给Us，Us采用加法运算可以恢复出完整的加密模型，然后解密获得真实模型。

2.2 安全模型

类似于文献［20-21］，本文采用半可信模型，每台服务器均是诚实且好奇的实体，诚实地遵循协议，但又对其他实体拥有的信息感兴趣。此外，假设服务器在计算过程中不能恶意掉线并提前终止协议，且服务器之间是不共谋的［21］，不能直接共享持有的秘密份额，这在实际中可由竞争型的服务提供商托管。数据拥有者旨在外包云端进行安全模型训练，因此用户是可信的，不会向服务器上传虚假的数据。模型采用安全信道进行通信，传递的消息不能被窃听和篡改。本文考虑下的隐私信息包含用户上传的数据、服务器协作训练的模型参数以及中间产生的计算结果。服务器S1和S2由于没有私钥，不能解密密文消息，S3不知道随机掩码，不能由混淆消息恢复出明文消息。

同时，模型引入一个概率多项式时间（Probabilistic Polynomial Time，PPT）敌手A*，在同态加密方案中常被认定为拥有多项式时间内的解密能力，正确识别两份密文对应的明文的概率不高于随机猜测的概率。假设A*拥有下述攻击能力和约束：①A*可能攻击S1或S2以猜测来自Us的密文所对应的明文值，也可能通过执行交互协议猜测来自S3的密文所对应的明文值；②A*可能攻击S3，通过执行交互协议猜测来自S1和S2的密文所对应的明文值；③A*不能同时攻击S1、S2和S3中的任意两方并获取相应数据。

上述敌手攻击能力的约束与文献［20-21］敌手约束是一致的，即敌手可以攻击单台服务器获取目标信息，但不可同时攻击任意两方服务器。该能力约束也是众多安全多方计算方案成立的前提，若无此约束，大多安全多方计算方案将无法安全执行，因此文中做出此类约束以保证方案的安全性。若服务器和敌手不能获得隐私信息，则意味着提出的HNN 方案在此安全模型下是安全的，详细的方案安全性证明过程如4.1 节所示。

3 HNN方案

HNN 方案的概述如图2 所示，包含全连接（Full-Connected，FC）层、ReLU 层和Softmax 层的安全前向传播和安全反向传播过程。在安全前向传播过程中，模型参数被随机拆分为两份模型参数份额，服务器S1和S2各自持有加密图像和一份模型参数份额，3 台服务器协作安全快速乘法协议（Secure Fast Multiplication Protocol，SFMP）可以实现FC 层中加密图像和模型份额的安全计算。接下来协同执行安全ReLU 协议（Secure ReLU Protocol，SRP），S1和S2向加密特征添加随机数，由S3对解密后的混淆明文特征进行非线性激活计算。类似地，3 台服务器协同执行安全倒数协议（Secure Reciprocal Protocol，SREP）和安全指数协议（Secure Exponent Protocol，SEP）完成安全Softmax 归一化操作。在安全反向传播过程中，3 台服务器负责协作计算FC 层、ReLU 层和Softmax层的加密梯度，然后结合链式法则与SFMP 协议完成加密梯度的安全传递和加密模型的安全更新，详细过程见4.4节。

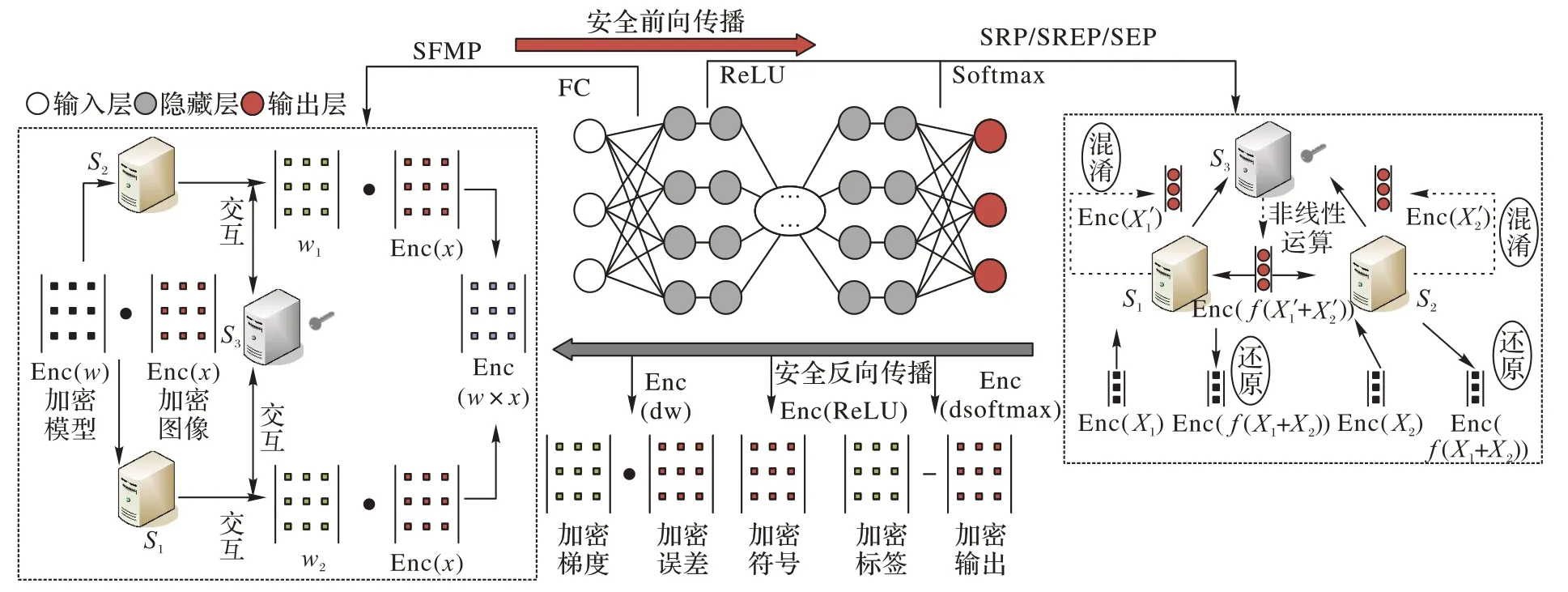
图2 HNN方案概述Fig.2 Overview of HNN scheme

3.1 安全FC层

FC 层负责计算输入特征与权值的线性组合，为了确保特征x和参数w的隐私性，文献［15］中采用HE 实现x和w的加密计算，但CCM 运算的复杂度较高。因此，本文结合加性秘密共享的思想，提出一种SFMP 协议，将CCM 运算转换为时间复杂度较低的PCM 运算，有效提高了FC 层线性乘法运算的效率。SFMP 协议的具体构造过程如协议1 所示。

协议1 安全快速乘法协议（SFMP）。

S1和S2持有加密参数cw和加密特征cx，S1向cw添加随机数k获得混淆加密参数temp。S3解密temp获得混淆参数m，并将m随机拆分为tw1和tw2，满足m=k·w=tw1+tw2。由于S3不知道k，不能推测出真实参数w。进而，S1和S2消除k可以分别获得真实参数的份额w1和w2，cw与cx的CCM 运算可以转换为w与cx的PCM 运算，即c1+c2=w⊙cx=cw⊗cx，其中w=w1+w2。

3.2 安全ReLU层

现有HE 方案［15］通常采用多项式迭代方法近似计算非线性函数，例如ReLU 激活层的比较函数，须执行多轮次的迭代运算减少计算误差。为了有效降低非线性函数的安全计算开销，本文设计一种SRP 协议用于实现高效且精确的安全ReLU 运算，具体构造过程协议2 所示。

协议2 安全ReLU 协议（SRP）。

Si，i∈{1，2}首先向加密特征份额ci添加随机数k获得混淆加密特征份额tempi，S3可以解密temp获得混淆特征m1，但不知道k不能获得真实特征Dec()。由 于m1=k·Dec(c)且k＞0，因此m1的正负性与明文特征Dec(c)相同，其中c=c1+c2。若m1≥0，则S3记录加密符号j←Enc(1)；否则S3记录j←Enc(0)。对于Si，i∈{1，2}而言，Si无法区分j是1 还是0 的密文。实际上temp⊗(1/k)=c，若Dec(c) ≥0，则SRP 协议输出激活的加密特征f(c)=Enc(0 · Dec(c))=Enc(0)；若Dec(c) ＜0，则SRP 协议输 出f(c)=Enc(1 ·Dec(c))=c。

3.3 安全Softmax层

在神经网络中，Softmax 层负责将网络输出特征归一化表示，已知特征x，Softmax 函数输出归一化特征为了保护特征隐私，本文设计SREP 和SEP 协议分别实现倒数和除法的同态加密计算。SREP 协议的具体构造过程如协议3 所示，Si，i∈{1，2}首先向加密特征份额ci添加随机数k获得混淆加密特征份额tempi，S3可以解密temp获得混淆特征m1，但不知道k不能获得真实特征Dec()。S3对m1执行相应的非线性倒数运算获得混淆倒数特征t←1(k· Dec(c))，从而Si消除k可以获得加密倒数特征f(c)=Enc(1Dec(c))。由于Si不知道私钥sk，无法解密获得真实的倒数特征1Dec(c)。

协议3 安全倒数协议（SREP）。

SEP 协议的具体构造过程如协议4 所示。类似于SREP协议，Si，i∈{1，2}首先 向ci添加k获得tempi，S3可 以解密temp获得m1=k+Dec(ci，sk)。S3对m1执行相应的非线性指数运算获得混淆指数特征exp(k+Dec(ci))，从而Si消除k可以获得加密指数特征f(c)=Enc(exp(Dec(c)))。由于Si不知道私钥sk，无法解密获得真实的指数特征exp(Dec(c))。

协议4 安全指数协议（SEP）。

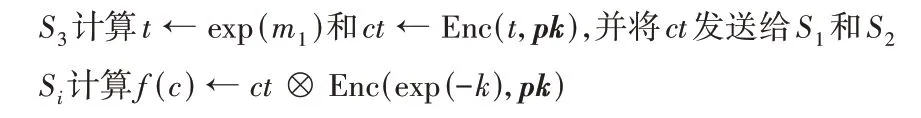
3.4 安全反向传播

HNN 训练过程如算法1 所示。数据拥有者Us将图像和模型参数加密后上传给云服务器，由S1、S2和S3协同执行HNN 的安全FC 层、安全ReLU 层和安全Softmax 层等前向计算和以及相应的误差反向传播过程。当达到迭代终止条件后，S1和S2将最优模型参数份额返回给Us，Us可以恢复和解密出最优模型参数{W*，b*}。

算法1 安全训练过程。

4 理论分析

4.1 安全性分析

本节主要分析HNN 方案及其安全计算协议的安全性，将用户数据、协议交互的中间计算结果以及模型参数的保密性作为安全评估指标。在安全性证明过程中，引入一组分别攻击Us、S1、S2和S3的外部PPT 敌手和内部服务器敌手(S1，S2，S3)。

命题1 面对半可信且不共谋的敌手A=和(S1，S2，S3)，SFMP、SRP、SREP 和SEP 协议是安全的。

SimUs接收输入w和x，然后模拟AUs：它产生密文cw=Enc(w)和cx=Enc(x)，并将cw和cx返回给AUs。AUs的视图由它创建的加密数据所组成，根据BGV 方案的安全性［15］，AUs的真实视图和模拟视图在计算上是不可区分的。

此外，3 台内部服务器S1、S2和S3也尝试推断获得隐私信息。S1拥有cw，cx和w1，但没有密钥无法解密获得明文模型参数w和数据x，S2类似于S1。S3可以采用私钥解密获得混淆明文m、tw1和tw2，但不知道S1随机生成的掩码同样无法恢复出明文w和x。因此，SFMP 协议可以抵抗A和(S1，S2，S3)的攻击。

同理可证，SRP、SREP 和SEP 协议面对半可信且不共谋的敌手和(S1，S2，S3)也是安全的。证毕。

命题2 面对半可信且不共谋的敌手A和(S1，S2，S3)，HNN 方案是安全的。

证明 若A攻击S1（或S2）并获取S1（或S2）的加密数据，BGV 方案的安全性可以确保A无法获取明文消息。此外，敌手只能获得明文消息的一份份额，秘密共享理论的信息论不可区分安全可以确保A无法获取完整的明文消息。若A攻击S3获取私钥并解密S3的加密数据，由于S1（或S2）传递给S3的加密数据均添加了随机掩码，A不知道随机掩码，无法获得真实的明文消息。由于S1、S2和S3间不能共谋，S1和S2无法获得S3生成的私钥并解密密文，S3也无法获得S1生成的随机数并恢复明文。A和(S1，S2，S3)均不能获得真实的隐私信息，可以证明HNN 方案是安全的。证毕。

4.2 复杂度分析

在本节中，主要分析HNN 方案及其安全计算协议的计算和通信复杂度。

计算复杂度 本文以简单全连接神经网络为例，输入k维数据，经过两层FC、一层ReLU 和一层Softmax，即k→(FC1+Re LU) →m→(FC2) →t→(Softmax) →t，获得归一化的分类概率。HNN 可分为安全前向传播和安全反向传播过程，假设Add 表示一次同态加/减法运算，CMult 表示一次CCM 运算，PMult 表示一次PCM 运算，Enc 表示一次加密运算，Dec 表示一次解密运算。安全前向传播过程的计算复杂度如表1 所示，安全FC 层采用SFMP 协议将CMult 运算转换为较低复杂度的PMult 运算，Add 运算用来完成神经元特征间的加法运算。安全ReLU 层和安全Softmax 层需要服务器S3辅助解密和加密，需要执行少量Enc 和Dec 运算。此外，由于非线性层的密文乘法次数较少，选择直接执行CMult运算。

表1 安全前向传播过程的计算复杂度Tab.1 Computational complexity of secure forward propagation process

假设n表示HNN 训练的小批量大小，安全反向传播过程的计算复杂度如表2 所示。安全Softmax 层的反向传播过程需要执行少量Add 完成归一化特征与样本标签的减法运算，安全FC 层需要执行PMult 完成一些乘法运算，安全ReLU 层的输出符号密文在前向传播过程中被记录，则不需要执行额外的运算。

表2 安全反向传播过程的计算复杂度Tab.2 Computational complexity of secure back propagation process

通信复杂度 由于HNN 方案是基于SFMP、SRP、SREP和SEP 协议构建的，本文主要分析这些基本安全协议的通信轮数及产生的通信开销。假设明文空间内的单位明文大小为‖P‖，密文空间内的单位密文大小为‖C‖，安全计算协议的通信复杂度如表3 所示。在SFMP 协议中，S1需要1 轮通信与S2共享随机掩码k，同时需要将添加掩码后的加密混淆消息temp传递给S3，S3可以解密获得混淆明文消息，并将两份加密份额tw1和tw2发送给S1和S2，协议共需要4 轮通信，通信开销为3‖P‖+‖C‖。类似于SFMP 协议，SRP、SREP 和SEP协议同样包含S1和S2共享随机掩码、S1和S2向S3发送加密混淆消息以及S3回传加密份额3 个阶段。

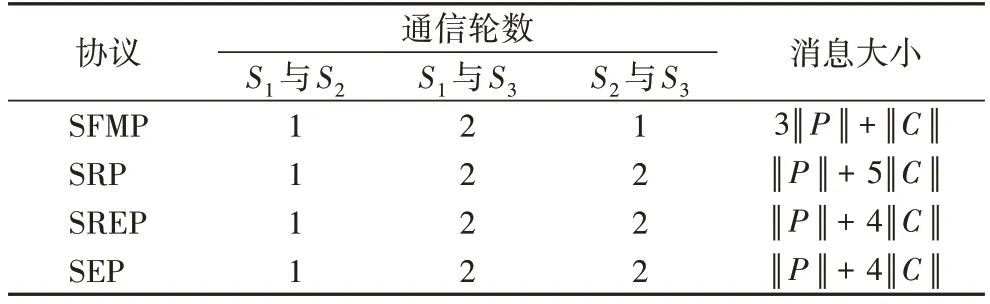
表3 安全计算协议的通信复杂度Tab.3 Communication complexity of secure computing protocols

5 性能评估

本文采用处理器AMD Ryzen 5 4600H 3 GHz，RAM 24 GB Ubuntu 20.0.4 的个人计算机模拟服务器，类似于PPML［15］、FHESGD（Fully Homomorphic Encryption Stochastic Gradient Descent）［22］和Glyph［17］方案，在C++开发环境下执行单线程的训练和计算。对于实数x，Helib 库截断保留x的k位小数，计算并存储x′=[x· 10k]，若x′＜0，则计算x′=(x′+p)modn，p表示明文空间的模，n表示密文空间的模。除非特别说明，实验设置64 比特表示明文消息，设置300 比特表示密文消息。实验采用HElib［23］库实现BGV 同态加密方案［17］，安全参数为128 比特。实验采用MINIST 手写数字集，包含0～9 这10 个类别，共60 000 张训练样本和10 000 张测试样本。选择5 种全连接神经网络模型进行实验，分别为N1（784 × 128 × 128 × 10）、N2（784 × 32 × 16 × 10）、N3（784 ×128 × 32 × 10）、N4（784 × 30 × 10）和N5（784 × 64 × 64 ×10）。激活层采用ReLU 函数，采用交叉熵损失函数计算网络目标损失，采用均值为0.1 的高斯函数随机初始化网络模型参数，学习率设置为0.6。

HNN 方案的安全性取决于BGV 同态加密方案的加密安全强度，这与安全参数的比特长度有关。选择N3 网络，表4给出了不同比特长度下单批量的HNN 方案训练时间结果。随着比特长度的增加，计算模数的增大会导致训练运行时间增加；另一方面，由于密文空间增大会降低随机识别密文的概率，使得HNN 方案的隐私保护强度也随之增强。因此在在设计HNN 方案时须兼顾同态加密的安全强度和效率。

表4 不同比特长度的HNN训练时间对比Tab.4 Comparison of training time of different bit-widths

FC 层涉及了大量的同态密文乘法运算，本文提出的SFMP 协议将CCM 运算转换为较低复杂度的PCM 运算，表5给出了不同乘法深度下CCM 和PCM 运算的计算开销对比。CCM 和PCM 运算的计算开销均随着乘法深度的增加而增加，乘法深度表示BGV 加密方案执行连续乘法而不导致计算错误的次数，与密文空间的模长呈正相关关系，这也意味着每条密文消息占用更长的比特位，执行单次乘法需要的计算开销越大。在同一乘法深度下，PCM 运算的计算开销只有CCM 运算的10%左右，表明SFMP 协议可以很大程度上提高隐私保护神经网络的计算效率。

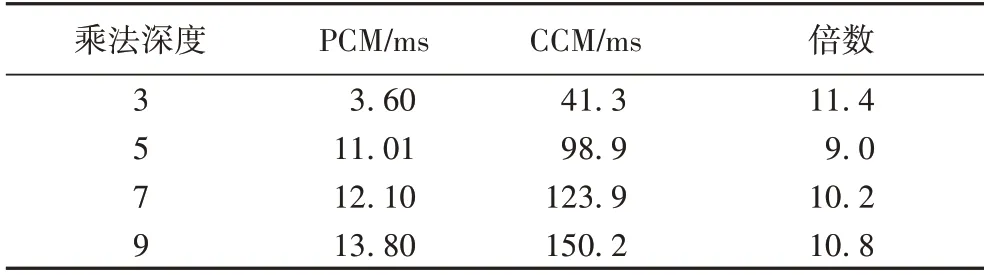
表5 CCM和PCM运算的计算开销对比Tab.5 Comparison of computational cost between CCM and PCM operations

隐私保护神经网络训练方案确保了数据和模型的隐私和安全性，但不可避免地降低了训练效率。采用N1、N2 和N3 三种神经网络模型进行实验，对一组小批量样本执行隐私保护训练，HNN 方案与相关方案的计算开销对比如表6所示。

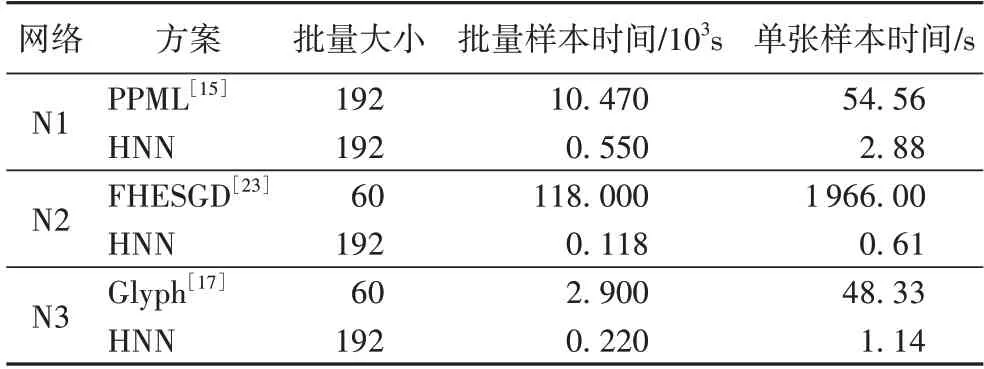
表6 不同方案的计算开销对比Tab.6 Comparison of computational cost among different schemes

基于双服务器架构的PPML 方案［15］采用CCM 运算执行FC 层中特征与参数的同态密文乘法，而本文的HNN 方案采用SFMP 协议将CCM 运算转换为PCM 运算，提高了FC 层的计算效 率，节省了 约94.7% 的训练时间。FHESGD［23］和Glyph 方案［17］不仅采用CCM 运算执行同态密文乘法，而且采用单服务器完成神经网络训练过程，需要额外的“自启动”操作来压缩加密乘法噪声，以确保同态计算的正确性。相比之下，HNN 方案牺牲少量通信开销，令服务器S3对混淆明文消息执行相应的非线性算子，不仅可以实现精确的非线性计算，而且大大降低了单服务器密文的计算开销。在N2 网络中，HNN 方案对批量192 张样本进行训练，消耗的计算开销远远低于FHESGD 方案［23］。类似在N3 网络中，HNN 方案训练单张样本的计算开销只有Glyph 方案［17］的2%。

上述结果表明HNN 方案的训练效率远远优于PPML［15］、FHESGD［23］和Glyph［17］方案。此外，本文给出HNN 方案与上述方案的模型精度对比，如表7 所示。经过5 轮迭代训练，Glyph 方案［17］的模型精度最高，达到96.4%，而HNN 方案达到相同精度仅需要3 轮迭代，与PPML 方案的95%准确率相比提高1.4 个百分点。这是因为其他方案只能采用泰勒多项式近似计算非线性函数，相较于明文环境下的神经网络训练会产生一些计算误差；而HNN 方案采用SRP、SREP 和SEP协议可以实现精确的非线性计算，因此可以更快地达到模型收敛效果。

表7 不同方案的模型精度对比Tab.7 Comparison of model accuracy among different schemes

为了观察本文提出的HNN 方案与明文神经网络之间的训练差异，采用N4 和N5 两种神经网络模型，设置批量大小为192，执行600 次批量迭代训练，HNN 方案与明文神经网络的训练模型精度曲线如图3 所示。在N4 网络中，HNN 方案的模型精度略低于明文神经网络，这是由于HNN 方案将模型参数由浮点型转换为整型产生的截断误差；但影响十分有限，在经过约280 次批量迭代后，模型精度趋于一致。N5 网络略复杂于N4 网络，在前160 次批量迭代中，HNN 方案的模型精度略高于明文神经网络，参数截断误差类似于向训练模型添加的噪声，反而增强了模型的泛化能力；经600 次批量迭代训练后，HNN 方案的模型精度近似于明文神经网络，可以达到96%。此外，HNN 方案的模型精度曲线的波动幅度明显小于明文神经网络，进一步验证了HNN 方案具有较强的模型鲁棒性。

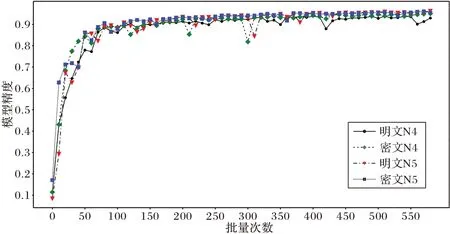
图3 HNN方案与明文神经网络的模型精度对比Fig.3 Model accuracy comparison between HNN scheme and neural network in plaintext environment

6 结语

本文提出了一种三方服务器协作下支持隐私保护训练的高效同态神经网络HNN 方案。针对现有方案计算效率较低的缺陷，设计了安全快速乘法协议将同态加密中的密文乘密文运算转换为复杂度较低的明文乘密文运算，提高了隐私保护神经网络的训练效率。为了解决多项式迭代近似计算非线性函数的计算误差问题，提出了一种多服务器协作的安全非线性计算方法，实现了非线性函数的精确计算。理论和实验结果均表明HNN 方案可以确保数据和模型的隐私性，训练效率和训练精度优于现有方案。在未来工作中，将基于全同态加密方案深入研究卷积神经网络和循环神经网络的隐私保护推理和训练方案，并探索密态训练方案移值于GPU设置下的可行性思路。