基于整体法的高中物理解题教学研究

刘丽娟

(江苏省徐州市丰县教师发展中心 221700)

新课改下的高中物理学科教学的目的及要求发生了深刻变革，其中最大的一个变化就是物理学科教学的根本出发点不再是教会学生求解物理考试问题，而在于有计划地培养高中生物理观念和物理思想等来促进他们物理核心素养的发展.然而，以往的物理解题教学中主要侧重“题海战术”训练，却没有考虑物理问题求解本质及相关求解思想的有效渗透及应用，以至于直接影响了最终的物理解题教学效果.此时加快革新物理解题教学方法，强化解题思想与方法的渗透显得尤为重要.

1 整体法及其在高中物理解题教学中应用的价值

所谓的整体法，是指在剖析问题的过程中可以立足于整个过程或者系统视角开展分析或研究活动的一种方法.整体法贯彻的思维过程是从局部到全局，是系统论中非常重要的一个思维方法，在力学分析领域中的应用尤为广泛.实际上，整体法是一种非常有价值的思维方法，在数学、物理等侧重思维运用的学科问题求解中具有广泛应用.基于整体法的灵活应用，可以从宏观或整体视角来对问题的变化规律或者内在本质进行揭示，避免中间无关紧要的繁琐计算环节，保证可以快速找到求解问题的突破口.因为基于整体法的有效运用，可以在受力分析过程中只考虑整体对象之外的受力情况，而不考虑整体对象内部彼此之间的相互作用力(内力).基于这种整体思维方式，可以在求解某些复杂物理问题过程中更好地对其中整体或者全过程受力情况进行明确，同时可以立足于整体视角来对事物变化规律和内在本质进行解释，很好地规避了中间无关整体计算的繁琐推理及计算过程，最终可以帮助学生快速求解物理问题.比如，在面对相对静止的系统受力分析时，可以灵活地运用整体法来对整个物理问题求解过程进行简化，保证快速帮助他们突破物理问题求解难关.与此同时，基于整体法的灵活应用，可以很好锻炼学生思维的灵活性，使他们不再局限于正向思维方式套用物理计算公式或模板来求解问题，而可以巧用整体法来对相关物理问题进行深入剖析.

2 整体法在高中物理解题教学中应用的策略

2.1 应用于受力分析题求解

受力分析题是一类最为常见的物理问题，实际的教学过程中要注意传授给学生一些针对性的受力分析技巧与方法，以此可以更好提高他们求解受力分析题的效率.而此时如果可以将整体法传授给他们，那么可以帮助他们在分析受力分析题的过程中对其中关键的受力分析对象进行明确，简化整个受力分析过程，避免因为过多干预因素而直接影响了受力分析的可靠性与有效性.

例1图1中的水平地面上搁置有一个大磅秤(秤②)，上面搁置一个大的木质箱子，并在箱子中放置一个小磅秤①，并且上边站立有一个人.在某一时刻该人发力向上推举木箱子的顶部，但是人和其他物体在这时候都保持静止状态，试求这时候大磅秤与小磅秤二者的示数会如何变化( ).

A.秤①和秤②的示数均增加

B.秤①的示数相应增加，秤②的相应示数不变

C.秤①的示数相应增加，秤②的相应相应减小

D.秤①的示数相应增加，秤②的相应相应增加

图1

解析本道受力分析题主要考查了高中生受力分析能力.在对问题进行剖析过程中，如果仅仅采取常规思路，那么由于整体图1中没有涉及到具体的受力大小数值，所以抽象性及繁杂性等特征比较突出，以至于直接增加了学生受力分析的难度.但是如果此时他们可以灵活地应用整体法来对问题进行剖析，那么就可以使他们更加准确地对整体和局部二者之间的相关性进行正确梳理.在对秤②示数变化情况进行分析过程中，可以将木箱子、秤①、人几个对象当成一个整体来进行分析，木箱子之内人向上推举箱子顶部的力属于内力，不需要进行考虑，所以这时候秤②本身的示数不会出现改变.而在对秤①的示数变化情况进行分析过程中，可以将人作为研究对象来对其向上推举木箱子顶部进行分析，此时必然会受到木箱子本身的反作用力，所以秤①本身的示数会相应地增加.基于整体法的灵活应用，可以快速确定本道题正确选项是选项B.

2.2 应用于多次作用题求解

多次作用方面的物理问题求解过程也非常繁琐，如果学生无法在分析问题中选对方法，那么不仅可能会涉及到繁琐计算，也可能会增加问题求解错误的出现概率.而基于整体法在物理问题求解中的有效运用可以对整个问题求解步骤进行简化，使他们可以在分析及解决问题中少走弯路，不仅提高了问题求解准确度与效率，同时也可以借此来帮助他们深刻理解相关物理问题的本质.

例2如图2，在某一光滑水平地面之上搁置5个质量相同的小物块，它们彼此之间间隔一定距离构成一条直线.然后给予第一个小物块一定的初动能E0来使其依次同剩余几个小物块相继发生碰撞，每次碰撞之后彼此不在分开.最后这五个小物块构成一个整体，试求此时其动能是多少？

图2

解析针对本道物理题的求解，如果学生求解中采用常规的思路进行剖析，那么需要对各个物体的碰撞过程进行逐一考虑，过程非常繁琐，尤其是在每一个碰撞环节中都需要有效地运用动量守恒定律来对问题进行剖析，整体求解过程非常复杂，浪费了时间不说，也增加了学生犯错的可能性.但是如果指导学生灵活应用整体法来剖析这道题目，那么就可以将这五个小物块看成一个整体.此时只需要进行简要计算即可快速找到最终问题的正确答案，而不必需要进行逐步分段分析，求解结果可靠性大大提升.

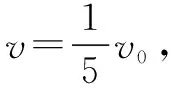
基于这种整体法的运用，可以将整个问题求解过程进行简化，保证学生可以准确求解问题，避免因为其中某个环节出错而影响了最终解题结果的准确性.

2.3 应用于简谐运动题求解

简谐运动也是一类高中物理问题求解中经常涉及到的物体基本运动形式之一，是高考考查的一个重要知识点.在求解相关物理类型题时，如果直接套用公式，那么问题分析起来可能同样比较复杂，难度较大.此时如果可以巧用整体法，那么可以帮助学生快速确定问题求解的突破口，尤其是可以联系实际的类型题来灵活地应用隔离法与整体法来巧妙地构建问题求解方程，那么就可以快速简化整个问题求解过程.

例3如图3，现有一个质量是M，劲度系数是k的弹簧振子，在某个时刻于振子上面搁置一个质量是m的小木块，使其可以和M一同于光滑水平地面上进行运动.已知小木块本身受到的回复力F满足F=-k′x，x是弹簧离开平衡位置处的位移量，试求k′/k的值？

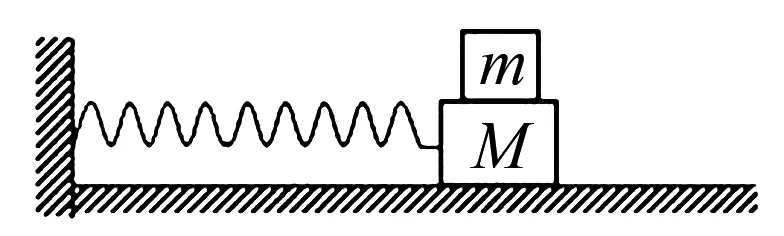
图3

解析略.

2.4 应用于物理综合题求解

在物理问题求解过程中，综合类物理问题也比较多见，会对学生思维的灵便性、解题能力等综合能力具有较高要求，单纯调用单一方面物理知识是无法求解相关物理问题的，必须要综合调用多方面的物理学科知识，借助逻辑思维、抽象思维等思维能力的有效应用，在整体法等解题方法的支持下来对整个物理问题求解过程进行简化，最终可以帮助学生快速确定问题求解的突破口与核心思路.但是必须要注意指导学生对整体法等一些有效解题方法的应用思路、流程以及注意事项等进行明确.

例4如图4，在某一光滑的水平面上搁置有滑块A、B和C，它们各自质量分别是2m、m和3m.已知其中滑块A和滑块B之间压缩有一个弹簧并借助不计重力和不可伸缩的绳子连接起来(注：弹簧与滑块A和B之间没有栓接起来).在最初的时候，滑块A和B均以相同初速度v0向右方移动，滑块C保持静止状态.某一时刻，连接滑块A与B之间的细绳突然断裂，滑块A和B被弹簧弹开，之后滑块B与滑块C之间发生碰撞并且粘结起来，最终3个滑块的速度恰好保持一致，试求这个运动过程中弹簧本身所释放出来的弹性势能同整个系统损失的机械能之比.

图4

解析略.

由此可见，基于整体法的灵活应用可以帮助学生仔细地梳理自己求解物理综合问题的思路，并且可以分别结合不同的研究对象来灵活地设计整体法应用的对象，保证可以通过灵活应用整体法、局部法等物理问题分析方法来对整个求解过程进行简化，力求可以快速、准确地确定问题求解的突破口，最终可以帮助学生迅速求解问题，提高了他们整体的物理问题求解能力.但是要注意的是对整体法应用于物理问题求解时必须要考虑它们彼此之间内力是否可以忽略，不能够任意选择两个物体当成一个整体来进行剖析，否则就可能会因为错误应用整体法而造成错解问题的出现.

总之，整体法是提高高中生物理问题求解能力的一种重要解题方法.在高中物理解题教学中融入整体法期间，要注意针对受力分析、简谐运动等不同类型的物理问题，灵活运用整体法来对整个问题求解过程进行简化，配合局部法等解题技法的灵活应用来帮助学生快速找到求解问题的突破口与思路，最终可以使他们运用整体法来快速解决相应物理问题.