高一学生数学抽象素养的培养策略研究
李春燕
(江苏省南京市江宁高级中学 211199)
数学抽象素养,指在数学学科中,完成对空间形式与数量关系的抽象.详细包括从具体事物中抽象出一般规律、在数或者图形关系中抽象出数学概念,然后用数学语言表征出来.数学抽象素养作为数学学科核心素养中的主要要素,能够反应学生数学学科知识本质的掌握情况.据此本文以概念课为例,结合高一学生数学抽象水平,提出几点教学策略.
1 高一学生数学抽象素养的培养
1.1 创建学习情境培养学生抽象思维
以数学概念为例,在教材中都是以简短的几句话进行描述,在严谨的语言下,表达知识的表象与本质,如果学生的抽象能力不足就会出现知识认知困难的问题.受构建主义理论的启发,教师在培养学生数学抽象能力的时候要尊重其主体地位,遵循学生的兴趣喜好,使用情景教学法,让学生在真实的情境中对话与思考,完成操作,建构意义,总结数学概念的规律与共性.因此,需要教师在教学中,针对概念的形成创建合理情境.情境构建的“数据库”要丰富多彩.教师作为引路者,要从具体案例中,引导学生找到数学有关的属性,然后抽象出数学概念,掌握本质,完成操作、过程、对象的阶段,经历抽象思维的过程.要注意的是,情境的创建不是教学目的,而是为了解决问题而服务.据问卷调查与访谈可知,高一的学生对于在复杂的情境中,抽离数学知识的能力还比较缺乏.所以教师可在学生理解知识点后,逐渐增加情境的复杂程度,以此锻炼学生的抽象思维,提升其复杂情境的理解能力,增强概念的解释能力.
1.2 创建思维导图助学生形成逻辑思维能力
数学的学习就是思维发展的过程,所以在此过程中学生的思维发展尤其重要.我们可以利用思维导图将学生思维可视化,完成对人脑思维方式的可视化模拟.高一学生的知识与技能维度的水平差距不大,表明其还能够通过有效的学习方式,掌握知识与技能.学生可以使用思维导图这种直观而又形象的方式,构建新旧知识的联系,进而建立对知识点的理解.如在经历一节概念课后,学生的思维可呈图示展示,这就是将思维外显与整合,可以助学生高效的掌握本节课重点知识.对于思维导图的运用,还要高中生经历客观感知与主观创造的过程.
第一,客观感知阶段中,需要教师在课堂结束后,呈现一节课教学知识的总结图示,在各种连线的牵引下,将所有知识通过一定关系连接起来并呈现,这样,学生可以结合自己所学,对本节课的重点知识与方法进行逻辑性的整理,挖掘逻辑思维潜能.
第二,主观创新阶段,在教师循循善诱的引导下,学生就可自主绘制思维导图,先找寻本节课学习知识的关键词,然后围绕知识与技能进行深入思考,有效加工,将涉及的内容通过线段连接,完成绘制,最后形成一幅完整的思维逻辑图,通过此过程不但能提升学生知识与技能的水平能力,还能形成逻辑思维能力.
1.3 引导学生多交流反思,培养数学语言能力
上面两个策略,体现在学生的思考与记录方面.其实数学语言的呈现才是体现学生数学思维的最佳载体.数学语言包括文字、图形与符号语言三种形态.数学文字语言抽象、数学符号语言简洁、数学图形语言直观.高中阶段,比较倾向于使用图形与符号语言.经过本人多年实践,发现高一学生的数学语言运用能力不强,经常有“不会用”、“不会说”的现象.教师要重视学生们的数学交流活动,以数学语言为载体总结数学学习的经验.在此教师要正确示范,引导学生反复练习,如让其上台讲解,开展分组讨论等,引导学生多说、大胆说,加强数学语言运用的规范性,对于不规范的语言,教师及时给予纠正.希望学生在多次练习中,完成数学文字向符号的转换.高中阶段数学的图形语言运用比较广泛,这也是数形结合的主要表达方式,可以借助图形的直观性与生动性、逻辑性发展学生思维.在师生之间与生生之间利用数学语言沟通,还能增强学生的数学抽象素养,快速完成抽象思维的形象化,能够在交流沟通中,科学反思,完善认知.在数学活动中,学生经过多次交流沟通,会逐渐实现从感知到认知,从认知到掌握,从掌握到运用,从运用到反思,进一步实践交流,反思与思维表达的完美融合,能够帮助学生构建新的认知结构.
例如,函数概念的教学中,为了让学生更好地理解“定义域指函数自变量x的取值范围,值域指函数值y的取值范围,一个x都有且只有一个y值与其对应”这段文字语言,教师就可引入符号语言,以集合N表示x的定义域,如x的取值范围大于2且小于5,以符号语言就可表示为定义域N={x|2 图1 学生在学习数学知识的时候,经历知识的生成与同化,在此要构建新旧知识间的联系,引向知识的同化.学生对知识同化的过程是知识形成的升华.在具体教学中,构建主义理论提出,教师要结合学生的已有经验、认知结构进行,助其在新旧知识经验的联合下,丰富学生知识体系.据调查,多数高一学生的知识同化能力都比较欠缺,说明其知识迁移能力比较欠缺.完整的知识同化过程为:教师给出知识的定义与定理,直接揭示知识本质,然后以旧的知识引导学生建立联系,完成知识内化与外延.接着在学生们同化知识基础上,向分化过渡,掌握新旧知识间的联系与区别.最后,将新学习的数学知识融入到学生已有概念体系中,完善知识结构.教师要多关注学生的知识迁移过程,把握旧知识中新知识的连接点与增长点,善用对比法,引导学生从同化到深化的过渡,尊重学生的主体性,让其有足够的时间与空间完成知识的迁移,科学辨别数学知识,抽象出数学知识,提升抽象素养. 以高一“基本初等函数(Ⅰ)”教学为例,阐述如何培养学生的抽象素养.具体教学过程为: 在情境教学中还可设计梯度性的问题,让学生从一般到特殊,经历知识抽象的过程,逐渐提炼出函数概念的基本属性.针对上面设置的不同情境,教师设置的数学问题为:一张纸折叠一次后,得到的厚度为多少个单位?折叠两次后得到的厚度为多少个单位?三次、四次呢?如果这张纸可以无限折叠,那么折叠x次后,他的厚度为多少个单位?一张纸折叠一次后面积是多少个单位?折叠两次、三次后呢?如果这张纸可以折叠无数次,那么x次后面积为多少?若将折叠后的纸的面积作为折叠次数的函数,求这个函数的解析式.在问题下引导学生观察思考与猜想,进而得到数学概念,在此过程中学生经历了完整的抽象活动,提升了数学抽象素养. 基本初等函数教学中,教师要引导学生抽象出函数的概念,以此培养其抽象概括的能力.当学生可以精准说出基本初等函数概念后,就可进行抽象理解了,这对于提升学生抽象概括能力有很大帮助.在此可经历实际案例,引导学生反复辨析,最终总结出基本初等函数的概念,完成对概念的同化理解.在了解函数概念之后,就可让学生继续交流思考,看是否可举出适合的例子,解释函数概念,有效提升学生的数学表达能力. 综上,如何快速培养学生的抽象素养,一直以来是教育研究者思考探究的问题,特别是高一学生的认知发展还是以形式运算为主,抽象素养的提升可助学生形成知识建构与迁移的能力.根据对学生数学抽象素养三个水平阶段的划分,让我们知道高一学生数学抽象能力的培养,与数学概念教学不能脱离.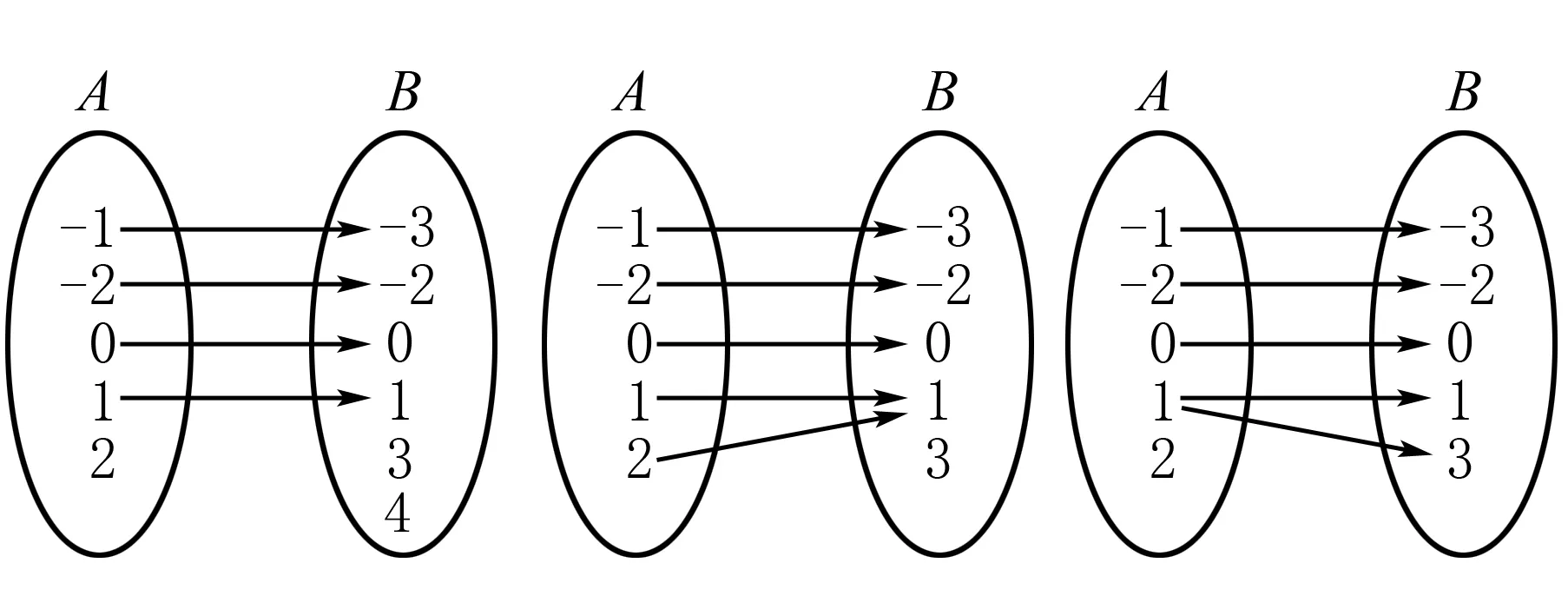
1.4 构建迁移知识体系,提升学生知识同化能力
2 培养高一学生抽象素养的案例分析
2.1 情境引入,初步感知基本初等函数概念抽象过程

2.2 巧妙设计问题,引导学生提取概念属性
2.3 由学生概括概念,在辨析中加深对数学知识的理解

