WSNs中基于测距修正和拟牛顿法的节点定位算法

孙 豫

(驻马店职业技术学院信息工程学院，河南 驻马店 463000)

0 引言

随着通信技术的迅速发展，无线传感网络(wireless sensor networks，WSNs)[1]已在环境监测、军事和医疗等领域广泛应用。WSNs中节点具有感测、通信能力。这些节点感测环境数据，如温度、湿度，并将所感测的数据传输至控制中心，以便控制中心进行处理。然而，只有明确了节点位置信息，其感测的数据才可能具有意义。因此，定位是WSNs的关键技术。

测距定位和非测距定位算法是主要的两类定位算法。不失一般性，基于测距定位算法精度高于非测距定位算法。常见的测距算法有：基于接收信号强度指标(received signal strength indication, RSSI)[2]、基于信号到达角度(angle of arrival, AoA)[3]、基于信号到达时间(time of arrival, ToA)[4]。与ToA和AoA不同，基于RSSI测距无需额外的测量设备，易实施。因此，基于RSSI测距定位受到广泛关注。

为了提高基于RSSI测距定位的精度，对RSSI值进行滤波处理。文献[5]提出双标签定位算法。该算法采用两个水平或者垂直定位标签，利用这两个标签所采集的RSSI值进行测距，进而降低RSSI因环境影响而产生的波动。然而，该算法需要额外部署一个标签，增加了硬件成本。

近期，由于微处理器数据处理速率和能力的提升，节点能够在较短时间内处理一定量的数据。因此，一些智能优化算法被用于节点定位。例如，文献[6]运用人工神经网络对RSSI进行预处理，降低测量RSSI值误差，进而提高测距精度，为后续定位提供准确的测距数据。文献[7]运用狮群优化算法估计节点位置。该算法的定位精度严重依赖于测距精度。若测距误差大，界定了搜索区域存在偏差，这就降低了定位误差。同时，节点端执行智能优化算法增加了节点能耗。

为此，提出基于测距修正和拟牛顿法节点定位(ranging correction and quasi-Newton method-based localization, RCNL)算法。RCNL算法先通过多次测量收/发两端间RSSI值，再利用正态滤波对RSSI值进行处理，剔除误差较大的RSSI值，然后进入定位阶段。定位阶段细分为两个子阶段：在第一个子阶段，未知节点利用RSSI测距，并利用这些测距构建搜索区域，再利用Bounding-box算法估计未知节点的位置，此次所估计的值为初始位置；在第二个子阶段，运用拟牛顿法校正初始位置的偏差，提高定位精度。性能分析表明，相比于同类算法，RCNL算法降低了归一化定位误差，提高了定位精度。

1 RCNL算法

1.1 RCNL算法概述

RCNL算法先对RSSI值进行滤波，再依据RSSI值估计收/发两端间距离(测距)。然后，依据这些测距数据作为Bounding-box算法的输入，输出为对未知节点的位置估计(初始位置)。考虑牛顿迭代法收敛速度依赖于初始值，将未知节点的初始位置作为拟牛顿法的初始值，再由拟牛顿法估计未知节点的位置。图1给出RCNL算法的总体框架。

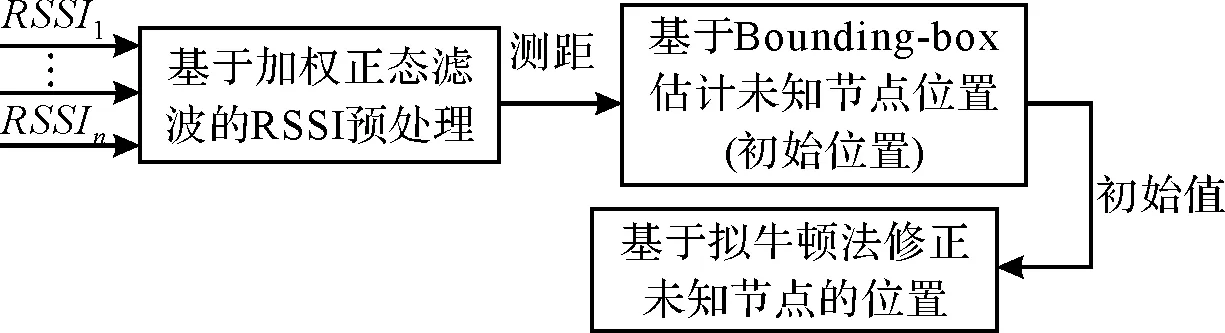
图1 RCNL算法框图

1.2 RSSI预处理

接收端记录接收信号的RSSI值，基于RSSI测距原理，利用RSSI值估算与发送端间距离，依据Shadowing的传播模型，可得收/发两端间距离关于RSSI值的关系式[8]：

(1)

式中：Pr表示接收端记录接收信号的RSSI值；Pt表示发射端传输功率；d0表示参考距离，通常取d0=1m；PL(d0)表示在参考距离条件下的路径损耗功率；χ表示测距噪声，其服从高斯分布。在理想测距环境，χ=0；d表示收/发两端间距离，如图2所示。

图2 信号传输模型

考虑到RSSI值易受外界影响，对RSSI值进行预处理，滤除偏差大的RSSI值，进而提高测距精度。多次测量的RSSI值应呈正态分布。利用正态分布的3σ原则[9]，可知信号分布在(u-σ,u+σ)区域内的概率约为0.652 6。其中u表示均值；σ为方差。

为此，RCNL算法先引用正态滤波策略滤除不在(u-σ,u+σ)区域内的RSSI值, 获取较准确的RSSI值。尽管引用正态滤波策略滤除了不准确的RSSI值，但其增加了算法的复杂度，将在2.5节中分析算法的复杂度。

然后，计算这组RSSI值的均值：

(2)

(3)

1.3 基于Bounding-box算法估计未知节点初始位置

Bounding-box算法也称包围盒算法，其是通过测量与锚节点间距离，并利用距离确定未知节点可能存在的矩形区。未知节点在多个矩形区域的重叠区域的概率最大。将重叠区域中心位置作为未知节点的估计位置。由于Bounding-box算法实施简单，RCNL算法引用该算法估计未知节点位置。考虑到Bounding-box算法定位精度不高，只将由Bounding-box算法估计的节点位置作为拟牛顿法的初始值[10]。

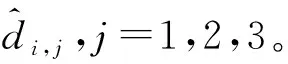
图3 基于Bounding-box算法示意图

1.4 基于拟牛顿法的节点位置修正

1.4.1 BFGS拟牛顿法

作为一种广泛应用的拟牛顿迭代法，BFGS算法是由Broyden, Fletcher, Goldfard和Shanno四人提出的牛顿法改进算法。BFGS算法通过迭代方式求解问题[11]。

令f表示关于未知变量的函数；X(x,y)表示未知变量。利用BFGS拟牛顿法通过式(4)求解变量X：

(4)

利用由正定矩阵B定义为Hessian矩阵的逆矩阵，即H-1=B。B的第k次迭代的值Bk为：

该桥东西两侧人行道铺装均存在纵向裂缝，这主要是由于人行道下板梁间未设铰缝连接，板梁间拼缝反射到人行道铺装表面所致。此外，人行道铺装还存在局部网裂和破损。

Bk+1=Bk+ΔBk

(5)

(6)

式中：

sk=Xk+1-Xk

(7)

yk=f′(Xk+1)-f′(Xk)

(8)

1.4.2 基于误差最小化的目标函数的构建

为了降低定位误差，将最小化定位误差作为目标函数：

f(x,y)=minE(x,y)

(9)

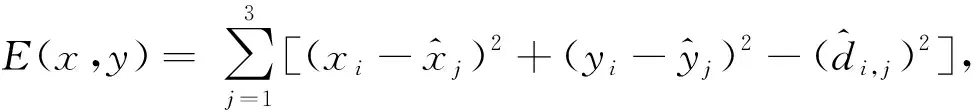
对E(x,y)展开，整理可得：

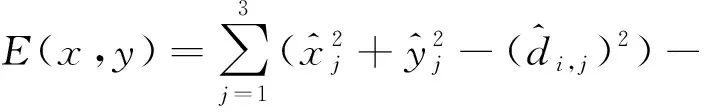
(10)

(11)

将式(11)代入式(1)，可得非约束优化问题。然后，利用BFGS算法迭代求解式(9)。求解步骤为：

步骤一，对参数进行初始化。由Bounding-box算法估计未知节点的位置，并将此位置作为X的初值；设置误差阈值ξ和最大迭代次数Nmax；将迭代次数k赋予0。

步骤三，设置步长γk，并更新Xk+1：Xk+1=Xk+γkdk。

步骤五，依据式(5)进行迭代运算，再执行k=k+1。

步骤六，判断k是否达到最大迭代次数Nmax，若达到，就结束迭代，否则跳转到第二步。图4给出了BFGS算法求解目标函数的主要流程。

图4 基于BFGS算法求解目标函数的主流程

2 性能分析

2.1 仿真环境

利用Matlab软件建立仿真平台，分析RCNL算法的定位误差。 在100 m×100 m区域内部署100～225个未知节点，10～30个锚节点。所有节点的通信半径在25～40 m变化。具体的仿真参数如表1所示。

表1 仿真参数

选择王宇鹏等[12]提出的基于稀疏傅里叶RSSI测距的低复杂RSSI定位算法(spare fourier-RSSI positioning, SFRP)和文献[13]提出的基于DV-hop的改进算法(IDV-hop)，并分析它们的归一化定位误差性能：

(12)

2.2 定位误差随锚节点数的变化情况

图5给出归一化定位误差随锚节点数的变化曲线，其中节点总数为100，通信半径为25 m，锚节点数范围为10～30。

图5 归一化定位误差随锚节点数的变化情况

由图可知，定位误差随锚节点数的增加而下降。这符合预期：网络内锚节点数越多，未知节点从锚节点获取的测距数据越多，这有利于提高测距精度。同时，锚节点数越多，锚节点分布密度也越高，这也提高了测距精度。测距精度越高，定位误差就越小。

此外，相比于SFRT和IDV-Hop算法， 提出的RCNL算法降低了平均定位误差，分别下降约2%和6%，原因在于：RCNL算法既从测距阶段和定位阶段进行了优化。通过加权正态滤波滤除了偏差大的RSSI值，提高了测距精度；结合Bounding-box法和拟牛顿迭代法定位，提高了定位精度。

2.3 定位误差随通信半径的变化情况

图6绘制了归一化定位误差随通信半径的变化情况，其中节点数为100，锚节点数为15，节点通信半径范围为15～35 m。

图6 归一化定位误差随通信半径的变化情况

从图6的曲线走势可知，增加节点的通信半径可有效地降低定位误差，定位精度得到提升。这符合预期。通信半径越大，节点间的通信跳数减少，测量RSSI的误差降低，提高了测距精度。

相比于SFRT和IDV-Hop算法，RCNL算法仍保持低的定位误差。这是因为RCNL算法先利用Bounding-box算法搜索未知节点的位置，并将此位置作为BFGS拟牛顿法的初始值进行迭代，进而对该位置进行修正，从而提高了未知节点位置的精度。

2.4 定位误差随节点数的变化情况

最后讨论未知节点数对定位误差的影响。图7给出归一化定位误差随节点数的变化情况，其中锚节点数占总节点比例为15%，节点数范围为100～225，通信半径为30 m。

图7 归一化定位误差随节点数的变化情况

从图7曲线走势可知，最初，节点数的增加使定位误差迅速下降。但当节点数增加至约160时，定位误差不再随节点数的增加而下降。原因在于：最初，尽管节点数在增加，但节点数仍较少，锚节点数在增加，这有利于增加定位精度。但当节点数增加至一定量后，相对于未知节点数的分布密度，锚节点的分布密度下降。

2.5 算法的复杂度

用算法的运行时间表征算法的复杂度。运行时间越长，算法越复杂。在联想小新Air14，系统为Windows10，处理器为Intel i5，内存容量为16 GB的PC机上运行定位算法。

实验参数：通信半径为30 m；未知节点数为150，锚节点数为30。最大的迭代次数为100。表2给出RCNL算法、SFRT和IDV-Hop算法的运行时间。从表2可知，提出的RCNL算法的运行时间高于SFRT和IDV-Hop算法。原因在于：RCNL算法执行Bounding-box算法和BFGS拟牛顿法，增加了运行时间。RCNL算法的运算时间达到45.2 s。参照文献[14]，在室外空旷地区GPS的平均定位时间约156 s。相比于GPS系统，RCNL算法的45.2 s定位时间可接受。

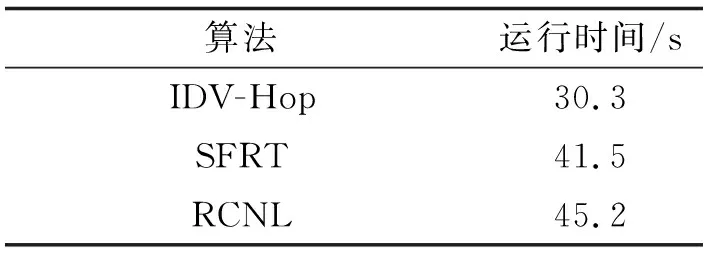
表2 算法的运行时间

综上分析可知，RCNL算法具有较高的定位精度，但其复杂度也较高，定位时间达到45.2 s。即RCNL算法以高的复杂度为代价，得到高的定位精度。高的复杂度使RCNL算法不能及时地估计节点的位置，无法适用于实时性要求高的应用场景。

3 结论

为了降低基于RSSI测距的节点定位误差，提出基于测距修正和拟牛顿法节点定位 RCNL算法。RCNL算法通过正态滤波剔除误差较大的RSSI值，提升测距精度。并利用Bounding-box算法和拟牛顿法估计节点位置，提高了定位精度。

然而，提出的RCNL算法的复杂度仍偏高，后期将进一步优化RCNL算法，在保证定位精度的同时，降低算法的复杂度，缩短定位时间，拓展RCNL算法的应用场景。