旋转式定向战斗部起爆参数研究

张 鹏，黄广炎,2，郭志威，冯顺山

(1 北京理工大学爆炸科学与技术国家重点实验室，北京 100081;2 北京理工大学重庆创新中心，重庆 401120)

0 引言

与普通战斗部相比，定向战斗部的破片毁伤场通常具有较强的方向性，对目标的毁伤效果增益较大[1-4]。旋转式定向战斗部是一种典型的定向战斗部，其采用非轴对称的定向装药结构，并利用旋转机构将装药面瞄准至目标方位，实现对目标的高效毁伤，而旋转机构的旋转时机和旋转角度，是战斗部发挥高效毁伤的关键影响因素[5-6]。

目前在定向战斗部的弹目交会方面，对定向战斗部最佳起爆延迟时间和起爆方位角的研究较多[7-11]。如郭泽荣等[7]基于六光束脉冲激光探测系统对旋转火箭弹的定向问题开展了研究，但其定向机理为弹体整体持续旋转扫描定向，与旋转式定向战斗部有较大的差异。汪金奎等[8]给出了常规战斗部破片群的飞散模型，并将破片飞散区域的边界与目标飞行区域边界相切，作为成功拦截目标的判定条件。该方法可以用来求解战斗部的最佳起爆延迟时间，但由于其考虑的是传统战斗部形式，忽略了战斗部的定向毁伤方位角，因而无法应用于旋转式定向战斗部。朱景伟等[9-10]建立了弹体-破片-目标交会模型，研究了定向战斗部弹目交会过程中战斗部最佳起爆延迟时间和起爆方位随目标速度和方位象限的变化，但模型中参与交会的破片是单个破片而非破片群，难以应用于旋转式定向战斗部非轴对称破片群定向杀伤特性的计算与评估。

以上研究的结果能够为非对称毁伤场战斗部的引战配合提供参考，但主要针对的是非旋转式定向战斗部的最佳起爆延迟时间和起爆方位角的研究，并未考虑定向杀伤破片群在弹目交会过程中对目标的作用效果。在旋转式战斗部旋转定向过程中弹目交会及引战配合的机理尚不明确的情况下，文中基于非旋转式定向战斗部的研究方法，建立了含有定向杀伤破片毁伤场的弹目交会模型，并通过仿真计算出了战斗部的最佳起爆延迟时间和最佳旋转角等引战配合参数。

1 旋转式定向战斗部弹目交会分析

如图1所示，旋转式定向战斗部通常采用非轴对称的装药方式，假定旋转式定向战斗部破片群的周向飞散角为θ，轴向飞散角为φ，在作用时，导弹先探测到目标方位，然后根据弹目交会信息驱动战斗部旋转至合适位置，使战斗部具有定向杀伤的一侧瞄准目标后起爆装药，驱动高密度破片群向目标飞散，从而实现定向杀伤的效果。

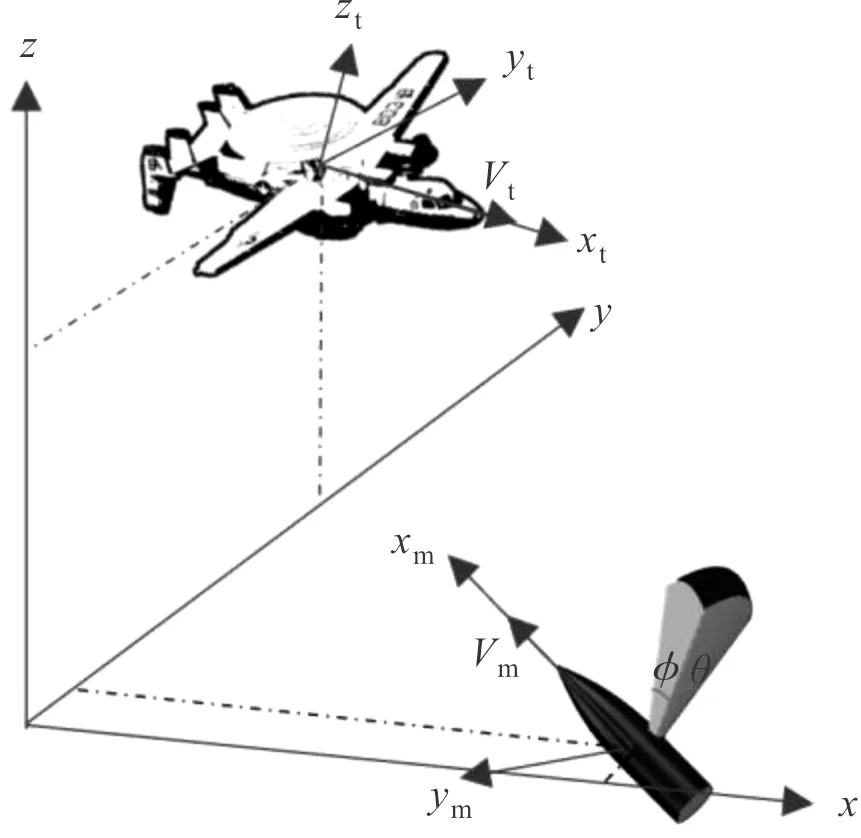
图1 旋转式非轴对称装药的定向战斗部弹目交会示意图

相对于非旋转式战斗部的弹目交会过程，旋转式定向战斗部增加了旋转定向启动时间和旋转角度两个未知量，利用现有的方法直接计算其弹目交会关键参量存在较大困难。

为此，文中建立了简化模型。假定定向战斗部中的旋转机构能在起爆前完成旋转，使定向装药结构毁伤主方向朝向目标，并且其破片群在飞散角内均匀分布，速度大小相等。在此假设基础上，将非轴对称装药定向战斗部旋转至任意角度的时间集合，等效表示为轴对称装药结构的破片飞散场，可利用其获得战斗部实现旋转定向功能后的弹目交会要求，从而简化为对旋转定向战斗部的仿真计算，如图2所示。

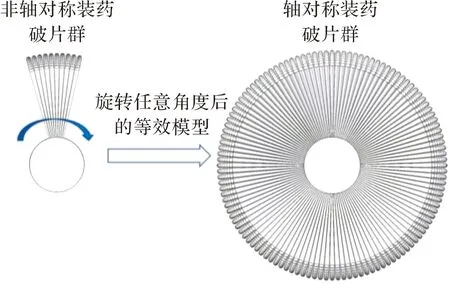
图2 非轴对称装药战斗部旋转简化示意图

采用MATLAB对弹目交会进行数值仿真，可得到弹目交会过程中导弹、目标和破片群的实时状态。轴对称装药的破片毁伤场中只有部分区域内的破片可以击中目标，结合击中目标的破片的周向方位以及对目标造成的毁伤效果等信息，可反推出旋转式非轴对称装药定向战斗部在达到最佳毁伤效果下的起爆延迟时间和旋转角。分析思路如图3所示。

图3 弹目交会参数分析过程

2 弹目交会仿真计算模型建立

2.1 基本假设

导弹和目标的遭遇时间很短，在此过程中，需对一些环境变量做出假设，以确保仿真的顺利进行。

旋转式定向战斗部与常规战斗部的区别是战斗部相对于导弹，拥有一个旋转自由度，这种特性使得旋转式定向战斗部在装载异型装药时，可主动调节破片群周向的飞散朝向，从而大大提升同等装药量下的破片毁伤率。在对其进行弹目交会研究时，因战斗部拥有一个旋转自由度，如果导弹和目标运动状态不简化处理，会使模型的仿真难度大大增加。在实际应用中，旋转式定向战斗部会在旋转定向完成后，再引爆战斗部。在弹体坐标系下，战斗部完成旋转后处于静止状态，此时引爆战斗部，破片和战斗部之间不存在牵连速度的影响。综上所述，做出以下假设：

1) 弹目交会阶段，导弹和目标的姿态和速度均不再改变。

2) 战斗部能在起爆前完成旋转定向。

3) 破片在飞行过程中受到空气阻力和重力的作用。

2.2 弹体和目标姿态参数分析

在地面坐标系下，目标在高度为H的空中飞行，导弹和目标的速度大小分别为Vm和Vt，方位分别为(xm，ym，zm)和(xt，yt，zt)，偏航角分别为γm和γt，俯仰角分别为δm和δt，滚转角分别为εm和εt。通常导弹自身的姿态信息及速度可从导弹本身携带的制导系统获取，而其携带的引信则可测得目标实时的姿态信息和速度[10]。

2.3 弹体和目标运动参数分析

在相应的坐标系下，考虑弹体和目标的运动。弹体和目标的初始速度大小分别为Vm和Vt，则两者的时间-位移方程分别为：

(1)

2.4 破片群飞散特性描述

轴对称装药的破片群是弹目交会仿真的核心部分，其构建的合理程度直接关系整个模型的计算质量。为了将破片群有机地整合到弹目交会中，首先需要获取破片群的具体分布。为方便研究，将战斗部假设为圆柱形装药、球形预制破片、中心起爆、装药长径比为2。在上述限定条件下，破片的初速大小较为一致，飞散角内的破片分布较均匀[12]。

图4 弹体坐标系下的破片群飞散模型

在弹体坐标系下讨论破片群的静态分布，破片群轴向飞散角为φ，并在周向和轴向上呈均匀分布。对破片群在周向上n等分，轴向上m等分，则破片的索引坐标可记为(i，j)，由破片的索引即可得破片在周向和轴向上的方位角。

绕x轴旋转的矩阵函数为：

(2)

绕y轴旋转的矩阵函数为：

(3)

绕z轴旋转的矩阵函数为：

(4)

设破片初始速度大小为Vs，则破片群中索引坐标为(i，j)的破片对应速度为：

(5)

式中：i∈[1，n]；j∈[1，m]。

以数组的形式存储每个破片的索引及对应的速度在x，y，z轴上的分量大小，可简化模型的计算。在得到破片的初始速度分布后，可根据质点运动原理求出破片的速度-时间和位移-时间方程。同时，破片在空气中运动，会受到重力和空气阻力的共同作用。

设破片的速度为V=[VxVyVz]T，初始速度为V0=[V0xV0yV0z]T，在Δt时间内，破片上升阶段满足的速度-时间方程为：

(6)

破片下降阶段满足的速度-时间方程为：

(7)

式中：g为当地的重力加速度，ax，ay和az是空气阻力造成的加速度在x，y，z三轴上的分量，即a=[axayaz]T。破片在飞行中受到的空气阻力与多个参数有关[13]，空气阻力加速度的表达式为a=-CρSv2g/(2m)，其中，破片迎风阻力C为常数，空气密度ρ=ρ0H(y)，破片迎风面积S=Φq2/3，ρ0为海平面处的空气密度，H(y)为距离海平面高度y公里处的空气密度修正系数，m为破片质量。

最后，对破片的速度-时间方程进行时间上的积分，即可得破片的位移-时间方程ys(i,j,t)。

2.5 坐标系转换

整个弹目交会过程的仿真需在同一个坐标系内完成，因此选择地面坐标系作为最终的参考系。破片群的模型建立在弹体坐标系上，而导弹和目标的姿态和速度均建立在地面坐标系上，故需进行坐标系的转换。转换矩阵是关于角度的函数，结合弹体和目标的姿态，可得到弹体坐标系到地面坐标系的转换矩阵为T1=Mz(2π-γm)My(2π-δm)Mx(2π-εm)，目标坐标系到地面坐标系的转换矩阵为T2=Mz(2π-γt)·My(2π-δt)Mx(2π-εt)，其中Mx，My，Mz分别为坐标轴的旋转矩阵函数[14]。

2.6 弹体-破片群-目标联合计算

在得到弹体、破片群和目标在各自坐标系下的运动状态后，设弹目交会的总时长为T，在Ts时间起爆战斗部，弹体初始位置ym0=[Lx0 0]T，目标初始位置yt0=[0LyLz]T，则t∈[0,T]时刻，地面坐标系下各单位的联合运动状态为：弹体的位移ym_g(t)=T1ym(t)+ym0；目标的位移yt_g(t)=T2yt(t)+yt0。则弹体和目标的距离为：

ymt(t)=|ym_g(t),yt_g(t)|=
|T1ym(t)+ym0,T2ym0(t)+yt0|
0≤t≤T

(8)

弹体和目标方位角为：

(9)

破片群和目标的距离为：

(10)

2.7 有效毁伤阈值

导弹拦截空中目标的过程中，当破片击中目标后，还需根据目标的易损性对毁伤效果进行进一步判别。目标易损性常因其类别不同呈现出较大差异。文中采用有效毁伤破片的数目衡量破片群对目标造成的毁伤效果。同时给出有效毁伤破片的定义：1) 击中目标要求：在地面坐标系下，如果破片和目标的距离小于L(目标长度的一半)，则认为破片击中了目标[9]；2) 击穿目标要求：击中目标的破片，其遭遇目标时的动能需大于一定的值Js[14]。

3 弹目交会特性仿真计算分析

3.1 仿真计算流程

在得到破片的初始分布后，对弹体、破片群和目标进行联合计算，实时记录下弹体破片以及目标的速度、位移等信息，同时在每一步计算中，将数据进行整理和打包，为每个破片分配独立的索引，确保其信息和索引严格对应。最终利用毁伤条件对破片进行筛选，找到有效毁伤破片，再以有效毁伤破片的数量对起爆时间和定向方位角进行筛选，以获得最佳参数。

图5 弹目交会特性仿真计算方法流程图

3.2 仿真计算输入参数

采用轴向飞散角为30°的柱形装药战斗部进行仿真计算。破片群均匀分布，破片为球形破片，初始速度V=1500 m/s，破片总数N=32400，破片质量m=0.01 kg，破片大气阻力系数C=0.97，海平面空气密度ρ0=1.25 kg/m3，500 m处的空气密度修正系数H(500)=0.9529，破片形状系数Φ=5×10-3，破片迎风面积S=5×10-5m2[14]。

导弹的初速度Vm=800 m/s，偏航角为120°，俯仰角为-30°，滚转角为0°，目标的初速度Vt=500 m/s，偏航角、俯仰角和滚转角均为0°，飞行高度500 m。在地面坐标系下，导弹的初始位置为(60 m,0 m,500 m)，目标的初始位置为(0 m,60 m,560 m)。

有效毁伤条件中，打击目标的边界条件L≤5 m(目标长度的一半)，破片击穿目标所需的动能Js=2156 J[14]。弹目交会整体的仿真时长T=100 ms，仿真步长dt=1 ms，起爆延迟时间Ts的取值范围为(0 ms,100 ms)。

3.3 计算结果分析

3.3.1 最佳起爆延迟时间Ts

战斗部在0～100 ms内起爆，仿真记录了战斗部不同的时间点起爆后，所能获得的破片群与目标最短距离，以及达到的毁伤效果，毁伤效果由有效毁伤破片的数量进行表征，如图6所示。

图6 最佳起爆延迟时间Ts求解示意图

结合打击目标的边界条件L≤5 m，曲线y1可大致描绘出战斗部起爆后破片群与目标的交会情况：在0～68 ms和84～100 ms内起爆，破片群无法打击到目标；在68～84 ms内起爆，破片群能打击到目标。故战斗部的有效起爆延迟时间范围为(68 ms,84 ms)。

再结合击穿目标动能要求Js≥2156 J，统计出有效毁伤破片数目，曲线y2可描绘出战斗部起爆后破片群对目标造成的毁伤效果：在0～68 ms和84～100 ms内起爆，有效毁伤破片的数目为0；在68～84 ms内起爆，有效毁伤破片的数量先上升，达到最大值1 369后，快速衰减为0。

最后，有效毁伤破片数量曲线最高处对应的起爆延迟时间Ts=78 ms，即为所求的最佳起爆延迟时间。

3.3.2 最佳定向角αd

破片群中破片的索引与周向和轴向方位角存在一一对应的关系。在有效起爆延迟时间范围内引爆战斗部，都会有一个扇形区域的破片群击穿目标，如图7所示。对这些破片的索引进行查询，可得到这个扇形区域的周向坐标，即有效毁伤区域的具体范围[αmin，αmax]。

图7 轴对称装药战斗部破片群周向飞散示意图

对于非轴对称装药的定向战斗部而言，意味着战斗部需要将预制破片装药面旋转到此范围内，才能达到定向毁伤效果。如图8所示，战斗部旋转使破片周向飞散区域覆盖有效毁伤区域，将破片群的中线l1和有效毁伤区域的中线l′1的夹角确定为最佳的定向角αd。

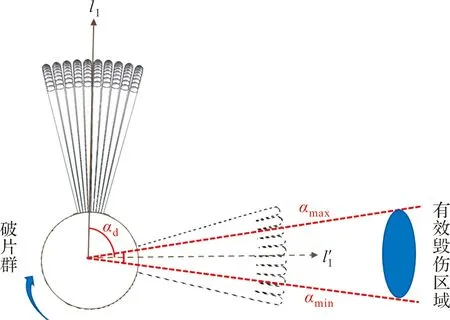
图8 定向杀伤装药战斗部有效毁伤示意图

如图9中曲线y3所示，战斗部在各个时间点起爆后，弹体坐标系下，获得的有效毁伤破片沿弹体周向上的方位角变化。在有效起爆延迟时间范围内起爆战斗部，有效毁伤破片的周向方位角存在着明显的上下界，即对应图8中有效毁伤区域的两个边界αmax和αmin。再结合有效毁伤破片数量曲线y2的最高处，得出对应的有效毁伤区域[213°，231°]，确定定向战斗部的最佳定向方位角αd=(αmax+αmin)/2=222°。

图9 最佳定位方位角αd求解示意图

3.3.3 最佳旋转角αr

定向战斗旋转至最佳定向方位角αd，需考虑目标绕战斗部的旋转和战斗部自身旋转两个过程。其中，目标绕战斗部旋转改变的是目标相对战斗部的弹目方位角，战斗部自身的旋转则是旋转机构来完成。在已求得定向方位角αd和弹目方位角αm的情况下，可反推战斗部旋转机构需要的旋转角αr=αd-αm。

图10中曲线y4表示在弹体坐标系下，战斗部在各时间点起爆时，目标沿弹体周向上的方位角变化。结合上文在有效毁伤破片数量最高处，同时也是最佳起爆延迟时间Ts处，取得的最佳定向角αd，可得定向战斗部的最佳旋转角αr=αd-αm=(αmax+αmin)/2-αm。

图10 定向战斗部旋转角αr求解示意图

(11)

如图11所示，假设定向战斗部采用的异型装药破片群静态的周向飞散角为θ，而弹目交会仿真得到的有效毁伤区域对应的破片群周向飞散角为θ′=αmax-αmin，则只需确保战斗部旋转后破片群飞散范围能将有效毁伤区域覆盖，即边线l2和l′2重合，就可取得较理想的毁伤效果。

图11 定向角αd调整示意图

由此可得：

(12)

从式(12)可以看出，当交会条件一定时，战斗部异型装药破片群的周向飞散角θ越大，所需的平均角速度越小。

4 结论

旋转式非轴对称装药定向战斗部的破片群在周向和轴向上都存在一定的飞散角，造成弹目交会过程中的旋转定向时机不确定的问题。文中提出了基于轴对称装药战斗部的飞散模型研究旋转式非轴对称装药定向战斗部关键弹目交会参数的方法，可以计算出相对应以及任意交会条件下最佳起爆延迟时间和旋转角的具体计算方法。

仿真结果表明，旋转式非轴对称装药战斗部的弹目交会过程可以依托非旋转式轴对称装药战斗部进行研究，利用建立的弹目交会模型，可以计算出对应交会条件下旋转式非轴对称装药定向战斗部达到最佳毁伤效果时的最佳起爆延迟时间、最佳定向方位角、最佳旋转角，并以此确定旋转机构旋转定向响应速度要求。

该研究方法并不局限于对旋转式非轴对称装药定向战斗部引战配合参数的求解，还可为基于非轴对称毁伤场的各类定向战斗部的设计与优化提供坚实的研究基础及方法论参考。