导弹海绵层适配器快速设计方法

李昱霖，孙立东，武秋生，李心洁，张 鹏，安庆升

(1 上海机电工程研究所，上海 201109； 2 空军装备部驻上海地区第一军事代表室，上海 200235)

0 引言

导弹尾推式发射筒具有体积小、弹射过载小、弹射速度高等优点，弹射器本身结构简洁，单车载弹量高，对导弹冲击小，是目前战术型号中推广的新技术。而尾推式弹射技术需要适配器来配合实现支撑、减振、导向[1]等作用。

当前国内外对导弹适配器的研究主要集中在掉落轨迹研究[2-3]、力学性能研究[4-5]、分离可靠性研究[6-7]等，对于适配器设计方法[8]研究较少。在适配器材料研究方面，适配器所采用的材料主要有橡胶类(如天然橡胶、丁腈橡胶、丁基橡胶、乙烯丙烯橡胶、氯丁橡胶等)、聚氨酯弹性体、聚氨酯泡沫等材料或上述几种材料的混合物。在适配器结构研究方面，主要为实心适配器的研究，空心适配器的研究主要为减振、改善受力-变形特性等[9]。因此，目前主流适配器是以聚氨酯泡沫为支撑层，海绵层为适配层结构。

在该类产品的设计过程中，设计师主要依靠经验与数值分析来完成[10]。适配器设计的具体流程为：1)根据经验预估适配器尺寸与海绵层厚度；2)数字化设计适配器，并进行有限元数值仿真；3)根据结果推算出预估的尺寸是否满足总体要求，如果不满足，根据结果修正支撑层尺寸及海绵层厚度，重复上述步骤至到满足并得到最终结果。上述方法在不计时间成本下最终能够设计出满足要求的适配器，但不一定为较优的结构。实际上，由于适配器变量较多，包括海绵层密度、厚度，支撑层高度、长度、位置分布等，除此之外，若再考虑适配器变形约束、压强约束等条件，理论上有多个满足要求的优化解。根据经验与数值分析很难得到所有尺寸都优化后的最优解。

为了解决上述问题，文中研究了海绵层适配器的一种快速设计方法。首先利用刚性梁简化导弹、非线性弹簧简化海绵层并进行参数化建模[11]；其次采用连续松弛变量处理离散变量，建立离散混合约束优化数学模型[12]；最后对拉格朗日乘子法进行改进，结合基于模糊聚类的自适应代理模型(fuzzy clustering for design space reduction, FCR)优化策略[13]将约束优化问题转为无约束优化问题进行寻优[14]。通过求解目标函数的最小值，间接获得满足所有约束条件下适配器变形一致的结构尺寸。该方法可自动探测结构的优化解，几十分钟内就能搜索出一系列满足要求的优化解，设计师仅需根据实际工程需求从中挑选出与实际工况更相似的结构尺寸进行设计，快速可靠。

1 离散混合约束优化数学模型

适配器的长度、厚度、位置分布等参数是连续变量，而海绵层的规格种类是离散变量，目前工程上主要有5种规格的海绵层，密度分别为0.43 g/cm3、0.49 g/cm3、0.55 g/cm3、0.61 g/cm3、0.64 g/cm3，对应的非线性应力应变曲线是各自独立的。因此，采用连续松弛变量方法对离散变量进行连续化处理，以便常用的试验设计方法和代理模型技术可适用于涉及混合变量的优化问题。

文献[15]提出了采用连续松弛变量代替离散变量，但该方法并不适用于非整数离散变量，为了解决该类问题，采用彭磊[12]提出的连续松弛变量法，建立连续离散混合约束优化问题数学模型：

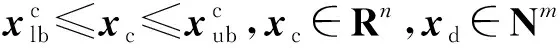
(1)

式中：xc是由n个连续设计变量组成的集合，而xd是由m个离散设计变量组成的集合。

对于理想适配器，要求在存储状态下，前、中、后3组适配器变形相同，能够使导弹存放时不发生角度倾斜，即变形相同，转化为目标函数：

F(xc,xd)=δ[(ΔU2-ΔU1)2+(ΔU3-ΔU2)2+
(ΔU1-ΔU3)2]+ω

(2)

式中：ΔU1(xc,xd),ΔU2(xc,xd),ΔU3(xc,xd)分别为存储条件下前、中、后适配器的变形，δ为放大系数，默认取值δ=10；ω为非零数值，默认取值ω=3。若优化结果满足式(2)，则表明前、中、后适配器变形相同。

设计总体要求：在一定安全系数作用力下，适配器最大变形不超过一定值，使导弹空气舵根部避免碰撞；适配器对导弹作用的压强应小于一定数值，保证导弹涂层厚度，防止涂层变薄出现由气动加热带来的问题。转化为约束条件：

(3)

式中:ΔU′1(xc,xd),ΔU′2(xc,xd),ΔU′3(xc,xd)分别为前、中、后适配器在一定安全系数作用力下的变形，默认安全系数nε=3；ΔP′1(xc,xd),ΔP′2(xc,xd),ΔP′3(xc,xd)分别为前、中、后适配器在一定安全系数作用力下产生的压强，默认安全系数np=3。

适配器设计参数包括了长度Li,宽度θi，位置分布xi，海绵层厚度hi，海绵层密度ρi等，i=1,2,3。因此，式(1)转化为适配器的数学模型：

minF(xc,xd)=δ[(ΔU2-ΔU1)2+(ΔU3-ΔU2)2+
(ΔU1-ΔU3)2]+ω
s.t.G1(xc,xd)=max(ΔU′1,ΔU′2,ΔU′3)-ε≤0
G2(xc,xd)=max(ΔP′1,ΔP′2,ΔP′3)-p≤0
xc={L1,L2,L3,θ1,θ2,θ3,x1,x2,x3,h1,h2,h3}
xd={ρ1,ρ2,ρ3}

(4)

2 导弹与海绵层参数化建模

为了求解式(4)中的ΔUi=ΔUi(xc,xd),ΔU′i=ΔU′i(xc,xd),ΔP′i=ΔP′i(xc,xd)，需要建立参数化的黑箱模型，即从(xc,xd)到它们取值的映射关系。为了减小计算分析时间，对有限元模型进行简化后，再编写脚本参数化设计。

2.1 导弹简化模型

存储状态下的导弹在重力作用下会对适配器产生压力。一般将该压力的3倍作为设计指标模拟运输过载，研究适配器的受载能力与海绵层的变形能力。相对于具有一定柔性的适配器，可以将导弹作为刚体处理。由于导弹截面大小对适配器力学性能并无影响，因此将导弹简化为刚性梁，在刚性梁上布质量点作为质心对适配器产生压力。

2.2 适配器简化模型

适配器的适配功能主要由海绵层承担，而其他结构的变形可忽略不计。因此，将海绵层的非线性材料属性简化为非线性弹簧，上下部分分别用非线性弹簧化简。非线性弹簧的力-位移曲线根据数据库中的应力-应变曲线转化后自动赋值；初始长度即为海绵层的设计厚度。

2.3 参数化流程

对简化模型进行有限元建模，其中非线性弹簧(海绵层)一端与刚性梁(导弹)固连，另一端进行固定约束。施加重力场，使导弹在质心处的质量单元产生力对非线性弹簧加压。

建好有限元模型之后，通过Python对模型参数变量进行提取，并建立黑箱模型的映射关系。连续变量可在有限元模型中直接表现出来，比如厚度h即为海绵层的厚度，h0为包装适配后海绵层厚度，均可直接作为参数输入。对于长度、宽度来说，由于模型进行了简化，无法体现，不能直接赋值。对于密度来说，影响适配器海绵层材料属性体现为海绵层的应力-应变曲线。

因此，将密度作为离散变量，不同密度一一对应相应的应力应变曲线，长度与厚度决定了适配器的接触面积S，厚度h与可允许的变形量 决定了厚度方向的变形。这样，通过自编程序，将长度、宽度、密度、厚度共同相互作用，将应力-应变曲线转化为每个适配器海绵层的力-位移曲线，自动赋值给非线性弹簧，转化流程如图1所示。

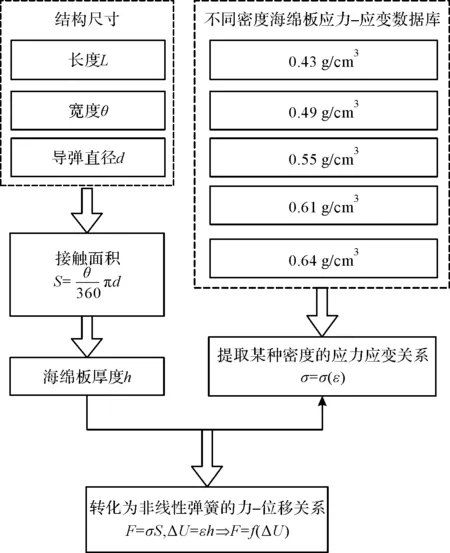
图1 应力-应变转化为力-位移曲线流程图

综上所述，以Abaqus为建模工具，利用Matlab、Python和批处理语言对导弹、海绵层进行结构参数化。参数化流程图如图2所示。输出量ΔUi，FNi分别为前(i=1)、中(i=2)、后(i=3)适配器的位移变形量与其受到的导弹自重压力。

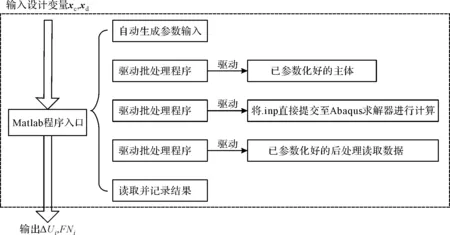
图2 参数化流程

3 约束优化策略

在工程应用中，除了目标函数以外，绝大多数的工程优化问题都会涉及约束条件。针对有限元高精度分析模型，采用文献[14]的方法对拉格朗日乘子法[15]进行改进，结合FCR优化策略将约束优化问题转为无约束优化问题进行寻优。基于拉格朗日乘子法的FCR优化策略流程图如图3所示。

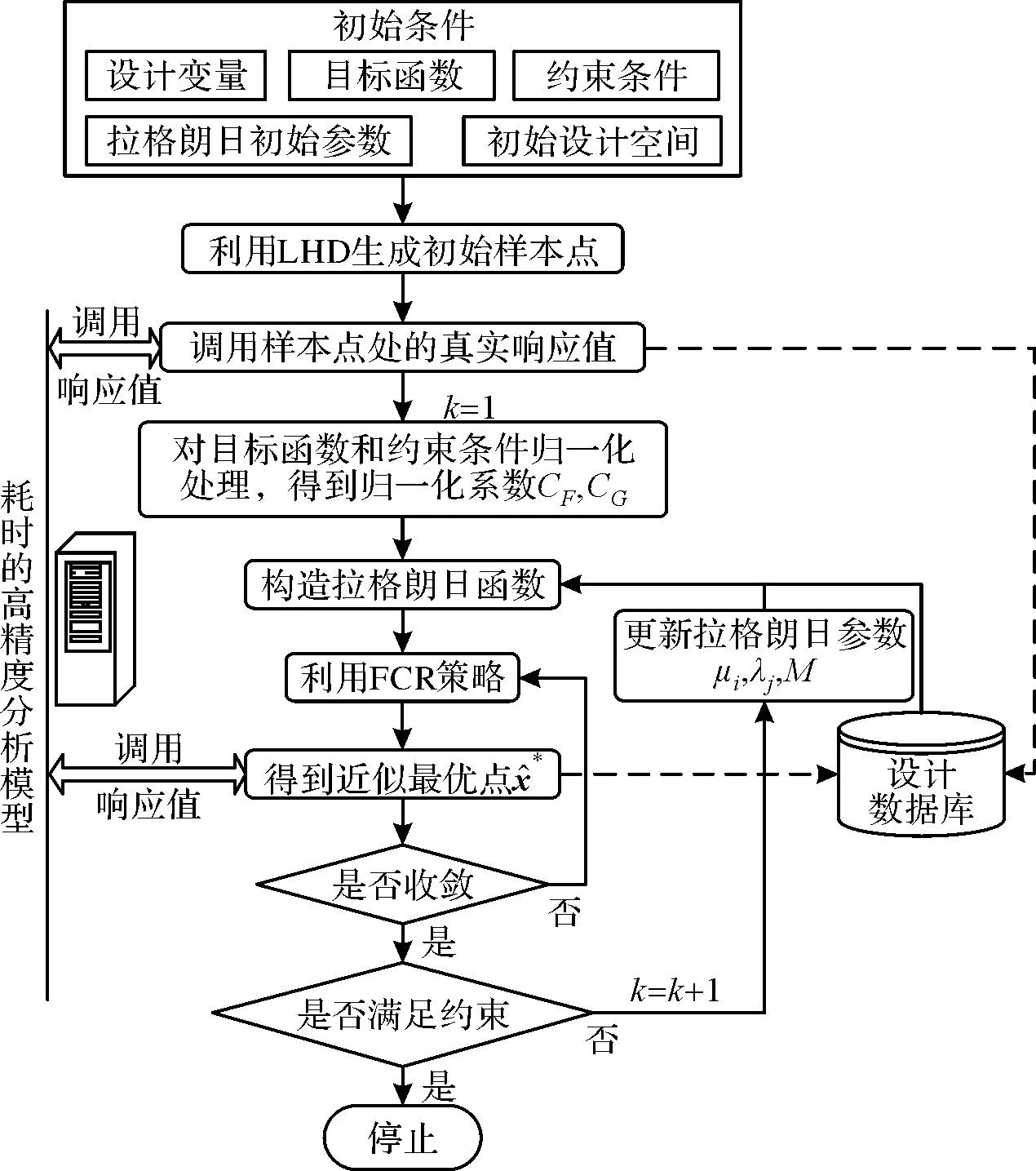
图3 基于拉格朗日乘子法的FCR优化策略

4 快速设计方法流程

以离散混合约束优化数学模型为研究对象，参数化建模为研究过程，以基于拉格朗日乘子法的FCR优化策略为研究工具，最终得到海绵层适配器的快速设计方法，共分为4个步骤：

步骤1，根据实际情况将海绵层适配器转化为设计参数，确定哪些参数已经确定，哪些参数需要设计。根据可设计参数、总体给出的最大变形与压强的指标，建立式(4)的数学模型。

步骤2，根据实际情况，初步估计这些可设计参数的取值范围。

步骤3，利用Abaqus对简化的导弹、海绵层进行有限元建模并参数化，利用自编程序封装成黑箱模型并预留输入输出接口，为优化策略提供优化对象。

步骤4，利用基于拉格朗日乘子法的FCR优化策略将约束优化转化为无约束优化，并对式(4)进行优化计算，得到最小值对应的设计变量：

(5)

这样，文中方法可将适配器设计问题转化为一个满足特定约束条件下的简单的无约束优化问题。能够快速得到最优解，并较为精确地满足总体要求。

5 快速设计方法的应用

以某型号海绵层适配器为设计实例，说明文中设计方法的快速性与准确性。

5.1 问题描述

该型号导弹需要设计前、中、后适配器来支撑直径不同的变截面导弹。即需确定前、中、后适配器分别受到的支反力压强、变形。

总体要求：

1) 导弹表面最大受压≤0.3 MPa；

2) 适配器最大变形≤2 mm。

需确定适配器长度、宽度、海绵层密度、海绵层的厚度等，除满足上述总体要求，还要确保在贮运过程中前、中、后适配器变形量相同，导弹不出现倾斜贮运。

5.2 设计流程

步骤1，根据实际情况将海绵层适配器转化为设计参数，确定哪些参数已经确定，哪些参数需要设计。

1) 总体对适配器位置进行了限定，无需自动设计位置。

2) 根据已有经验，适配器宽度直接设定为120°。

3) 中、后适配器截面尺寸相同，为了简化工艺，可限定中、后适配器完全一样。

4) 前、后适配器高度不同，但为了海绵层生产工艺，可限定海绵层厚度一样，而下部的支撑层不同。

可设计的参数精简为：前适配器长度L1；中或后适配器长度L2；前、中、后海绵层厚度h；前海绵层密度ρ1；中或后海绵层密度ρ2。

步骤2，根据实际情况，初步估计可设计参数的取值范围。

对于海绵层厚度，若不提前进行预估，优化过程不但耗时，而且优化后得到的厚度尺寸存在无法制造的风险。在制造工艺方面，海绵层在7～15 mm厚度下密度精度控制较好，过薄或过厚海绵层密度精度将会大幅下降。因此，首先限定海绵层厚度h的设计范围为7～15 mm。

对于适配器长度，总体给的接口是前适配器小于300 mm，中或后适配器小于130 mm。为了避免失稳，长度方向不能太短。因此，估计L1为180～300 mm，L2为65～130 mm。

对于密度，前、中和后适配器自动从5种不同密度的海绵层选取。

步骤3，利用Abaqus对简化的导弹、海绵层进行有限元建模并参数化。

需要注意的是，由于指标给出了最大变形小于2 mm。则代表海绵层初始压缩量至少为2 mm，这样海绵层变形后不会与导弹接触面产生间隙，失去适配功能。因此，除了必须参数化的设计参数外，还需参数化非线性弹簧的外部接触位置，即海绵层厚度(h-2)mm作为非线性弹簧非导弹接触侧的位置。

步骤4，利用基于拉格朗日乘子法的FCR优化策略将约束优化转化为无约束优化，约束优化模型为：

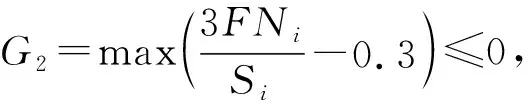
(6)

利用FCR策略进行优化，共调用有限元模型87次，最终变量优化结果如表1所示。

表1 优化计算结果

Y为通过10倍放大后的倾斜方差，其值仅为3.008 8 mm2，说明了在导弹自重下前、中、后适配器几乎不会倾斜。G1、G2为负数表明了其能够满足总体要求，即3倍过载下最大变形小于2 mm，最大压强小于0.3 MPa。每次调用分析模型大约耗时15 s，调用87次仅需约20 min就能找到优化结果，使得设计师快速找到设计参考值。

5.3 工程设计

根据工程误差及设计经验，通过设计参考值，设计出适配器海绵层厚度7 mm，海绵层取密度为0.55 g/cm3的成熟产品，前适配器长243 mm，中、后适配器长84 mm。设计后的适配器如图4、图5所示。

图4 中、后适配器实物

图5 前适配器装入筒弹后的状态

所设计生产的适配器顺利通过了运输考核，并且适配器的设计与生产一次性完成，说明了文中海绵橡胶适配器快速设计方法的正确性。

若采用传统的设计方法，需要凭经验预估一个大致的尺寸，且直接指定密度、长度等参数，无法进行优化设计。在时间成本上，首先，仅进行有限元建模仿真就需约1 d时间。若经验不足，估计的结构尺寸不准确，还要重复返工。其次，方案设计中，总体要求可能会随时改变适配器位置、接口等，传统方法还不能快速跟进总体要求，往往是造成型号进度拖后的重要原因。而文中快速设计方法能够在不到半小时时间里快速得到准确的优化结果，具有快速高效的优势。

6 结论

文中提出的海绵层适配器的设计方法能够快速找到设计参考值，并根据总体要求以及实际产品状况，快速设计出海绵层适配器各种参数，为设计师提供一种快速设计方法，在半小时内得到有效反馈参数，大大提高了设计效率，节约了人力成本，不但能够搭建一个快速设计平台，而且对海绵层适配器提供了一种通用设计方法。